随着社会经济的发展和生活水平的提高,人们对汽车的需求量逐年大幅度上涨,环境问题也随之而来,汽车尾气的排放对环境造成极其严重的影响。面对严峻的环境问题,我国大力推动碳达峰、碳中和各项工作,电动汽车产业普及率不断提升[1]。电动汽车一方面满足人们的短距离出行需求,另一方面它以电作为主要动力源,相比以燃油为驱动的汽车更加节能和环保。目前对于路径规划的研究主要针对燃油汽车,而对燃油汽车的路径规划无须考虑电量的因素,该场景不适用于电动汽车。随着电动汽车的普及,由于电动汽车的特殊属性以及“里程焦虑”[2],电动汽车的出行规划显得尤为重要。若能有效引导电动汽车用户选择可达目的地、能及时充电、行驶时间短、充电时间短的路线行走,出行效率就能有效提高。
本文提出了一种基于逆强化学习(Inverse Reinforcement Learning,IRL)的电动汽车出行规划(Electric Vehicle Travel Planning, EVTP)方法,将考虑充电行为的Dijkstra算法作为专家示例以保证专家策略的优越性,在对电动汽车进行出行规划时须同时考虑电量和路径两方面因素,从而得到一条满足电量可达条件的最优路径。此外,本文还对充电策略进行考虑,在充电时采用部分充电策略以提高充电效率,使充电时间尽可能短。逆强化学习算法旨在对寻找路径的策略进行学习,因此有别于传统路径规划算法依赖于路网结构的特性。
1 相关工作电动汽车出行规划(EVTP)问题可以拆分为电动汽车路径规划问题(Electric Vehicle Routing Problem, EVRP)以及充电策略问题。电动汽车的路径规划问题会受到电动汽车电池容量的限制,即电动汽车的电量不能低于某个限定最小值。因此,EVRP也可以被建模为受约束的最短路径规划问题,此类问题与经典的最短路径问题的不同之处在于解决方案必须满足附加约束,这是典型的NP-hard问题[3]。目前,求解受约束的最短路径问题大体上可分为两类方法:精确方法和启发式方法。
精确方法通过严谨的数学模型或数据结构规划问题,利用数学法则或数据结构搜寻的方式求得问题最优解[4]。Lu等[5]提出了一种运用整数线性规划来求解电动汽车最优路线问题的方法,该方法以最小化电动汽车行驶时间为优化目标,然而线性规划的方法计算复杂度较高,仅在小型实例中有很好的表现,一旦应用在大型路网中往往需要很大的存储空间而导致方法不可用,因而其效率取决于实际路网的规模且不可直接迁移到其他未经预处理的路网中。
由于精确方法有较高的计算复杂度而不便应用于实际情况,在此方面有一定改善的启发式方法是EVRP中更为常用的一种求解方法。启发式方法[4]的主要思想是以当前解为基点,在当前解的邻域中寻找较优解赋给当前解,并继续寻找,直到没有更优解为止。Lebeau等[6]对每条路径计算合并一条新路径的成本,对可行路径按成本量排序,再以贪心方式进行归并得到路径集。Felipe等[7]采用两阶段启发法,在得到初始可行解的基础上不断对路径进行调整,以逐渐靠近最优目标,并在每一步更新目标函数的值,反复迭代直到目标函数的值收敛为止。类似地,Dijkstra算法和A*算法[8]在路径规划问题中也被广泛运用,对其稍加修改也可以运用到EVRP中。Cuchý等[3]提出了一种基于A*算法计算电动汽车最优路线的方法,并将减少充电行为中的等待时间作为优化的一部分。Kobayashi等[9]提出了一种基于Dijkstra算法的电动汽车路线搜索方法,这种方法对于充电行为也有一定的考虑,但未对充电时间作出优化。虽然启发式方法能有效减少运行时间,但是此类方法仍然不能独立于实际路网,即其运行效率仍与路网规模相关,且应用在不同路网时需要重新进行生成邻接矩阵等数据预处理工作。而本文提出的基于逆强化学习的方法与具体路网结构无关,即在某个路网中训练得到的模型也能在其他路网中有较优的性能。
对于EVTP问题,为得到一条最优路径,除了路径最短之外,充电策略也是需要重点考虑的因素。Wang等[10]提出了一个基于电量驱动的上下文感知路径规划框架,该算法通过电量的约束限制A*算法对路径进行搜索,并且对于需要充电而绕路的情况给出了最佳方案。然而,此类方法在到达充电站时仍假设电动汽车会将电量充满,这并不适用于实际情况。在现实生活中,电动汽车通常只需要使其电量在接下来的路程中不会低于限定值即可,这样既可以减少充电时间又能满足可达性。此外,电动汽车的充电函数并不是线性的,电动汽车的充电效率会随着电量的变化而变化[11]。因此,本文提出了一种更接近于真实情况的充电策略,即分段充电以及部分充电策略。
2 方法 2.1 问题定义对于EVTP问题,电动汽车车主通常希望得到一条行驶时间短、充电时间短、充电次数少的可达路径。因此,目标可形式化表达为
| $ \min \sum_{i, j:(i, j) \in E} \frac{d_{i j}}{-v} x_{i j}+\sum_{j \in C}\left(s_j+c_j\right) y_j $ | (1) |
式中,E表示路网中边的集合;dij表示路径(i, j)的距离,v表示电动汽车在一条路径中的平均速度,则
此外,在寻找路径的过程中还应满足以下条件:(1)电动汽车选择的每一个节点都在路网的点集G中,选择行走的每一条路径都在边集E中;(2)路网中的边为无向图,选择边(i, j)等价于选择边(j, i),即xij=xji;(3)选择的任意两个连续的充电桩之间的电量消耗要小于限制条件,即到达充电桩时的电量大于限定的最小电量;(4)充电次数尽可能少。充电次数越多,充电桩总计服务时间越长[12],从而会降低电动汽车的出行效率。
2.2 马尔可夫决策过程为将逆强化学习(IRL)算法应用到EVTP问题中,EVTP问题可被建模为马尔可夫决策过程[13, 14]。在此场景中的马尔可夫决策过程可由以下5元组表示。
(1) 状态集S。在EVTP问题中,状态集S中的每一个状态s由当前电动汽车的电量(pow)、与终点的距离比例(distance_ratio)、行走的角度(degree)、绕路情况(loop)组成。通过pow可以判断当前状态是否满足可达性条件,即行走时电动汽车的电量是否在限定值以上。另外,状态值的其他组成部分也是电动汽车选择路径过程中需要特别关注的因素,状态值中不包含具体位置信息,使得训练得到的模型在新的路网中也能有较好的表现。
(2) 动作集A。由于电动汽车的特性,动作集A中的动作a包含两类:行走行为和充电行为。在本文的设定中,动作集中共包含10个动作,前8个动作表示行走行为(假设所有的节点最多有4个邻接节点),后2个动作表示充电行为,集中离散化的动作用one-hot编码[15]表示。在行走行为中,电动汽车的目标是向更接近终点的方向行驶,且需要为之后可能出现的充电行为做准备。因此,行走行为中的前4个动作对某一位置的相邻点按照(degree, distance_ratio)升序排列,即先按照degree升序排列,若degree相同再按照distance_ratio升序排列;行走行为中的后4个动作对某一位置的相邻充电站按照上述规则排序,以便之后选择充电行为。若选择动作集中后2个动作,即电动汽车选择充电行为,在充电行为中本文对于充电量进行了区分,其中一个动作表示电量充到80%,而另一个动作表示电量充到100%,这种部分充电的策略有利于节省充电时间。
(3) 奖励r。传统强化学习算法中的即时奖励r往往是人为设定的,然而在复杂问题中仅凭经验通常无法设置最优的奖励值。例如,本文的场景需要同时考虑行走行为以及充电行为,难以人为设置兼顾二者的最优奖励。奖励是影响强化学习算法性能的重要因素,因此,本文采用基于逆强化学习的方法对奖励值进行设定[16],通过专家示例以及学习策略过程中得到的轨迹间的交互,求得最优的奖励值。
(4) 动作价值Q。Q(s, a)表示选择了动作a之后直到到达终点的奖励总和的期望,即
| $\begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;Q(s, a)=E\left[\sum_{t=0}^T \gamma^t r\left(s_t, a_t\right) \mid s=s_0, a=\right.\\ \left.a_0\right]。\end{array} $ |
本文用Dueling DQN算法[17]近似动作价值Q,即将某一时刻的状态st作为输入,输出对每个动作a的价值预测。此时Q值被定义为Q(s, a; θ),其中θ为神经网络中的参数。
(5) 策略π。策略π(st)依据当前状态对动作进行选择。在本文中使用ε-greedy以一定的概率进行探索,即大概率选择动作价值最大的动作,以极小的概率对动作进行随机选择来避免陷入局部最优。ε-greedy的计算公式如下:
| $ \begin{gathered} \pi\left(s_t\right)= \\ \left\{\begin{array}{l} \arg \max _{a \in A} Q(s, a) \text {, if } \operatorname{random}[0, 1]>\varepsilon \\ \text { random } a \in A, \text { otherwise } \end{array}\right.。\end{gathered} $ |
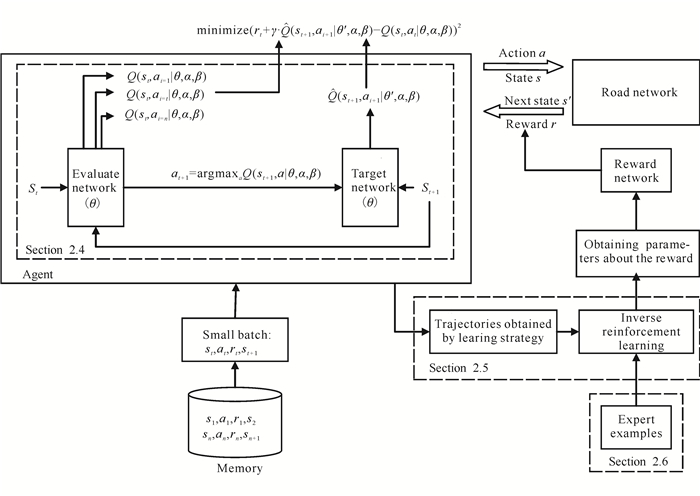
根据上述5元组,对算法整体流程表示如图 1所示。
|
| 图 1 算法整体流程图 Fig. 1 Overall flow chart of algorithm |
2.3 状态特征选择
状态是马尔可夫决策过程中的重要组成部分,状态的选择尤为重要。特征是状态到真实值的映射,包含一些重要的属性,且与奖励值有密切关系。在本文中将EVTP问题的特征定义为5个方面。
(1) 电量pow。pow表示电动汽车是否迫切需要充电。此特征用当前状态下电动汽车的剩余电量来定义,剩余电量越少越迫切需要充电。
| $ f_{\text {pow }}\left(s_t\right)=\operatorname{Soc}_t 。$ |
(2) 充电时间charge_time。充电时间是电动汽车需要重点考虑的特征之一。充电时间过长会导致旅程时间过长,从而导致效率过低;充电时间过短可能会使电量不能满足接下来旅程的需要,从而导致目的地不可达。电动汽车的充电时间需要在满足可达的条件下尽可能短。
| $ \begin{align} & \ \ \ \ \ \ \ {{f}_{\text{charg}{{\text{e}}_{\text{t}}}\text{ime}}}\left( {{s}_{t}} \right)= \\ & \left\{ \begin{array}{*{35}{l}} {{c}_{t}}\text{, if location }(t)\in C \;\text{and charg}{{\text{e}}{\text{_index}}}({t})\text{=1} \\ 0\text{, otherwise } \\ \end{array} \right. ,\\ \end{align} $ |
式中,C表示充电桩节点的集合;location(t)表示t步所在位置,location(t)∈C即t步时所在节点为充电桩节点;charge_index表示充电指示,由t步时选择的动作决定,charge_index(t)=1即表示在t步时需要充电;ct表示计算得到的在t步时的充电时间。
(3) 角度degree。degree表示当前状态所在位置与终点的连线以及起点与终点的连线之间的夹角,夹角越小说明电动汽车行驶的方向与终点方向越接近。
| $ \begin{align} & \ \ \ \ \ \ \ {{f}_{\text{degree }}}\left( {{s}_{t}} \right)=\mid \text{getdegree}(\text{origin}, \text{destination})- \\ & \text{getdegree}(\text{location}(t), \text{destination})\mid , \\ \end{align} $ |
| $ f_{\text {degree }}\left(s_t\right)=\min \left(f_{\text {degree }}\left(s_t\right), 360-f_{\text {degree }}\left(s_t\right)\right) \text {, } $ |
式中,getdegree表示得到两点之间方位角的函数;origin表示路径的起点;destination表示路径的终点。
(4) 距离比例distance_ratio。distance_ratio表示当前所在位置与终点的距离以及起点与终点的距离之间的比例关系,比例越小则越接近终点,所有距离均用haversine公式[18]进行计算:
| $ \begin{align} & \ \ \ \ \ \ \ {{f}_{\text{distanc}{{\text{e}}_{\text{r}}}\text{atio}}}\left( {{s}_{t}} \right)= \\ & \frac{\text{ haversine( location }(t)\text{, destination) }}{\text{ haversine( origin, destination) }}, \\ \end{align} $ |
式中,haversine (A, B)表示点A与点B之间的haversine距离。
(5) 绕路loop。loop表示寻找某起点终点对的路径过程中是否重复访问某一位置。
| $ f_{\text {loop }}\left(s_t\right)=\left\{\begin{array}{l} 1, \text { if location }(t) \in \text { runway_history } \\ 0, \text { otherwise } \end{array}\right.,$ |
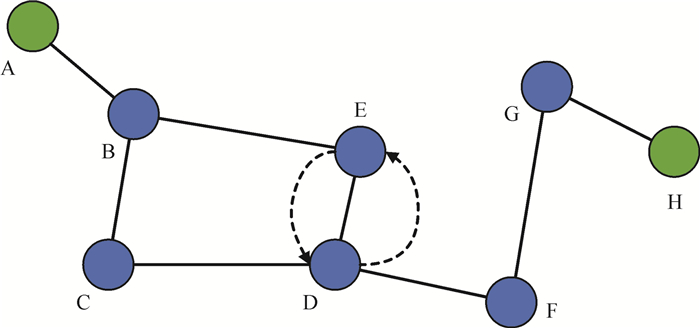
式中,runway_history表示电动汽车走过的节点位置的集合,若当前位置已经在runway_history中,则说明电动汽车已经访问过该节点,即出现了绕路。若出现绕路往往说明某步的决策不是最优,因此并不希望路径中出现绕路的情况。绕路情况如图 2所示。
|
| 图 2 绕路情况 Fig. 2 Situation of loop |
给定起点、终点对(A, H),电动汽车由E到达D后,在D点若根据角度选择下一个点,极有可能选择点E,此时便出现了绕路,虚线表示可能出现的绕路情况。
在上述特征中,电量对逆强化学习算法得到的奖励产生正向影响,充电时间、角度、距离比例、绕路均对奖励产生负向影响。
在对特征进行选择时,路径因素以及充电因素都需要被考虑以适用于EVTP问题,从而得到一条兼顾行驶和充电的最优路径。
2.4 Dueling DQN除了对特征的选择外,对动作的选择在逆强化学习中也十分重要。逆强化学习算法与传统强化学习算法的区别仅在于奖励函数,虽然其算法流程与传统强化学习相似,但是在得到奖励函数之后仍需要正向训练更新Q值来学习策略。可用Q(s, a)近似累计奖励,即
| $ \begin{aligned} & Q(s, a)=E\left[r_t+\gamma \cdot r_{t+1}+\gamma^2 \cdot r_{t+2}+\cdots \mid s_t=s, \right.\\ \left.a_t=a, \mu\right] \text { 。} \end{aligned} $ |
根据上述设定,需要求得最优动作值Q*,最优动作值函数基于贝尔曼方程[19],表示如下:
| $ \begin{align} & \ \ \ \ \ \ \ {{Q}^{*}}(s, a)={{E}_{{{s}^{\prime }}}}\left[ r+\gamma \cdot {{\max }_{{{a}^{\prime }}}}{{Q}^{*}}\left( {{s}^{\prime }}, \right. \right. \\ & \left. \left. {{a}^{\prime }} \right)\mid s, a \right]。\\ \end{align} $ |
为得到最优解,引入Dueling DQN算法,该算法是DQN算法的改进形式,采用非线性表示形式逼近动作值函数。与DQN方法类似[20, 21],Dueling DQN算法[22]用到了两个神经网络,分别表示为Q(s, a; θ)和
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;L_i\left(\theta_i\right)=E_{s, a, r, s^{\prime}}\left[\left(r+\gamma \cdot \hat{Q}\left(s, \operatorname{argmax}_{a^{\prime}} Q\left(s^{\prime}, \right.\right.\right.\right. \\ \left.\left.\left.\left.a^{\prime} ; \theta_i\right) ; \theta_i^{\prime}\right)-Q\left(s, a ; \theta_i\right)\right)^2\right] 。\end{array} $ |
在实际问题中,有时采取的动作对下一个状态的变化情况没有太大的影响,因此使用Dueling DQN算法可以提升学习效果,加速收敛。该算法将每个动作的Q值拆分成价值函数V以及每个动作的优势函数A,因此Q值可改写
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;Q\left(s, a ; \theta_i\right) =Q\left(s, a ; \theta_i, \alpha, \beta\right)=V\left(s ; \theta_i, \alpha\right)+\\ \left(A\left(s, a ; \theta_i, \beta\right)-\frac{1}{|A|} \sum_{a^{\prime}} A\left(s, a^{\prime} ; \theta_i, \beta\right)\right), \end{array} $ |
式中,α和β分别为价值函数和优势函数的参数。
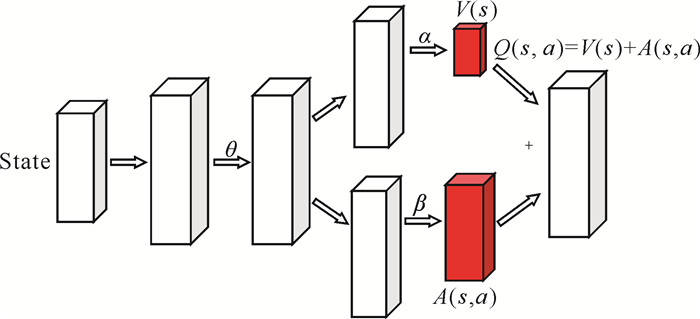
在普通DQN算法中,若想更新某个动作的Q值会直接更新Q网络,使得该动作的Q值改变。然而在Dueling DQN算法中,由于所有动作的优势函数A值的和为0,不便于对优势函数进行更新,因此Q网络将优先对价值函数进行更新,即相当于对所有动作的Q值均进行更新,从而提升学习效果。Dueling DQN的网络结构如图 3所示。在得到所有动作的Q值后,ε-greedy可被应用于动作的选择中。
|
| 图 3 Dueling DQN的网络结构 Fig. 3 Network architecture of Dueling DQN |
2.5 逆强化学习
在马尔可夫决策过程中,除状态和动作外,奖励也尤为重要。无论是传统强化学习还是逆强化学习,最基本的假设都是最大化累积的奖励,因此奖励的设计非常关键。传统强化学习的即时奖励通常凭借经验人为设定,然而像电动汽车出行规划等复杂问题,仅凭经验设置奖励往往难以精准量化,因此,逆强化学习算法应运而生。本文将逆强化学习方法应用到电动汽车出行规划中以得到最优的奖励函数。
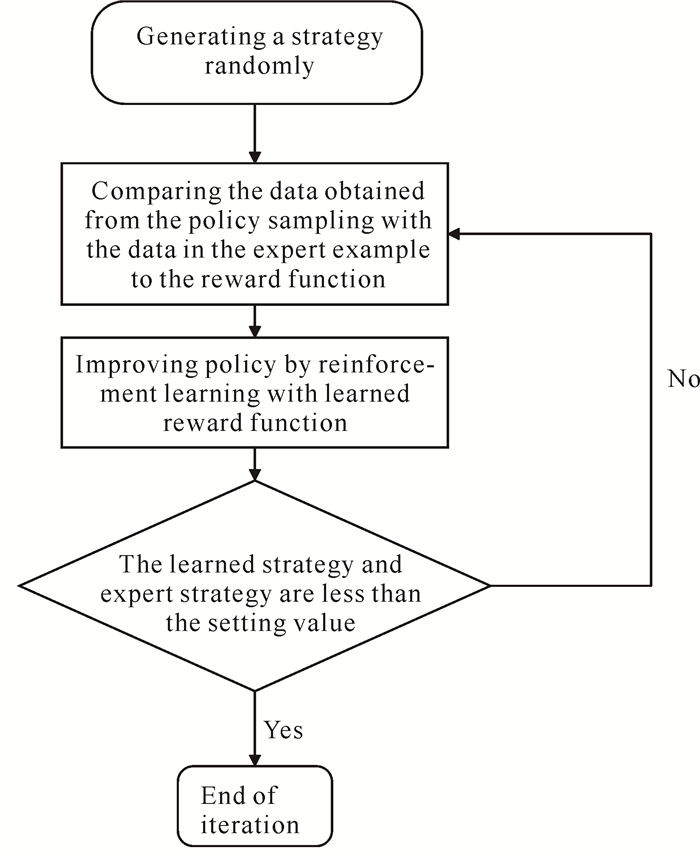
逆强化学习的思想与模仿学习有一定的相似之处,均需要借助专家示例库对问题进行优化。行为克隆是最早的模仿学习形式,与行为克隆简单学习一个状态到动作的映射不同,逆强化学习算法中奖励函数的学习方法原理如下:假设专家策略本身是根据某种奖励学到的最优策略,那么专家示例即可取得最优奖励值。根据此假设,设置参数化的奖励函数,并且寻找参数使得专家示例的奖励优于其他任意数据,这样即可求解出奖励函数。然而,上述“其他任意数据”并不具备可操作性,因此常采用迭代过程:根据当下学到的奖励函数学习策略并生成轨迹数据,该轨迹数据替代“其他任意数据”,对比专家示例和生成的轨迹数据,来学习下一轮奖励函数。逆强化学习的流程如图 4所示。
|
| 图 4 逆强化学习流程图 Fig. 4 Flow chart of inverse reinforcement learning |
奖励被定义为线性结构,即特征向量的加权和,表示如下:
| $ r\left(s_t\right)=\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{f}\left(s_t\right), $ |
式中,θ=[θ1, θ2, …, θK]为K维权值向量,K为特征向量维度;f(st)=[f1(st), f2(st), …, fK(st)]为根据状态定义的与奖励相关的特征向量。因此,一条轨迹ζ的奖励可以表示为
| $ R(\zeta)=\sum_t r\left(s_t\right)=\boldsymbol{\theta}^{\mathrm{T}} \boldsymbol{f}_\zeta=\boldsymbol{\theta}^{\mathrm{T}} \sum_{s_t \in \zeta} \boldsymbol{f}\left(s_t\right), $ |
给定Dijkstra算法得到的专家示例集D={ζ1, ζ2, ζ3, …, ζM},其中M为专家示例轨迹的数目,问题转化为找到参数θ使得专家示例的奖励最优。因此,目标函数如下:
| $ \max J=\max (R-\widetilde{R}), $ |
式中,R表示专家示例集获得的奖励,
由上述奖励函数的表示方式,目标函数转化为
| $ \begin{gathered} \max\nolimits _{\boldsymbol{\theta}} J(\boldsymbol{\theta})=\max \nolimits\left(\frac{1}{M} \boldsymbol{\theta}^{\mathrm{T}} \sum\nolimits_{\zeta_i \in D}^M \boldsymbol{f}_{\zeta_i}-\frac{1}{N} \boldsymbol{\theta}^{\mathrm{T}} \cdot\right. \\ \left.\sum\nolimits_{\tilde{\zeta}_j}^N \boldsymbol{f}_{\tilde{\zeta}_j}\right)=\max\nolimits \boldsymbol{\theta}^{\mathrm{T}}\left(\frac{1}{M} \sum\nolimits_{\zeta_i \in D}^M \boldsymbol{f}_{\zeta_i}-\frac{1}{N} \sum\nolimits_{\tilde{\zeta}_j \in \tilde{D}}^N \boldsymbol{f}_{\tilde{\zeta}_j}\right), \end{gathered} $ |
式中,N表示生成的轨迹数据集
| $ \nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta})=\frac{1}{M} \sum_{\zeta_i \in D}^M \boldsymbol{f}_{\zeta_i}-\frac{1}{N} \sum_{\tilde{\zeta}_j}^N \boldsymbol{f}_{\tilde{\zeta}_j} 。$ |
奖励函数参数θ的更新使用了梯度上升的方法,直到其收敛。为防止过拟合,本文引入了参数θ的L2正则化,目标函数改写为
| $ J(\boldsymbol{\theta})=\boldsymbol{\theta}^{\mathrm{T}}\left(\frac{1}{M} \sum_{\zeta_i \in D}^M \boldsymbol{f}_{\zeta_i}-\frac{1}{N} \sum_{\tilde{\zeta}_j \in \tilde{D}}^N \boldsymbol{f}_{\tilde{\zeta}_j}\right)-\lambda \boldsymbol{\theta}^2, $ |
式中,λ为正则化参数,且满足λ>0。
因此,梯度公式变为两轨迹集间特征期望的差异加上正则化项的梯度:
| $ \nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta})=\frac{1}{M} \sum_{\zeta_i \in D}^M \boldsymbol{f}_{\zeta_i}-\frac{1}{N} \sum_{\tilde{\zeta}_j}^N \boldsymbol{f}_{\tilde{\zeta}_j}-2 \lambda \boldsymbol{\theta}, $ |
参数θ的更新公式为
| $ \boldsymbol{\theta}=\boldsymbol{\theta}+\alpha \nabla_{\boldsymbol{\theta}} J(\boldsymbol{\theta}), $ |
式中,α表示学习率。
经过上述过程的迭代,即可求得最优参数θ,从而得到最优的奖励函数。然而,上述算法如果被运用,还需要得到专家示例库,才可通过与专家策略进行对比求得奖励函数的参数。
2.6 构建IRL专家示例在逆强化学习中,专家示例的选择会直接影响策略的学习,因此,如何构建专家示例十分关键。Dijkstra算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径的问题,在路径规划问题中得到了广泛的应用[23, 24]。考虑到Dijkstra算法能生成最短路径的特点,本文将Dijkstra算法生成的路径设置为专家示例。然而,传统的Dijkstra算法只考虑最短路径的问题,而无法同时考虑选择充电点以及计算充电时间等充电相关动作,因此需要在传统Dijkstra算法上做出一定改进。在本文中,给定起点、终点对,需要先利用传统Dijkstra算法得到最短路径,再考虑该条最短路径有哪些点在充电桩节点的集合中,由这些点作为分割点得到子路径Sub_path。对于每条子路径Sub_pathi的耗电量情况进行分析,充电指示charge_index取值如下:
| $ \;\;\;\;\;\;\;\text{charge_index} =\\ \left\{\begin{array}{l}\left.1, \text { if use_power(Sub_path}_i\right)>\text { Soc }_{i-1}-\text { limit}_{\text {batt }} \\ 0, \text { otherwise }\end{array}\right., $ |
式中,use_power(Sub_pathi)表示子路径Sub_pathi的耗电量;Soci-1表示电动汽车在最短路径中第i-1个充电桩节点时的剩余电量;limitbatt表示电动汽车的最低电量,本文设定limitbatt=0.1。charge_index=1时表示需要充电,即对于某一个路径中的充电桩节点,若下一条子路径耗电量大于剩余电量与最低电量之间的差值,则在该充电桩节点需要充电。
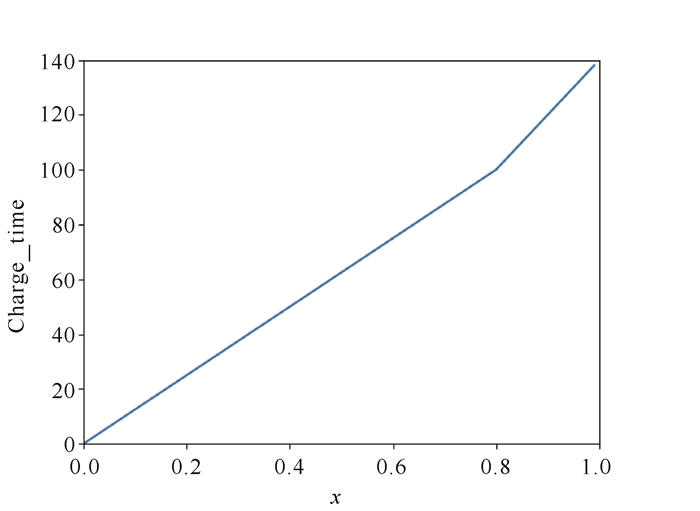
对于充电的目标电量,本文采取部分充电的策略[25]:若下一条子路径的耗电量小于等于0.7,则在此充电桩将电量充到0.8;若下一条子路径的耗电量大于0.7,则此次充电需要将电量充到1。此外,为了更接近现实中的情况,本文也考虑了分段充电的策略,从电量0充到目标电量x的充电时间charge_time如下:
| $ \begin{gathered} \text { charge_time } =\\ \left\{\begin{array}{l} \frac{x}{0.8 \times 0.01}, x<0.8 \\ \frac{x-0.8}{0.5 \times 0.01}+\frac{0.8}{0.8 \times 0.01}, 0.8 \leqslant x \leqslant 1 \end{array}\right., \end{gathered} $ |
式中,电动汽车的电量达到0.8之前的充电效率高于其电量达到0.8之后的充电效率,这与现实中的设定相同。为简化运算,本文将电量达到0.8之后所需的充电时间也用线性函数表示。关于电量的充电时间函数如图 5所示。
|
| 图 5 充电时间函数 Fig. 5 Function of charging time |
因此,一条包含充电策略的最短路径可被求得,并将此路径作为专家示例。Dijkstra算法在较小的路网中有较好的性能,然而当其运用在大型路网中,该算法需要花费很长的时间得到邻接矩阵,且它的运行效率与路网规模成正比。而本文基于逆强化学习的方法是在专家示例中学习其行走与充电的策略,这种策略对于不同的路网或大型路网也同样适用,而无需对模型重新进行训练。
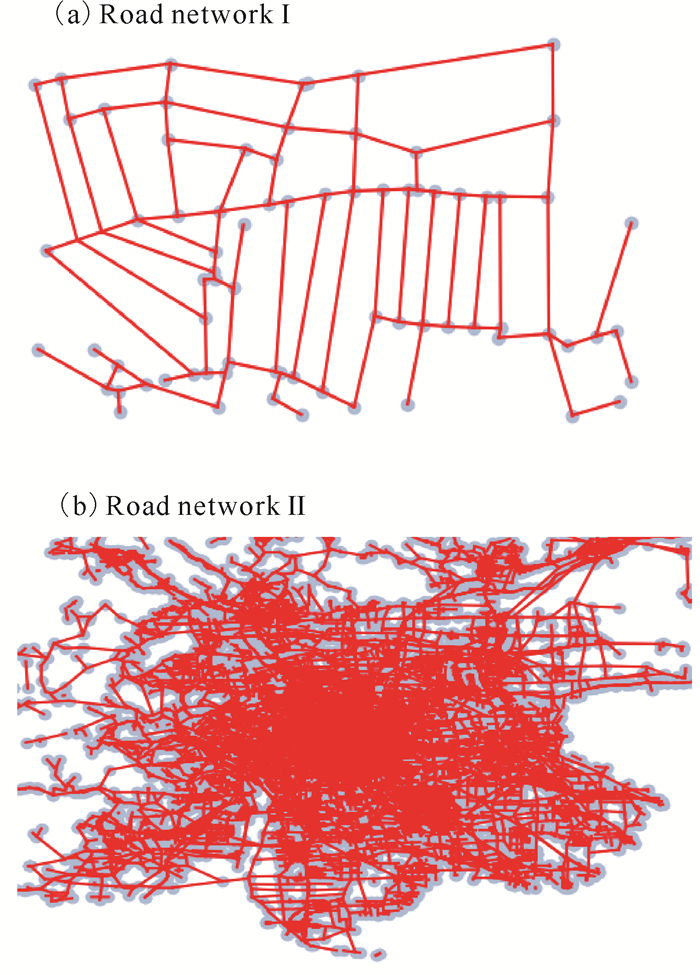
3 实验验证 3.1 数据集选用两个路网分别对模型进行训练,两个路网均是北京市路网中的一部分。路网Ⅰ包含76个节点以及105条边,纬度为39.893°-39.898° N,经度为116.390°-116.405° E。路网Ⅱ包含75 956个节点以及101 052条边,纬度为39.4°-40.4° N,经度为115.8°-117.0° E。路网的数据集由两部分构成:点集与边集,其中点集中包含各点的经纬度信息,边集中包含每条路径起点、终点的经纬度以及起点、终点之间的距离,由点集与边集构成的路网如图 6所示。由于充电桩节点的数据集未公开,且关于充电桩的布局不是本文的研究重点,因此随机选择点集中的点作为充电桩,这对实验结果并不影响。
|
| 图 6 北京市部分路网 Fig. 6 Part of road network in Beijing |
3.2 基准方法
通过将所提出的方法与以下基准方法进行比较,开展性能验证。
(1) Dijkstra & 完全充电策略(Dijkstra & Full charge)。Dijkstra算法在小型路网中能够高效地得到最短路径,但未考虑充电策略。如2.6节所示,此基准方法对Dijkstra进行改进并采用完全充电策略,即每次在充电桩节点充电时都将电量充满,以验证部分充电策略的有效性。
(2) RL & Dueling DQN。与本文相同,此方法结合Dueling DQN算法对Q值进行近似。然而,强化学习中的奖励凭借人为经验进行设置,用此基准方法可验证逆强化学习算法获得的奖励函数的优越性。
(3) RL & DQN。与方法(2)相同,此方法的奖励同样人为给定, 且与方法(2)设置相同的奖励,并通过经典的DQN算法对Q值进行近似,此方法用来验证Dueling DQN算法的有效性。
3.3 评价标准本文从有效性和高效性两方面对模型进行评价。在有效性评估方面,对于电动汽车的出行规划,行驶时间(Tpath)以及充电时间(Tch)两个基本评价指标尤为重要,直接影响电动汽车的出行效率。此外,充电频率(Frqch)高会导致充电服务时间长,因此充电频率也是一个重要的评价指标,本文用路径中包含的充电次数对该指标进行衡量。除上述3个评价指标外,由于用户在行驶过程中希望尽可能避免绕路,因此绕路次数也值得关注,这一指标用loop值衡量。因此本文对于有效性的评价指标包括:行驶时间、充电时间、充电频率、绕路次数。本文用Gap来量化所提出的方法与基准方法之间的差异,前两个指标的Gap表示为
| $ \;\;\;\;\;\;\;\;\;\;\;\operatorname{Gap}\left(T_{\text {path }}\right)=\frac{\operatorname{ExistF}\left(T_{\text {path }}\right)-\operatorname{PropF}\left(T_{\text {path }}\right)}{\operatorname{PropF}\left(T_{\text {path }}\right)} \times \\ 100\%, $ |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\operatorname{Gap}\left(T_{\mathrm{ch}}\right)=\frac{\operatorname{ExistF}\left(T_{\mathrm{ch}}\right)-\operatorname{PropF}\left(T_{\mathrm{ch}}\right)}{\operatorname{PropF}\left(T_{\mathrm{ch}}\right)} \times \\ 100 \%, \end{array} $ |
式中,ExistF表示基准方法的性能,PropF表示本文提出的方法的性能;GapTpath和GapTch分别表示两种方法之间行驶时间以及充电时间的差异。由于后面两个指标中PropF的值可能为0,因而直接用两种方法的差值表示Gap,类似地可表示为
| $ \mathrm{Gap}\left(\mathrm{Frq}_{\mathrm{ch}}\right)=\operatorname{ExistF}\left(\mathrm{Frq}_{\mathrm{ch}}\right)-\operatorname{PropF}\left(\mathrm{Frq}_{\mathrm{ch}}\right) \text {, } $ |
| $ \operatorname{Gap}(\operatorname{loop})=\operatorname{ExistF}(\operatorname{loop})-\operatorname{PropF}(\operatorname{loop}) 。$ |
Gap的值越大,说明本文提出的方法性能相对基准方法越好。
对于高效性的评估,使用运行模型所需的时间作为评价指标在不同的模型之间进行比较。模型运行时间越短,说明模型越高效。
3.4 实验结果选取8对不同方向的起点、终点对测试各个方法的性能,其中Tpath、Tch、Frqch、loop分别表示8条路径的平均行驶时间、平均充电时间、平均充电频率以及平均绕路次数,利用这些指标对模型的有效性进行验证。路网Ⅰ、Ⅱ中4个评估指标下所有模型的结果如表 1所示。
| 路网 Road network |
方法 Methods |
Tpath | Tch | Frqch | loop |
| Ⅰ | Dijkstra & Full charge | 773.921 | 235.348 | 1.875 | 0 |
| RL & Dueling DQN | 843.072 | 248.438 | 2.500 | 0.750 | |
| RL & DQN | 858.768 | 259.819 | 2.750 | 1.125 | |
| Proposed method | 778.904 | 212.078 | 1.750 | 0 | |
| Ⅱ | Dijkstra & Full charge | 1 987.090 | 608.630 | 5.750 | 0 |
| RL & Dueling DQN | 2 036.660 | 627.320 | 6.750 | 2.375 | |
| RL & DQN | 2 063.460 | 639.570 | 7.375 | 3.250 | |
| Proposed method | 1 993.900 | 592.360 | 5.375 | 0 | |
| Note: The best results of each evaluation criterion in the test set are shown in bold | |||||
由表 1可知,由于Dijkstra算法一定能得到最短路径且不存在绕路情况,因此Dijkstra &完全充电策略在行驶时间和绕路方面在所有方法中表现最佳,而本文方法在行驶时间方面与Dijkstra算法的差距很小,且同样不存在绕路情况。在充电性能方面,由于Dijkstra &完全充电策略不考虑电量的可用性,相对本文方法表现较差,说明部分充电策略在提高充电效率上具有有效性。此外,Dijkstra算法的充电次数也多于本文方法,说明本文方法在决策时考虑增加路径代价以节约充电代价,从而使得整个旅程的代价(行驶时间与充电时间相加)最小,这一点可以通过将前两个指标相加来证明。Dijkstra &完全充电策略的Tpath+Tch大于本文方法,就整个旅程的代价而言,本文方法优于Dijkstra &完全充电策略。对于RL & Dueling DQN以及RL & DQN两种强化学习方法,其行驶时间以及充电两方面的性能表现均不佳,且部分路径存在绕路情况,原因可能是奖励凭借人为经验设定,在复杂问题中难以考虑全面。此外,使用Dueling DQN的方法表现比使用DQN的方法好,说明Dueling DQN算法的有效性。综上可知,相较于基准方法,结合逆强化学习算法与Dueling DQN的模型,在对电动汽车进行出行规划时,可以得到使整个旅程代价最小的出行方案,证明了本文模型的有效性。
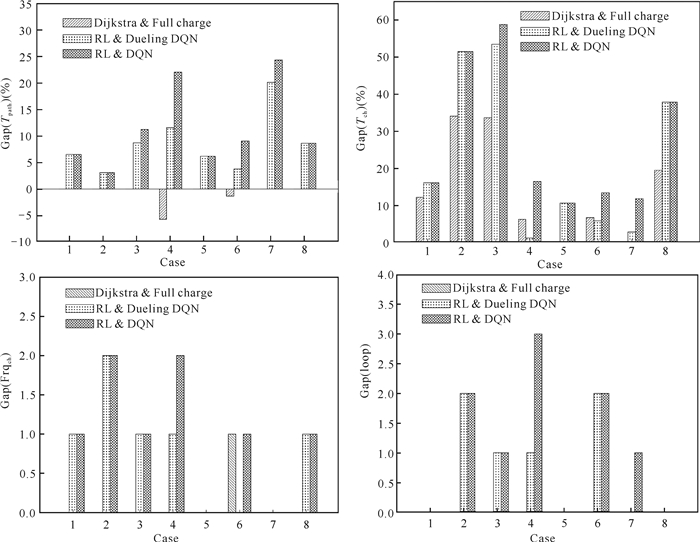
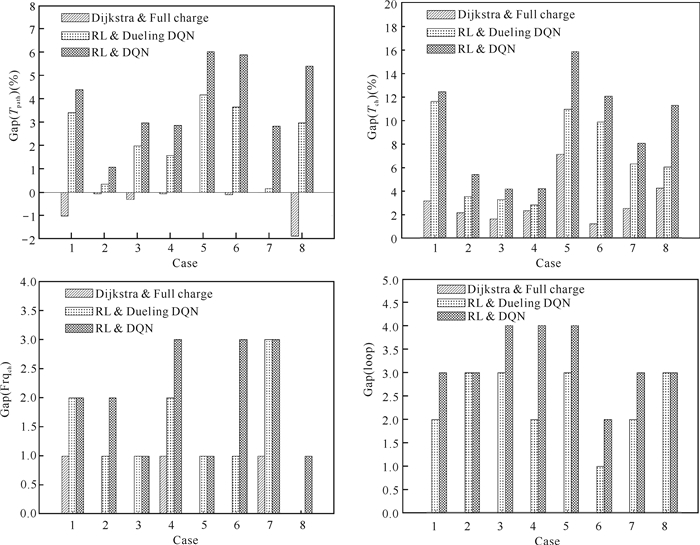
通过Gap详细对比不同方法生成的每条路径,将起点、终点对相同的路径归为一组,路网Ⅰ中的结果对比如图 7所示,路网Ⅱ中的结果对比如图 8所示。本文模型在绝大多数路径中表现最为优秀。
|
| 图 7 路网Ⅰ中不同方法生成的路径结果对比 Fig. 7 Comparison of path results generated by different methods in road network Ⅰ |
|
| 图 8 路网Ⅱ中不同方法生成的路径结果对比 Fig. 8 Comparison of path results generated by different methods in road network Ⅱ |
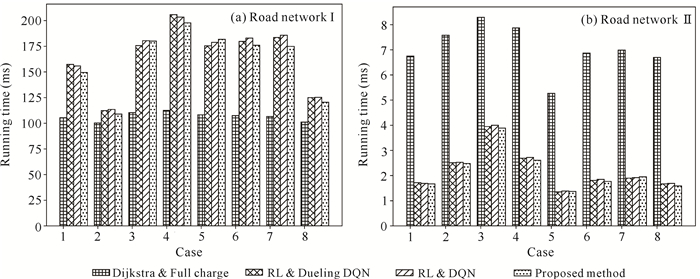
为验证模型的高效性,对路网Ⅰ、Ⅱ模型的运行时间进行对比,如图 9所示。在高效性验证中,Dijkstra算法在较小的路网中运行时间略微短于强化学习以及逆强化学习模型。然而Dijkstra算法的运行时间与路网规模强相关,因此在大型路网中,Dijkstra算法的运行时间远远长于强化学习模型与逆强化学习模型。这也证明了本文模型在大型路网中的高效性。
|
| 图 9 模型运行时间对比 Fig. 9 Comparison of model running time |
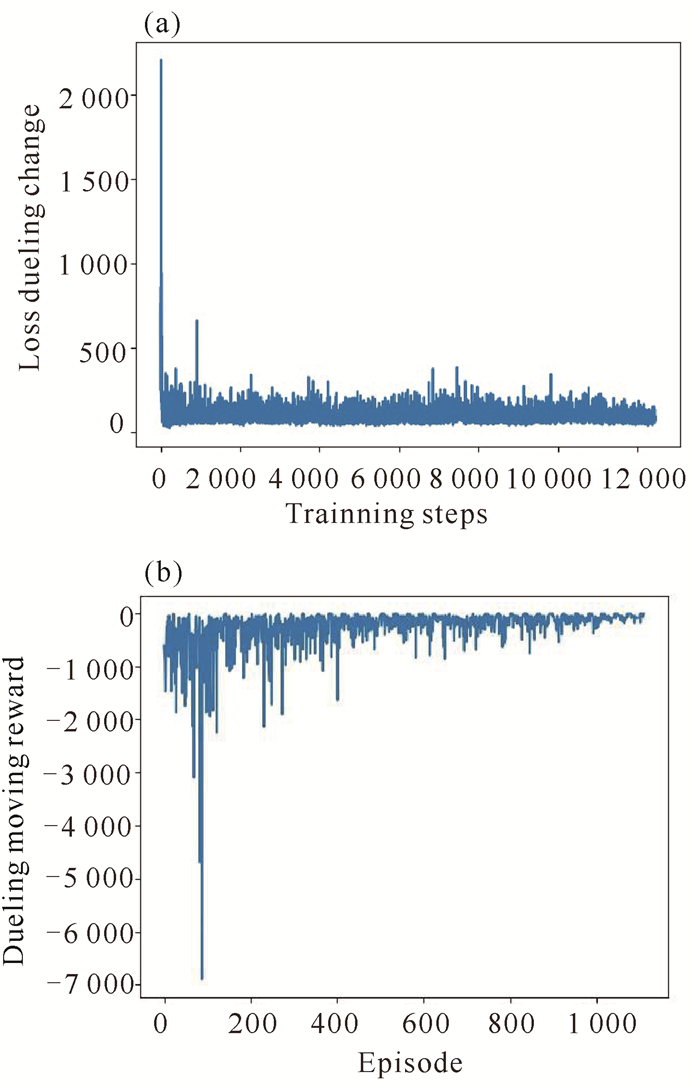
该模型的收敛性如图 10所示,在训练一定轮数后每一轮获得的奖励值趋于稳定且神经网络的参数也逐渐收敛。
|
| 图 10 模型收敛性 Fig. 10 Convergence of model |
此外,训练出来的模型也能较好地直接应用在其他路网上而无需重新训练,而Dijkstra算法不具备此特点。处理不同的路网时,Dijkstra算法需要重新进行数据预处理而不能将原有模型直接应用在新路网中,即不具备迁移性。本文在两个未经训练的新路网中运行模型用以验证迁移性,在路网Ⅲ和路网Ⅳ中随机设置起点、终点对运行模型,观察能否得到可达路径,利用可达路径的比例评估不同模型的迁移性。在两个路网中各模型的可达路径比例如表 2所示,本文模型在两个路网中均表现最佳。
| 路网 Road network |
Model migration (%) | ||
| RL & Dueling DQN | RL & DQN | Proposed method | |
| Ⅲ | 74 | 68 | 86 |
| Ⅳ | 70 | 62 | 80 |
| Note: The best results of each evaluation criterion in the test set are shown in bold | |||
4 结论
本文将考虑充电行为的Dijkstra算法生成的轨迹作为专家示例,使用Dueling DQN算法对Q值近似,提出了一种基于逆强化学习的电动汽车出行规划方法。该方法能够有效引导电动汽车用户选择一条可达目的地,并且行驶时间短、充电时间短、充电频率少的路线行走。通过引入分段充电以及部分充电策略,使研究场景更接近现实情况,从而有效地提高了充电效率;并利用北京市真实路网中的部分路网图对模型进行评估,结果表明,本文提出的方法优于其他基准方法。此外,本文方法具有很好的迁移性,可以有效地应用在其他未经训练的路网中。在后续的研究中,基于现有方法策略以及实验结果,本文模型可引入非线性奖励函数形式,进一步挖掘特征向量之间的联系以得到更适用的奖励函数,从而提升模型的性能。
| [1] |
赵云峰, 杨武双, 李榕杰, 等. 我国纯电动汽车发展趋势分析[J]. 汽车工程师, 2020(7): 14-17. |
| [2] |
孙叶, 刘锴. 里程焦虑对纯电动汽车使用意愿的影响[J]. 武汉理工大学学报(交通科学与工程版), 2017, 41(1): 87-91. DOI:10.3963/j.issn.2095-3844.2017.01.017 |
| [3] |
CUCHY ' M, JAKOB M. Electric vehicle travel planning with lazy evaluation of recharging times[C]//2019 IEEE International Conference on Systems, Man and Cybernetics (SMC). Bari, Italy: IEEE, 2019: 3168-3173.
|
| [4] |
郭戈, 张振琳. 电动车辆路径优化研究与进展[J]. 控制与决策, 2018, 33(10): 1729-1739. |
| [5] |
LU J, CHEN Y N, HAO J K, et al. The time-dependent electric vehicle routing problem: Model and solution[J]. Expert Systems with Applications, 2020, 161: 113593. DOI:10.1016/j.eswa.2020.113593 |
| [6] |
LEBEAU P, DE CAUWER C, VAN MIERLO J, et al. Conventional, hybrid, or electric vehicles: Which technology for an urban distribution centre?[J]. The Scientific World Journal, 2015, 2015: 302867. DOI:10.1155/2015/302867 |
| [7] |
FELIPE Á, ORTUÑO M T, RIGHINI G, et al. A heuristic approach for the green vehicle routing problem with multiple technologies and partial recharges[J]. Transportation Research Part E: Logistics and Transportation Review, 2014, 71: 111-128. DOI:10.1016/j.tre.2014.09.003 |
| [8] |
CANDRA A, BUDIMAN M A, HARTANTO K. Dijkstra's and A-Star in finding the shortest path: A Tutorial[C]//2020 International Conference on Data Science, Artificial Intelligence, and Business Analytics (DATABIA). Medan, Indonesia: IEEE, 2020: 28-32.
|
| [9] |
KOBAYASHI Y, KIYAMA N, AOSHIMA H, et al. A route search method for electric vehicles in consideration of range and locations of charging stations[C]//2011 IEEE Intelligent Vehicles Symposium (Ⅳ). Baden-Baden, Germany: IEEE, 2011: 920-925.
|
| [10] |
WANG Y, JIANG J M, MU T T. Context-aware and energy-driven route optimization for fully electric vehicles via crowdsourcing[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(3): 1331-1345. DOI:10.1109/TITS.2013.2261064 |
| [11] |
YANG C, TANG J R, SHEN Q. Impact of electric vehicle battery parameters on the large-scale electric vehicle charging loads in power distribution network[C]//2020 16th International Conference on Control, Automation, Robotics and Vision (ICARCV). Shenzhen, China: IEEE, 2020: 56-60.
|
| [12] |
KESKIN M, AKHAVAN-TABATABAEI R, ÇATAY B. Electric vehicle routing problem with time windows and stochastic waiting times at recharging stations[C]//2019 Winter Simulation Conference (WSC). National Harbor, MD, USA: IEEE, 2019: 1649-1659.
|
| [13] |
HANAWAL M K, LIU H, ZHU H H, et al. Learning policies for Markov decision processes from data[J]. IEEE Transactions on Automatic Control, 2019, 64(6): 2298-2309. DOI:10.1109/TAC.2018.2866455 |
| [14] |
HE M X, LU D J, TIAN J, et al. Collaborative rein- forcement learning based route planning for cloud content delivery networks[J]. IEEE Access, 2021, 9: 30868-30880. DOI:10.1109/ACCESS.2021.3060440 |
| [15] |
CHREN W A. One-hot residue coding for high-speed non-uniform pseudo-random test pattern generation[C]//Proceedings of ISCAS'95-International Symposium on Circuits and Systems. Seattle, WA, USA: IEEE, 1995, 1: 401-404.
|
| [16] |
ABBEEL P, NG A Y. Apprenticeship learning via inverse reinforcement learning[C]//Proceedings of the 21st International Conference on Machine Learning. Banff, Canada: ACM, 2004.
|
| [17] |
QIU H M, LIU F. A state representation dueling network for deep reinforcement learning[C]//2020 IEEE 32nd International Conference on Tools with Artificial Intelligence (ICTAI). Baltimore, MD, USA: IEEE, 2020: 669-674.
|
| [18] |
WINARNO E, HADIKURNIAWATI W, ROSSO R N. Location based service for presence system using haversine method[C]//2017 International Conference on Innovative and Creative Information Technology (ICITech). Salatiga, Indonesia: IEEE, 2017: 1-4. DOI: 10.1109/INNOCIT.2017.8319153.
|
| [19] |
ABOUSLEIMAN R, RAWASHDEH O. A Bellman- Ford approach to energy efficient routing of electric vehicles[C]//2015 IEEE Transportation Electrification Conference and Expo (ITEC). Dearborn, MI, USA: IEEE, 2015: 1-4.
|
| [20] |
YI L M. Lane change of vehicles based on DQN[C]//2020 5th International Conference on Information Science, Computer Technology and Transportation (ISCTT). Shenyang, China: IEEE, 2020: 593-597.
|
| [21] |
SHARMA J, ANDERSEN P A, GRANMO O C, et al. Deep Q-learning with Q-matrix transfer learning for novel fire evacuation environment[J]. IEEE Transactions on Systems, Man and Cybernetics: Systems, 2021, 51(12): 7363-7381. |
| [22] |
SONG S N, FANG Z Y, ZHANG Z Y, et al. Semi-online computational offloading by Dueling Deep-Q network for user behavior prediction[J]. IEEE Access, 2020, 8: 118192-118204. DOI:10.1109/ACCESS.2020.3004861 |
| [23] |
FAN D K, SHI P. Improvement of Dijkstra's algorithm and its application in route planning[C]//2010 Seventh International Conference on Fuzzy Systems and Knowledge Discovery. Yantai, China: IEEE, 2010, 4: 1901-1904.
|
| [24] |
KESSWANI N. Performance evaluation of shortest path routing algorithms in real road networks[C]//Proceedings of the International Conference on Data Engineering and Communication Technology. Singapore: Springer, 2017: 77-83.
|
| [25] |
DESAULNIERS G, ERRICO F, IRNICH S, et al. Exact algorithms for electric vehicle-routing problems with time windows[J]. Operations Research, 2016, 64(6): 1388-1405. DOI:10.1287/opre.2016.1535 |



