2. 湖北工业大学理学院, 湖北武汉 430068
2. School of Science, Hubei University of Technology, Wuhan, Hubei, 430068, China
近年来,随着我国工业化进程不断加快,经济迅猛发展,人口不断增长,空气污染问题已经引起全社会的关注[1]。建立空气质量预测模型对城市环境治理工作有着重要作用,不仅有助于减轻大气污染对人体的伤害,还能为环保部门准确预测空气质量提供科学的方法[2]。
空气质量指数(Air Quality Index,AQI)的传统预测方法有时间序列模型、数理统计模型、线性回归模型、灰色预测方法等[3, 4]。天气、大气污染物等因素对空气质量具有较大影响,导致空气质量具有明显的非线性、不确定性等特征。因此,传统的预测方法很难得到精确的预测结果[5]。由于神经网络具有较强的非线性拟合能力,可以较好地完成对AQI的预测。王国胜等[6]采用BP神经网络模型对AQI进行预测,结果相较于传统统计方法,虽然得到了更高的预测精度,但是单一BP神经网络收敛速度慢且易陷入局部最优解。为了进一步提高预测精度,有学者利用智能优化算法对其进行优化,如张旭等[7]利用粒子群算法(Particle Swarm Optimization,PSO)优化BP神经网络,提升了模型的泛化能力,在空气质量指数预测中取得较好效果。杨云等[8]利用遗传算法(Genetic Algorithm,GA)对BP神经网络进行改进,建立空气质量指数预测模型,提升了BP神经网络的性能,预测结果有更高的精度。综上所述,传统的单一BP神经网络模型的AQI预测效果较差,尽管有些学者利用传统优化算法优化模型,在一定程度上解决了预测精度的问题,但在算法迭代后期仍存在易陷入局部最优、收敛速度慢的缺点。
为解决上述问题,本研究利用改进麻雀搜索算法(Improved Sparrow Search Algorithm,ISSA),对BP神经网络进行训练,以期得到预测精度高、全局搜索能力强的ISSA-BP模型。该模型的主要思路是利用麻雀搜索算法(Sparrow Search Algorithm,SSA)相较于传统优化算法具有收敛速度快、寻优精度高的优点[9],对BP神经网络的权值及阈值进行优化,同时考虑到SSA在迭代后期,存在种群多样性减少、收敛速度慢以及全局搜索能力弱的缺陷[10],通过引入立方映射提高初始解的质量,增加初始化麻雀种群的多样性,从而提升算法的收敛能力,同时结合优化策略增强算法的全局搜索能力。使用ISSA-BP模型对杭州市空气质量指数值进行预测,检验该模型的实际应用效果。
1 麻雀搜索算法(SSA)麻雀搜索算法是模拟麻雀搜索食物过程的一种新型智能算法[11],通过比较适应度值,不断更新种群中麻雀个体的位置。
在SSA中,发现者搜索范围广,负责引导种群搜索和觅食,发现者的位置更新公式如下:
| $ X_{i, d}^{t+1}=\left\{\begin{array}{l} X_{i, d}^t \exp \left(\frac{-i}{\alpha t_{\max }}\right), R<S T, \\ X_{i, d}^t+Q L, R \geqslant S T \end{array}, \right. $ | (1) |
式(1)中,d表示搜索空间维度,t表示当前的迭代次数,tmax表示最大迭代次数,α是(0, 1]间的均匀随机数。Xi, dt表示第t次迭代下,第i只麻雀处于d维的位置。R为预警值,取值范围为[0, 1]。ST为警戒值,取值范围为[0.5, 1]。Q为服从标准正态分布的随机数。L为一个单行d维的全1矩阵。
跟随者会跟随发现者进行觅食以获得更好的适应度,其位置更新公式如下:
| $ X_{i, d}^{t+1}=\left\{\begin{array}{l} Q \exp \left(\frac{X_{\text {worst }}^t-X_i^t}{i^2}\right), i>\frac{n}{2} \\ X_p^{t+1}+\left|X_{i, d}^t-X_p^{t+1}\right| A^{+} L, \text { 其他 } \end{array}, \right. $ | (2) |
式(2)中,Xpt+1为第t+1次迭代发现者最优位置,Xworstt为第t次迭代全局最差位置。A为一个单行d维的矩阵,其中每个元素随机赋值为1或-1,且A+=AT(AAT)-1,n为麻雀总数。
在麻雀觅食的同时会在种群中随机选取一定比例的个体作为警戒者进行侦查预警,其位置更新公式如下:
| $ X_{i, d}^{t+1}=\left\{\begin{array}{l} X_{\text {best }}^t+\beta\left|X_{i, d}^t-X_{\text {best }}^t\right|, f_{\mathrm{i}}>f_{\mathrm{g}} \\ X_{i, d}^t+K\left(\frac{\left|X_{i, d}^t-X_{\text {worst }}^t\right|}{\left(f_{\mathrm{i}}-f_{\mathrm{w}}\right)+\xi}\right), f_{\mathrm{i}}=f_{\mathrm{g}}, \end{array}\right. $ | (3) |
式(3)中,Xbestt为第t次迭代全局最优位置,β为步长控制参数,K为[-1, 1]的随机数。ξ是一个极小常数,用以避免当fi=fw时,分母为0的情况。fi、fg、fw分别表示当前、最佳和最差适应度。
2 改进的麻雀搜索算法(ISSA) 2.1 立方映射初始化种群麻雀搜索算法对种群进行初始化时,采用的是随机生成的方式,这种方式会使得麻雀种群分布不均匀,影响后期的迭代寻优。为提高算法全局搜索能力,避免迭代后期种群多样性降低,同时考虑到混沌映射具有随机性、遍历性和规律性等特点[12, 13],利用混沌序列对种群进行初始化。汤安迪等[14]证明了立方映射的均匀性及遍历性优于经典的Logistic映射,故本研究采用立方映射完成种群的初始化。立方映射公式如下:
| $ y(n+1)=4 y(n)^3-3 y(n), $ | (4) |
式(4)中,n为映射次数,y(n)∈(-1, 0)∪(0, 1),y(n)为第n次映射值。
为防止通过立方映射产生的值超过BP神经网络的权值及阈值优化范围,利用式(5)将映射值调整到统一区间:
| $ X_i=X_{l b}+0.5\left(X_{l b}-X_{u b}\right)\left(y_i+1\right) $ | (5) |
式(5)中,Xlb、Xub分别为麻雀种群中个体所处维度的上、下边界;Xi为麻雀个体实际位置值。
立方映射初始化麻雀种群的步骤如下:
步骤1 设置种群规模N、维数d、初始值y0。
步骤2 根据式(4)进行迭代计算,产生序列y,序列y中每个d维向量作为一个麻雀个体。
步骤3 根据式(5)对越界值进行处理,使得每个d维向量的值变化区间是[-1, 1]。
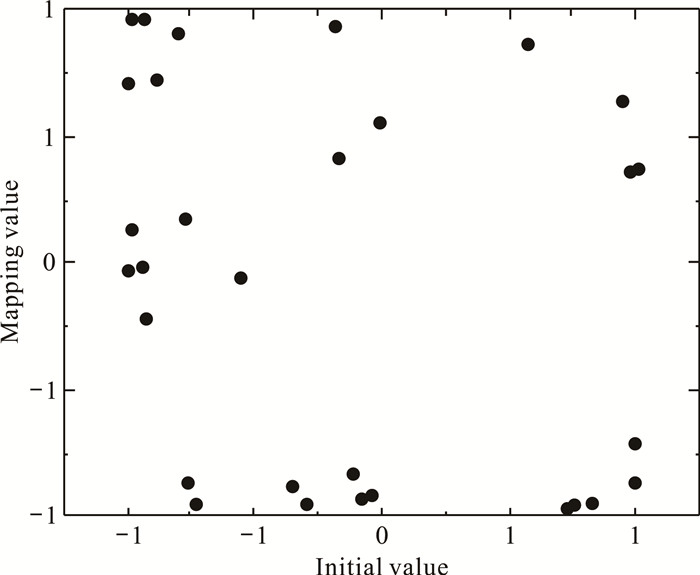
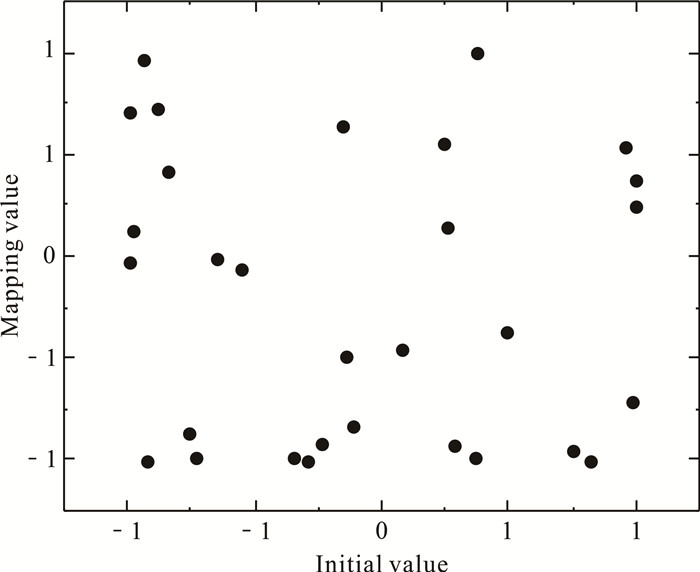
假设种群规模为30,在二维搜索空间中产生的初始化种群分布如图 1和图 2所示,从图中可以看出,相比随机初始化的种群序列,通过立方映射产生的初始种群分布更加均匀,遍历性更好。
|
| 图 1 随机初始化种群 Fig. 1 Random initialization population |
|
| 图 2 立方映射初始化种群 Fig. 2 Cube mapping initialization population |
2.2 蝴蝶优化策略
蝴蝶优化算法(Butterfly Optimization Algorithm,BOA)是受到蝴蝶觅食和求偶过程所启发的群智能算法[15]。在迭代时,蝴蝶将朝着气味最浓的方向移动,该阶段被称为全局搜索阶段。其位置更新方式如下:
| $ X_i^{t+1}=X_i^t+\left(r^2 X_{\text {gbest }}-X_i^t\right) f_i, $ | (6) |
式(6)中,Xit是第t次迭代过程中第i只蝴蝶的位置,Xgbest是当前全局最优位置,fi表示第i只蝴蝶发出的气味,其取值大小取决于适应度的大小,r为0-1的随机数。
由式(1)可知,当R<ST时,虽然随着迭代次数的增大,取值分布变得较为均匀,在一定程度上提高了其收敛速度,但是发现者的每一维都在变小并逐渐收敛于0,因此其搜索能力在逐渐降低,这会导致算法在迭代后期易陷入局部极值的情况。故本研究利用BOA的全局搜索阶段位置更新策略改进式(1),改进后的公式如下:
| $ X_{i, d}^{t+1}=\left\{\begin{array}{l} X_{i, d}^t+\left(r^2 X_{\text {best }}^t-X_{i, d}^t\right) f_i, R<S T \\ X_{i, d}^t+Q L, R \geqslant S T \end{array}\right. \text { 。} $ | (7) |
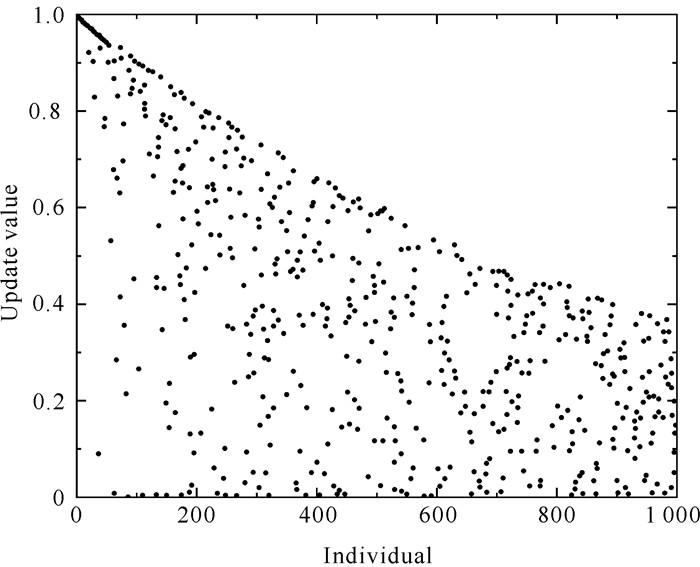
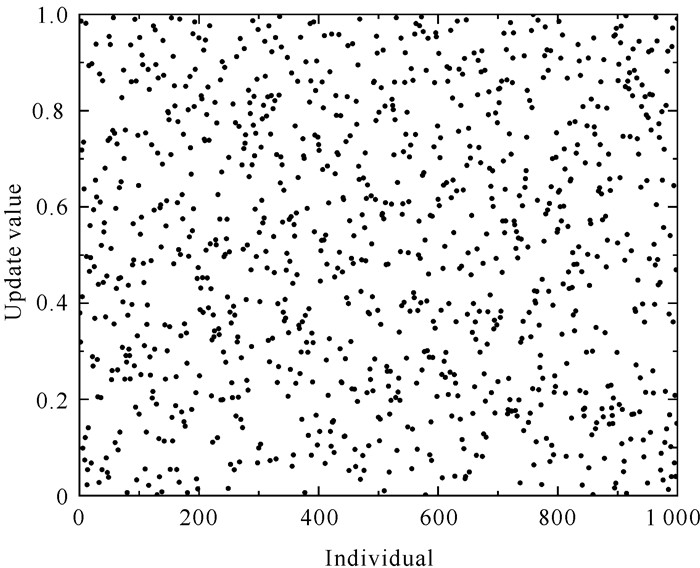
对改进前后的公式分别进行迭代,得到麻雀种群中个体的分布如图 3和图 4所示。从图中可以看出,改进后的策略在迭代后期保证了麻雀种群个体分布的多样性,在提高收敛速度的同时,在一定程度上扩大了搜索空间,提升了算法的全局寻优能力。
|
| 图 3 改进前发现者搜索策略 Fig. 3 Discoverer search strategy before improvement |
|
| 图 4 改进后发现者搜索策略 Fig. 4 Discoverer search strategy after improvement |
2.3 正余弦搜索策略
根据式(2)可知,跟随者在向发现者最优位置靠近时,会导致种群个体短时间聚集,虽然提高了算法的收敛速度,但是易出现算法陷入局部最优。正余弦函数不仅易于实现,而且有着良好的收敛性。利用其振荡特性进行寻优可以降低算法易陷入局部最优解的风险。改进后跟随者的位置更新公式如下:
| $ \begin{array}{l} \;\;\;\;\;\;X_{i, d}^{t + 1} = \\ \left\{ {\begin{array}{*{20}{l}} {X_{i, d}^t + {S_1} \cdot \sin \left( {{S_2}} \right) \cdot \left| {{S_3} \cdot X_{{\rm{best }}}^t - X_{i, d}^t} \right|, {S_4} < 0.5}\\ {X_{i, d}^t + {S_1} \cdot \cos \left( {{S_2}} \right) \cdot \left| {{S_3} \cdot X_{{\rm{best }}}^t - X_{i, d}^t} \right|, {S_4} \ge 0.5} \end{array}, } \right. \end{array} $ | (8) |
| $ S_1=a\left(1-\frac{t}{t_{\max }}\right), $ | (9) |
式(8)(9)中:a为大于1的常数,本研究中的a取2;S1、S2、S3、S4均为服从均匀分布的随机数;S2∈(0, 2π)、S3∈(0, 2)、S4∈(0, 1);tmax为最大迭代次数。
2.4 高斯扰动策略高斯分布在局部空间搜索性能好,对全局最优个体使用高斯扰动有利于算法跳出局部极值点,同时也增强了算法全局搜索性能。使用高斯扰动策略生成新个体的公式如下:
| $ X_{\mathrm{Gbest}}^t=X_{\text {best }}^t\left(1+\operatorname{Gaussian}\left(u, \sigma^2\right)\right), $ | (10) |
式(10)中,Xbestt为当前全局最优位置,XGbestt为高斯变异后得到的个体位置。u和σ2为高斯分布的均值和方差,本研究中的u取0,σ2取1。
2.5 算法性能测试 2.5.1 算法初始化参数设置为了验证ISSA的寻优效果与稳定性,本研究选取遗传算法(Genetic Algorithm,GA)[16]、粒子群算法(Particle Swarm Optimization, PSO)[17]、SSA以及ISSA进行寻优结果的对比,同时为了保持所有初始种群分布的均匀性与多样性,随机产生的每维取值范围均是[-1, 1]的30维向量y0,作为种群的第一个个体,后续种群个体利用上述立方映射公式进行种群初始化。设置种群中的边界范围为[-3, 3],通过上述立方映射的边界值处理公式将种群中所有个体的取值范围统一为[-1, 1],其中所有算法的种群数量设置为30,最大迭代次数为1 000。
2.5.2 测试函数选取为了进一步验证ISSA的寻优性能,采用8个具有不同特征的基准测试函数进行测试。其中,F1-F5是单峰函数,F6-F8是多峰函数,测试函数维度为30,寻优的最优值为0,8个基准测试函数及其具体信息如表 1所示。
| 函数名称 Function name |
测试函数 Test function |
维度 Dimension |
搜索范围 Search scope |
最优值 Optimal value |
| Sphere | 30 | [-100, 100] | 0 | |
| Schwefel 1.2 | 30 | [-100, 100] | 0 | |
| Schwefel 2.22 | 30 | [-10, 10] | 0 | |
| Rosenbrock | 30 | [-30, 30] | 0 | |
| Step | 30 | [-100, 100] | 0 | |
| Griewank | 30 | [-600, 600] | 0 | |
| Rastrigin | 30 | [-5.12, 5.12] | 0 | |
| Ackley | 30 | [-32, 32] | 0 |
2.5.3 算法寻优能力分析
为了去除偶然性带来的误差,分别利用上述4种算法对8个测试函数进行30次独立试验,以0.01为取值间隔,通过参数值在对应取值范围内的不断遍历,选取30次最优值的平均值作为算法的寻优结果,选取历史最优值对应的算法参数值作为算法参数的最佳取值。算法的最佳参数值及测试函数的寻优结果分别如表 2和表 3所示。
| 算法 Algorithm |
参数 Parameter |
取值范围 Value range |
最佳取值 Optimal value |
| GA | Crossover probability Pc | [0, 1] | 0.8 |
| Mutation probability Pm | [0, 1] | 0.2 | |
| PSO | Individual acceleration constant C1 | [0, 4] | 2.0 |
| Social acceleration constant C2 | [0, 4] | 2.0 | |
| Inertia weight w | [0, 1] | 0.9 | |
| SSA | Warning value ST | [0.5, 1] | 0.8 |
| Alarm value R | [0, 1] | 0.2 | |
| Proportion of vigilantes SD | [0, 1] | 0.2 | |
| ISSA | Warning value ST | [0.5, 1] | 0.8 |
| Alarm value R | [0, 1] | 0.2 | |
| Proportion of vigilantes SD | [0, 1] | 0.2 |
| 函数Function | 算法Algorithm | 最优值Optimal value | 平均值Average value | 标准差Standard deviation | 函数Function | 算法Algorithm | 最优值Optimal value | 平均值Average value | 标准差Standard deviation | |
| F1 | GA | 2.11 | 4.43 | 1.98 | F5 | GA | 18.89 | 70.35 | 45.69 | |
| PSO | 0.55 | 0.75 | 0.71 | PSO | 0.87 | 1.15 | 0.24 | |||
| SSA | 6.5e-178 | 1.2e-91 | 1.74e-91 | SSA | 1.7e-09 | 9.9e-06 | 1.6e-05 | |||
| ISSA | 1.3e-200 | 4.9e-112 | 1.1e-111 | ISSA | 5.0e-10 | 5.4e-06 | 6.1e-06 | |||
| F2 | GA | 184.08 | 228.28 | 228.28 | F6 | GA | 58.9 | 66.8 | 7.63 | |
| PSO | 11.24 | 14.31 | 14.31 | PSO | 154 | 198 | 29.9 | |||
| SSA | 2.4e-95 | 3.1e-51 | 3.5e-51 | SSA | 0 | 0 | 0 | |||
| ISSA | 9.4e-179 | 9.2e-61 | 2.1e-60 | ISSA | 0 | 0 | 0 | |||
| F3 | GA | 4.19 | 5.98 | 1.97 | F7 | GA | 0.02 | 0.02 | 0.007 | |
| PSO | 160.05 | 321.10 | 321.10 | PSO | 0.04 | 0.06 | 0.01 | |||
| SSA | 3.2e-18 | 1.1e-15 | 2.4e-15 | SSA | 0 | 0 | 0 | |||
| ISSA | 5.3e-23 | 4.8e-17 | 1.1e-18 | ISSA | 0 | 0 | 0 | |||
| F4 | GA | 3 392.3 | 6 516.9 | 2 806.5 | F8 | GA | 0.01 | 0.02 | 0.009 | |
| PSO | 172.16 | 387.35 | 316.58 | PSO | 0.02 | 0.5 | 0.714 | |||
| SSA | 1.4e-09 | 0.000 9 | 0.001 9 | SSA | 8.9e-16 | 1.6e-15 | 1.6e-15 | |||
| ISSA | 1.8e-14 | 0.000 2 | 0.000 4 | ISSA | 8.9e-16 | 8.9e-16 | 0 |
由表 3可知,ISSA对于单峰函数F1-F3的优化效果非常明显,其寻优的指标值远超其他算法,而对于单峰测试函数F4-F5,虽然ISSA的改进效果略优于SSA,但其改进效果要明显优于GA与PSO,对于多峰函数F8,ISSA的寻优效果与SSA差别不大,但寻优效果优于GA与PSO十几个数量级。不论是单峰函数还是多峰函数,ISSA在多次寻优的过程中, 平均值和标准差均比其他算法更小, 表明ISSA拥有更好的全局搜索能力。
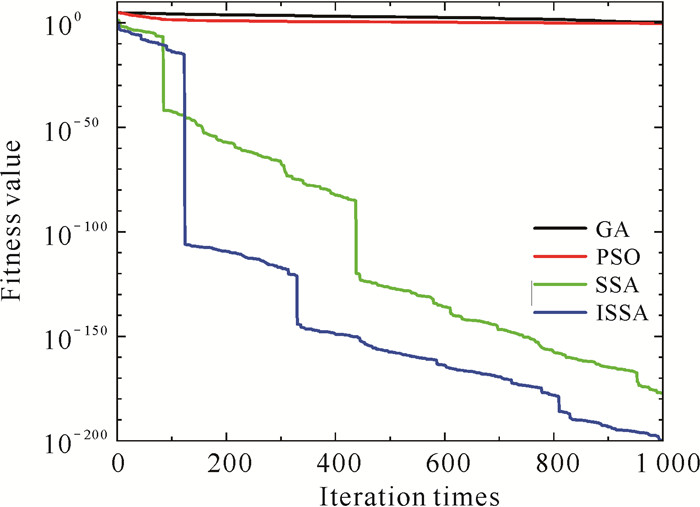
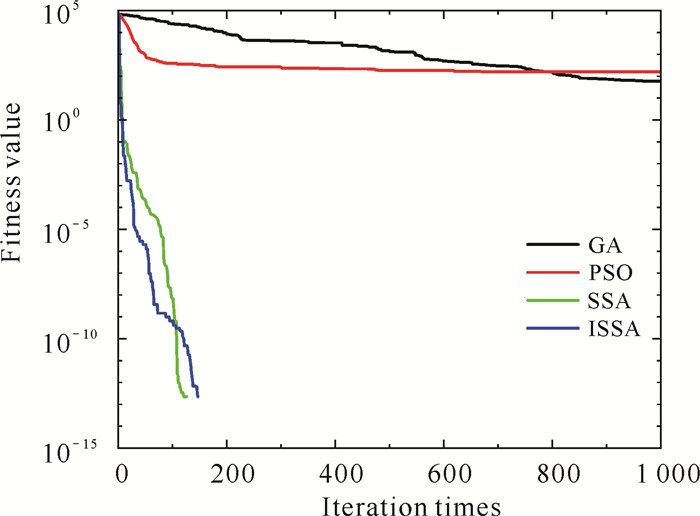
2.5.4 算法收敛能力分析通过绘制基准测试函数迭代进化曲线, 可进一步对比分析各个算法的收敛能力,从而更加精准地评判其预测性能,图 5-12为所有算法迭代1 000次后的进化曲线图。
|
| 图 5 F1进化曲线 Fig. 5 F1 evolution curve |
|
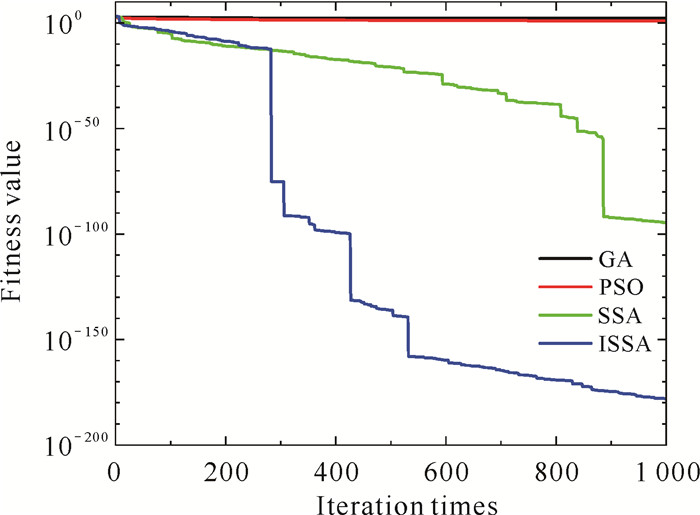
| 图 6 F2进化曲线 Fig. 6 F2 evolution curve |
|
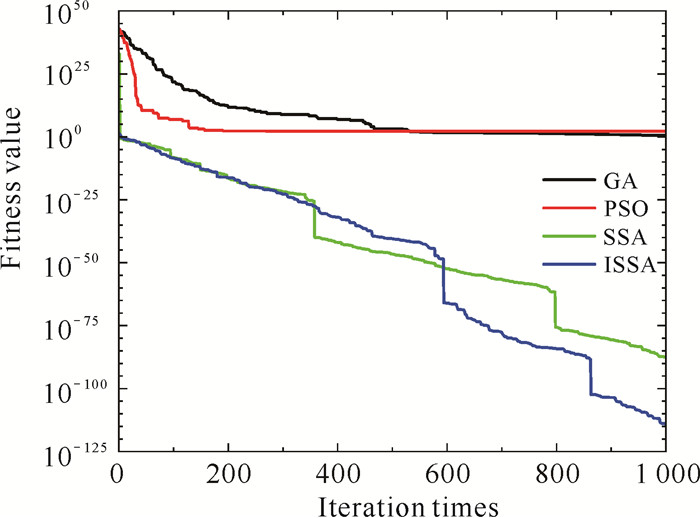
| 图 7 F3进化曲线 Fig. 7 F3 evolution curve |

|
| 图 8 F4进化曲线 Fig. 8 F4 evolution curve |
|
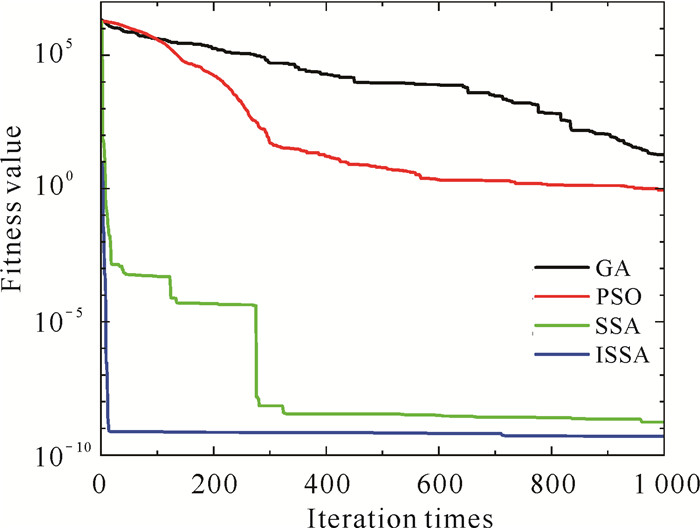
| 图 9 F5进化曲线 Fig. 9 F5evolution curve |
|
| 图 10 F6进化曲线 Fig. 10 F6evolution curve |
|
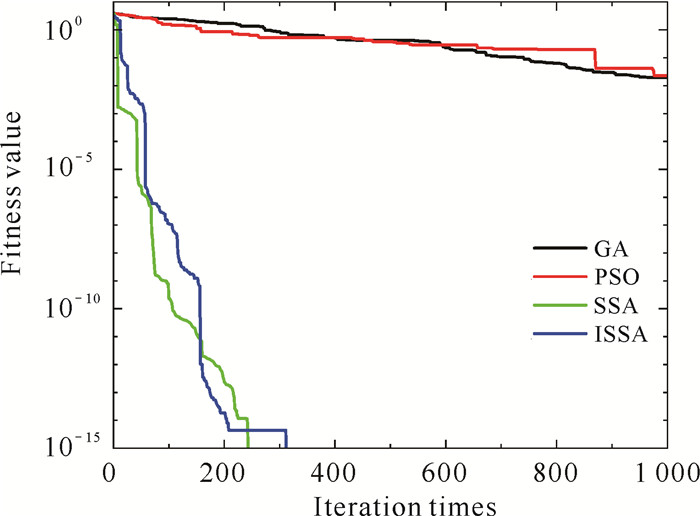
| 图 11 F7进化曲线 Fig. 11 F7evolution curve |
|
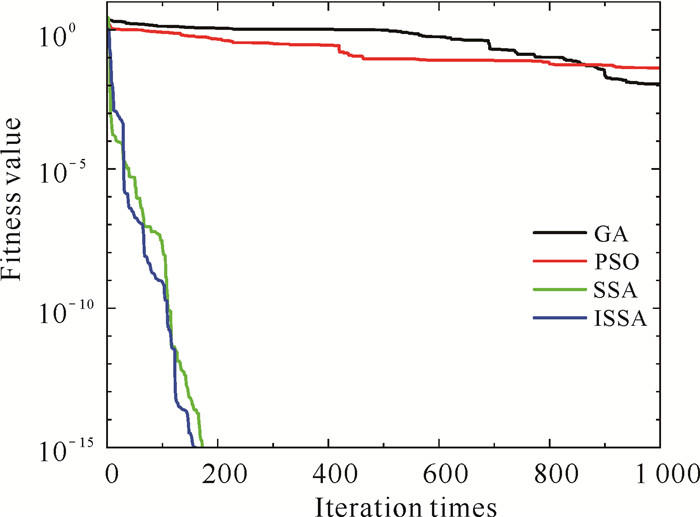
| 图 12 F8进化曲线 Fig. 12 F8 evolution curve |
由图 5-12可知,相比于其他几种算法,一方面,ISSA迭代更少次数进入相同精度, 表明了引入的立方映射提高了初始解的质量,使得种群分布更加均匀;另一方面,当算法的寻优值存在不同程度的停滞时,ISSA的寻优值呈现出波动下降,表明优化策略对算法的改进使得算法有能力跳出局部极值,在全局空间内搜索最优解。以上改进均有效提高了ISSA的收敛速度,使得ISSA相较于其他的算法拥有更强的收敛能力。
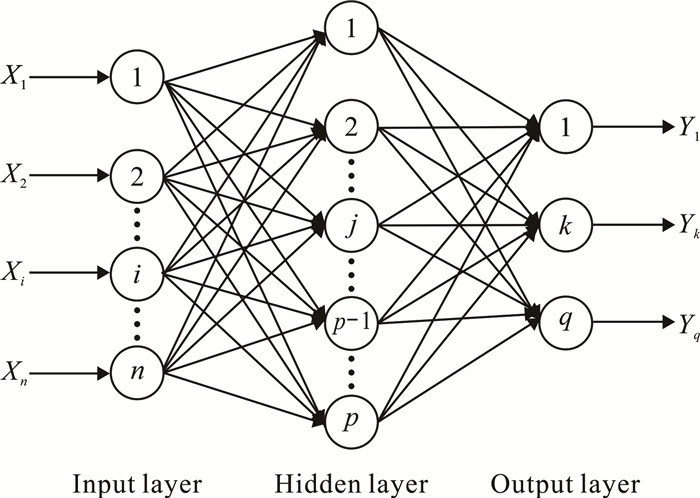
3 ISSA-BP模型 3.1 BP神经网络原理BP神经网络是一种采用误差反向传播算法进行学习的多层前馈网络[18, 19],其结构包括输入层、隐含层、输出层。BP神经网络的拓扑结构如图 13所示。
|
| 图 13 BP神经网络拓扑结构 Fig. 13 BP neural network topological structure |
3.2 ISSA-BP模型原理
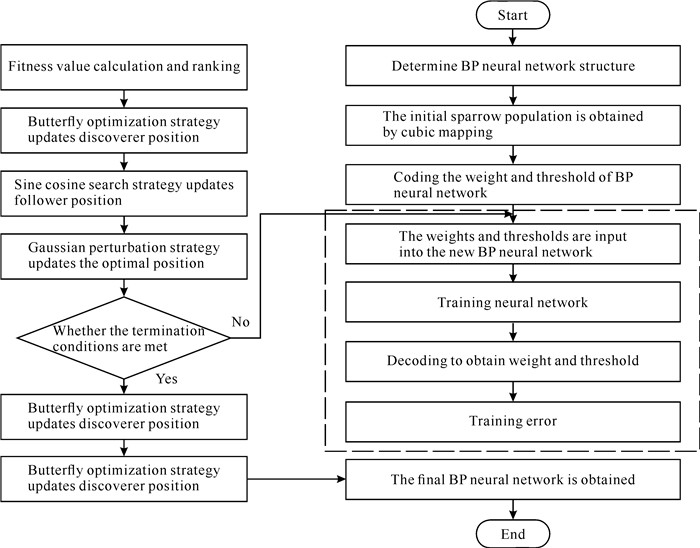
ISSA-BP模型的主要思想是利用改进后的麻雀搜索算法取代梯度下降法在全局范围内对BP神经网络中的权值和阈值进行大范围搜索,通过适应度值的更新不断调整训练误差。本模型将测试集中的均方误差作为适应度函数值。迭代完成后通过解码形成最优权值及阈值,同时结合改进后算法收敛速度快、泛化能力强的特点对BP神经网络进行训练,最后得到预测性能更好的神经网络模型。ISSA-BP模型的流程图如图 14所示。
|
| 图 14 ISSA-BP模型流程图 Fig. 14 Flow chart of ISSA-BP model |
4 基于ISSA-BP模型的AQI预测 4.1 数据采集与预处理
本研究数据是从中华人民共和国生态环境部网站(https://www.mee.gov.cn)实时监测的杭州市空气质量数据中获取的,采样时间为2020年9月1日至2022年1月13日,共计500组样本数据。训练集为随机选取的450组数据,测试集为剩余的50组数据。将PM2.5、PM10、SO2、CO、NO2、O3纳入预测体系中,作为输入变量对AQI进行预测。
由于数据的单位或数量级的不同,可能导致收敛速度变慢、训练时间变长等问题。因此,要对样本数据进行归一化处理,归一化公式如下:
| $ X_k^{\prime}=\frac{X_k-X_{\min }}{X_{\max }-X_{\min }}, $ | (11) |
式(11)中,Xmin为训练集中最小值,Xmax为训练集中最大值,Xk为训练集中任一数值,Xk′为归一化之后的数值。
4.2 BP神经网络结构BP神经网络结构的确定是数据输入以及网络训练的关键,BP神经网络结构包括输入层、输出层以及隐含层3个部分。其中,输入层为6个节点,输出层为1个节点,隐含层节点数是决定BP神经网络预测精度的重要因素[20],神经网络中确定隐含层的神经元数量通常使用经验公式(12)进行计算。
| $ q=\sqrt{m+n}+a, $ | (12) |
式(12)中,q为隐含层的节点个数,m为输入层的节点个数,n为输出层的节点个数,a的取值为1-10的常数。
通过不断改变隐含层神经元数目,并代入神经网络训练,得到的均方误差见表 4。由表 4可知,当隐含层节点数为9时,均方误差最小,因此,本研究选择的隐含层节点数为9。由此可得训练的网络结构为6-9-1。
| 节点数 Number of nodes |
均方误差 Mean square error |
节点数 Number of nodes |
均方误差 Mean square error |
|
| 3 | 0.025 4 | 8 | 0.001 3 | |
| 4 | 0.003 4 | 9 | 0.000 6 | |
| 5 | 0.000 8 | 10 | 0.001 2 | |
| 6 | 0.001 5 | 11 | 0.001 1 | |
| 7 | 0.000 7 | 12 | 0.001 7 |
4.3 仿真实验及结果分析
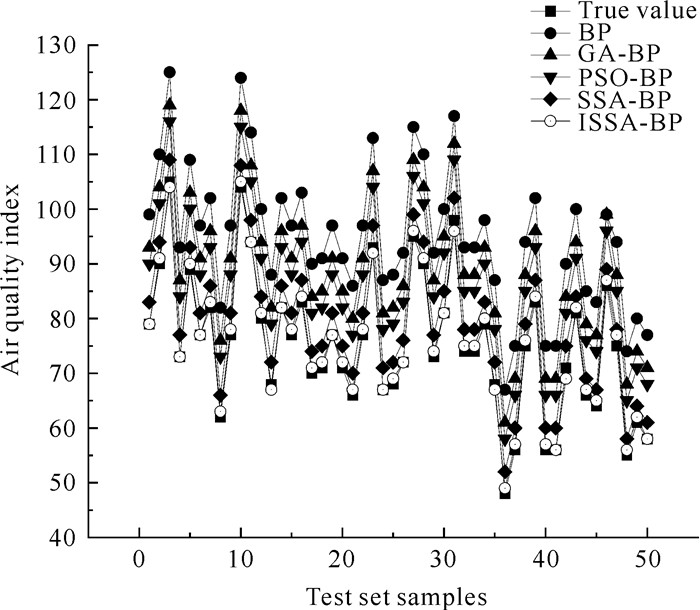
为检验ISSA-BP模型的性能,分别用BP神经网络、遗传算法优化的BP神经网络(GA-BP)、粒子群算法优化的BP神经网络(PSO-BP)、麻雀搜索算法优化的BP神经网络(SSA-BP)作为对照模型进行仿真实验。本研究利用MATLAB进行预测仿真,5种模型的仿真预测结果如图 15所示。
|
| 图 15 模型仿真预测结果 Fig. 15 Model simulation and prediction results |
由仿真结果可知,ISSA-BP模型的预测曲线的拟合程度高于其他4种模型,预测值更加接近真实值,因此,ISSA-BP模型对AQI的预测更加精准。为了对所建立的空气预测模型的性能进行全面而系统的分析,本研究选取均方根误差(Root Mean Square Error, RMSE)、平均绝对误差(Mean Absolute Error, MAE)、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、拟合优度(R2)作为模型优越性的衡量指标。计算公式如下:
| $ \mathrm{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)^2}, $ | (13) |
| $ \mathrm{MAE}=\frac{1}{n} \sum\limits_{i=1}^n\left|\hat{y}_i-y_i\right|, $ | (14) |
| $ \operatorname{MAPE}=\frac{1}{n} \sum\limits_{i=1}^n\left|\frac{\hat{y}_i-y_i}{y_i}\right|, $ | (15) |
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^n {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{y_i} - \bar y} \right)}^2}} }} $ | (16) |
式(13)-(16)中,
利用训练好的模型测试AQI,得到5种预测模型性能的评价结果如表 5所示。由表 5可知,经过相关算法优化后的组合模型的预测效果明显优于单一的BP神经网络模型。其中,在组合模型中,ISSA-BP模型的RMSE、MAE、MAPE数值最小。相比于BP、GA-BP、PSO-BP、SSA-BP模型,ISSA-BP模型的RMSE分别降低了70.8%、50.2%、45.2%、34.6%,MAE分别降低了74.6%、57.9%、54.2%、43.3%,MAPE分别降低了68.2%、53.1%、49.1%、25.2%。决定系数R2为0.99,最接近1,拟合程度最优。因此,本研究提出的ISSA-BP模型的预测精度最好,预测误差最小,能够有效地应用于空气质量指数的预测中。
| 模型 Model |
均方根误差 (RMSE) |
均值绝对误差 (MAE) |
平均绝对百分比误差 (MAPE) |
拟合优度 (R2) |
| BP | 4.15 | 3.66 | 3.55 | 0.89 |
| GA-BP | 2.43 | 2.21 | 2.41 | 0.93 |
| PSO-BP | 2.21 | 2.03 | 2.22 | 0.94 |
| SSA-BP | 1.85 | 1.64 | 1.51 | 0.96 |
| ISSA-BP | 1.21 | 0.93 | 1.13 | 0.99 |
5 结束语
本研究提出了一种改进的麻雀搜索算法(ISSA),并基于BP神经网络构建了AQI预测模型(ISSA-BP)。通过改进后的麻雀搜索算法来优化BP神经网络权值及阈值,与未优化的BP神经网络相比,显著提升了其预测精度,可有效预测AQI。所建立的ISSA-BP模型不仅解决了传统BP神经网络在预测AQI方面的不足,更弥补了利用麻雀搜索算法在优化模型时的缺陷。下一步研究重点是将ISSA-BP模型应用到实际工程领域中,以进一步验证其性能。
| [1] |
黄伟建, 李丹阳, 黄远. 面向空气质量的时空混合预测模型[J]. 计算机应用, 2020, 40(11): 3385-3392. |
| [2] |
刘炳春, 郑红梅, 张斌. 基于IG-LASSO模型的城市空气质量指数混合预测研究[J]. 环境科学与技术, 2017, 40(11): 144-148. |
| [3] |
杨云, 付彦丽. 关于空气中PM2.5质量浓度预测研究[J]. 计算机仿真, 2016, 33(3): 413-418. |
| [4] |
杨丰玉, 王宝英, 陈英, 等. 一种考虑风力作用的KNN城市AQI预测算法[J]. 计算机应用研究, 2019, 36(6): 1679-1682, 1722. |
| [5] |
石晓文, 蒋洪迅. 面向高精度与强鲁棒的空气质量预测LSTM模型研究[J]. 统计与决策, 2019, 35(16): 49-53. |
| [6] |
王国胜, 郭联金, 董晓清, 等. 深圳市区空气污染的人工神经网络预测[J]. 环境工程学报, 2015, 9(7): 3393-3399. |
| [7] |
张旭, 杜景林. 改进PSO-GA-BP的PM2.5浓度预测[J]. 计算机工程与设计, 2019, 40(6): 1718-1723. |
| [8] |
杨云, 杨毅. 基于GA-BP神经网络的供暖期空气质量指数预测分析[J]. 陕西科技大学学报(自然科学版), 2016, 34(4): 171-176, 186. |
| [9] |
李黄曼, 张勇, 张瑶. 基于ISSA优化SVM的变压器故障诊断研究[J]. 电子测量与仪器学报, 2021, 35(3): 123-129. |
| [10] |
毛清华, 张强. 融合柯西变异和反向学习的改进麻雀算法[J]. 计算机科学与探索, 2021, 15(6): 1155-1164. |
| [11] |
王海瑞, 鲜于建川. 改进麻雀搜索算法在分布式电源配置中的应用[J]. 计算机工程与应用, 2021, 57(20): 245-252. |
| [12] |
LIU L F, SUN S Z, YU H Y, et al. A modified Fuzzy C-Means (FCM) clustering algorithm and its application on carbonate fluid identification[J]. Journal of Applied Geophysics, 2016, 129: 28-35. |
| [13] |
张伟康, 刘升, 任春慧. 混合策略改进的麻雀搜索算法[J]. 计算机工程与应用, 2021, 57(24): 74-82. |
| [14] |
汤安迪, 韩统, 徐登武, 等. 基于混沌麻雀搜索算法的无人机航迹规划方法[J]. 计算机应用, 2021, 41(7): 2128-2136. |
| [15] |
高文欣, 刘升, 肖子雅, 等. 柯西变异和自适应权重优化的蝴蝶算法[J]. 计算机工程与应用, 2020, 56(15): 43-50. |
| [16] |
蔡恒雨, 郑启龙. 深度学习节点分配的遗传算法设计[J]. 小型微型计算机系统, 2021, 42(6): 1158-1164. |
| [17] |
钱晓宇, 方伟. 基于局部搜索的反向学习竞争粒子群优化算法[J]. 控制与决策, 2021, 36(4): 779-789. |
| [18] |
王伟, 代红, 赵斯祺. 基于特征优化和BP神经网络的入侵检测方法[J]. 计算机工程与设计, 2021, 42(10): 2755-2761. |
| [19] |
LIU Y Q, QIU D C, LI H L, et al. The intrusion detection modle utilizing LE and modified PSO-BP[C]//IEEE BEIJING SECTION. Proceedings of 2017 IEEE 8th international conference on software engineering and service science. Beijing, China: Institute of Electrical and Electronics Engineers, 2017: 318-321.
|
| [20] |
刘文杰, 邢彦锋, 陆瑶. 基于改进的BP神经网络胶铆接头的力学性能预测研究[J]. 农业装备与车辆工程, 2021, 59(3): 12-16. |



