现代通信系统自出现以来，实现更安全、更高效及更可靠的通信方式是人类一直以来追求的目标。随着信息技术的高速发展，特别是在深度学习和人工智能等领域取得的巨大进步，大大加速了云计算、无人驾驶以及车联网等新型技术的应用。同时，对通信系统也提出了更高的可靠性、更小的时延以及更大的数据带宽要求。信道编码是通信系统中的基础核心技术，(Low Density Parity Check, LDPC)译码作为优秀的信道编码方案，具有纠错性能好且易于并行译码的特点，吸引了来自国内外众多研究者的关注。LDPC码由Gallager^{[1, 2]}首次提出，但受限于当时的硬件技术水平，其译码算法难以实现，在此后的30多年间基本被研究者忽略。到20世纪90年代中后期，随着计算机及硬件技术的发展，特别是Mackay等^[3-6]开展的系列研究，重新掀起了人们对LDPC码的关注，围绕LDPC码的研究取得了大量实用的研究成果^[7-11]。由于众多研究者的努力，在2016年底，3GPP RAN1#86次会议决定将准循环LDPC码确定为5G-eMBB通信环境下大数据包(长码)的信道编码方案。

一般情况下，可以将LDPC码的译码算法分为以下3个种类^[12]：①软判决译码算法，②硬判决译码算法，③基于可靠度的译码算法。软判决译码算法主要为和积译码算法(SPA)与其改进算法，在上述算法中性能最优，但由于在算法中采用浮点数乘法以及对数运算，其计算复杂度非常高。早期的硬判决算法主要有Gallager教授^[1]的比特翻转(BF)译码算法，以及Lin等^[13]提出的一步大数逻辑译码(OSMLGD)算法。其中BF译码算法的核心思想为采用该比特参与运算的校验和进行判断是否翻转该位，而OSMLGD是首个类MLGD译码算法，两者的计算复杂度都极低，由于采用信道的硬判决信息进行译码，译码信息损失较大，所以译码性能较差。最近，Liu等^[14]通过引入比特位自适应阈值门限策略，避免了全局最大值搜索处理，实现了高吞吐量、低时延的BF译码算法，特别适合硬件实现。硬判决与软判决译码算法均存在明显的优缺点，研究者们结合两类算法的特点展开研究，提出了一类基于可靠度的译码算法，实现了性能与复杂度之间的均衡。例如，Huang等^[15]提出基于可靠度的迭代大数逻辑译码(RBI-MLGD)算法，该算法对初始信道信息进行量化处理，作为信道信息的可靠度量，在译码迭代过程中，通过在校验节点获取外信息对变量节点的可靠度信息进行更新处理，结合大数逻辑的处理策略实现译码性能的提升。此外，Chen等^[16]在RBI-MLGD算法的基础上提出了改进的译码(MRBI-MLGD)算法，该算法的核心思想是在迭代译码信息更新过程中引入修正系数，同时，只在初始信道信息的基础上进行信息更新处理，提高了译码信息的迭代更新效率，以此实现了译码性能的提升。由于MLGD类算法具有低复杂度、低时延的特点，研究者一直对其开展相关研究。最近，Song等^[17]针对多元LDPC译码算法，基于软可靠度迭代IISRB-MLGD译码算法，提出了一种裁剪的CM-IISRB译码算法。该算法采用非饱和截切策略，在较低复杂度的情况下，实现了更优的译码性能。

在MRBI-MLGD译码算法中，由于引入了缩放因子，即采用了乘法修正系数，不可避免地增加了大量的浮点数乘法运算，其译码复杂度随着迭代次数的递增而明显增大。受MRBI-MLGD算法在译码迭代过程中引入缩放因子的启发，本文提出了一种基于量化修正的低复杂度LDPC译码算法，该算法在对信道信息预处理时引入量化信息修正处理策略，从而避免在译码迭代过程中进行译码信息修正处理操作，在保持译码性能的同时，较大幅度地降低了译码复杂度。基于上述算法思想，针对均匀和非均匀量化方案，本文具体实现了基于修正系数的均匀量化和基于列重信息修正的非均匀量化两种译码方案设计，期望所提出的译码方案在降低译码复杂度的同时，还能保持一定的译码性能。

1 数字通信模型及相关定义

定义H=[h_{i, j}]_m×n(h_{i, j}∈ $\mathbb{F}_{2}$)为一个稀疏矩阵，如矩阵H具有恒定的行重ρ，即每行非零元素个数，恒定的列重γ，即每列非零元素个数，则定义为规则LDPC码。为方便接下来对本文算法进行描述，定义以下两个集合: ①定义矩阵H中第i行非零列下标集合N_i={j: 0≤j≤n-1, h_ij≠0}；②定义矩阵H中第j列非零行下标集合M_j={i: 0≤i≤m-1, h_ij≠0}。设传输的信息序列为u= u₀, u₁, …, u_k-1，u ∈$\mathbb{F}$₂^k。经过LDPC编码后可以得到码字序列c= c₀, c₁, …, c_n-1，c∈$\mathbb{F}$₂ⁿ，其中，满足cH^T =0。接下来对获得的LDPC码字序列c进行调制，获得发送的实数信号序列x = x₀, x₁, …, x_n-1，可采用BPSK进行调制，本文具体实现方法为x_j=1-2c_j。然后，把信号序列x经过加性高斯白噪声信道(AWGN)进行传输，在接收端即可获得一个接收信号序列y = y₀, y₁, …, y_n-1，该序列由发送信号叠加一个高斯白噪声信号，可以表示为y_j=x_j+n_j，其中，n_j为高斯白噪声，且满足n_j~N(0，σ²)。

2 MRBI-MLGD算法描述

在接收端获得信号序列y=(y₀, y₁, …, y_n-1)，将其进行量化处理后获得量化序列q=(q₀, q₁, …, q_n-1)，即为来自信道的初始可靠度信息序列，令R_j⁽⁰⁾=q_j，其中，设量化函数为Q(y_j)=q_j。通过量化序列q，可计算获得其硬判决码字序列z=(z₀, z₁, …, z_n-1)，具体计算方法如下：

$ z_{j}=\left\{\begin{array}{l} 0, R_{j}^{(k)} \geqslant 0 \\ 1, R_{j}^{(k)}<0 \end{array}, \right. $

(1)

在获得硬判决序列z后，可以计算其相应的校验伴随式s= zH^T，其中，s=(s₀, s₁, …, s_n-1)，实现计算方法如下：

$ s_{i}^{(k)}=\sum\nolimits_{0 \leqslant j \leqslant n-1} \oplus z_{i}^{(k)} h_{i, j}, $

(2)

式中，h_{i, j}为校验矩阵H中的元素，符号⊕为模2加运算，上标k表示第k次迭代。如s=0则表示当前判决码字校验成功，可输出码字序列z=(z₀, z₁, …, z_n-1)；如s≠0则表明校验失败，继续进入迭代译码过程。接下来对具体的迭代译码过程进行描述。

① 计算外信息。

在迭代过程中，译码算法在校验节点C_i中计算外信息σ_{i, j}^(k)，同时，将该外信息传递至其对应的变量节点V_j。校验节点C_i传递至变量节点V_j的外信息σ_{i, j}^(k)计算方法如下：

$ \sigma_{i, j}^{(k)}=\sum\limits_{j^{\prime} \in N_{i \backslash j}} \bigoplus z_{j^{\prime}}^{(k)} h_{i, j}, $

(3)

式中，符号N_i\j表示除了当前j列的其他列的序号集合。

②计算总外信息。

经过上述计算后，变量节点V_j即可获得所有校验节点的外信息σ_{i, j}^(k)，在变量节点V_j，可计算该变量节点的总外信息ε(k)_j，其计算方法如下：

$ \varepsilon_{j}^{(k)}=\sum\limits_{i \in M_{j}}\left(1-2 \sigma_{i, j}^{(k)}\right) 。$

(4)

③ 更新可靠度。

设在译码迭代过程中，设R_j^(k)为第k次迭代时变量节点V_j的当前可靠度信息，其信息更新策略如下：

$ R_{j}^{(k+1)}=R_{j}^{(0)}+\alpha \cdot \varepsilon_{j}^{(k)}, $

(5)

式中，α为译码信息修正系数。从式(5)可以看出，变量节点的信息处理方法是在初始的信道信息R_j⁽⁰⁾基础上进行更新，这种处理机制对迭代系统的稳定性有帮助。此外，由于引入了修正系数，MRBI-MLGD译码算法在收敛速度和译码性能方面，相较于原RBI-MLGD译码算法均获得明显提升。

3 基于量化修正的译码算法设计

在上述MRBI-MLGD算法中，变量节点信息更新函数为R_j^(k+1)=R_j⁽⁰⁾+α·ε_j^(k)，通过数值分析发现，ε_j^(k)信息为所有来自相连接校验节点的外信息之和，校验节点的外信息为二值的，ε_j^(k)值的大小与LDPC码的列重相关。而算法为保持一定的稳定性，采用了在R_j⁽⁰⁾的基础上进行信息修正。因此，对外信息和ε_j^(k)采用α系数进行修正，以此达到变量节点合适的信息修正。α值一般通过在一定的信噪比范围内仿真搜索出性能表现最好的值。而在原始的RBI-MLGD译码算法中，在对变量节点译码信息更新时，每一个来自校验节点的外信息修正值为±1，在不进行任何信息修正时，其总外信息绝对值最大为列重γ。一般为了获取高译码性能，在算法中将量化比特b设为8 bits，则信道信息的量化值一般远大于更新修正值，在此条件下，要想实现信息的正确修正，需要更多的迭代次数。基于此，改进算法MRBI-MLGD中通过引入缩放因子α，实现了收敛速度的增长和译码性能的提升。该改进算法由于在迭代过程中引入了乘法运算，使得计算复杂度大大提升。

基于以上分析，为降低译码复杂度，本文提出了通过在信道信息初始预处理时引入量化修正处理，在迭代过程中不再使用信息修正操作，实现译码复杂度的降低。针对均匀和非均匀量化方案，本文提出了两种量化修正方案，一种为基于修正系数的均匀量化译码方法，具体地，该方法通过在量化函数中引进修正系数，避免在译码迭代中引进浮点乘法运算，在保持译码性能的前提下，实现了译码迭代过程中计算复杂度的明显下降；另一种为基于列重γ与量化比特b的改进型非均匀量化方案，在对3-4 bits极低量化比特的情况下，也能保持较优秀的译码性能，同时，其算法复杂度和硬件资源消耗也大为降低，该方案可用于硬件资源遭受限制的场景。

3.1 基于修正系数的均匀量化及译码方案设计

由译码判决信息规则和量化原理可知，在不改变信道信息可靠度极性的情况下，不会影响LDPC码字的判决，因此，可以对可靠度值进行缩放处理。为了避免在迭代译码过程中引入乘法修正运算，降低迭代译码过程的计算复杂度，本文提出的算法1为在对信道信息量化预处理时引入修正系数β，对量化值进行预修正处理。具体计算方法如下：

$ q_{j}=\left\{\begin{array}{l} +\beta\left(2^{b}-1\right), y_{j} \geqslant\left(2^{b}-1\right) {\mathit{\Delta}} \\ \beta\left[\frac{y_{j}}{\mathit{\Delta}}\right], \left|y_{j}\right|<\left(2^{b}-1\right) {\mathit{\Delta}} \\ -\beta\left(2^{b}-1\right), y_{j} \leqslant-\left(2^{b}-1\right) {\mathit{\Delta}} \end{array}\right., $

(6)

式中，b为量化比特位数，Δ为量化间隔。采用修正系数β对量化值进行修正，通过修正处理，使信道初始可靠度值与译码迭代过程中的译码信息更新在数值上相适配，从而实现更有效的译码信息更新，获得译码性能的提升。其中，β值可以通过仿真搜索获得。

此外，在MRBI-MLGD算法中变量节点信息更新策略式(5)修改如下：

$ R_{j}^{(k+1)}=R_{j}^{(0)}+\varepsilon_{j}^{(k)} $

(7)

从式(7)可以看出，相比式(5)取消了修正系数α，由于在对信道信息量化时便引入了信息修正策略，此时的初始可靠度R_j⁽⁰⁾进行了相应修正处理，与外信息和ε_j^(k)之间已做了数值上的适配，因此不需要在更新规则中引入修正系数α。相较于MRBI-MLGD，本文算法可靠度R_j^(k+1)的更新规则省掉浮点乘法运算，译码迭代过程中的浮点乘法计算量实现大幅削减。

对本文提出的算法1——基于修正系数的均匀量化方案及LDPC译码算法具体实现步骤描述如下。

步骤1:输入。

最大迭代次数I_max，接收信号向量y，修正系数β，量化参数b和Δ。

步骤2: 初始化。

按式(6)对接收信号y进行量化得到q_j，将迭代次数k置0，对0≤j≤n-1，令初始可靠度R_j⁽⁰⁾=q_j。

步骤3: 迭代过程。对k < I_max，

① 按式(1)计算硬判决序列z^(k)；

② 按式(2)计算校验和s^(k)，如果s^(k)=0，则执行步骤4；

③ 遍历0≤i≤m-1，按式(3)计算外信息σ_{i, j}^(k)；

④ 遍历0≤j≤n-1，按式(4)计算总外信息ε_j^(k)；

⑤ 遍历0≤j≤n-1，按式(7)更新可靠度R_j^(k+1)；

⑥ 迭代次数k=k+1。

步骤4:输出。

输出硬判决序列z^(k)。

3.2 基于列重修正的非均匀量化及译码方案设计

在均匀量化方案中，由于采用固定步长进行量化，因此在对接近0区域的信号进行量化时，其量化精度较粗糙，不能更精细地对信道信息进行有效表达。特别是在采用较低量化比特时，会严重影响译码性能。上述总外信息计算式(4)可以看出，每次译码迭代时，可靠度的修正幅度ε_j^(k)与列重γ相关。当取量化比特b较大，而此时列重γ较低时，则每次迭代信息的更新幅度有限，大大降低了可靠度R_j^(k+1)的更新效率。例如，量化比特b=8，此时量化数值的范围比较大，如果仅仅简单采用列重γ个单位外信息对变量节点进行修正，由于列重γ的数值与量化范围数值相差较大，通过有限的k次迭代可能无法正确改变可靠度R_j⁽⁰⁾极性，也就是无法对错误比特进行有效翻转，实现正确译码。在改进的MRBI-MLGD译码算法中，通过在可靠度更新时引入修正系数α实现与量化范围的适配，获得收敛速度和译码性能的提升。由于在译码迭代过程中引入了乘法操作，大大增加了计算复杂度。基于上述描述，本文提出的算法2为基于列重γ修正的非均匀量化预处理译码方案，目的在对信道信息预处理阶段，引入列重γ信息，实现量化值与译码方案的适配，获得收敛速度和译码性能的提升。由于常用LDPC码的列重γ的数值一般比较小，因此本设计采用低量化比特的非均匀量化方法。具体的计算方法如下：

$ \begin{array}{*{20}{l}} \;\;\;\;\;\;\;\;\;q_{j}= \\ \left\{\begin{array}{l} \theta sgn\left(y_{j}\right)\left(2^{b}-1\right), \left|y_{j}\right| \geqslant r^{0} \\ \theta {sgn}\left(y_{j}\right)\left(2^{b}-1-p\right), r^{p+1} \leqslant\left|y_{j}\right|<r^{p}, \\ \theta {sgn}\left(y_{j}\right), 0 \leqslant\left|y_{j}\right|<r^{2^{b}-2} \end{array}\right. \end{array} $

(8)

式中，$\theta=\frac{\gamma}{\left(2^{b+1}-2\right)}, p$为整数，且满足0≤p≤2^b-3，参数r决定非均匀量化特性，取值范围为0 < r < 1。其中，r的取值决定信息的量化精度，信道信息在0附近量化精度高，随着距离的加大量化精度越低。可通过合理地分配量化距离，在最小比特量化时实现译码性能的提升。该r值可通过仿真搜索获取。

本量化设计方案也是采用在量化预处理阶段对信道信息进行相应处理，因此，其译码迭代时可靠度的更新规则采用式(7)进行。

对本文提出的算法2——基于列重修正的非均匀量化及LDPC译码算法具体实现步骤描述如下。

步骤1:输入。

最大迭代次数I_max，接收信号向量y，修正系数β，量化参数b和Δ。

步骤2:初始化。

按式(8)对接收信号y进行量化得到q_j，将迭代次数k置0，对0≤j≤n-1，令初始可靠度R_j⁽⁰⁾=q_j。

步骤3 : 迭代过程。对k < I_max，

① 按式(1)计算硬判决序列z^(k)；

② 按式(2)计算校验和s^(k)，如果s^(k)=0，则执行步骤4；

③ 遍历0≤i≤m-1，按式(3)计算外信息σ_{i, j}^(k)；

④ 遍历0≤j≤n-1，按式(4)计算总外信息ε_j^(k)；

⑤ 遍历0≤j≤n-1，按式(7)更新可靠度R_j^(k+1)；

⑥ 迭代次数k=k+1。

步骤4:输出。

输出硬判决序列z^(k)。

4 译码复杂度和性能仿真分析 4.1 译码复杂度

本文提出的基于量化修正的译码算法复杂度主要由以下几个部分组成：

① 式(1)计算硬判决z^(k)时，需要进行n次逻辑运算；

② 式(2)计算校验和s^(k)时，需要mρ-1 =nγ-m次逻辑运算(其中ρ为行重，mρ=nγ为校验矩阵H的非零因子的个数)；

③ 在计算总外信息ε_j^(k)时，采用式(3)和(4)，共需要nγ-1 次加法运算和nγ次逻辑运算；

④ 最后，可靠度R_j^(k+1)更新时，采用式(7)需要n次整数加法。

同时，本文对RBI-MLGD、MRBI-MLGD及经典的SPA算法进行了复杂度分析。详细的复杂度对比情况如表 1所示。

其中，BO为二进制操作，AO为加法运算，RM为实数乘法，Log为对数运算。从表 1可以看出，本文提出的改进算法与原始的RBI-MLGD算法复杂度基本一致，本算法相比MRBI-MLGD算法，省掉了译码迭代过程中可靠度更新时的实数乘法计算，将会明显降低译码迭代过程中的复杂度。为直观地看出单次计算复杂度的数值情况，下面对具体的LDPC码单次计算复杂度进行数值计算。

表 2为$\mathbb{F}_{2}$(1 023, 781)规则循环LDPC码在不同译码算法中单次迭代计算的具体复杂度，其列重和行重均为32，码率为0.76。

表 3为$\mathbb{F}_{2}$(255, 175)规则循环LDPC码在不同译码算法中单次迭代计算的具体复杂度，其列重和行重均为16，码率为0.69。

4.2 译码性能

根据上文的算法描述，继续通过计算机仿真的方法，对提出的译码算法进行仿真实验，考察其译码性能。

实验1：实验采用基于欧式几何方法构造的$\mathbb{F}_{2}$(1 023, 781)规则循环LDPC码^[18]进行仿真实验，其仿真参数采用以下设置：①对均匀量化，量化比特b=8 bit，量化间隔Δ=0.015 6；②对MRBI-MLGD译码算法，设置缩放因子α=3.1；③对算法1，设置修正系数β=0.322 58；④对算法2采用非均匀量化，设置量化比特b=4 bit，r=0.88。所有算法中，最大仿真迭代次数均设置为I_max=30。译码BER性能仿真曲线如图 1所示。

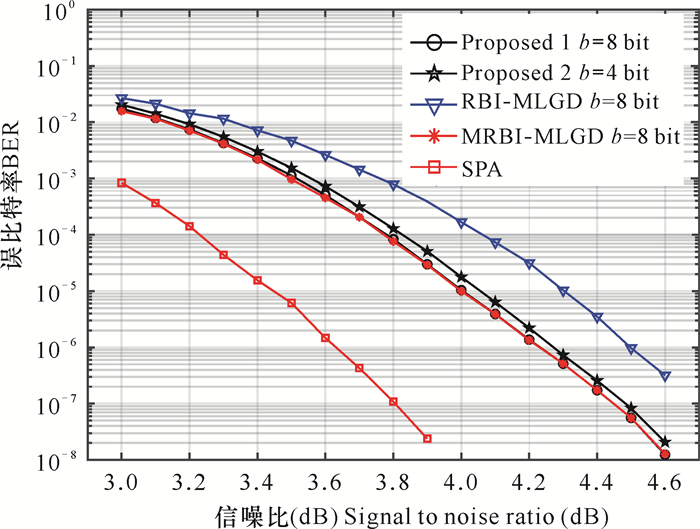
从图 1可以看出，在中高信噪比区域，算法1与MRBI-MLGD算法拥有几乎相同的译码性能，而相较于RBI-MLGD算法具有约0.3 dB的性能增益，与SPA译码算法仅有约0.6 dB的译码性能差距；算法2由于采用了较低的量化比特，译码性能稍差于算法1，但仍然明显优于RBI-MLGD算法。

图 2显示了对$\mathbb{F}_{2}$(1 032, 781) LDPC码进行译码的平均迭代次数，在中高信噪比区域，本文算法均有着与MRBI-MLGD算法一致的迭代收敛速度，且收敛速度明显优于RBI-MLGD算法。

实验2：实验采用$\mathbb{F}_{2}$(255, 175)规则循环LDPC码^[18]进行仿真实验，其仿真参数采用以下设置：①对均匀量化，量化比特b=8 bit，量化间隔Δ=0.015 6；②对MRBI-MLGD译码算法，设置修正系数α=7.0；③对算法1，设置修正系数β=0.143；④对算法2采用非均匀量化，设置量化比特b=4 bit，r=0.88。所有算法中，最大仿真迭代次数均设置为I_max=30。译码BER性能仿真曲线如图 3所示。

从译码性能曲线(图 3)可以看出，算法1在中信噪比范围区间与MRBI-MLGD算法几乎具有相同的译码性能，同时优于RBI-MLGD译码算法近0.4 dB的译码性能。与SPA译码算法具有约0.7 dB的性能差距；算法2在量化比特b=4 bit的情况下，仍实现了与MRBI-MLGD算法几乎相近的译码性能，同时，与SPA算法有约0.7 dB的性能差距。而在高信噪比区域，本文算法仍具有较优异的译码性能，出现了译码性能曲线明显优于MRBI-MLGD算法的趋势。

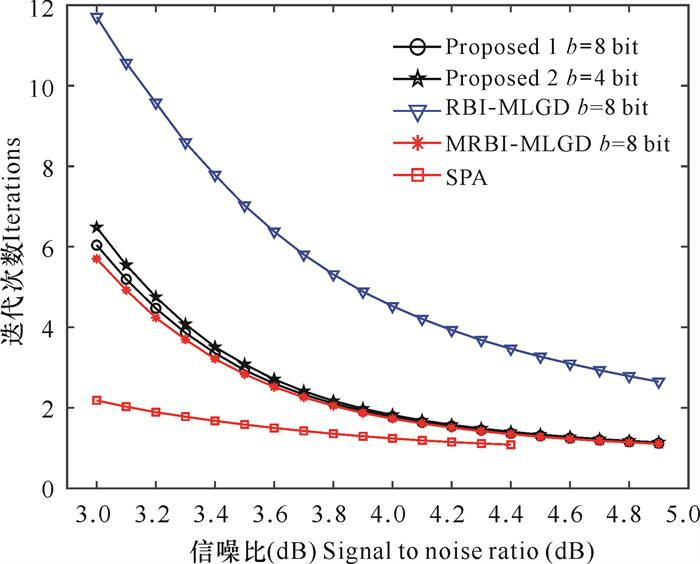
从译码平均迭代次数曲线(图 4)可以看出，算法1的译码迭代收敛速度明显高于RBI-MLGD译码算法，与MRBI-MLGD算法保持了一致的迭代收敛速度。此外，在较高信噪比时，其译码收敛速度几乎接近SPA算法。算法2在量化比特较低的情况下，仍然实现了较高的译码收敛速度，收敛速度性能与算法1一致。

5 结束语

本文在对信道信息进行量化预处理时，通过引入量化修正的信息处理策略，提出了基于量化修正的低复杂度LDPC译码算法。该算法避免了在译码迭代过程中进行信息修正处理操作，较大幅度地降低了译码复杂度，同时保持了较好的译码性能。本文具体实现了算法1为一种基于修正系数的均匀量化方案及译码算法设计；算法2为一种基于列重修正的非均匀量化方案及译码算法设计。其中，算法1通过在信道信息量化预处理时，在量化函数中引入修正系数，避免在译码迭代中的浮点乘法运算，实现了译码迭代过程中计算复杂度的明显下降；算法2通过在非均匀量化预处理时引入列重γ信息，实现了信道信息量化可靠度值与列重γ相适配的比拟关系，在迭代过程中获得更高效的译码信息传递和更新。仿真结果表明，在保持译码性能的情况下，本设计有效地降低了译码复杂度。