2. 广西民族大学,网络通信工程重点实验室,广西南宁 530006;
3. 广西混杂计算与集成电路设计分析重点实验室,广西南宁 530006
2. Key Laboratory of Network Communication Engineering, Guangxi University for Nationalities, Nanning, Guangxi, 530006, China;
3. Guangxi Key Laboratory of Hybrid Computation and IC Design Analysis, Nanning, Guangxi, 530006, China
随着现代信息技术的发展,生活中充斥着海量的数据信息,如医疗数据信息、个人消费记录、个人理财记录等,而数据信息的增多,也促使数据挖掘技术不断提高。聚类算法是数据挖掘的关键技术之一。聚类算法是根据数据之间的相似性将数据集样本划分为不同的类簇,每个类簇之间的数据相似性较高,不同的类簇中数据相似性较低。
传统的聚类算法分为基于划分的聚类算法、基于层次的聚类算法、基于密度的聚类算法、基于网格的聚类算法以及基于模型的聚类算法[1]。基于密度的聚类算法,如基于密度的噪声应用空间聚类(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)算法,其对噪声不敏感,能够发现任意形状的簇,但是该算法对参数ε和Minpts设置敏感,且对于密度不均匀的数据集,该算法不适用[2]。基于密度的聚类算法是以数据集在空间分布上的稠密度为依据进行聚类,无需预先设定类簇数,适合对未知内容的数据集进行聚类。
本文所研究的密度峰值聚类(Clustering by Fast Search and Find of Density Peaks, DPC)算法是2014年意大利学者Rodriguez等[3]提出的。DPC算法由于参数唯一、可以发现任意形状的数据、聚类过程简洁高效等优点,受到各界的广泛关注。目前,DPC算法已经在医学图像处理[4]、分子动力学[5]、文档处理[6, 7]、社区检测[8-10]等许多领域中展现出较好的性能。如在生物医学应用方面,为了确定在300 K基准温度下T-REMD模拟过程中采样的主要构象,Kührová等[11]引入了DPC算法,与εRMSD结合,提出了新的算法;Chen等[12]引入DPC算法来识别疾病症状,再利用Apriori算法分别对疾病诊断规则和疾病治疗规则进行关联分析。本文对DPC算法原理进行介绍、分析,并对自适应DPC算法的国内外研究现状进行比较总结,最后给出今后的研究方向。
1 DPC算法原理DPC算法[3]基于以下假设:每一类簇的聚类中心被与其相邻的密度较低的样本点所包围, 这些相邻的样本点距离其他局部密度相对较大的点较远。
设有数据集D={q1, q2, …, qn},对于每一点qi,由公式(1)计算其局部密度ρi,对于小规模数据集,采用公式(2)计算:
| $ \begin{align} & \ \ \ \ \ \ \ {{\mathit{\rho }}_{i}}=\sum\nolimits_{j}{\chi }\left( {{d}_{ij}}-{{d}_{c}} \right),\text{ 其中, }\chi (x)= \\ & \left\{ \begin{array}{*{35}{l}} 1, x<0 \\ 0, \text{otherwise} \\ \end{array} \right., \\ \end{align} $ | (1) |
| $ \rho_{i}=\sum\nolimits_{j} \exp \left(-\frac{d_{i j}^{2}}{d_{c}^{2}}\right),$ | (2) |
式中,dc是截断距离,dij是点qi到点qj之间的欧氏距离。
再由公式(3)计算样本点qi的距离δi,δi是样本点qi到其他密度较高样本点之间的最短距离,若qi是密度最高的样本点,则δi为qi到其他样本的最大距离。
| $ \delta_{i}=\left\{\begin{array}{l} \min\limits_{j}\left(d_{i j}\right), \rho_{j}>\rho_{i} \\ \max\limits_{j}\left(d_{i j}\right), \text { 其他 } \end{array}\right.。$ | (3) |
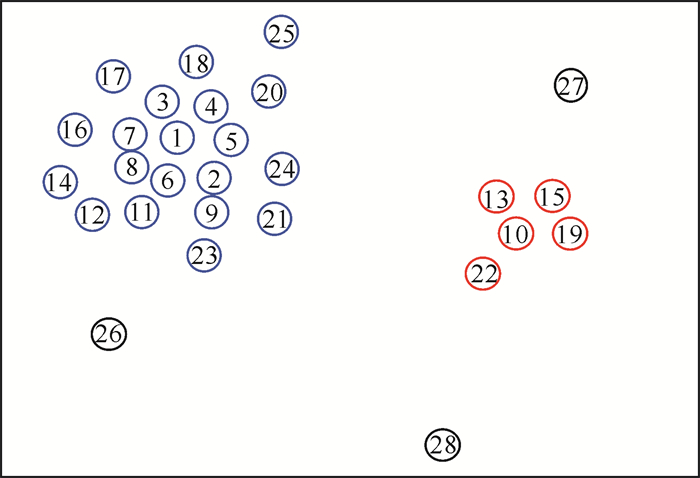
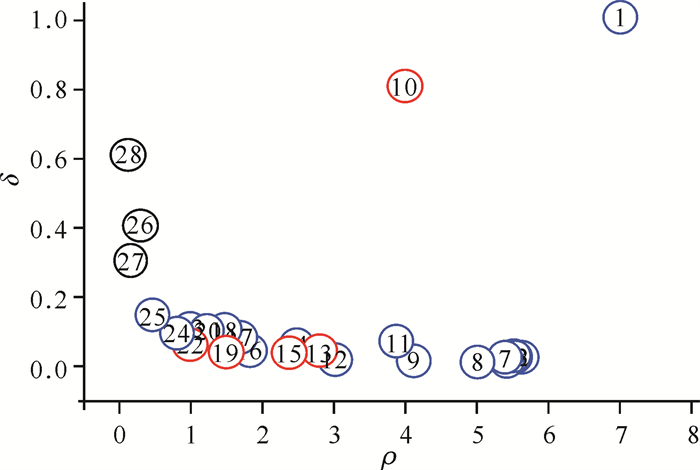
计算出qi的局部密度和距离后,选取聚类中心。在DPC算法中,选取聚类中心的方法有两种,一种是决策图法,另一种是公式法。决策图法是根据样本点的局部密度和距离生成一个决策图,然后选取最佳的聚类中心点。例如,图 1中的数据点按密度递减的顺序排列,图 2是根据图 1中的样本点计算局部密度和距离后得出的决策图[3]。由此可以得出DPC算法决策图选取聚类中心的一般规律:①位于决策图右上方的样本点适合选取为聚类中心,这些点拥有较高的局部密度且距离其他更高密度的点较远;②位于决策图ρ坐标轴附近的样本点具有较近的距离,认为是普通样本点,因为其附近存在更适合选取为聚类中心的样本点;③位于决策图δ坐标轴附近且距离ρ坐标轴相对较远的样本点识别为离群点,这些点拥有较低的密度且距离更高密度点较远。
|
| 图 1 数据分布图 Fig. 1 Distribution map of data |
|
| 图 2 决策图 Fig. 2 Graph of decision |
DPC算法中选取聚类中心的另一种方法是公式法,根据公式(4)计算γ的值,并将其值进行降序排序,选取前k个样本作为聚类中心(k为预先指定的簇数)。将局部密度值与距离相乘是为了寻找局部密度较高且距离较远的样本点。但是,该公式未考虑样本点邻域结构的影响。
| $ \gamma_{i}=\rho_{i} \times \delta_{i} 。$ | (4) |
选出聚类中心后,将剩余样本点分配到距离其最近且拥有较高密度的样本点所在的类簇。
DPC算法的具体流程如算法1所示:
算法1 密度峰值聚类算法流程
输入:数据集D=q1, q2, …, qn,簇数k
输出:聚类划分结果
1.根据数据集样本点总数确定截断距离dc
2.根据公式(1)或(2)计算样本局部密度ρ
3.根据公式(3)计算样本距离δ
4.由计算出的局部密度和距离生成决策图,根据决策图或公式(4)选取聚类中心
5.将剩余样本点分配到距离其最近的局部密度较高点所在的类簇中
6.返回聚类划分结果图
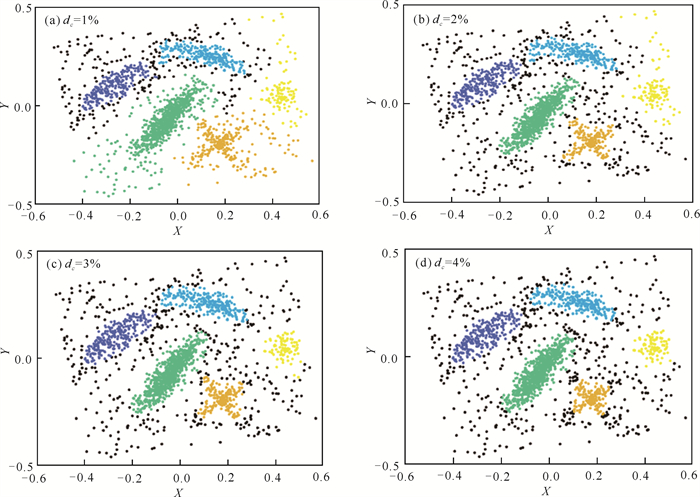
在DPC算法中,截断距离dc并不是算法自动设定的,而是按照文献[3]中提出的经验策略设定dc的值使得邻域样本点数为总样本点数的1%-2%。而在实际应用中,按照文献[3]中所提的方法设定截断距离的值,并不是所有的聚类问题都适用。图 3所示是DPC算法在不同的dc取值下对同一数据集进行聚类的结果。由图 3可以看出,虽然对类簇数没有影响,但是普通样本点和异常点的划分随着dc的取值变化而发生变化。
|
| 图 3 不同dc取值下的聚类结果 Fig. 3 Clustering results when takes different values |
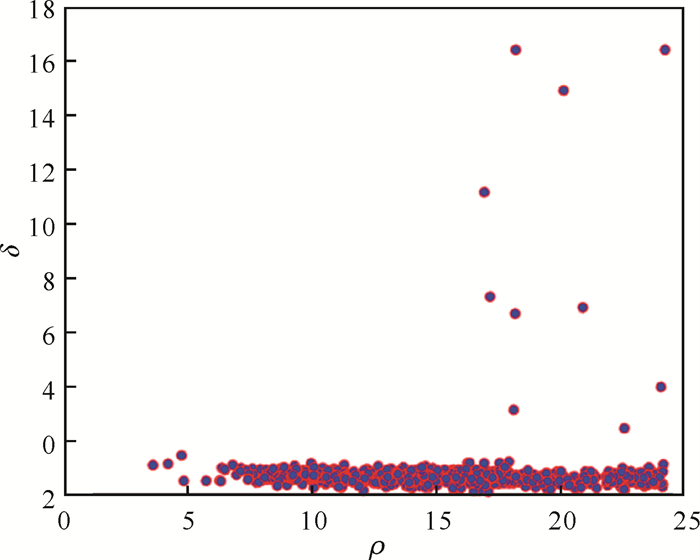
在聚类中心选取阶段,虽然根据决策图选取聚类中心能够得到较好的聚类结果,但是若数据集较为复杂,人工难以选取合适的聚类中心,而聚类中心一旦选择错误,会导致非聚类中心点分配错误。图 4为DPC算法对数据集Aggregation进行聚类时生成的决策图。由图 4可以看出,符合聚类中心要求的点不容易确定,手动选取易造成聚类中心个数选取错误。由于DPC算法聚类无需迭代,若聚类中心选取错误,会引起剩余样本点分配出现错误,最终导致聚类效果不佳。
|
| 图 4 对Aggregation数据集聚类的决策图 Fig. 4 Decision graph of aggregation data set |
目前,针对DPC算法过程不能实现自适应的问题,主要的改进方法有3种:①针对参数dc的改进,使得dc值能够自适应选取;②对计算局部密度ρ和距离δ的公式进行改进,避免参数dc的使用;③在选取聚类中心时,采用不同的方式使得聚类中心自适应选取,不需要人为参与。
2.1 参数dc的改进第1种改进方式主要是针对参数dc的选取。由于原来的dc值是人为设定的,淦文燕等[13]提出了Improved Clustering Algorithm that Searches and Finds Density Peaks (ICADEP)算法。该算法引入密度估计熵,提出新的参数优化方法,使得参数dc能够自适应选取最优值且聚类结果与核函数的类型无关,达到了更精确的聚类效果。但是该方法仍然需要人为参与选取聚类中心,为了解决这一问题,有学者引入K近邻思想[14-16],即在聚类过程中计算样本点的近邻密度,提出新的计算dc的公式,实现dc的自动计算取值。Liu等[15]提出一种新的基于K近邻的计算dc的算法。该算法不仅使得dc的值自适应选择且聚类中心的选取准确、不遗漏,并能够更好地区分核心区域和边界区域。该算法的截断距离计算公式如下:
| $ d_{c}=\mu^{K}+\sqrt{\frac{1}{N-1} \sum\nolimits_{i=1}^{N}\left(\delta_{i}^{K}-\mu^{K}\right)^{2}}, $ | (5) |
| $ \mu^{K}=\frac{1}{N} \sum\nolimits_{i=1}^{N} \delta_{i}^{K}, $ | (6) |
式中,N为数据集的样本点总数,δiK为样本点i与其第K个最近邻样本点之间的距离,μK为所有点的δiK的均值。虽然引入K近邻思想能够使得截断距离dc的值自适应选取,但是其输入参数K的值需要预先给定,而如何选取合适的K值也是一个需要研究的方向。
为了避免在改进算法的过程中出现需要选取参数的问题,王洋等[17]研究发现计算点势能的方法与DPC算法中计算ρ的方法相似,认为截断距离的最优值等价于电势能计算中的影响因子σ的最优值。而基尼指数G会随σ的改变而改变,因此,将基尼指数G最小时对应的σ作为截断距离的最优值;在聚类中心的选取上,根据γ的排序图中两点间的斜率差的变化来选取聚类中心。最终,该文算法实现了DPC算法的截断距离和聚类中心的自适应选取。
有研究将智能优化算法与DPC算法结合,如朱红等[18]将果蝇优化算法与DPC算法相结合,提出了Density Peaks Clustering Based on Fruit Fly Optimization Algorithm (FOA-DPC)算法。该算法将截断距离dc以及类簇数k作为决策变量,采用果蝇优化算法进行寻优,找到最优值后,采用公式(4)计算γi的值,选取前k个点作为聚类中心,对图像进行分割。
2.2 局部密度和距离的改进第2种改进方法的主体是局部密度和距离的计算公式。DPC算法的局部密度和距离的测量是基于截断距离的值,很难得到最优的参数。谢娟英等[19]提出的K-Nearest Neighbors Optimized Clustering Algorithm by Fast search and Finding the Density Peaks (KNN-DPC)算法采用指数核函数,根据样本的K近邻信息重新定义局部密度的计算公式,使得局部密度的计算与参数dc的取值无关,更准确地发现聚类中心。但是,其聚类中心的选择仍是人机交互模式。
Liu等[20]提出了Shared-Nearest-Neighbors-based Clustering by Fast Search and Find of Density Peaks (SNN-DPC)算法。该算法提出了共享最近邻SNN和共享最近邻相似度Sim,将Sim引入局部密度的计算中,使得局部密度和距离的计算与截断距离无关,并且提出了新的剩余样本点分配方案,避免DPC算法一步分配策略易导致的“多米诺骨牌效应”的影响。从实验结果来看,SNN-DPC算法的聚类准确性得到了提高。
虽然KNN-DPC算法和SNN-DPC算法避免了参数dc对聚类结果的影响,但是对于稀疏密度相差较大的数据集,其聚类中心较难选取。因此,薛小娜等[21]提出了Improved Density Peaks Clustering Algorithm (IDPCA)。该算法在计算局部密度时引入带有相似性系数的高斯核函数,既避免了截断距离对聚类结果的影响,又使得算法适用于任意数据集。
贾露等[22]提出的Physics Improved Density Peak Clustering Algorithm (W-DPC)引入了物理学中的万有引力定律,用于重新定义局部密度的计算。样本间距离越小,吸引力越大,局部密度越大,从而易于找到高密度点和选择聚类中心,同时还引入第一宇宙速度用于处理剩余样本点。
以上4种改进算法虽然都避免了截断距离对聚类结果的影响,但是都引入了新的参数,如KNN-DPC算法、SNN-DPC算法以及IDPCA算法中都需要预先给定样本近邻K的值,而W-DPC算法需要给出扫描半径r的值。除此之外,这4种算法的聚类中心选取方面均是采用决策图法,需要人为参与。
2.3 聚类中心选取方式的改进第3种改进方式的主体是聚类中心的选取。王星等[23]提出了Fast Searching Clustering Centers Algorithm based on Linear Regression Analysis (LR-CFDP)算法,该算法利用线性回归模型和残差分析,实现了聚类中心自动选取,解决了算法聚类中心需要人机交互选择的问题,避免了主观影响。
同样是将数学理论用于DPC算法的改进,崔世琦等[24]将高斯核函数的数学性质用于DPC算法的局部密度度量优化,并在聚类中心选取时利用γ值的中位数和绝对中位差求取残差Ri,选取前r个作为潜在聚类中心,计算α显著水平下的检验临界值λi,将原来的潜在聚类中心中λi>Ri的点作为最终的聚类中心,实现了聚类中心的自适应选取,但是对于高维数据集,该算法的性能不理想。因此,江平平等[25]提出了Improved Density Peak Clustering Algorithm based on Grid (G-DPC)算法。该算法采用网格划分法将样本空间划分为均等且不相交的网格单元,聚类中心的选取依据公式(7)和(8):
| $ \rho_{C_{i}}-\mu\left(\rho_{i}\right) \geqslant 0, $ | (7) |
| $ \left(\delta_{C_{i}}-E\left(\delta_{i}\right)\right) / 2 \geqslant \sigma\left(\delta_{i}\right), $ | (8) |
若网格代表点满足这两个公式,即为所寻聚类中心点, 其中ρCi为聚类中心的网格代表点的局部密度值,μ(ρi)是所有网格代表点的局部密度均值,δCi则表示同一类簇中其他代表点与聚类中心的代表点间的最短距离,E(δi)表示所有δi的期望。该算法实现了聚类中心自适应选取。
3 自适应DPC算法指标分析 3.1 聚类准确率(ACC)准确率[26]是计算算法正确划分的样本数占总样本数的比例,如式(9)所示。准确率的取值区间为[0, 1], 其值越大,表示算法的聚类结果越接近于正确的划分。
| $ \begin{aligned} &\ \ \ \ \ \ \ \quad \mathrm{ACC}=\frac{1}{N} \sum\nolimits_{i=1}^{N} \psi\left(x_{i}^{U}, x_{i}^{V}\right) \text {, 其中, } \psi\left(x_{i}^{U}, x_{i}^{V}\right)= \\ &\left\{\begin{array}{l} 1, x_{i}^{U}=x_{i}^{V} \\ 0, x_{i}^{U} \neq x_{i}^{V} \end{array}\right., \end{aligned} $ | (9) |
式中,U=(U1, U2, …, UL)是数据集D的标准划分,V=(V1, V2, …, VL)是优化算法的聚类结果,xiU表示样本xi在U中的标签类,xiV表示样本xi在V中的标签类。
表 1为DPC算法及6种改进算法作用在UCI数据集上的聚类准确率。可以看出,KM-DPC和IDPCA算法在Seeds数据集中取得最优的聚类结果,在Segmentation数据集中表现最佳的是KM-DPC算法;在Iris数据集中,KNN-DPC和SNN-FKNN-DPC两种算法聚类结果最好;其余的3个数据集ACC值最大的均为SNN-FKNN-DPC算法。总体来说,从ACC值来看,6种改进算法均优于DPC算法,而SNN-FKNN-DPC算法则是几个数据集中聚类最优的算法。基于聚类中心自适应改进的AD-PC-WKNN和AKDP算法与原算法相比聚类性能有了一定程度的改进,但是与基于局部密度计算方式改进的其他算法相比,性能优势不够明显。
| Algorithm | Iris | Wine | Seeds | Ionosphere | Segmentation | Dermatology |
| DPC[3] | 0.887 | 0.882 | 0.900 | 0.681 | 0.684 | 0.697 |
| KNN-DPC[19] | 0.973 | 0.948 | 0.923 | 0.729 | 0.717 | 0.768 |
| KM-DPC[27] | 0.960 | 0.960 | 0.938 | 0.821 | 0.776 | 0.809 |
| IDPCA[21] | - | - | 0.938 | 0.769 | 0.767 | 0.842 |
| SNN-FKNN-DPC[28] | 0.973 | 0.978 | 0.924 | 0.858 | - | 0.867 |
| AD-PC-WKNN[29] | 0.942 | 0.917 | 0.917 | - | - | - |
| AKDP[30] | 0.954 | 0.893 | 0.922 | - | - | - |
| 注:“-”表示没有对应的数据,加粗数据表示在该数据集中的最优聚类准确率 Note:"-" indicates that there is no corresponding data, bold data indicates the optimal clustering accuracy in the data set | ||||||
3.2 Adjusted Mutual Information (AMI)
AMI[31]是基于信息论的聚类度量指标,通过互信息(Mutual information)度量两个事件集合的相关性,如式(10)所示:
| $ \begin{array}{*{20}{l}} \;\;\;\;\;\operatorname{AMI}(U, V)= \\ \frac{M u I(U, V)-E\{M u I(U, V)\}}{\max \{H(U), H(V)\}-E\{M u I(U, V)\}}, \end{array} $ | (10) |
式中,U=(U1, U2, …, UL)是数据集D的标准划分,V=(V1, V2, …, VL)是优化算法的聚类结果, MuI(U, V)表示事件U与事件V之间的互信息,如式(11)所示,互信息是一种对称度量,用于量化两个分布之间共享的统计信息。E{ MuI(U, V) }是U和V之间的期望互信息,如式(12)所示。H(U)和H(V)分别是U和V的熵。
| $ \begin{array}{*{20}{l}} \;\;\;\;\;\;\;\; \operatorname{MuI}(U, V)= \\ \sum\nolimits_{i=1}^{K} \sum\nolimits_{j=1}^{K^{\prime}} P(i, j) \log \frac{P(i, j)}{P(i) P^{\prime}(j)}, \end{array} $ | (11) |
式中,K和K′分别是标准划分U和聚类结果V中的类簇个数,
| $ \begin{array}{*{20}{l}} \;\;\;\;\;\;\;\;E\{\operatorname{MuI}(U, V)\}= \\ \sum\limits_{i=1}^{K} \sum\limits_{j=1}^{K^{\prime}} \sum\limits_{n_{i j}=\max \left(a_{i}+b_{j-N}, 0\right)}^{\min \left(a_{i}, b_{j}\right)} \frac{n_{i j}}{N} \log \left(\frac{N \cdot n_{i j}}{a_{i} b_{j}}\right) \times \\ \frac{a_{i} ! b_{j} !\left(N-a_{i}\right) !\left(N-b_{j}\right) !}{N ! n_{i j} !\left(a_{i}-c_{i j}\right) !\left(b_{j}-c_{i j}\right) !\left(N-a_{i}-b_{j}+c_{i j}\right) !}, \end{array} $ | (12) |
式中,K和K′分别为U和V中的类簇数,ai=
AMI的取值范围是[-1, 1],其值越接近1,表示算法的聚类结果越优,越接近于真实结果。
由表 2可以看出,5种改进算法的AMI值大部分都优于原始的DPC算法。Wine数据集中AMI值最优的是SNN-FKNN-DPC算法,Seeds数据集最优的是W-DPC算法,Libras movement和Waveform数据集中表现最佳的是SNN-DPC算法,Waveform(noise)数据集中KM-DPC算法取得最优的AMI值。关于Iris数据集,KNN-DPC、SNN-FKNN-DPC以及SNN-DPC这3种算法的AMI值均为0.912,原因是该数据集中的簇重叠严重,而这3种算法均是引入近邻思想,受该数据集的特殊邻域环境影响,这3种算法在Iris数据集的AMI值相等。
| Algorithm | Iris | Wine | Seeds | Libras Movement | Waveform | Waveform (noise) |
| DPC[3] | 0.767 0 | 0.706 0 | 0.717 0 | 0.390 0 | 0.318 0 | 0.184 0 |
| KNN-DPC[19] | 0.912 0 | 0.829 0 | 0.785 0 | 0.523 0 | 0.313 0 | 0.245 0 |
| SNN-FKNN-DPC[20] | 0.912 0 | 0.908 0 | 0.767 0 | 0.507 0 | 0.382 0 | 0.296 0 |
| KM-DPC[27] | 0.883 0 | 0.860 0 | 0.777 0 | 0.505 0 | 0.386 0 | 0.390 0 |
| W-DPC[22] | 0.911 5 | 0.867 8 | 0.820 9 | 0.381 0 | - | - |
| SNN-DPC[20] | 0.912 0 | 0.874 0 | 0.751 0 | 0.583 0 | 0.398 0 | 0.326 0 |
| 注:“-”表示没有对应的数据,加粗数据表示在该数据集中的最优聚类准确率 Note:"-" indicates that there is no corresponding data, bold data indicates the optimal clustering accuracy in the data set | ||||||
3.3 Adjusted Rand Index (ARI)
兰德指数(Rand Index, RI)只考虑表 3所示的a和d两种聚类结果的情况,忽略了b和c两种聚类结果,评价方式较为片面并且没有区分度,其计算公式如式(13)。其中,U=(U1, U2, …, UL)是数据集D的标准划分,V=(V1, V2, …, VL)是优化算法的聚类结果:
| $ \mathrm{RI}(U, V)=\frac{a+d}{a+b+c+d}, $ | (13) |
ARI[32]是基于RI的改进,度量标准划分U和聚类结果V之间的相似程度,如式(14),也可用式(15)来表示。ARI的取值范围为[-1, 1],数值越高表示聚类划分效果越好。
| $ \begin{array}{*{20}{l}} \;\;\;\;\operatorname{ARI}(U, V)= \\ \frac{\operatorname{RI}(U, V)-E\{\operatorname{RI}(U, V)\}}{\max \{\operatorname{RI}(U, V)\}-E\{\operatorname{RI}(U, V)\}} , \end{array} $ | (14) |
| $\begin{array}{*{20}{l}} \;\;\;\;\;\;\;\;\operatorname{ARI}(U, V)=\\ \frac{\sum\nolimits_{i, j}\left(\begin{array}{l} n_{i j} \\ 2 \end{array}\right)-\left[\sum\nolimits_{i}\left(\begin{array}{l} n_{i \cdot} \\ 2 \end{array}\right) \sum\nolimits_{j}\left(\begin{array}{l} n_{\cdot j} \\ 2 \end{array}\right)\right] /\left(\begin{array}{l} n \\ 2 \end{array}\right)}{\frac{1}{2}\left[\sum\nolimits_{i}\left(\begin{array}{l} n_{i \cdot} \\ 2 \end{array}\right)+\sum\nolimits_{j}\left(\begin{array}{l} n_{\cdot j} \\ 2 \end{array}\right)\right]-\left[\sum\nolimits_{i}\left(\begin{array}{l} n_{i \cdot} \\ 2 \end{array}\right) \sum\nolimits_{j}\left(\begin{array}{l} n_{\cdot j} \\ 2 \end{array}\right)\right] /\left(\begin{array}{l} n \\ 2 \end{array}\right)}, \end{array} $ | (15) |
式中,nij= |Ui∩Vj|为在U中属于Ui且在V中属于Vj的样本总数,ni·表示在U中属于类簇Ui的样本个数,n·j表示在V中属于类簇Vj的样本个数。
| 类型 Type |
描述 Description |
| a | 在U和V中均在同一类簇的样本对数目 The number of sample pairs in U and V are in the same class cluster |
| b | 在U中划分在同一类簇,但在V中未划分在同一类簇的样本对数目 The number of sample pairs classified in the same cluster in U, but not in the same cluster in V |
| c | 在U中未划分在同一类簇,但在V中划分在同一类簇的样本对数目 The number of sample pairs that are not classified in the same cluster in U, but are in the same cluster in V |
| d | 在U和V中均未划分在同一类簇的样本对数目 The number of sample pairs where U and V are not classified in the same cluster |
表 4是6种改进算法和DPC算法在UCI数据集的ARI值。相比于DPC算法,各改进算法在UCI数据集的ARI值均有所改善,其中,在Iris数据集中,SNN-DPC算法表现最佳;SNN-FKNN-DPC算法在Wine和Libras movement两个数据集的聚类结果相比于其他算法较优;KM-DPC算法在Seeds和Segmentation数据集的ARI值最大;在WDBC数据集中,聚类效果最优的是SNN-DPC算法。
| Algorithm | Iris | Wine | Seeds | Libras Movement | WDBC | Segmen- tation |
| DPC[3] | 0.720 | 0.672 | 0.734 | 0.214 | -0.011 | 0.550 |
| KNN-DPC[19] | 0.922 | 0.844 | 0.788 | 0.331 | 0.783 | 0.539 |
| KM-DPC[27] | 0.886 | 0.884 | 0.835 | 0.291 | 0.818 | 0.632 |
| SNN-DPC[26] | 0.922 2 | 0.899 2 | 0.789 0 | 0.392 7 | 0.850 3 | 0.577 0 |
| W-DPC[22] | 0.868 1 | 0.800 6 | 0.732 0 | 0.323 2 | 0.805 1 | - |
| SNN-FKNN- DPC[28] | 0.922 | 0.933 | 0.791 | 0.407 | - | - |
| 注:“-”表示没有对应的数据,加粗数据表示在该数据集中的最优聚类准确率 Note:"-" indicates that there is no corresponding data, bold data indicates the optimal clustering accuracy in the data set | ||||||
3.4 F-Measure
F-Measure[33]指标综合了查准率(Precision)和查全率(Recall)两种评价指标,其优势在于对聚类结果的整体区分能力。一般的聚类结果分布情况总结如表 3所示。F-Measure的取值范围为[0, 1],数值越高表示聚类效果越好。
查准率评估聚类结果的精确程度,计算方式如公式(16)所示。查全率评估实验结果的完备程度,计算方式如公式(17)所示。F-Measure的计算方式如式(18)所示。
| $ \text { precision }=\frac{a}{a+c}, $ | (16) |
| $ \text { recall }=\frac{a}{a+b}, $ | (17) |
| $ F_{\beta}=\left(1+\beta^{2}\right) \frac{\text { precision } \cdot \text { recall }}{\beta^{2} \cdot \text { precision }+\text { recall }}, $ | (18) |
在此,β=1,即
由表 5可以看出,ADPC-KNN算法在Seeds和Libras Movement两个数据集中的F-Measure值较其他算法大,即该算法在这两个数据集中的表现最佳;而在Iris、Wine、Ecoli以及WDBC 4个数据集中聚类结果最优的是SNN-DPC算法。
| Algorithm | Iris | Wine | Seeds | Libras Movement | Ecoli | WDBC |
| DPC[3] | 0.923 3 | 0.783 5 | 0.844 4 | 0.371 7 | 0.577 5 | 0.725 7 |
| KNN- DPC[19] | 0.935 5 | 0.866 7 | 0.827 6 | 0.397 6 | 0.691 9 | 0.765 8 |
| ADPC- KNN[15] | 0.900 0 | 0.720 0 | 0.920 0 | 0.500 0 | 0.640 0 | - |
| SNN- DPC[20] | 0.947 9 | 0.933 0 | 0.858 9 | 0.450 7 | 0.824 3 | 0.930 5 |
| W-DPC[22] | 0.911 5 | 0.867 8 | 0.820 9 | 0.404 0 | 0.659 2 | 0.910 0 |
| E-DPC[24] | 0.905 0 | 0.601 0 | 0.877 | - | - | - |
| 注:“-”表示没有对应的数据,加粗数据表示在该数据集中的最优聚类准确率 Note:"-" indicates that there is no corresponding data, bold data indicates the optimal clustering accuracy in the data set | ||||||
3.5 算法平均运行时间
由表 6可以看出,3种改进算法的平均运行时间均大于DPC算法,而由前面的ACC、AMI、ARI以及F-Measure 4个指标可以看出,这些算法的聚类结果都比DPC算法有所改善,但是其运行时间都比DPC算法慢。
由表 1、表 2、表 4、表 5及表 6的数据可以看出,3种方向上的改进算法相比于原来的算法,聚类性能在一定程度上都得到了提升,但是从整体上来看,针对dc值选取的改进算法以及针对聚类中心选取的改进算法,在数据集上的聚类效果不如基于局部密度计算公式的改进算法。5个表格中的数据集均为规模较小的数据集,说明已改进的算法在处理规模较小、数据分布较为均匀的数据集时聚类效果比较理想。
4 展望本文主要分析了目前针对DPC算法参数dc及其聚类中心的选取不能自适应的缺陷,研究者对其进行改进的研究工作,并对改进算法的聚类结果指标进行分析。未来可从以下3个方面进行深入研究:
① 将智能优化算法与DPC聚类算法有机结合,研究自适应DPC自动聚类算法:目前已有的对于DPC算法的自适应改进方式,主要是针对参数的自适应或者在选取聚类中心时无需人为参与,两者同时达到自适应效果的改进仍然较少,基于此,对DPC算法的自适应研究还可以更加完善;
② DPC算法参数选取的数学理论依据分析:目前参数的选取主要依赖经验策略,缺乏数学理论的支撑;
③ 高维空间DPC聚类算法理论与方法研究:虽然PDC算法能够识别任意形状簇,但是对于高维数据集,该算法的处理性能不够理想,而现有的针对高维数据的改进方式主要是基于PCA的改进算法,因此,DPC在高维空间的研究有待进一步探索。
| [1] |
JAIN A K. Data clustering: 50 years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8): 651-666. DOI:10.1016/j.patrec.2009.09.011 |
| [2] |
冯少荣, 肖文俊. DBSCAN聚类算法的研究与改进[J]. 中国矿业大学学报, 2008, 37(1): 105-111. DOI:10.3321/j.issn:1000-1964.2008.01.021 |
| [3] |
RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
| [4] |
ZENG X H, CHEN A Z, ZHOU M. Color perception algorithm of medical images using density peak based hierarchical clustering[J]. Biomedical Signal Processing and Control, 2019, 48: 69-79. DOI:10.1016/j.bspc.2018.09.013 |
| [5] |
LIU S, ZHU L Z, SHEONG F K, et al. Adaptive partitioning by local density-peaks: An efficient density-based clustering algorithm for analyzing molecular dynamics trajectories[J]. Journal of Computational Chemistry, 2017, 38(3): 152-160. DOI:10.1002/jcc.24664 |
| [6] |
ZHANG Y, XIA Y Q, LIU Y, et al. Clustering sentences with density peaks for multi-document summarization [C]// Proceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Denver, Colorado, 2015: 1262-1267.
|
| [7] |
WANG B Y, ZHANG J, DING F G, et al. Multi-document news summarization via paragraph embedding and density peak clustering [C]//2017 International Conference on Asian Language Processing (IALP), Singapore: IEEE, 2017.
|
| [8] |
WANG M M, ZUO W L, WANG Y. An improved density peaks-based clustering method for social circle discovery in social networks[J]. Neurocomputing, 2016, 179: 219-227. DOI:10.1016/j.neucom.2015.11.091 |
| [9] |
XU M L, LI Y H, LI R X, et al. EADP: An extended adaptive density peaks clustering for overlapping community detection in social networks[J]. Neurocomputing, 2019, 337: 287-302. DOI:10.1016/j.neucom.2019.01.074 |
| [10] |
LU H, SHEN Z, SANG X S, et al. Community detection method using improved density peak clustering and nonnegative matrix factorization[J]. Neurocomputing, 2020, 415: 247-257. DOI:10.1016/j.neucom.2020.07.080 |
| [11] |
KÜHROVÁ P, BEST R B, BOTTARO S, et al. Computer folding of RNA tetraloops: Identification of key force field deficiencies[J]. Journal of Chemical Theory and Computation, 2016, 12(9): 4534-4548. DOI:10.1021/acs.jctc.6b00300 |
| [12] |
CHEN J G, LI K L, RONG H G, et al. A disease diagnosis and treatment recommendation system based on big data mining and cloud computing[J]. Information Sciences, 2018, 435: 124-149. DOI:10.1016/j.ins.2018.01.001 |
| [13] |
淦文燕, 刘冲. 一种改进的搜索密度峰值的聚类算法[J]. 智能系统学报, 2017, 12(2): 229-236. |
| [14] |
蒋礼青, 张明新, 郑金龙, 等. 快速搜索与发现密度峰值聚类算法的优化研究[J]. 计算机应用研究, 2016, 33(11): 3251-3254. |
| [15] |
LIU Y H, MA Z M, YU F. Adaptive density peak clustering based on K-nearest neighbors with aggregating strategy[J]. Knowledge-Based Systems, 2017, 133: 208-220. DOI:10.1016/j.knosys.2017.07.010 |
| [16] |
罗军锋, 锁志海, 郭倩. 一种基于k近邻的密度峰值聚类算法[J]. 软件, 2019, 41(7): 185-188. DOI:10.3969/j.issn.1003-6970.2019.07.036 |
| [17] |
王洋, 张桂珠. 自动确定聚类中心的密度峰值算法[J]. 计算机工程与应用, 2018, 54(8): 137-142. |
| [18] |
朱红, 何瀚志, 方谦昊, 等. 基于改进密度峰值聚类的医学图像分割[J]. 徐州医科大学学报, 2018, 38(10): 652-658. DOI:10.3969/j.issn.1000-2065.2018.10.006 |
| [19] |
谢娟英, 高红超, 谢维信. K近邻优化的密度峰值快速搜索聚类算法[J]. 中国科学: 信息科学, 2016, 46(2): 258-280. |
| [20] |
LIU R, WANG H, YU X M. Shared-nearest-neighbor-based clustering by fast search and find of density peaks[J]. Information Sciences, 2018, 450: 200-226. DOI:10.1016/j.ins.2018.03.031 |
| [21] |
薛小娜, 高淑萍, 彭弘铭, 等. 结合K近邻的改进密度峰值聚类算法[J]. 计算机工程与应用, 2018, 54(7): 36-43. |
| [22] |
贾露, 张德生, 吕端端. 物理学优化的密度峰值聚类算法[J]. 计算机工程与应用, 2020, 56(13): 47-53. DOI:10.3778/j.issn.1002-8331.1905-0171 |
| [23] |
王星, 呙鹏程, 王玉冰, 等. 基于线性回归分析的快速搜索聚类中心算法[J]. 系统工程与电子技术, 2017, 39(11): 2614-2622. DOI:10.3969/j.issn.1001-506X.2017.11.31 |
| [24] |
崔世琦, 刘冰, 李勇. 基于SH-ESD优化的密度峰值快速搜索聚类算法[J]. 长春工业大学学报, 2020, 41(2): 149-156. |
| [25] |
江平平, 曾庆鹏. 一种基于网格划分的密度峰值聚类改进算法[J]. 计算机应用与软件, 2019, 36(8): 268-274, 280. DOI:10.3969/j.issn.1000-386x.2019.08.045 |
| [26] |
薛小娜, 高淑萍, 彭宏铭, 等. 基于K近邻和多类合并的密度峰值聚类算法[J]. 吉林大学学报(理学版), 2019, 57(1): 111-120. |
| [27] |
刘奕志, 程汝峰, 梁永全. 一种基于共享近邻的密度峰值聚类算法[J]. 计算机科学, 2018, 45(2): 125-129, 146. |
| [28] |
杨震, 王红军. 基于加权K近邻的改进密度峰值聚类算法[J]. 计算机应用研究, 2020, 37(3): 667-671. |
| [29] |
钱雪忠, 金辉. 自适应聚合策略优化的密度峰值聚类算法[J]. 计算机科学与探索, 2020, 14(4): 712-720. |
| [30] |
CARPANETO G, TOTH P. Algorithm 548: Solution of the assignment problem[J]. ACM Transactions on Mathematical Software, 1980, 6(1): 104-111. DOI:10.1145/355873.355883 |
| [31] |
VINH N X, EPPS J R, BAILEY J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance[J]. The Journal of Machine Learning Research, 2010, 11: 2837-2854. |
| [32] |
HUBERT L, ARABIE P. Comparing partitions[J]. Journal of Classification, 1985, 2(1): 193-218. DOI:10.1007/BF01908075 |
| [33] |
WANG C X, LIU L G. Feature matching using quasi-conformal maps[J]. Frontiers of Information Technology & Electronic Engineering, 2017, 18(5): 644-657. |



