2. 广西民族大学教育科学学院,广西南宁 530006;
3. 广西大学资源环境与材料学院,广西南宁 530004
2. School of Education Science, Guangxi University for Nationalities, Nanning, Guangxi, 530006, China;
3. School of Resources, Environment and Materials, Guangxi University, Nanning, Guangxi, 530004, China
焦虑是一种常见的负性情绪,对人们的认知水平、动作执行、身心健康等都存在不同程度的影响[1-3]。准确地识别和诊断出大学生的焦虑情绪,对于针对性地开展心理治疗和危机干预,预防其发展成焦虑障碍或焦虑神经症具有重要的实践价值。当前,国内外对焦虑情绪的识别与诊断,主要采用问卷调查[2]、临床访谈[3]等主观测评方法。但是,由于受到各类主观条件(如回答的真实性与被诱导性、诊断者业务水平)的限制,识别与诊断效果并不理想。
近年来,基于脑电(Electroencephalograph, EEG)信号的焦虑情绪识别与诊断方法受到越来越多的重视。EEG焦虑情绪识别过程一般分为4个步骤[4, 5]:EEG采集、滤波与预处理、特征信息提取、模式分类。其中,EEG的特征提取方法主要包括统计特征法、时域法、频域方法、时频域法、非线性动力学分析法等[6, 7],而对应的模式分类方法主要有支持向量机、K均值聚类法、决策树等[8]。但是,传统方法在很大程度上依赖于手动或固定的提取特征方式,往往会忽略一些有用信息,造成分类准确度难以提高。为了克服上述缺点,能够自动挖掘和抽取特征信息的深度学习方法被越来越多地应用于EEG情绪识别领域[9-11]。Zheng等[9]采用微分熵与深度信念网络(Deep Belief Network,DBN)相结合的深度学习模型;Alhagry等[10]采用长短期记忆网络(Long Short-Term Memory,LSTM)构建出一种端到端的神经网络,有效提高了分类准确率,但模型运算速度较差; 针对于此,Liu等[11]进一步考虑了特征表示能力,构建了一种多层特征导引胶囊网络(Multi-Level Features Guided Capsule Network,MLF-GCN), 有效加快了运算速度。总体上看,上述方法的检测准确性依然有待提高。
近几年来,卷积神经网络(Convolutional Neural Networks, CNN)能够自动学习输入样本的特征信息,不需要手动设计,还具有局部连接和权值共享等优点,有利于加快学习速度并避免过度拟合,适应性和泛化能力更强[12-14]。因此,CNN模型及其改进方案被越来越多地应用于EEG焦虑情绪识别领域。Gao等[15]采用梯度粒子群优化(Gradient-Priority Particle Swarm Optimization,GPSO)算法来执行CNN的权值优化,Li等[16]采用分层卷积神经网络(Hierarchical Convolutional Neural Networks,HCNN)来进行EEG情绪识别,获得了良好的分类效果。但上述EEG焦虑情绪识别方法基本上属于定性分类,侧重于判断被试对象是否存在焦虑情绪或焦虑等级,而对于焦虑症状的严重程度、未来产生焦虑情绪的概率等定量化问题,国内外仍缺乏相关的文献报道。
由于焦虑情绪识别的EEG信号不仅非常复杂,还具有数据量大、特征信息繁杂等特点,本研究将对卷积神经网络这类具有深层结构的深度学习方法进行改进,使其能够应用于大学生焦虑情绪定量化识别问题的研究,在确保焦虑情绪诊断准确率的基础上,解决相关的内在病理因素分析与追溯、类别不平衡等问题,为后续临床心理治疗和心理危机干预提供更详细可靠的诊断依据。
1 模型与方法采集所得的EEG信号通常是一类微弱的、强时变的非平稳非线性信号,而且还会受到强烈的外部扰动,基本上都存在“信号淹没”现象[17]。因此,必须先经过严格的预处理和滤波,才能应用于后续的建模和特征提取。同时,大约只有1/4的高校大学生会出现不同程度的焦虑情绪,即被试样本集存在一定程度的“类别不平衡”问题[18, 19]。上述的两个困难对基于EEG信号的大学生焦虑诊断问题带来了很大的挑战。针对于此,本研究采用的技术路线如下:首先,对所采集的EEG信号进行多级混合滤波,获得可用于深度学习模型的有效EEG信号;其次,提出并构建一个基于“扩展信息输入空间[20, 21]”的神经网络(Neural Network Based on Extended Information Input Space,NN-EIIS)模型,取代末端的Softmax分类器,将传统CNN模型改进为一种具备定量逼近学习能力的卷积神经网络(Convolutional Neural Networks with Quantitative Approximation Learning, CNN-QAL);再次,引入具有独立性的焦虑量表得分(Score of Anxiety Scale,SAS)作为大学生焦虑情绪量化的标准,并应用于CNN-QAL模型训练的样本输出,获得对应的建模结果和定量分析结果;最后,根据所构建的CNN-QAL模型和定量分析结果,初步探讨和追溯内在病理因素(图 1)。
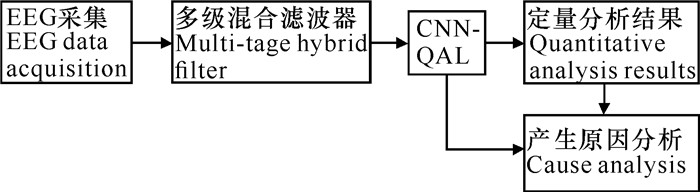
|
| 图 1 技术路线 Fig. 1 Technical route |
1.1 基于ICA的多级混合滤波器设计
由于采集的EEG信号是一种复杂的非平稳非线性信号,而且有效的EEG信号往往淹没在心电、眼电等信号之中[4, 17], 导致常规的、单一的滤波和数据预处理算法不再适用于EEG信号的滤波和预处理过程。本研究设计了一种基于独立分量分析(Independent Component Analysis, ICA)的多级混合滤波策略,具体处理过程如下:
① 前处理阶段。采用MATLAB的EEGlab模块,依次进行电极定位、重参考设置。
② 带通滤波。采用Bessel带通滤波器进行滤波,其中,滤波频带设置为[0.5, 45],能够完全覆盖影响焦虑特征信息的分布频带(1-40 Hz)。
③ ICA滤波。运用ICA算法[22]对上述EEG信号进行盲源分离。对比已知扰动噪声(如眨眼、心电信号、电极移动、头部肌肉抖动等)的时频特性,并参考文献[2, 4, 7]的处理方法,将各种干扰噪声滤除,再将信号恢复重构,得到只包含有效信息的EEG信号。
1.2 CNN-QAL模型卷积神经网络作为一种最受欢迎的深度学习算法,被广泛应用于图像处理等领域[23, 24],通过多层卷积和池化处理来自动提取输入信号的各种特征,再通过末端的全连接层和分类器来获得预期的分类结果。然而,对于焦虑情绪诊断与治疗问题来说,仅仅判断患者是否存在焦虑情绪或者进行简单的分类,对后期的临床心理治疗或心理危机干预远远不够,实际心理诊疗过程更需要进行精确的定量分析,以及对病理因素进行合理的追溯分析。鉴于此,本研究对现有CNN模型进行改进,提出一种具备定量逼近学习能力的改进卷积神经网络。经典CNN模型的总体模型表达式如下[13, 14]:
| $ \begin{array}{l} y* = Tanh\left( {FC} \right.\left( {Flat\left( {Pool\left( {Re\left( {Conv} \right.} \right.} \right.} \right.\\ \left. {\left. {\left. {\left. {\left. {\left( x \right)} \right)} \right)} \right)} \right)} \right)。\end{array} $ | (1) |
由图 2可知,常规CNN模型通常由两部分组成:前端进行特征自动提取和处理,主要包括一个输入层、若干个“卷积-池化”层,相关的网络结构设置、正向输出、反向权值调整等算法已经比较完善[13, 14],可以直接应用于基于EEG的大学生焦虑情绪识别过程;而末端负责模式分类,主要包括全连接层和输出层,一般只能进行二分类(如判断焦虑情绪“存在”或“不存在”)或有限的等级分类(如判断焦虑情绪程度“低”“中”“高”),这无法满足实际心理诊疗的要求。因此,本研究构造一个基于“扩展信息输入空间”的神经网络模型[21, 25](图 3)。

|
| 图 2 经典CNN模型的组成结构示意图 Fig. 2 Schematic diagram of the composition structure of the classic CNN model |
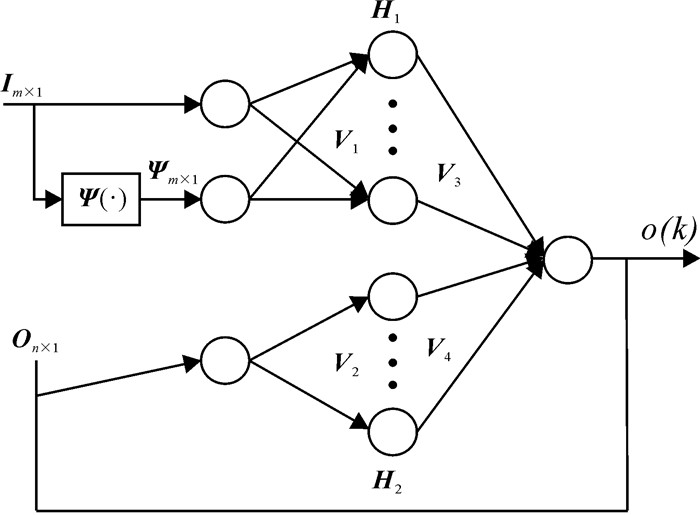
|
| 图 3 基于“扩展信息输入空间”的神经网络模型结构示意图 Fig. 3 Schematic diagram of neural network structure based on extended information input space |
图 3中Im×1,Ψm×1和On×1分别表示前端“卷积-池化”部分所自动提取的特征信息、所提取的特征经过预处理或演化后的信息、与输出相关的演化信息,这3类信息共同构成了NN-EIIS模型的“扩展信息输入空间”,可以更充分、完整地描述EEG与大学生焦虑情感之间的函数映射关系。m和n分别表示相应的信息演化处理次数;o(k)是模型的输出空间,结合实际心理诊疗的要求,本研究选择被试对象的焦虑量表得分作为模型输出;Vi(i=1,…,4)为权值向量,H表示隐藏层。如果拓展后的信息输入空间[I,Ψ,O]具有完备性,NN-EIIS模型就能够通过网络训练来无限逼近系统输出[20],从而实现高精度的EEG焦虑情绪定量识别。
为了获得更好的建模效果和提高建模精度,H1的激活函数σ1(·)选择为双曲正切函数,而H2的激活函数σ2(·)则采用线性函数,于是,所构建NN-EIIS模型的正向输出为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;o\left( k \right) = \mathit{\boldsymbol{V}}_3^T\cdot{\sigma _1}\left( {\mathit{\boldsymbol{V}}_1^T\cdot\mathit{\boldsymbol{X}} + {\theta _1}} \right) + {\rm{ }}\mathit{\boldsymbol{V}}_4^T\cdot{\sigma _2}\left( {\mathit{\boldsymbol{V}}_2^T\cdot\mathit{\boldsymbol{O}} + } \right.\\ \left. {{\theta _2}} \right) + {\theta _3}, \end{array} $ | (2) |
式中,θi(i=1,…,3)是阀值偏置。
借鉴BP神经网络的推导方法,获得相应的反向权值调整算法,若定义代价函数E和参数ξ分别为
| $ E = \frac{1}{2}\sum\limits_{k = 1}^L {{{\left( {{o_p}\left( k \right) - o\left( k \right)} \right)}^2}} = \frac{1}{2}\sum\limits_{k = 1}^L {{{\left( {e\left( k \right)} \right)}^2}} , $ | (3) |
| $ \xi = \frac{{\partial E\left( k \right)}}{{\partial o\left( k \right)}} = - \left( {{o_p}\left( k \right) - o\left( k \right)} \right) = - e\left( k \right), $ | (4) |
式(3)和式(4)中,op(k)是与EEG信号完全独立的被试对象焦虑量表得分(SAS),L为数据长度,则有
| $ \begin{array}{l} \;\;\;\;\;\;\;\frac{{\partial E\left( k \right)}}{{\partial {\mathit{\boldsymbol{V}}_3}}} = \frac{{\partial E\left( k \right)}}{{\partial o\left( k \right)}}\mathit{\boldsymbol{\cdot}}\frac{{\partial o\left( k \right)}}{{\partial {\mathit{\boldsymbol{V}}_3}}}{\rm{ = }}\\ \xi \mathit{\boldsymbol{\cdot}}{\sigma _1}\left( {\mathit{\boldsymbol{V}}_1^{\rm{T}}\mathit{\boldsymbol{\cdot X}} + {\theta _1}} \right), \end{array} $ | (5) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\frac{{\partial E\left( k \right)}}{{\partial {\mathit{\boldsymbol{V}}_4}}} = \frac{{\partial E\left( k \right)}}{{\partial o\left( k \right)}}\mathit{\boldsymbol{\cdot}}\frac{{\partial o\left( k \right)}}{{\partial {\mathit{\boldsymbol{V}}_4}}}{\rm{ = }}\\ \xi \mathit{\boldsymbol{\cdot}}{\sigma _2}\left( {\mathit{\boldsymbol{V}}_2^{\rm{T}}\mathit{\boldsymbol{\cdot X}} + {\theta _1}} \right), \end{array} $ | (6) |
| $ \frac{{\partial E\left( k \right)}}{{\partial {\theta _3}}} = \frac{{\partial E\left( k \right)}}{{\partial o\left( k \right)}}\mathit{\boldsymbol{\cdot}}\frac{{\partial o\left( k \right)}}{{\partial {\theta _3}}}{\rm{ = }}\xi , $ | (7) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\frac{{\partial E\left( k \right)}}{{\partial {\mathit{\boldsymbol{V}}_1}}} = \frac{{\partial E\left( k \right)}}{{\partial o\left( k \right)}}\mathit{\boldsymbol{\cdot}}\frac{{\partial o\left( k \right)}}{{\partial {\mathit{\boldsymbol{V}}_1}}}{\rm{ = }}\\ \xi \mathit{\boldsymbol{\cdot V}}_3^{\rm{T}}\mathit{\boldsymbol{\cdot}}{{\sigma '}_1}\left( {\mathit{\boldsymbol{V}}_1^{\rm{T}}\mathit{\boldsymbol{\cdot X}} + {\theta _1}} \right)\mathit{\boldsymbol{\cdot X}}, \end{array} $ | (8) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\frac{{\partial E\left( k \right)}}{{\partial {\theta _1}}} = \frac{{\partial E\left( k \right)}}{{\partial o\left( k \right)}}\mathit{\boldsymbol{\cdot}}\frac{{\partial o\left( k \right)}}{{\partial {\theta _1}}} = \\ \xi \mathit{\boldsymbol{\cdot V}}_3^{\rm{T}}\mathit{\boldsymbol{\cdot}}{{\sigma '}_1}\left( {\mathit{\boldsymbol{V}}_1^{\rm{T}}\mathit{\boldsymbol{\cdot X}} + {\theta _1}} \right), \end{array} $ | (9) |
| $ \begin{array}{l} \;\;\;\;\frac{{\partial E\left( k \right)}}{{\partial {\mathit{\boldsymbol{V}}_2}}} = \frac{{\partial E\left( k \right)}}{{\partial o\left( k \right)}}\mathit{\boldsymbol{\cdot}}\frac{{\partial o\left( k \right)}}{{\partial {\mathit{\boldsymbol{V}}_2}}}{\rm{ = }}\\ \xi \mathit{\boldsymbol{\cdot V}}_4^{\rm{T}}\mathit{\boldsymbol{\cdot}}{{\sigma '}_2}\left( {\mathit{\boldsymbol{V}}_2^{\rm{T}}\mathit{\boldsymbol{\cdot O}} + {\theta _2}} \right)\mathit{\boldsymbol{\cdot O}}, \end{array} $ | (10) |
| $ \begin{array}{l} \;\;\;\;\;\;\frac{{\partial E\left( k \right)}}{{\partial {\theta _2}}} = \frac{{\partial E\left( k \right)}}{{\partial o\left( k \right)}}\mathit{\boldsymbol{\cdot}}\frac{{\partial o\left( k \right)}}{{\partial {\theta _2}}}{\rm{ = }}\\ \xi \mathit{\boldsymbol{\cdot V}}_4^{\rm{T}}\mathit{\boldsymbol{\cdot}}{{\sigma '}_2}\left( {\mathit{\boldsymbol{V}}_2^{\rm{T}}\mathit{\boldsymbol{\cdot O}} + {\theta _2}} \right). \end{array} $ | (11) |
为了提高收敛速度和鲁棒性,本研究采用基于Levenberg-Marquarqt算法[20, 21]的批量训练算法,即
| $ \begin{array}{l} \;\;\;\;\;\;\;{\mathit{\boldsymbol{M}}^{(l + 1)}} = {\mathit{\boldsymbol{M}}^{(l)}} - \\ {\left[ {{\mathit{\boldsymbol{J}}^{{\rm{T}}(l)}}\mathit{\boldsymbol{\cdot}}{\mathit{\boldsymbol{J}}^{(l)}} + \mu \mathit{\boldsymbol{\cdot I}}} \right]^{ - 1}}\mathit{\boldsymbol{\cdot}}{\mathit{\boldsymbol{J}}^{{\rm{T}}(l)}}\mathit{\boldsymbol{\cdot}}{e^{(l)}}, \end{array} $ | (12) |
式中,M为参数向量,即
| $ \mu = \left\{ {\begin{array}{*{20}{l}} {0.5 \times \mu , \;\;\;\;{e^{(l + 1)}} \le {e^{(l)}}}\\ {2.0 \times \mu , \;\;\;\;{e^{(l + 1)}} > {e^{(l)}}} \end{array}} \right.。$ | (13) |
为了验证所提出方案的有效性,在某高校随机抽取25名在校大学生进行EEG测试实验。根据该高校大学生心理健康综合测量过程中焦虑量表得分(SAS)情况可知,在所抽取的大学生中,需要心理干预和诊疗的人数(SAS>50)占比为24%,即不平衡度[19]IR=(1-24%)/24%=3.17,这与该高校的整体测量结果基本相符,存在“类别不平衡”问题。实验过程中,EEG数据采用Neuroscan公司的64导脑电设备及配套软件采集,设计不同颜色和不同朝向的Gapor patchs图片为刺激,采集通道为64个,采集频率为1 kHz,采集时间为10 min,即每位大学生的EEG数据长度为3.84×107个,具体的实验过程参见文献[26]的实验7。
值得注意的是,文献[26]是本课题组成员利用所采集的EEG数据来研究大学生在日常学习知识过程中的内隐觉察这一类心理认知问题,而视觉盲区实验是通过视觉来学习和接受新知识,不仅伴随着丰富的大脑活动信号,还包含着学习者的各种情绪变化状况[4]。此外,与章文佩等[1]采用考试过程的EEG信息来研究焦虑诊断问题相比,本研究采用视觉学习的EEG信号来诊断大学生的焦虑情绪,其准确性更高,主要原因是大学生们在考试过程中普遍会存在习得的紧张和焦虑情绪,而日常学习则更接近学生的实际情绪状态[3]。
2.2 CNN-QAL建模与泛化按照图 1的技术路线进行EEG焦虑情绪识别的建模与泛化检验。为了确保所提出的CNN-QAL模型具有足够的学习能力和建模精度,卷积-池化层的数量选择为3层,且卷积核的个数分别为16,32,64;设置卷积层和池化层的步长为1和2,而作用范围为5和2。对于新构建的末端NN-EIIS模型,其模型结构设置为m=4 096,n=3,H11=512,H12=8,H2=64。实际中,步长因子μ的初值设置为0.000 1,CNN-QAL模型经过100次迭代后的训练及泛化结果如图 4所示。为了更好地描述实验结果,对被试对象的序号按照其原始SAS从高到低重新排序,模型泛化的EEG数据同样来源于本课题组所采集的数据,即文献[26]的实验6,除了更换被试大学生和刺激所用的Gapor patchs图片以外,参数设置与建模实验都是相同的(图 4)。
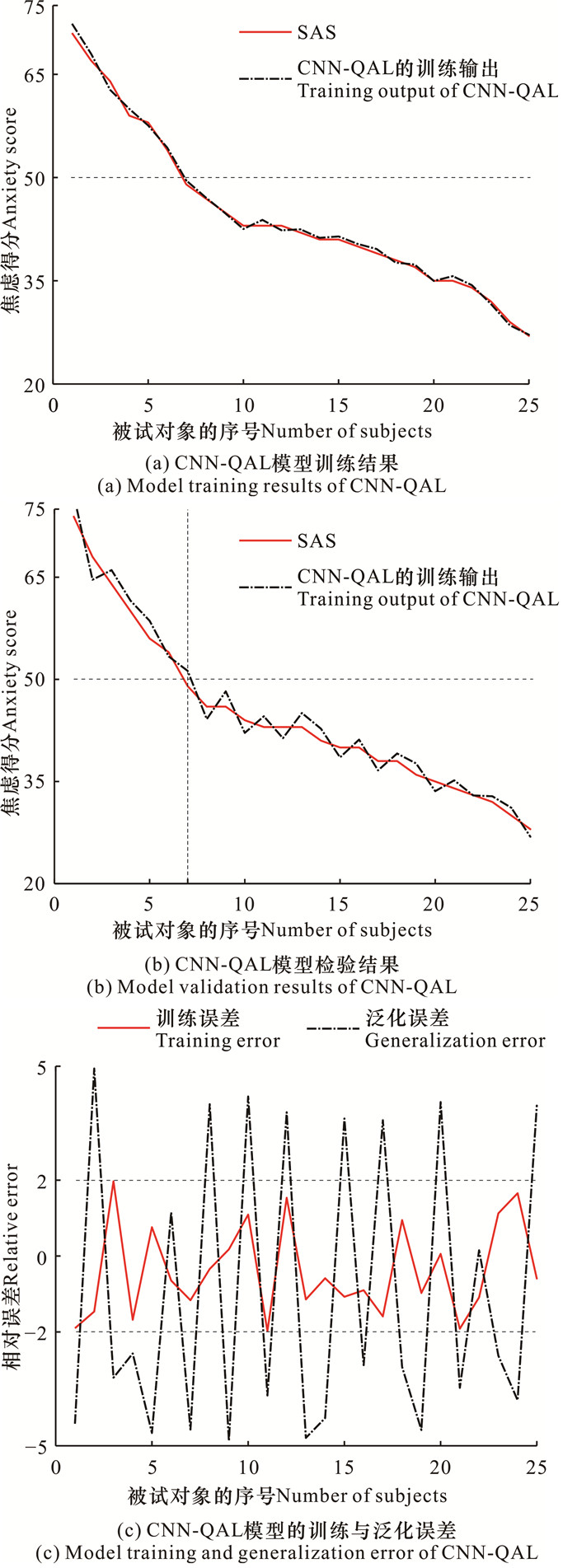
|
| 图 4 模型训练及泛化结果 Fig. 4 Model training and generalization results |
从图 4可知,训练所得到的CNN-QAL模型可以精确地逼近焦虑得分,其中,训练过程的相对误差在±2%以内,而泛化检验的相对误差在±5%以内。可见,即使被试样本集的不平衡度IR达到了3.17,CNN-QAL模型仍然能够精确地建模。由图 4(b)可知,CNN-QAL模型的泛化准确率为96%,只有第7个样本的泛化检验结果发生了偏差,该学生的SAS为49分,一般认为其不存在焦虑情绪;但CNN-QAL模型的泛化输出为51.24分,误将其识别为焦虑状态(>50分)。
2.3 实验结果对比分析与优化为进一步验证CNN-QAL模型的有效性,分别进行了两个方面的对比实验:与同类方法的横向对比实验、确定自身模型结构的内部分析优化实验。
① 横向对比实验。由于传统EEG分类方法的准确率较低,如Power Spectral Density+Support Vector Machine(PSD+SVM)约为73.4%[15],本研究仅与现有的深度学习方法比较,结果如表 1所示。
从表 1可知,CNN-QAL模型的准确率最高,主要原因是末端引入了具有连续逼近功能的NN-EIIS模型,识别精度比离散化的有限分类方法更具优势。但是,所有的识别算法在SAS临界状态更容易发生偏差,尤其是最接近50分的第7号被试大学生,误诊率最高。可见,对于SAS为临界状态的大学生,实际临床诊断还需要借助其他手段如访谈法[3]等进行识别,或将其列入“轻度焦虑”的范畴,通过增加心理咨询次数或服用抗焦虑的药物进行后续治疗。进一步分析可知,对于不具有连续量化识别的传统EEG焦虑情绪识别方法来说,本身没有焦虑情绪(如第8,9号)而被误诊的概率更大,这主要是由“类别不平衡”问题引起的,离散化的有限分类过程往往会向高概率一侧收敛[19],更易于产生误判,而采用本研究的量化识别方案可以有效解决这类问题。
② 内部分析优化实验。为了优化CNN-QAL模型结构,权衡网络结构、逼近精度、训练收敛速度之间的关系是一个重要的课题。实际研究过程中,对于CNN的前端特征提取部分,选择不同的网络结构进行对比分析,相关的网络训练收敛过程如图 5所示。

|
| 图 5 不同网络结构的训练收敛过程 Fig. 5 Training convergence process of different network structures |
从图 5可知,采用2层“卷积-池化”(卷积核个数分别为64,128,即曲线1)的训练精度较差且收敛速度很慢,MSE收敛曲线在训练过程中有较大波动(第60-65次)。另外3条曲线都采用了3层“卷积-池化”结构,只是卷积核个数有区别,其中,曲线2的收敛速度较慢,在第90次附近才基本进入稳态;曲线3和曲线4的收敛速度相差不大, 在第20次附近完成第一阶段的快速收敛,在第70次附近完成第二阶段收敛而进入稳态,但曲线4的卷积核数量比曲线3多一倍。可见,曲线3所对应网络结构的效果最佳。
3 讨论在实际心理临床治疗过程中,除了需要精确诊断出大学生是否存在焦虑情绪及其严重程度之外,还需要找准和判别每个大学生具体的病理因素,才能真正做到对症治疗。借助于心理医生的经验积累等,传统的访谈类诊断方式一般更具优势[3],这是目前各种EEG情绪诊断方法难以进行推广应用的主要阻碍。
本研究借鉴已有研究成果[20, 21],将病理因素当作建模过程中的一类中间状态,通过引入NN-EIIS模型,不仅解决EEG信号大学生焦虑情绪的精确量化识别问题,还能在一定程度上进行病理追溯分析。实际上,如果NN-EIIS模型的拓展输入空间[I,Ψ,O]具有完备性,不仅系统输出能被精确建模,而且中间状态(病理因素)也可以被精确逼近[20];在辨识所得的NN-EIIS模型中,如果把输入空间的特征信息与模型输出之间的权值传递链进行排序,找出主要的EEG特征信息并在时频域内进行盲源分离[27],就能够追溯这些EEG信号在大脑中的来源位置并获得对应的时频特征,实现对相关病理因素的追溯分析。以焦虑情绪最严重的第1号大学生患者为例,导致焦虑的EEG信号分布情况和对应的时频特征如图 6所示。
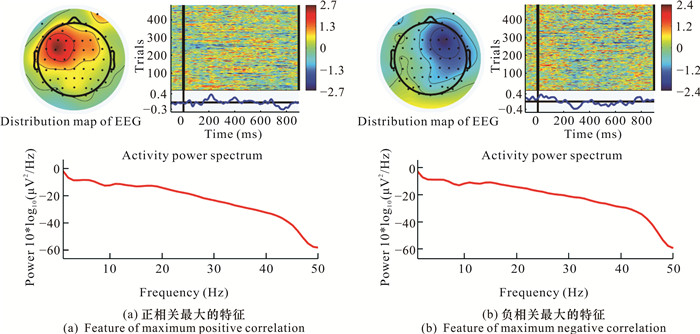
|
| 图 6 影响最大的内在因素的时频特征 Fig. 6 Time-frequency characteristics of the most influential internal factors |
结合脑电极布置[26]和图 6可知,导致焦虑情绪产生的EEG信号,主要来源于以F5-FC5和F6-FC6为中心的大脑区域内,属于人脑的左、右海马体部分。海马体负责记忆和学习,正常人会在有限次重复后,将一个短期记忆片段(如本实验的9个Gapor patchs子图片)转化为长期记忆,即海马体会将其转存入大脑皮层[28];如果在短期内再次出现这个记忆片段,对应的EEG信号将出现在大脑皮层而不是海马体。但是,从图 6的时频图可以看出,第1号焦虑情绪障碍患者的海马体均匀分布着强烈的EEG信号,这说明障碍者存在学习记忆障碍,无法将短期记忆片段正常地转化为长期记忆。
现有脑科学研究表明,海马体的长时间持续兴奋是导致紧张焦虑情绪的主要生理学原因,严重时将导致大脑出现一定程度的疼痛现象,这也与该大学生在实验过程中的表现和实验后的描述吻合。可见,应用本研究所提出的方案可将该大学生患者的病理因素初步追溯诊断为学习记忆障碍,至少是对具有快速变化且复杂的图像类知识点(如2.1节所述的Gapor patchs图片)进行学习的过程中,存在一定的记忆障碍。这类目前难以进行医学检测但却具有事实依据的、客观的病理追溯性诊断结论,对后期相关的心理治疗和心理危机干预是很有价值的。
4 结论针对现有EEG焦虑情感识别中存在的问题,本研究设计了一个CNN-QAL模型。通过在CNN模型末端引入并构造一个NN-EIIS模型来取代传统的分类器,并以被试对象的焦虑量表得分(SAS)作为整个系统的输出信号,使得CNN-QAL模型具备高精度定量逼近学习能力,有效解决了识别过程中“类别不平衡”的问题。并在此基础上结合现有的脑科学研究成果运用所获得的CNN-QAL模型,对具体大学生患者的特定病理因素进行了初步的追溯分析和探索,这对后续研究和实际的心理危机干预以及心理临床治疗具有有效的理论和实际价值,这将是下一步的研究方向。
| [1] |
章文佩, 沈群伦, 宋锦涛, 等. 基于事件相关电位(ERPs)和机器学习的考试焦虑诊断[J]. 心理学报, 2019, 51(10): 1116-1127. |
| [2] |
李伟. 文拉法辛对广泛性焦虑障碍患者大脑可塑性影响的研究[D]. 上海: 上海交通大学, 2018.
|
| [3] |
MCGLASHAN T H, WALSH B C, WOODS S W. The psychosis-risk syndrome: Handbook for diagnosis and follow-up[M]. New York: Oxford University Press, 2010.
|
| [4] |
庄宁. 基于脑电的情绪加工与识别技术研究[D]. 郑州: 中国人民解放军战略支援部队信息工程大学, 2020.
|
| [5] |
孙中皋, 薛全德, 王新军, 等. 基于脑电信号的情感识别方法综述[J]. 北京生物医学工程, 2020, 39(2): 186-195. DOI:10.3969/j.issn.1002-3208.2020.02.012 |
| [6] |
张冠华, 余旻婧, 陈果, 等. 面向情绪识别的脑电特征研究综述[J]. 中国科学(信息科学), 2019, 49(9): 1097-1118. |
| [7] |
胡理, 张治国. 脑电信号处理与特征提取[M]. 北京: 科学出版社, 2020.
|
| [8] |
CAND R A H, YUWONO M, CHAI R, et al. EEG emotion recognition using reduced channel wavelet entropy and average wavelet coefficient features with normal mutual information method[C]//Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). Jeju, Korea (South): IEEE, 2017: 463-466.
|
| [9] |
ZHENG W L, LU B L. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks[J]. IEEE Transactions on Autonomous Mental Development, 2015, 7(3): 162-175. DOI:10.1109/TAMD.2015.2431497 |
| [10] |
ALHAGRY S, FAHMY A A, EL-KHORIBI R A. Emotion recognition based on EEG using LSTM recurrent neural network[J]. International Journal of Advanced Computer Science and Applications, 2017, 8(10): 355-358. |
| [11] |
LIU Y, DING Y F, LI C. Multi-channel EEG-based emotion recognition via a multi-level features guided capsule network[J]. Computers in Biology and Medicine, 2020, 123(8): 103927. DOI:10.1016/j.compbiomed.2020.103927 |
| [12] |
覃晓, 黄呈铖, 施宇, 等. 基于卷积神经网络的图像分类研究进展[J]. 广西科学, 2020, 27(6): 587-599. |
| [13] |
邱锡鹏. 神经网络与深度学习[M]. 北京: 机械工业出版社, 2020.
|
| [14] |
GOODFELLOW I, BENGIO Y, COURVILLE A. Deep learning[M]. Cambridge, MA: MIT Press, 2016.
|
| [15] |
GAO Z K, LI Y L, YANG Y X, et al. A GPSO-optimized convolutional neural networks for EEG-based emotion recognition[J]. Neurocomputing, 2020, 380: 225-235. DOI:10.1016/j.neucom.2019.10.096 |
| [16] |
LI J P, ZHANG Z X, HE H G. Hierarchical convolutional neural networks for EEG-based emotion recognition[J]. Cognitive Computation, 2018, 10(2): 368-380. DOI:10.1007/s12559-017-9533-x |
| [17] |
ISSA S, PENG Q M, YOU X G. Emotion classification using EEG brain signals and the broad learning system[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(12): 7382-7391. DOI:10.1109/TSMC.2020.2969686 |
| [18] |
林泳昌, 朱晓姝. 一种基于SMOTE的不均衡样本KNN分类方法[J]. 广西科学, 2020, 27(3): 276-283. |
| [19] |
ROUT N, MISHRA D, MALLICK M K. Handling imbalanced data: A survey[C]//International Proceedings on Advances in Soft Computing, Intelligent Systems and Applications, Advances in Intelligent Systems and Computing(AISC), Singapore: Springer, 2017, 628: 431-443.
|
| [20] |
谢扬球. 基于三明治模型的非光滑非线性动态系统辨识与控制[D]. 西安: 西安电子科技大学, 2013.
|
| [21] |
XIE Y Q, TAN Y H, DONG R L. Nonlinear modeling and decoupling control of XY micro-positioning stages with piezoelectric actuators[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(3): 821-832. DOI:10.1109/TMECH.2012.2187794 |
| [22] |
张发启. 盲信号处理及应用[M]. 西安: 西安电子科技大学出版社, 2006.
|
| [23] |
陈峰练, 白琳, 张扬虎, 等. 基于混合深度学习的蔗糖原料蔗顶芽杂质探测技术[J]. 广西科学, 2021, 28(3): 242-248. |
| [24] |
张扬虎, 白琳, 陈峰练, 等. 基于深度卷积神经网络技术的棉花顶芽探测技术[J]. 广西科学, 2021, 28(3): 257-264. |
| [25] |
谢扬球, 谭永红. 压电陶瓷执行器的非光滑三明治模型辨识与内模控制[J]. 控制理论与应用, 2013, 30(5): 567-576. |
| [26] |
向往. 变化盲视下大学生内隐觉察的影响因素及脑电特征[D]. 天津: 天津师范大学, 2021.
|
| [27] |
高勇. 时频分析与盲信号处理[M]. 北京: 国防工业出版社, 2017.
|
| [28] |
田银, 徐鹏. 脑电与认知神经科学[M]. 北京: 科学出版社, 2021.
|



