近年来,癌症及恶性肿瘤一直威胁着人类的生命健康,尤其是患病早期症状不容易被查出,导致错过了最佳的治疗时间,因此,为各种疾病提供一种高效、准确的诊断方法,不仅可以让患者及时接受治疗,或许还可以挽救患者生命。随着基因微阵列技术的成熟,基因表达谱可以表示人类各个组织的正常基因,当前很多重大疾病的基因微阵列数据也已被共享,可为基因分类与识别提供大量可靠的数据。一般来说,在高维微阵列数据中,冗余的基因不仅会降低训练强度,而且会对学习算法的性能产生负面的影响。为了解决这些问题,研究人员提出了众多基因选择方法来选择最佳的鉴别基因[1]。
在进行基因微阵列分类时,最重要的是对微阵列基因进行特征选择,当前的基因选择方法主要分为过滤法、包装法、混合法和嵌入法等4类[2]。通常来说,包装法能提供更好的精度,在众多的包装法中,引力搜索算法(Gravity Search Algorithm,GSA)和教与学优化(Teaching-Learning-Based Optimization,TLBO)算法在生物信息学领域是众多研究的焦点[3-6]。由于这些技术在选择的基因之间缺乏相关性,从而会增加计算负担[7],为克服这些缺点,研究人员对许多混合进化算法进行了研究,如差分进化算法和人工蜂群算法的混合[8]、混合乌鸦搜索算法[9]、TLBO算法与GSA的结合[10]、特征选择集成算法和自适应蚱蜢优化算法的结合[11],以及二元精英花授粉算法和二分粒子群算法的融合[12]。但是大多数的混合智能算法仍存在很多缺陷,如执行时间高和陷入局部最优等。
本研究将GSA与二元TLBOGSA结合,利用GSA进行局部搜索,通过与二元TLBO融合来克服陷入局部最优的问题。同时,基于新型的粒子编码方法和适应度函数,提出基于BTLBOGSA的基因微阵列数据特征选择算法,该算法具有能提高数据集可解释性、降低计算复杂度、控制过早收敛和迭代停滞问题等潜在优点,可以提高收敛速度,平衡勘探开发能力之间的关系。通过将卷积神经网络(Convolutional Neural Network, CNN)用于微阵列数据分类器,提出基于BTLBOGSA与CNN的基因微阵列数据分类模型,该模型可从不同的微阵列数据集中选择具有高度鉴别性的基因子集,相对于使用全部基因进行分类时更不容易过拟合,具有较高的分类精度。
1 相关理论基础 1.1 教与学优化算法教与学优化(TLBO)算法是近些年比较流行的进化算法(EAs)之一[13]。TLBO算法模拟课堂教学和学习过程可分为教师教学和学生学习两个阶段。
教师教学阶段是指教师通过教学以提高学生的知识水平。教学过程计算式如下:
| $ {X_{i, k + 1}} = {X_{i, k}} + {r_i} \times ({X_{{\rm{teacher}}, k}} - {T_f} \times {M_{i, k}}), $ | (1) |
式中,Xi, k和Xi, k+1分别表示第i个学员在第k次和第k+1次迭代时学习的值;Xteacher, k为算法在第k次迭代时的最佳学习者;ri为[0, 1]之间的随机值;T为班级教室;Tf为教师因子,Mi, k为当前班级平均成绩。Tf的更新公式如下:
| $ {T_f} = {\rm{round}}[1 + {\rm{rand}}(0, 1)]。$ | (2) |
学生学习阶段是指学生相互交流、学习知识以及丰富知识。学习阶段计算式如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;{X_{i, k + 1}} = \\ \left\{ {\begin{array}{*{20}{c}} {{X_{i, k}} + {r_i} \times \left( {{X_p} - {X_q}} \right), f\left( {{X_q}} \right) > f\left( {{X_p}} \right)}\\ {{X_{i, k}} + {r_i} \times \left( {{X_q} - {X_p}} \right), 其他} \end{array}} \right.{\rm{ }}, \end{array} $ | (3) |
式中,Xi, k和Xi, k+1分别表示第i个学员在第k次和第k+1次迭代时学习前和学习后的值;Xp和Xq分别为第i个学生及同一个班级内的另外一个学生,且i≠j;ri为[0, 1]之间的随机值;f(g)为要优化的目标函数。
1.2 引力搜索算法引力搜索算法(GSA)是伊朗学者Esmat于2009年提出的一种新型群智能优化算法[14]。GSA中第i个粒子的质量Mi(t)的计算式为
| $ {M_i}\left( t \right) = \frac{{{m_i}\left( t \right)}}{{\sum\limits_{j = 1}^N {{m_j}\left( t \right)} }}, $ | (4) |
| $ {m_i}\left( t \right) = \frac{{fi{t_i}\left( t \right) - worst\left( t \right)}}{{best\left( t \right) - worst\left( t \right)}}, $ | (5) |
式中,mi(t)和mj(t)分别为第i和j个粒子相对于迭代中最好和最差适应度的占比,用于粒子质量的计算;N为粒子总数;fiti(t)为第i个粒子在第t次迭代的适应度;best(t)、worst(t)分别为迭代时所有粒子中最好和最差的适应度,且根据优化目标的不同分为求解最大值和最小值问题,具体如下:
| $ \left\{ {\begin{array}{*{20}{l}} {best\left( t \right) = {\rm{max}}\left\{ {fi{t_i}\left( t \right)} \right\}}\\ {worst\left( t \right) = {\rm{min}}\left\{ {fi{t_i}\left( t \right)} \right\}} \end{array}} \right., i = 1, 2, \cdots , N, $ | (6) |
| $ \left\{ {\begin{array}{*{20}{l}} {best\left( t \right) = {\rm{min}}\left\{ {fi{t_i}\left( t \right)} \right\}}\\ {worst\left( t \right) = {\rm{max}}\left\{ {fi{t_i}\left( t \right)} \right\}} \end{array}} \right., i = 1, 2, \cdots , N, $ | (7) |
粒子间引力
| $ \begin{array}{l} \;\;\;\;\;\;\;\;F_{ij}^d = \left( t \right) = G\left( t \right)\frac{{{M_i}\left( t \right) \times {M_j}\left( t \right)}}{{{R_{ij}}\left( t \right) + \varepsilon }}\left( {X_j^d\left( t \right) - } \right.\\ \left. {X_i^d\left( t \right)} \right), \end{array} $ | (8) |
式中,Rij(t)为两粒子间的欧氏距离;ε为很小的常量,保证分母不为0;
| $ G\left( t \right) = {G_0}{e^{{\rm{ - }}\frac{{\alpha t}}{T}}}, $ | (9) |
式中,G0为初始引力;T为最大迭代次数;α为衰减系数。
粒子受该合力作用下产生的加速度
| $ \alpha _i^d(t) = \frac{{F_i^d\left( t \right)}}{{{M_i}\left( t \right)}}。$ | (10) |
特征选择的主要目标是从原始特征空间中选择具有最小冗余和最大鉴别能力的相关特征。通过减少不相关和无意义的特征,缩减数据维数,可以降低分类算法所需的数据量及执行时间,从而提高分类器的性能。元启发式技术因其全局搜索能力而闻名,在寻找给定问题的最优基因子集时,已有多种元启发式算法,如遗传算法、引力搜索算法、教与学优化算法、差分变异算法和粒子群优化算法,用于优化特征选择问题[15, 16]。TLBO算法和GSA是计算智能领域中两种著名的元启发式方法。在当前的研究中,尚未有关于TLBO算法和GSA在基因微阵列高维数据集上的组合应用。本文将TLBO算法和GSA结合起来进行基因微阵列高维数据的特征提取。
2.1 二元TLBOGSATLBOGSA已被用于解决复杂的连续型全局优化问题,由于个体在连续型搜索空间中移动,所以位置向量为连续型变量[17]。在特征选择问题上,个体需在二元搜索空间中移动,因此提出了TLBOGSA的二元变体,称为BTLBOGSA。在BTLBOGSA中,教师教学和学生学习两个阶段的粒子速度更新公式分别为
| $ \begin{array}{l} \;\;\;\;\;\;\;V_i^{k + 1} = {r_1}*\left( {{X_{{\rm{teacher}}, k}} - {T_f}*{M_{i, k}}} \right) + \\ {r_2}*(\alpha _i^k\left( t \right) - {T_f}*{M_{i, k}}), \end{array} $ | (11) |
| $ V_i^{k + 1} = {r_3}*({X_p} - {X_q}), $ | (12) |
式中,
在BTLBOGSA中,相关的位置向量用二进制表示,但速度向量仍是浮点型。速度向量的用途主要是为了寻找学习者在一个位置上变化的概率,即从0变为1或者1变为0的概率。通常情况下,为将连续搜索空间映射到离散搜索空间,需要使用特有的转换函数,最常用的函数是sigmoid函数。使用sigmoid函数的缺点是正向速度和负向速度间的差异不明显,导致原先的位置向量需要更大的运动速度才能更新。为了克服这个问题,提出了一种新的速度向量转换函数,具体如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;T\left( {V_i^k} \right) = {\rm{exp}}\left( {|\left( {V_i^{k + 1} - \alpha } \right)|} \right) - 1/{\rm{exp}}\left( {|\left( {V_i^{k + 1} - } \right.} \right.\\ \left. \alpha \right)/\left( {1 + b} \right)\left. | \right) + 1, \end{array} $ | (13) |
式中,
| $ {X_{i, k}} = \left\{ {\begin{array}{*{20}{L}} {1\;\;\;\;{\rm{if rand}}() < T\left( {V_i^k} \right)}\\ {0\;\;\;\;\;\;\;\;{\rm{otherwise}}} \end{array}} \right.。$ | (14) |
在基因微阵列数据分类中,仅由适应度函数指定的最优特征子集可能具有潜在的冗余,为提高基因微阵列数据分类精度和最小化特征数量,研究了一种新的适应度函数,具体如下:
| $ fitness\left( x \right) = \alpha *\frac{\beta }{\vartheta } + \left( {1 - \alpha } \right)*\gamma , $ | (15) |
式中,fitness(x)为特征子集x的分类能力;γ为分类器的分类精度;ϑ为染色体的长度;β为候选特征子集中特征长度的上界;α为0到1之间的常数。
2.4 算法实现步骤基于TLBO算法和GSA进行基因微阵列高维数据的特征选择,在此基础上提出了基于BTLBOGSA的基因微阵列数据特征选择方法,具体实现如下:
步骤1:初始化种群大小、维度D及初始的特征子集Z等;
步骤2:设置算法初始运行次数t=1,最大运行次数为Tmax;
步骤3:计算种群中每个学习者的适应度值,并记录最佳学习者;
步骤4:根据公式(9)计算当前迭代次数时的引力常量G(t);
步骤5:根据公式(6)(7)更新当前迭代次数时的最佳适应度值best(t)和最差适应度值worst(t);
步骤6:根据公式(4)更新当前迭代次数时每个学习者的Mi(t);
步骤7:根据公式(8)计算当前迭代次数时所有学习者的引力强度
步骤8:根据公式(10)计算当前迭代次数时所有学习者的加速系数
步骤9:根据公式(13)计算当前迭代次数时所有学习者位置向量改变的可能性;
步骤10:根据公式(14)计算当前迭代次数时所有学习者的位置向量Xi, k;
步骤11:根据公式(11)、(12)计算当前迭代次数时所有学习者的速度向量;
步骤12:根据公式(15)计算当前迭代次数时所有学习者的适应度值;
步骤13:更新所有学习者的位置向量及特征子集结果Z;
步骤14:保存具有最高适应度值的特征子集;
步骤15:跳转到步骤3,直到达到设置的运行次数,结束算法运行。
3 基于BTLBOGSA与CNN的基因微阵列数据分类模型基于BTLBOGSA模型可实现基因微阵列数据的特征维度缩减,在此基础上提出了基于BTLBOGSA与CNN[18]的基因微阵列数据分类模型。BTLBOGSA-CNN模型的实现步骤如图 1所示。

|
| 图 1 BTLBOGSA-CNN模型流程图 Fig. 1 Flow chart of BTLBOGSA-CNN model |
步骤1:数据预处理;
步骤2:将数据集按照7∶3的比例划分为训练集和测试集;
步骤3:利用BTLBOGSA进行训练集数据的特征选择,实现数据特征维度缩减;
步骤4:利用CNN模型进行训练集数据分类;
步骤5:利用训练好的模型进行测试集数据分类;
步骤6:保存分类结果。
4 实验与仿真结果 4.1 实验环境及评价指标在实验中采用的开发语言为Python3.8.2,操作系统为Ubuntu 18.04.5(64位),CPU为8核2.90 GHz,GPU为GTX 1080Ti,内存为16 GB,硬盘为500 GB。为了评估BTLBOGSA-CNN模型的性能,采用基因微阵列数据分类中常用的敏感性Sensitivity(Se)、特异性Specificity(Sp)、马修斯相关系数MCC和F-score(Fmes)值4个指标作为评估指标。这些指标的计算方法如下:
| $ {\rm{Sensitivity}}\left( {{\rm{Se}}} \right){\rm{ = }}\frac{{{\rm{TP }}}}{{{\rm{TP + FN}}}}, $ | (16) |
| $ {\rm{Specificity}}\left( {{\rm{Sp}}} \right){\rm{ = }}\frac{{{\rm{TN}}}}{{{\rm{TN + FP}}}}, $ | (17) |
| $ {\rm{F - score}}\left( {{\rm{Fmes}}} \right){\rm{ = }}\frac{{{\rm{2 \times TP}}}}{{{\rm{2*TP + FN + FP}}}}, $ | (18) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;{\rm{MCC = }}\\ \frac{{{\rm{TN*TP - FN*FP}}}}{{\sqrt {\left( {{\rm{TP + FP}}} \right){\rm{ + }}\left( {{\rm{TP + FN}}} \right){\rm{ + }}\left( {{\rm{TN + FP}}} \right){\rm{ + }}\left( {{\rm{TN + FN}}} \right)} }}, \end{array} $ | (19) |
式中,TP、TN、FP和FN在独立的数据集中分别为真阳性、真阴性、假阳性和假阴性。
4.2 实验数据集使用Leukaemia-1、Colon-cancer、DLBCL、Leukaemia-2和Prostate-tumour 5种基因表达数据集对提出的方法进行验证。表 1总结了关于数据集的一些基本信息,包括特征数量、基因数和类别等。
| 序号No. | 数据集Data set | 特征数量Number of features | 基因数Number of genes | 类别Classification |
| 1 | Leukaemia-1 | 72 | 5 327 | 3 |
| 2 | Colon-cancer | 62 | 2 000 | 2 |
| 3 | DLBCL | 77 | 5 496 | 2 |
| 4 | Leukaemia-2 | 72 | 11 225 | 3 |
| 5 | Prostate-tumour | 102 | 10 509 | 2 |
4.3 模型参数设置
本文使用网格搜索法对BTLBOGSA-CNN模型进行实验,取具有最好分类效果的模型参数作为与其他模型对比时的参数。具体参数设置如表 2所示。
| 序号No. | 参数Parameters | 值Value | 序号No. | 参数Parameters | 值Value |
| 1 | 种群规模Size of population | 20 | 9 | ω | 0.7 |
| 2 | 迭代次数Number of iterations | 100 | 10 | ρ | 0.7 |
| 3 | 运行次数Number of runs | 10 | 11 | Pc | 0.7 |
| 4 | 基因长度Length of genes | 50 | 12 | Pm | 0.4 |
| 5 | 性能指标Index of performance | Accuracy | 13 | c1、c2 | 2 |
| 6 | Epoch | 100 | 14 | 优化器Optimizer | SGD |
| 7 | 学习率Rate of learning | 0.001 | 15 | 激活函数Activation function | RELU |
| 8 | 批处理大小Size of batch | 64 | 16 | 输出函数Output function | Softmax |
4.4 实验对比分析
为充分验证BTLBOGSA-CNN模型的性能,首先将BTLBOGSA与TLBO算法、GSA结合分别对5个基因微阵列数据集进行数据特征选择,验证基于BTLBOGSA进行特征选择的有效性;然后将BTLBOGSA-CNN、CNN、TLBO-CNN和GSA-CNN进行基因微阵列数据集的分类,验证BTLBOGSA与CNN结合在一起的有效性;最后将BTLBOGSA-CNN与CMIM[19]、JMI[20]、mRMR[21]、ITAFSVM[22]、TLBOGSA-SVM等其他已有分类模型进行对比,验证BTLBOGSA-CNN模型相对于已有模型的有效性。
4.4.1 BTLBOGSA、TLBO算法和GSA的特征选择利用BTLBOGSA、TLBO算法和GSA对5个基因微阵列数据集进行数据特征选择,特征选择结果如图 2所示。在5个数据集上,基于BTLBOGSA进行基因微阵列数据特征选择的有效特征数均少于TLBO、GSA算法,有效降低了数据特征维度,表明基于BTLBOGSA的基因微阵列数据特征选择算法具有更好的降维效果。

|
| 图 2 3种算法的特征选择结果 Fig. 2 Feature selection results of three algorithms |
4.4.2 BTLBOGSA-CNN、CNN、TLBO-CNN和GSA-CNN的分类
分别利用BTLBOGSA-CNN、CNN、TLBO-CNN和GSA-CNN对5个基因微阵列数据集进行数据分类,结果如图 3所示。在数据集DLBCL上,BTLBOGSA-CNN模型相对于其余3个模型分类结果的Sensitivity(Se)值最高提升8.25%,在其余4种数据集上最低提升0.23%。对于任意数据集,BTLBOGSA-CNN模型均具有最好的表现。BTLBOGSA-CNN相对于CNN具有更好的分类效果,主要是因为在利用CNN分类前使用BTLBOGSA对数据特征进行提取,得到具有更优分类效果的特征集合;BTLBOGSA-CNN相对于TLBO-CNN、GSA-CNN具有更好的分类效果,则主要是因为BTLBOGSA将TLBO和GSA的优点结合起来,采用了新型的编码策略,使得其能够寻找到更有分类效果的特征集合,从而使得利用CNN对数据进行分类时具有更好的分类精度。

|
| 图 3 4种模型分类结果 Fig. 3 Classification results of four models |
4.4.3 BTLBOGSA-CNN与其他已有分类模型对比分析
利用BTLBOGSA-CNN与其他5种已有算法模型对5个基因微阵列数据集进行数据分类,结果如图 4所示。以数据集Leukaemia-1为例,BTLBOGSA-CNN模型相对于其余5种模型分类结果的Sensitivity(Se)值至少提高0.22%,Specificity(Sp)值至少提高0.52%,F-score(Fmes)值至少提高0.34%,MCC值至少提高0.11%。在5个数据集上,BTLBOGSA-CNN相对于其余模型均具有更好的分类效果,主要是因为BTLBOGSA-CNN模型相对于其他算法,一方面将TLBO与GSA算法结合起来,充分发挥了两者的优势,通过基因微阵列数据特征的有效提取, 实现微阵列数据维度的缩减;另一方面充分发挥卷积神经网络CNN的优势,利用其进行特征提取后,实现微阵列数据的高精度分类。
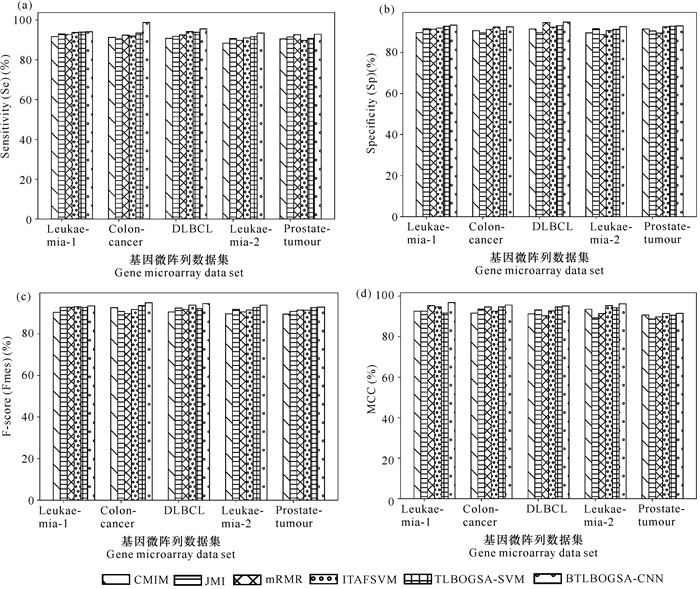
|
| 图 4 6种模型分类结果 Fig. 4 Classification results of six model |
5 结论
针对当前基因微阵列数据处理面临的数据维度高、分类精度低的问题,构建了基于BTLBOGSA与CNN的基因微阵列数据分类模型(BTLBOGSA-CNN)。该模型基于BTLBOGSA进行基因微阵列数据的特征选择,实现基因微阵列数据维度的缩减,并利用CNN实现基因微阵列数据的分类。在实验中,将BTLBOGSA-CNN与其他分类模型进行对比,结果表明BTLBOGSA-CNN相对于已有模型可以更好地进行基因表达谱数据分类,具有更高的分类精度。但是,由于TLBO算法与GSA的局限性,BTLBOGSA-CNN模型无法对特征规模过大的基因数据集进行有效分析。在后续的研究中,将着重分析基因特征之间的关联性,设计出更有效的特征选择算法,以便于实现对癌症及恶性肿瘤等疾病的有效预测。
| [1] |
余慧敏. 基于小样本高维基因数据的头颈癌局部复发预测[D]. 西安: 西安邮电大学, 2020.
|
| [2] |
JAHWAR A F, AHMED N S. Swarm intelligence algorithms in gene selection profile based on classification of microarray data: A review[J]. Journal of Applied Science and Technology Trends, 2021, 2(1): 1-9. DOI:10.38094/jastt20161 |
| [3] |
GAO W F, HU L, ZHANG P. Feature redundancy term variation for mutual information-based feature selection[J]. Applied Intelligence, 2020, 50(4): 1272-1288. DOI:10.1007/s10489-019-01597-z |
| [4] |
JUBAIR S, ALKHATEEB A, TABL A A, et al. A novel approach to identify subtype-specific network biomarkers of breast cancer survivability[J]. Network Modeling Analysis in Health Informatics and Bioinformatics, 2020, 9(1): 1-12. DOI:10.1007/s13721-019-0207-3 |
| [5] |
刁鹏飞, 李树森, 姜雪松. 基于多种群分解预测的动态多目标引力搜索算法[J]. 控制与决策, 2021, 36(12): 2910-2918. |
| [6] |
BUREERAT S, SLEESONGSOM S. Constraint han- dling technique for four-bar linkage path generation using self-adaptive teaching-learning-based optimization with a diversity archive[J]. Engineering Optimization, 2021, 53(3): 513-530. DOI:10.1080/0305215X.2020.1741566 |
| [7] |
SHUKLA A K, SINGH P, VARDHAN M. An adaptive inertia weight teaching-learning-based optimization algorithm and its applications[J]. Applied Mathematical Modelling, 2020, 77(7): 309-326. |
| [8] |
BABANEZHAD M, ZABIHI S, BEHROYAN I, et al. Prediction of gas velocity in two-phase flow using developed fuzzy logic system with differential evolution algorithm[J]. Scientific Reports, 2021, 11(1): 2380. DOI:10.1038/s41598-021-81957-3 |
| [9] |
GHOLAMI J, MARDUKHI F, ZAWBAA H M. An improved crow search algorithm for solving numerical optimization functions[J]. Soft Computing, 2021, 25: 9441-9454. DOI:10.1007/s00500-021-05827-w |
| [10] |
SINGH M, SINGH S. Multi-objective optimization of electrical discharge machining of nimonic 75 using teaching learning based optimization (TLBO) algorithm[J]. Materials Today: Proceedings, 2020, 24: 576-584. DOI:10.1016/j.matpr.2020.04.311 |
| [11] |
DWIVEDI S, VARDHAN M, TRIPATHI S, et al. Implementation of adaptive scheme in evolutionary technique for anomaly-based intrusion detection[J]. Evolutionary Intelligence, 2020, 13(1): 103-117. DOI:10.1007/s12065-019-00293-8 |
| [12] |
PASHAEI E, PASHAEI E. Gene selection using hybrid dragonfly black hole algorithm: A case study on RNA-seq COVID-19 data[J]. Analytical Biochemistry, 2021, 627: 114242. DOI:10.1016/j.ab.2021.114242 |
| [13] |
林伟豪, 何杰光, 刘婷婷, 等. 一种改进的多学习教与学优化算法[J]. 2018, 28(1): 33-38.
|
| [14] |
张娜, 赵泽丹, 包晓安, 等. 基于改进的Tent混沌万有引力搜索算法[J]. 控制与决策, 2020, 35(4): 893-900. |
| [15] |
FENG J, JIAO L C, LIU F, et al. Mutual-information-based semi-supervised hyperspectral band selection with high discrimination, high information, and low redundancy[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 53(5): 2956-2969. |
| [16] |
ÖZÇIFT A, GÜLTEN A. Genetic algorithm wrapped Bayesian network feature selection applied to differential diagnosis of erythemato-squamous diseases[J]. Digital Signal Processing, 2013, 23(1): 230-237. DOI:10.1016/j.dsp.2012.07.008 |
| [17] |
SHUKLA A K, TRIPATHI D, REDDY B R, et al. A study on metaheuristics approaches for gene selection in microarray data: Algorithms, pplications and open challenges[J]. Evolutionary Intelligence, 2020, 13(3): 309-329. DOI:10.1007/s12065-019-00306-6 |
| [18] |
KUMAR A, GANDHI C P, ZHOU Y Q, et al. Im- proved deep convolution neural network (CNN) for the identification of defects in the centrifugal pump using acoustic images[J]. Applied Acoustics, 2020, 167: 107399. DOI:10.1016/j.apacoust.2020.107399 |
| [19] |
WANG L X, JIANG S Y, JIANG S Y. A feature selection method via analysis of relevance, redundancy, and interaction[J]. Expert Systems with Applications, 2021, 183: 115365. DOI:10.1016/j.eswa.2021.115365 |
| [20] |
雍菊亚, 周忠眉. 基于互信息的多级特征选择算法[J]. 计算机应用, 2020, 40(12): 3478-3484. |
| [21] |
EL KAFRAWY P, FATHI H, QARAAD M, et al. An efficient SVM-Based feature selection model for cancer classification using high-dimensional microarray data[J]. IEEE Access, 2021, 9: 155353-155369. DOI:10.1109/ACCESS.2021.3123090 |
| [22] |
戴宏亮. 基于ITAFSVM的微阵列数据特征选择和分类[J]. 中山大学学报(自然科学版), 2010, 49(2): 37-42. |



