2. 南京信息工程大学,江苏南京 210044
2. Nanjing University of Information Science and Technology, Nanjing, Jiangsu, 210044, China
人体的呼吸信号涵盖多方面的信息特征,如速率、形态、强度等,这些信息可有效体现如心肺功能等人体多方面功能特征。呼吸数据相关文献表明,人体呼吸信号确实能在一定程度上反映人的身体状况,因此对人类呼吸病症的有效预防与及时发现,可以通过分析人体呼吸信号来实现[1]。
相较于基础的呼吸信号获取,国外的研究人员更多着眼于获取呼吸数据或者通过实时呼吸数据进行疾病预警[2, 3]。Sebastijan等[4]提出利用光学干涉仪对外部干扰造成光纤长度变化的特性来检测呼吸。Alexander等[5]选取33个呼吸关联特征结合睡眠阶段的启发式知识进行特征分类,用于判断呼吸数据来自健康人还是病人,准确率达到80.38%。Agnel等[6]基于单片机设计了一个监测系统,用于测量睡眠状态下受试者呼吸出现暂停的状况。Raji等[7]通过两个LM35温度传感器间接获取患者呼吸样本信息,然后根据呼吸率的特殊波动状况来判断患者是否哮喘发作。研究人员的共同目标是从简单的长时程呼吸信号中提取精准的呼吸信号,并将其应用于呼气功能检测或疾病诊断等。但目前的研究多数仅是通过实时监控呼吸数据来查看是否出现异常情况,并没有对患者的呼吸系统进行全面评估。
此外,对呼吸信号的分析和研究仍然存在许多有待突破的关键技术和难点:①如何对最初采集到的呼吸信号进行预处理。因为刚采集的、最初始的呼吸信号中存在大量噪声数据,如果直接用来进行后续研究,将影响最后的实验结果,因此需要先去除信号中的噪声,为后续研究的开展打下良好的基础。②不同阶段的呼吸信号数据与心电信号数据有明显不同,这可能是说话、打喷嚏、咳嗽等行为所导致的数据采集不准确,此外,还存在除了“吸气”“呼气”之外,无法更加细分呼吸信号程度的问题,这些问题都是开展进一步研究的巨大挑战。③因为呼吸信号本身的属性有一定程度的不确定因素,所以在对其做相关研究时,如何提高结果的精确度是个棘手的问题。相对于传统的X光、核磁、呼吸机检测仪器等测量手段,使用呼吸腰带测量呼吸具有持续采集、对人体几乎没有伤害、方便、价格低、信号采集相对稳定等优点,且呼吸腰带获取的呼吸数据是具有时间序列特征的连续数据。因此,本研究使用呼吸腰带获取受试者呼吸信号数据,先对原始呼吸信号进行滤波处理,去除相应的异常数值与基线漂移情况;然后分别使用适合处理时间序列的长短期记忆网络(Long Short-Term Memory, LSTM)、吸呼比结合LSTM,以及吸呼比结合在许多领域被广泛应用的支持向量机(Support Vector Machine, SVM),对收集到的呼吸数据进行分类,判断受试者的呼吸状况是否异常。
1 数据来源与方法 1.1 数据来源受试者呼吸信号数据均采用呼吸腰带获取。实验数据集由中国中医科学院采集,总样本数量为342个,其中包含人体呼吸异常55个、正常287个,在全部的样例中,单个样例均为24 h左右的十进制数值。正常人的吸气时间一般为0.8-1.2 s,呼气时间一般为0.5-1.0 s[1],加上1-2 s的呼吸间隔,一次呼吸的时间约3.5 s,吸气与呼气时间比为1∶(1.5-2.0)。由于呼气时仅是胸腔回缩而没有其他动能,所以需要的时间较长,但异常人群的呼吸比值会达到正常人的两倍甚至更高。因此,针对有明显差异的信息,可以收集对应的呼吸数据进行深层次的分析。
1.2 呼吸数据处理原始数据通常存在基线漂移等现象。基线漂移一般是由于人体呼吸、电极运动等引起的,在进行下一步的研究分析之前,需要先从原数据中去除基线漂移才能得到更体现原始呼吸特征的数据。常用的去除方法有中值滤波、小波变换法、形态学滤波法等[8]。本研究选用小波变换进行滤波处理。
小波变换广泛应用于信号处理、图像处理、模式识别等领域。通过伸缩平移运算对信号(函数)逐步进行多尺度细化,最终达到高频处时间细分、低频处频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节。小波变换是一个平方可积分函数与一个在时频域上均具有良好局部性质的小波函数的内积,如公式(1)所示。
| $ \begin{array}{l} {W_f}\left( {a, b} \right) = \left\langle {f, {\psi _{a, b}}} \right\rangle = \\ \frac{1}{{\sqrt a }}\int_{ - \infty }^{ + \infty } {f\left( t \right){\psi ^*}\left( {\frac{{t - b}}{a}} \right)} dt, \end{array} $ | (1) |
式中,a>0,为尺度因子;b为位移因子;*表示复数共轭;ψa, b(t)为小波基函数。
采用滤波的方式对最初的数据进行处理,呼吸频率一般为0.2-0.8 Hz,先用Butterworth低通滤波器消除高频噪声,其中将操作中的截止频率和采样频率分别定为0.8 Hz和32 Hz。公式(2)为呼吸曲线基准的计算方法,式子中样例点的数量用m表示,第i个数据点的大小用xi表示。
| $ bl = \frac{1}{m}\sum\limits_{i = 1}^m {{x_i}} 。$ | (2) |
单个样例出现个体性差异的现象属于正常范畴。本研究利用公式(3)的处理方法对没有关系的差异性进行有效消除和分类。
| $ {d^\prime }_n = {d_n} - bl, $ | (3) |
式中,点n的信号大小用dn表示,点n经过相关处理操作后的信号大小用d′n表示,呼吸信号均值用bl表示,同时把所有单例的基准全部设定为0。下一步针对所有的波形执行针对基线漂移的消除操作,首先要找出其中的拐点信息。对每两个拐点间的数据使用公式(4)计算获取其新点的位置。
| $ x\prime = \sum\limits_{i = 1}^L {[{x_i} - (\frac{{{d_a} + {d_b}}}{2} - bl)]} , $ | (4) |
式中,da为图 1中a点的数值,db为图 1中b点处的数值,L表示图 1中所有数值位于da和db间的关键点的个数。呼吸时会存在一些相对较小的波折(如图 1中红色标记处),这些波折不可以当作真正的拐点,因此,设定一个经验阈值的大小为σ=0.5,针对波峰波谷的垂直方向的距离大小进行相关的测量,如果测量值小于设定阈值的大小,那么该点将不会被当作拐点。

|
| 图 1 拐点(波峰/波谷)示意图 Fig. 1 Schematic diagram of inflection point (peak/trough) |
1.3 吸呼比特征
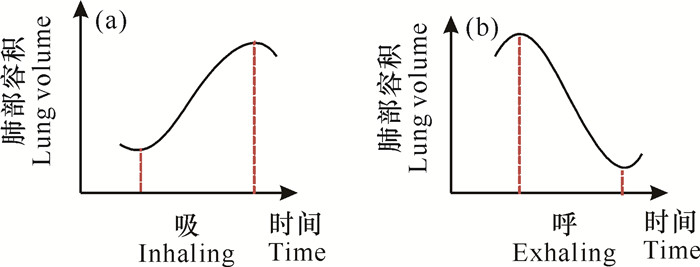
呼吸数据的相关分析常用的指标是吸呼比特征,吸呼比即一次呼吸周期中的吸气时间与呼气时间的比值。根据其特点可识别出数据中的峰值和谷值,呈上升趋势的为“吸”,下降趋势则为“呼”。图 2(a)为“吸”在呼吸带上的压力变化过程,体现了“吸”过程中肺部容积逐渐增大;图 2(b)为“呼”在呼吸带上的压力变化过程,体现了“呼”过程中肺部容积逐渐减小。各自的时间代表“呼”和“吸”维持的时长。
|
| 图 2 “吸”“呼”过程示意图 Fig. 2 Schematic diagram of "inhaling" and "exhaling" process |
得到“吸”与“呼”的时间后,则吸呼比特征可根据公式(5)计算得到,其中tx和th分别代表一次吸和呼的时间长度。
| $ \alpha = {t_x}/{t_h}。$ | (5) |
LSTM是一种特殊的循环神经网络(Recurrent Neural Network, RNN)。对于RNN,LSTM能够更好地处理RNN面临的梯度爆炸和梯度消失问题,这主要是因为LSTM摒弃了简单RNN中“连乘”的计算方式,改为“累加”的方式[9]。LSTM引入了记忆单元,这样网络可以控制什么时候遗忘不需要的信息,什么时候用新的输入信息更新记忆单元,通过遗忘门、输入门、输出门来实现信息的保护和控制。在t时刻LSTM更新方式如下:
| $ \begin{array}{l} {f_t} = \sigma ({W_f}\cdot\left[ {{h_{t - 1}}, {x_t}} \right] + {b_f}), \\ {i_t} = \sigma ({W_i}\cdot\left[ {{h_{t - 1}}, {x_t}} \right] + {b_i}), \\ {{\tilde C}_t} = {\rm{tanh}}({W_C}\cdot\left[ {{h_{t - 1}}, {x_t}} \right] + {b_c}), \\ {C_t} = {f_t}*{C_{t - 1}} + {i_t}*{{\tilde C}_t}, \\ {o_t} = \sigma ({W_o}\cdot\left[ {{h_{t - 1}}, {x_t}} \right] + {b_o}), \\ {h_t} = {o_t}{\rm{*tanh}}\left( {{C_t}} \right), \end{array} $ | (6) |
式中,ht-1为上一时刻的输出,xt为t时刻的输入,σ是激活函数。遗忘门ft控制每一个单元需要遗忘多少信息,输入门it控制新的信息,输出门ot控制输出的信息。
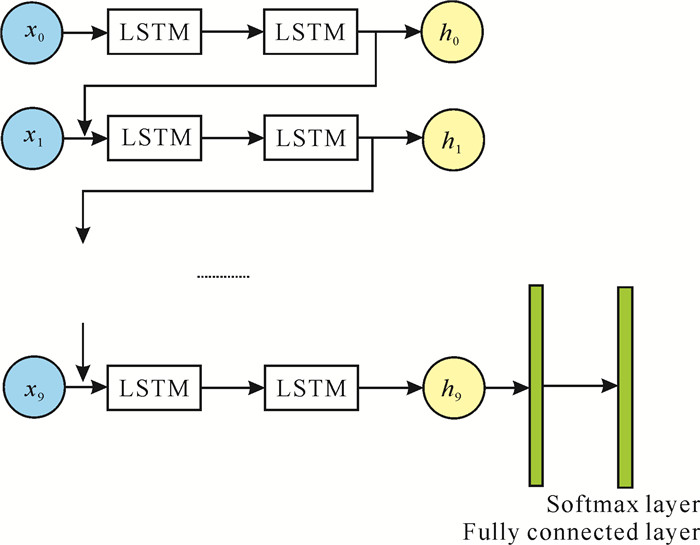
由于呼吸数据具有时间前后关联性,因此可使用LSTM对呼吸数据进行分析,从而判断呼吸是否异常,并将其看作序列分类任务。本研究使用的LSTM单元,接收的输入参数为去噪归一化的呼吸数据,输入的数据是去除基线漂移后并归一化的,吸呼比结合LSTM正常异常分类的LSTM接收的是每呼吸段的吸呼时间比。每个吸呼周期采样32个点,时间窗取10,时间窗内的LSTM提取的时序特征作为一维向量,再连接多层全连接网络进行分类,输出标签为长度为2的one-hot编码形式,(0, 1)表示呼吸异常,(1, 0)表示呼吸正常。则LSTM的网络结构可表示为(320-h1-h2-…-2),其中hi(1≤i≤n)表示第i个隐藏层单元的数量,n为LSTM隐藏层的层数。网络结构设计如图 3所示。
|
| 图 3 LSTM结构 Fig. 3 LSTM structure |
1.5 支持向量机(Support Vector Machine, SVM)
SVM是一种主流的二分类模型,在许多领域都有广泛的应用[10]。SVM将原始数据线性不可分的问题,通过核函数映射到更高维的特征空间中,转化为求解线性约束的二次规划问题。给定训练样本集D=((x1, y1, x2, y2, …, (xm, ym)),yi∈{-1, 1},假设在某个空间能用一个超平面: w·x+b=0,其中w为超平面的法向量方向,b为超平面位移量,决定了超平面与原点之间的距离。该超平面将训练集分为两类,最合适的超平面是最大边距超平面(Maximum-margin hyperplane)[11]。通过求解判别式(7),可得到最佳的w与b的值。
| $ f\left( x \right) = {\rm{sgn}}(\sum\limits_{i = 1}^n {{a_i}{y_i}K\left( {x, {x_i}} \right) + b} ), $ | (7) |
式中,K(x, xi)为核函数,对应于在输入空间构造一个最优的分割平面,ai和b通过SVM学习算法解得[12]。
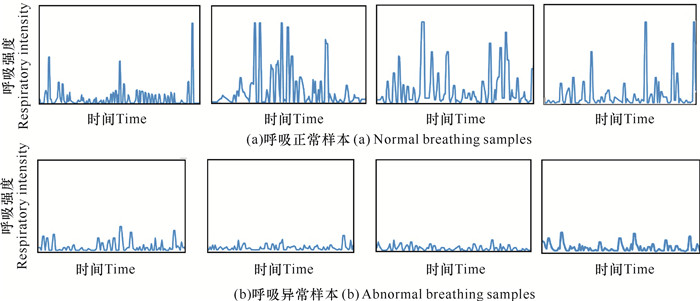
将根据公式(5)计算出的每个吸呼周期的吸呼比进行可视化后(图 4),直接将其归一化为20×20的图片,然后采样为长度为400的一维向量输入SVM中,同时所有的数据被归一化到[0, 1]。实验中,SVM使用的是径向基核函数,其中SVM单个样本的影响范围γ以及模型准确率与模型复杂度平衡参数c均设置为2.0,训练过程采用5折交叉验证。
|
| 图 4 正常、异常吸呼时间比示意图 Fig. 4 Schematic diagram of normal and abnormal breathing time ratio |
2 结果与分析 2.1 数据基线漂移去除处理结果
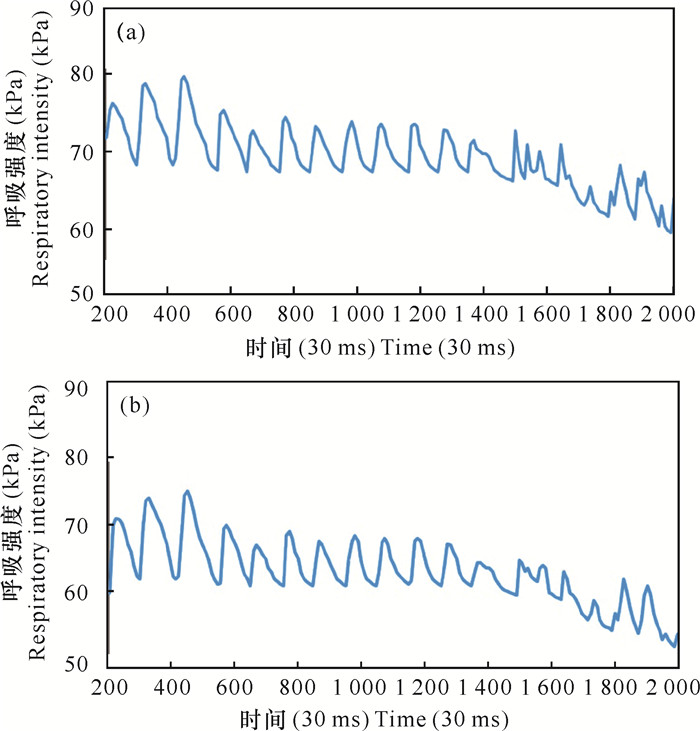
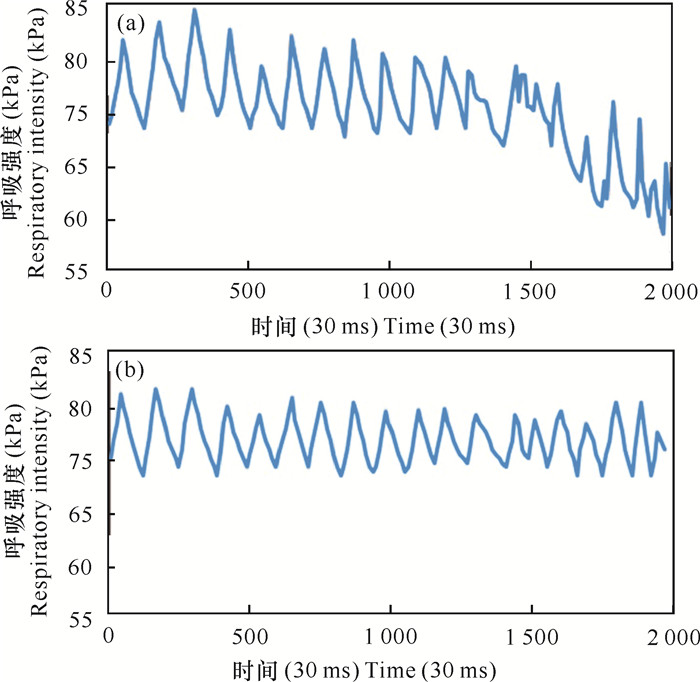
正常、异常呼吸情况下的单个样例信息可视化如图 5所示。可以看到,仅凭借经验难以直接分辨出呼吸正常与异常样本的差距。初始呼吸信号曲线有很多毛刺信息,见图 6(a);进行滤波处理后,50 Hz工频的干扰被滤除,滤波处理后的曲线较初始呼吸信号曲线光滑,见图 6(b),但基线漂移情况仍存在。进一步去除基线漂移处理后,呼吸曲线变换结果如图 7所示,其中图 7(a)为一段没有经过基线漂移处理的呼吸曲线,图 7(b)为图 7(a)经过基线漂移处理的呼吸曲线。对比图 7(a)和图 7(b)可以看到,经过基线漂移处理的呼吸曲线在呼吸强度上的数值随着时间变化更加平稳。

|
| 图 5 呼吸正常与异常数据示例 Fig. 5 Examples of normal and abnormal breathing data |
|
| 图 6 原始呼吸信号(a)和低通滤波处理后的呼吸信号(b) Fig. 6 Original respiratory signal (a) and respiratory signal (b) after low-pass filtering |
|
| 图 7 原始信号(a)及基线漂移去除结果(b) Fig. 7 Original signal (a) and baseline drift removal result (b) |
2.2 3种处理方法的分类精度、召回率以及F-值
对处理后的呼吸数据分别采用LSTM、吸呼比特征+LSTM、吸呼比特征+SVM进行正常呼吸和异常呼吸分类,其分类精度、召回率以及F-值如表 1所示,其中LSTM隐藏层采用不同的神经单元数。可以看到,单纯使用LSTM时分类精度不是很高,为62%左右,其中隐藏单元数为64的效果最好。相对于单纯使用LSTM,吸呼比结合SVM的方法获得的准确度有所提高,达72.8%。吸呼比结合LSTM的方法获得的准确度提升最大,其中吸呼比结合LSTM(320-10-64-64-2)获得的准确度最高,达79.2%,即同时使用64-64两层隐藏层节点时效果最好。
| 方法Methods | 分类精度(%) Classification accuracy (%) | 召回率(%) Recall rate (%) | F-值(%) F-value(%) |
| LSTM(320-10-32-2) | 60.2 | 75.3 | 33.4 |
| LSTM(320-10-64-2) | 63.1 | 78.9 | 35.1 |
| LSTM(320-10-128-2) | 61.5 | 76.9 | 34.2 |
| LSTM(320-10-32-64-2) | 65.4 | 81.7 | 36.3 |
| LSTM(320-10-64-64-2) | 67.8 | 84.7 | 37.7 |
| 吸呼比+SVM Inspiratory/expiratory ratio+SVM | 72.8 | 91.0 | 40.4 |
| 吸呼比+LSTM(320-10-32-2) Inspiratory/expiratory ratio+LSTM(320-10-32-2) | 73.5 | 91.9 | 40.8 |
| 吸呼比+LSTM(320-10-64-2) Inspiratory/expiratory ratio+LSTM(320-10-64-2) | 75.7 | 94.6 | 42.1 |
| 吸呼比+LSTM(320-10-128-2) Inspiratory/expiratory ratio+LSTM(320-10-128-2) | 73.1 | 91.4 | 40.6 |
| 吸呼比+LSTM(320-10-32-64-2) Inspiratory/expiratory ratio+LSTM(320-10-32-64-2) | 76.8 | 96.0 | 42.7 |
| 吸呼比+LSTM(320-10-64-64-2) Inspiratory/expiratory ratio+LSTM(320-10-64-64-2) | 79.2 | 98.9 | 44.0 |
| 吸呼比+LSTM(320-10-64-128-2) Inspiratory/expiratory ratio+LSTM(320-10-64-128-2) | 75.5 | 94.4 | 41.9 |
| 注:LSTM (320-10-32-2) 指LSTM采用四层网络结构,网络输入层、隐藏层和输出层节点分别为10, 32和2 Note:LSTM (320-10-32-2) means that LSTM adopts a four-layer network structure, and the nodes of network input layer, hidden layer and output layer are 10, 32 and 2 respectively | |||
同时可以看到,召回率以及F-值方面,吸呼比结合LSTM(320-10-64-64-2)获得的数值也相对更好,分别达到98.9%和44.0%,比传统的吸呼比inspiratory/expiratory ratio+SVM获得更好的效果。
3 讨论 3.1 方法由上述实验可以看到,采用吸呼比结合SVM的分类方法比单纯采用LSTM的结果更好。一个可能的原因是LSTM完全依靠神经网络提取的特征,而吸呼比特征是目前在临床广泛认可的呼吸是否异常的标准,因此吸呼比特征结合SVM获得了相对于单纯使用LSTM更好的效果。基于这个认识,进一步比较了吸呼比结合LSTM不同网络结构的实验验证,结果发现吸呼比结合LSTM总体获得比吸呼比结合SVM更好的效果。因为LSTM结构的一大特点在于遗忘门机制,并联合上一时刻输出、当前时刻输入、激活函数以及输入门和输出门形成单元状态保持和更换[见公式(6)所描述],其将上/下一个时间步长特征根据一定权值联接到自身,拷贝自身状态的真实值和累积的外部信号,学习到较长时程的吸呼数据的周期性特点。这使得LSTM擅长学习数据间的依赖性,能够提高呼吸带数据在正常、异常分类上的准确率。从表 1的第7行到第12行的数据对比可以看到,更宽和更深的网络相能够提升识别精度,如吸呼比+LSTM(320-10-64-128-2)获得了75.5%的精度,而吸呼比+LSTM(320-10-32-2)以及吸呼比+LSTM(320-10-128-2)精度分别为73.5%和73.1%,相对提高了2.0%和2.4%的准确度,同时在召回率和F-值上也获得提升。然而,也可以看到,针对呼吸带数据,持续地增加网络的宽度和深度并不能一直提高准确度。表 1第12行的吸呼比+LSTM(320-10-64-128-2)相对于第11行的吸呼比+LSTM(320-10-64-64-2)在第3层网络节点数更多,然而其准确度反而比第11行的准确度要低3.7个百分点(79.2%-75.5%)。相似的情况也发生在第12行和第10行的网络结构上。因此,采用合适的网络结构可以获得更佳的判断结果。
3.2 数据获取方法目前,针对呼吸测量的传统方法主要有温度式检测[13]、阻抗式检测、通过获取心电信号然后推断得出呼吸信号等。温度式检测可复用、构成简易,但因为用于测量的传感仪器需要与人体的口鼻腔直接接触,会给被检测者带来不适感[14]。阻抗式检测法是当下在临床中使用较为频繁的呼吸测量方式之一,具有测量稳定、测量方式简单易操作等特点。该方法虽然不会让被检测者产生任何身体不适,具有无创且安全的特性,但是在实施过程中对电极有一定要求,同时会由于血液流动的干扰造成相应比值不易确定等问题[1]。通过获取心电信号然后推断得出呼吸信号,是一种较新颖的无创检测方法,但该方法存在测量的精确度不高,过久地使用心电电极装置可能会给患者的皮肤带来不适等缺点。相对于这些方法而言,呼吸腰带是一种能够长时间使用、无创地对呼吸功能进行测量与评估的方法和工具。
与传统方法相比,使用呼吸腰带有诸多好处:①持续采集,对人体几乎没有伤害。呼吸腰带能直接对患者的呼吸信号进行采集,具有持续性,能连续采集整个时间段里的数据并且不会给患者带来任何创伤。②方便,价格亲民。呼吸腰带使用方便快捷,其中的核心部件包括拉力传感器和数据存储设备,设备大部分功能的实现是将核心部件放置于腰带中,依靠核心部件来检测患者的呼吸信号。目前传感器和数据存储设备的价格并不高,所以整条呼吸腰带的价格比较亲民,能够让大多数患者购置和使用。③信号采集相对稳定。呼吸腰带使用时绑定在患者腰上,有着不错的稳定性;同时患者可以带着它进行大部分的日常活动而不受影响,有良好的舒适性;此外,长时间佩戴和直接检测可提升呼吸数据的精准度。尽管呼吸腰带设备已经面世,但目前尚属于新兴呼吸监测设备,公开报道的文献和研究相对较少[2, 8],且目前对呼吸相关数据的研究分析较少,尤其是对呼吸腰带数据的分析更少。因此,本研究为呼吸腰带长时间、无创地对呼吸功能进行测量与评估提供了一种新的手段和方法。
4 结论为了有效区分呼吸正常与异常人群,本研究采用呼吸腰带采集受试者呼吸数据,并对数据进行预处理后,分别使用LSTM、吸呼比结合LSTM和吸呼比结合SVM进行分类判断,发现吸呼比结合LSTM方法获得的呼吸正常、异常分类效果最好,准确率接近80.0%,相比于单一使用LSTM,其准确率提升15.0%左右,证明该方法的有效性,也为下一步呼吸临床实验、病理检测等提供良好的数据支撑。下一步将考虑使用其他网络结构如递归神经树、随机森林等进行分类判断,并且与医学相关人员进行探讨,寻找吸呼比之外的其他特征,如每次呼吸周期的前斜率、后斜率等,以期得到更好的分类结果。
致谢:
感谢中国医学科学院张启明研究员团队提供呼吸腰带实验数据。
| [1] |
凌振宝, 齐晓慧, 李伟娜, 等. 基于PVDF的呼吸信号检测腰带研究[J]. 压电与声光, 2014, 36(1): 72-75. DOI:10.3969/j.issn.1004-2474.2014.01.018 |
| [2] |
KAUCZOR H U, HAST J, HEUSSEL C P, et al. CT attenuation of paired HRCT scans obtained at full inspiratory/expiratory position: Comparison with pulmonary function tests[J]. European Radiology, 2002, 12(11): 2757-2763. DOI:10.1007/s00330-002-1514-z |
| [3] |
NING T, BRONZINO J D. Automatic classification of respiratory signals[C]//IEEE The Annual International Engineering in Medicine and Biology Society (IEMBS 1989), Seattle, WA, USA: IEEE, 1989.
|
| [4] |
SEBASTIJAN Š, DAMJAN Z. Heartbeat and respiration detection from optical interferometric signals by using a multimethod approach[J]. IEEE Transactions on Biomedical Engineering, 2012, 59(10): 2922-2929. DOI:10.1109/TBME.2012.2213302 |
| [5] |
ALEXANDER T, LYUDMILA K. Sleep stage classification based on respiratory signal[C]//IEEE 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy: IEEE, 2015.
|
| [6] |
AGNEL J K J, PAMELA D. Arduino uno based obstr- uctive sleep apnea detection using respiratory signal[J]. International Journal of Research in Engineering and Technology, 2015, 4(3): 599-603. DOI:10.15623/ijret.2015.0403100 |
| [7] |
RAJI A, DEVI P K, JEYASEELI P G, et al. Respiratory monitoring system for asthma patients based on IoT[C]//IEEE 2016 Online International Conference on Green Engineering and Technologies (IC-GET), Coimbatore, India: IEEE, 2016.
|
| [8] |
陈苹, 叶继伦, 张旭, 等. 心电信号中基线漂移的去除方法比较及算法实现[J]. 中国医疗器械杂志, 2018, 42(5): 326-329. DOI:10.3969/j.issn.1671-7104.2018.05.004 |
| [9] |
DUNLAP J C. Molecular bases for circadian clocks[J]. Cell, 1999, 96(2): 271-290. DOI:10.1016/S0092-8674(00)80566-8 |
| [10] |
SCHULDT C, LAPTEV I, CAPUTO B. Recognizing human actions a local SVM approach[C]//IEEE Proceedings of the 17th International Conference on Pattern Recognition(ICPR2004), Cambridge, UK: IEEE, 2004.
|
| [11] |
LEANDERS S, LAGUNA P, SORNMO L. Estimation of the respiration frequency using spatial inform action in the VCG[J]. Medical Engineering Physics, 2003, 25(6): 501-507. DOI:10.1016/S1350-4533(03)00017-1 |
| [12] |
VAPNIK V N. Statistical learning theory[M]. New York: Wiley-Interscience, 1998.
|
| [13] |
范霖, 陈向东, 李宁. 基于快速响应湿度传感器的无线呼吸检测系统[J]. 传感器与微系统, 2015, 34(3): 84-86. |
| [14] |
吴丹, 徐效文, 王磊, 等. 穿戴式动态睡眠呼吸监测系统的设计[J]. 传感技术学报, 2010, 23(3): 322-325. DOI:10.3969/j.issn.1004-1699.2010.03.007 |



