2. 华南师范大学, 数据科学与工程学院, 广东汕尾 516600
2. School of Data Science & Engineering, South China Normal University, Shanwei, Guangdong, 516600, China
现实生活中涌现出越来越多的多目标优化问题(Multi-objective Optimization Problem,MOP),但是这些目标之间通常是相互制约的,一个目标在得到改善的同时会伴随着其他目标的效果变差,故MOP得到的解不能同时满足全部目标最优,而是一组折衷的解,即Pareto解集或非劣解集[1]。基于群体搜索的进化算法(Evolutionary Algorithm,EA)是模拟生物进化过程的自组织、自适应的人工智能技术,主要通过选择、交叉、变异、重组等遗传操作求解问题,其最大的优势就是不要求问题满足连续、可微等特定性质。基于EA求解MOP问题的优势,短短数年内涌现出大量优秀的多目标进化算法(Multi-objective Evolutionary Algorithm,MOEA)。
1985年由Schaffer提出的矢量评价遗传算法VEGA[2]是最早的进化算法。在此后的时间里,学者针对不同的优化问题提出不同的MOEA,其中最具代表性的算法是以Pareto支配为基础的MOEA,如NSGA[3]、NSGA-2[4]、强度Pareto进化算法SPEA[5]、SPEA2[6]和PESA-Ⅱ[7]等。上述算法在求解较少数目标优化问题上表现出良好的性能,其中以NSGAⅡ最具代表性。
多目标优化问题在现实生活中的应用比比皆是,例如:电力供应[8]、海水淡化[9]、护士排班问题[10]、汽车控制器优化问题[11]以及疫情救灾点优化[12]等。这些实际应用问题的目标数通常是大于等于4的,所以这些问题又被称为高维多目标优化问题(Many-objective Optimization Problem,MaOP)。MaOP在传统的优化过程会面临很多困难,如:①随着目标数的增加,种群中非支配个体所占的比例会急剧增大,严重削弱Pareto选择压力;②在目标空间中可能会出现偏远的解,即支配抵触解(Dominance Resistance Solution,DRS)[13];③在高维空间中,因为个体可能相距太远,父代产生的子代有很大的差异,导致后代不稳定且不具有代表性,通常会面临杂交和变异算子失效的情况[14];④Pareto前沿面表示困难。假设有m个目标的优化问题,每个目标上有b个解,则共需要mbm-1个解表示,这在现实应用中十分困难。MaOP算法的提出一般基于上述几个问题,提出针对性的解决方案。
传统的NSGAⅡ算法在高维(目标数大于等于4)目标空间优化时,算法性能急剧下降,且算法的多样性表现较差,不适用于现在的多目标优化问题。受Elarbri等[15]所提出的RPD-NSGAⅡ启发,本研究采用d2距离来增强算法在高维空间的多样性,提出算法d2-NSGAⅡ。新算法拟在保证NSGAⅡ原有精英策略等优点的同时,显著改善算法的分布性。
1 多目标优化问题及相关概念统一以最小化问题为例,将m个目标函数和n个决策变量,(p+q) 个约束的MOP描述为
| $ \left\{ \begin{array} { l } { \operatorname { min } y = F ( x ) = ( f _ { 1 } ( x ) , f _ { 2 } ( x ) , \cdots , f _ { m } ( x ) ) } \\ { x = ( x _ { 1 } , x _ { 2 } , \cdots , x _ { n } , ) } \\ { y = ( y _ { 1 } , y _ { 2 } , \cdots , y _ { n } , ) } \\ { s . t . g _ { i } ( x ) \geq 0 , i = 1, 2 , \cdots , p } \\ { h _ { j } ( x ) = 0 , j = 1, 2 , \cdots , q } \end{array} \right.,$ | (1) |
式中x∈X⊂Rn,y∈Y⊂Rm,n是决策变量的个数,m是目标向量的个数,x表示决策向量,X是由决策向量x形成的决策空间;y表示目标向量,Y是由目标向量形成的目标空间;F(x)定义了由决策空间X向目标空间Y映射的函数,g(x)定义了p个不等式约束,h(x)定义了q个不等式约束。
定义 1 (可行解集)满足式(1)中约束函数的决策向量的集合,用Xl表示,Xl={ x∈X g(x)≥0∧h(x)=0}。
定义 2 (Pareto支配)存在x1, x2∈Xl是问题的解,当满足∀i∈(1, …M): fi(x1)≤fi(x2)∧∃j∈(1, …M): fi(x1) < fi(x2)时候,称x1 Pareto支配x2(记为x1
定义 3 (Pareto最优解)当不存在其他解x∈Xl,使得x
定义 4 (Pareto最优解集)满足定义3的解的集合称为Pareto最优解集(Pareto optimal set,PS),表示为PS={xl}={x∈Xl|-∃x′∈Xl: x′
定义 5 (Pareto前沿) PS在目标空间的投影叫做Pareto前沿(Pareto optimal front,PF),表示为PF={F(x)∈Rm|x∈PS}。
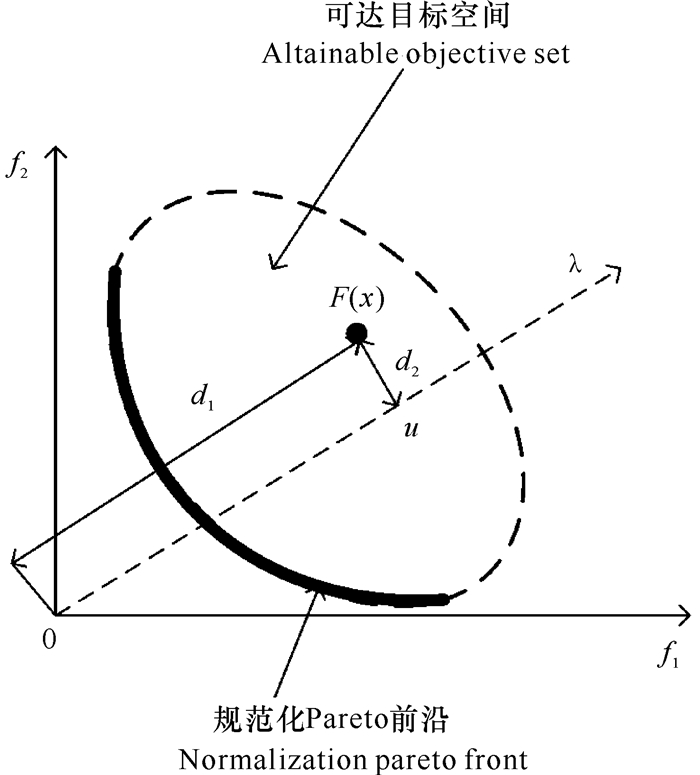
多目标进化算法按照不同优化标准可以分为3类:基于支配的MOEA、基于指标的MOEA以及基于分解的MOEA。其中,基于支配的MOEA算法代表有NSGAⅡ和SPEA2,基于分解的MOEA算法代表有MOEA/D[16]、MOEA/D-URAW[17]以及MOEA/D-DRA[18],基于指标的MOEA算法代表有超体积评价指标(Hypervolume,HV)[19]、MOEA-HV[20]以及基于R2指标的R2-HVC[21]。在基于分解的MOEA算法中,Zhang与Li[16]于2007年提出了一种优秀的PBI分解方法,该方法因为可以较好地控制种群的收敛性和分布性而广受关注。PBI在应用时需要度量两个距离d1和d2,d1代表解在参考向量方向投影距离原点的欧式距离,d2代表解距离参考向量的欧式距离,具体度量如图 1所示。通过图示不难看出,一个较小的d1代表解距离PF近,个体的收敛性更好;同样较小的d2代表解具有更好的多样性,当d2=0时,意味着解在参考向量的方向上。
|
| 图 1 d1与d2距离的度量 Fig. 1 Measure of the distance of d1 and d2 |
具体数学表示如公式(2):
| $ \left\{ \begin{array}{l} {d_1}\left( x \right) = \left\| {f{{\left( x \right)}^{\rm{T}}}\lambda } \right\|/\left\| \lambda \right\|\\ {d_2}\left( x \right) = \left\| {f\left( x \right){\rm{ - }}{{\rm{d}}_1}\left( x \right)\left( {\frac{\lambda }{{\left\| \lambda \right\|}}} \right)} \right\| \end{array} \right., $ | (2) |
其中f(x)= f1(x), f2(x), …, fm(x)T是解x的标准目标向量,PF是真实前沿面,λ是m维的方向向量。
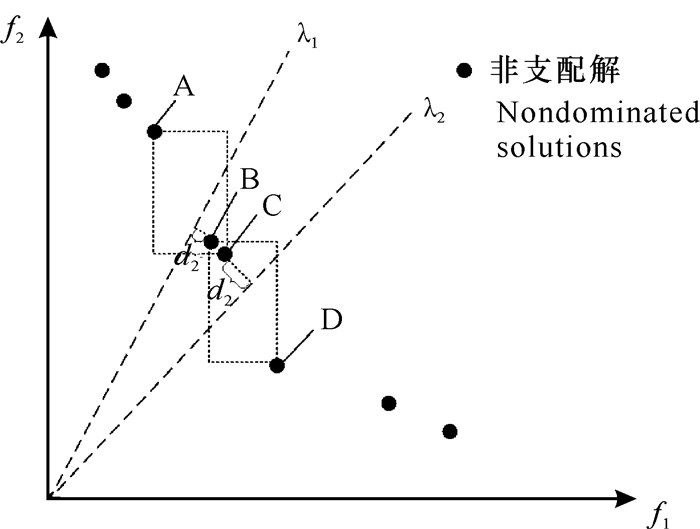
2 基于d2距离的改进型NSGAⅡ传统的NSGAⅡ算法在保持种群多样性方面采用的是度量拥挤距离,该方法存在一定缺陷,即欧氏距离的度量在高维空间中不再适用[22]。个体的拥挤距离存在不能准确度量个体拥挤度的问题, 在种群迭代的时候,该问题会导致分布性差的个体反而被保留,进而导致种群多样性较差。如图 2所示,图中个体为最后非支配层的个体,个体B、C的拥挤距离较大且相等,在迭代的时候这两个个体会被保留下来。但是,由图 2可以看出这两个个体实际距离较为接近,不应该全部被保留;此时根据拥挤距离不能确定个体,可以度量两个个体距离相应权重向量的d2距离,选择距离小的个体保留(保留个体B)。
|
| 图 2 种群个体分布图 Fig. 2 Distribution of population individuals |
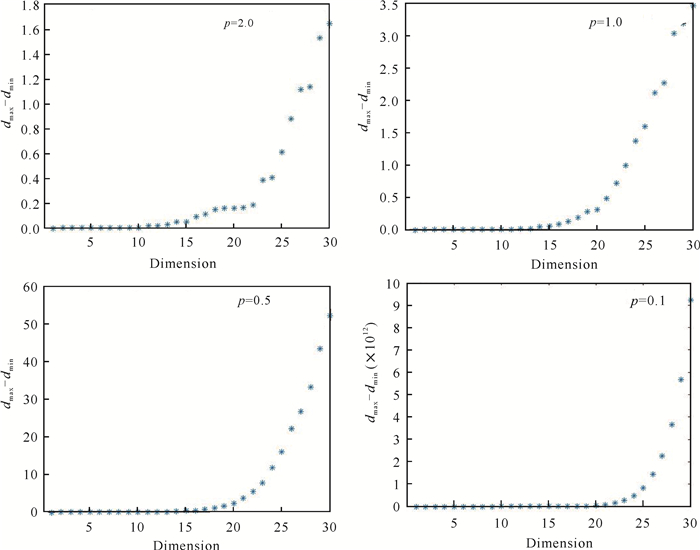
设置对照实验,增加统一数据集的维数,计算出目标空间中最近与最远个体之间的差值dmax-dmin,实验参数设置如下:目标数M=30,决策变量数目D=30,种群数N=100,评价次数Evaluation=10 000,p分别取值2.0,1.0,0.5,0.1。通过实验数据(图 3)可以看出,当p=2.0(欧氏距离)以及p=1.0(曼哈顿距离)时,在高维空间dmax与dmin差值不是很明显; 当p=0.5以及p=0.1时,随维数的增加,dmax与dmin差值明显变大,有利于在高维空间中选择分布性较好的个体保留。因此,欧式距离降低了在高维空间中多样性的选择能力,其在高维空间中意义不大。相反地,其他p范式距离(p < 1) 在高维空间上表现更好。
|
| 图 3 不同p取值下dmax与dmin差值变化情况 Fig. 3 Variation between dmaxand dmin under different values of p |
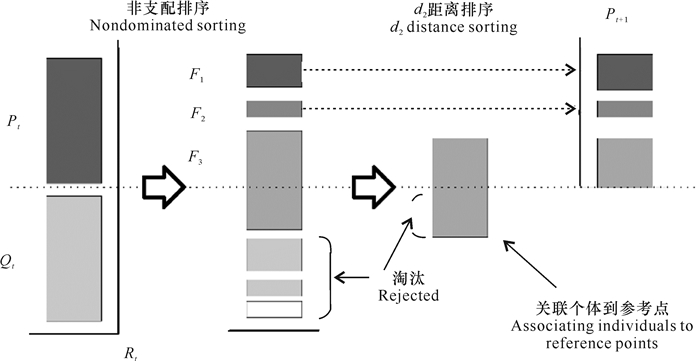
Pareto支配能更好地提高算法的收敛性,而PBI效用函数的d2距离可以提高种群的多样性分布。为将二者结合并求解高维目标优化问题,本研究将d2距离的度量应用到NSGAⅡ框架中。同样采用NSGAⅡ非支配排序的方法选择优秀个体,保留F1, F2…Fl-1非支配层个体,删除Fl层以后的个体,在第Fl非支配层利用个体距离相应参考向量的d2距离,选择出剩余优秀个体,使得种群规模保持不变。这样在保证种群收敛性的同时,促进种群的多样性。由此,产生一种基于d2距离的新算法d2_NSGAⅡ,算法的示意如图 4所示。
|
| 图 4 d2_NSGAⅡ示意图 Fig. 4 Schematic diagram of the d2_NSGAⅡ |
算法中使用的Pareto支配满足反自反、反对称和传递性质。
① 反自反性:种群中任一个体x,满足反自反性,即x-
证明:如果x
② 反对称性:种群中任意两个体x,y如果满足x
证明:假设x
③ 传递性:x, y, z是种群中3个个体,如果x
证明:因为x
除非支配排序外,文章还涉及参考点的产生。因文章算法针对高维多目标优化问题,因此采用Deb和Jain的双层参考点产生方法,产生两层参考点,每层参考点数量计算公式相同,具体如下所示:
| $ C = \left( \begin{array}{l} H + M - 1\\ M - 1 \end{array} \right), $ | (3) |
其中,C代表参考点数量,M代表目标数量,H代表超平面上沿着每个目标考虑的划分数量。
假设在一个3目标优化问题上,在外层参考点上,取H1=2,则外层参考点数目C1=

|
| 图 5 参考向量的产生以及参考点的分布 Fig. 5 Generation of reference vectors and distribution of reference points |
| 目标数目 Objectives (M) |
参数设置 Parameters setting (H1,H2) |
参考点数目 Reference points (C) |
| 3 | H1=12, H2=0 | 91 |
| 5 | H1=6, H2=0 | 210 |
| 8 | H1=3, H2=2 | 156 |
| 10 | H1=3, H2=2 | 275 |
| 15 | H1=2, H2=1 | 135 |
d2_NSGAⅡ具有以下特点:①利用NSGAⅡ经典框架,保留精英策略,同时采用非支配排序,算法时间复杂度低;②算法最后的非支配层采用d2距离度量,可以在收敛性的基础之上最大化地提高多样性。以下给出算法的具体流程。
算法:d2_NSGAⅡ算法
输入:种群规模N,决策变量数目D,MaOP问题的目标数目M,最大迭代次数Tmaxgen,沿目标方向划分H份
输出:最末代种群Pmaxgen
1.初始化
1.1初始化迭代计数器t=0;
1.2在MaOP问题的可行决策空间内随机产生N个初始点,形成初始化种群P0;
1.3计算P0中所有解的目标值向量F1(0), …, FN(0);
1.4产生参考点(M, H)→Set;
2.WHILE(t < Tmaxgen)
3.构建交配池:Ptmating=Mating_selection(Pt);
4.重组运算:Ptrecombination=Recombination(Ptmating);
5.变异运算:Ptoffspring=Mutation(Ptrecombination);
6.合并子种群和父种群:Rt=Pt∪Qt;
7.计算最小向量值→Fmin;
8.计算最大向量值→Fmax;
9.归一化处理(Rt, Fmin, Fmax)→Rt;
10.保留Rt中边界解;
11.对Rt集合中的个体进行非支配排序;
12.确定最小的k值,使其满足|F1∪F2∪…∪Fk|≥N; //Fi表示第i层非Pareto支配层;
13.计算非支配层(Fk)个体的d2距离d2(Fk, Set);
14.关联Fk中个体与Set集合中的点;
15.IF |F1∪F2∪…∪Fk|>N THEN
16.根据距离从非Pareto支配层Fk中删除(|F1∪F2∪…∪Fk|-N)个具有较大d2距离的个体;
17.END IF
18.Pt+1=|F1∪F2∪…∪Fk|;//获得规模为N的下一代种群;
19.更新迭代计数器t=t+1;
20.END WHILE.
21.输出最末代种群Pmaxgen。
算法的第1步为初始化,随机产生个体,并计算其目标值大小,同时产生参考点;第2步进入循环,进行重组变异,产生新的后代;第3步Mating_selection利用二元竞标赛法选取优秀的N/2个体;第4步对交配池中的个体进行仿二进制交叉(SBX),得到规模为N的种群Ptrecombination;第5步执行变异操作,得到后代Qt,规模为N。然后进行父种群以及子代种群的合并,生成规模为2N的新种群。为了便于目标值的比较,对目标值进行归一化处理。
归一化的目的是为了消除个体极端目标值,将数据标准化,便于比较,使实验数据更加可靠真实。首先,确定种群中个体每个目标分量fi的最小值fimin,构造向量Fmin= f1min, f2min, …, fMmin T,同样构造目标最大值的向量Fmax= f1max, f2max, …, fMmax T,其中fimax是种群Rt中fi的最大值。然后将Rt中所有个体目标值归一化,具体归一化公式如下所示:
| $ {{\bar f}_i}(x) = \frac{{{f_i}(x) - f_i^{{\rm{ min }}}}}{{f_i^{{\rm{ max }}} - f_i^{{\rm{ min }}}}}{\rm{ }}。$ | (4) |
算法第13步通过公式(2)计算Fk层个体距离参考向量的d2距离,找到距离个体最近的参考向量进行关联。如图 6所示,度量个体a、b、c、e所有权重向量的d2距离,不难发现,个体b距离参考向量λ1最近,个体c距离参考向量λ2最近,将Fk层个体与相应权重向量关联。算法中,先进性非支配排序获得若干非支配层后,再对Fk非支配个体进行关联参考点,这样可以避免计算所有个体的d2距离,减少计算复杂度。

|
| 图 6 个体关联参考点 Fig. 6 Individuals associated with reference points |
同时,保留目标空间中的边界值,将在每个目标上的最大值与最小值的个体保留下来(边界值)。将边界个体的d2值设置为0,在迭代的时候将d2值为0的个体保留下来。与NSAGⅡ同样地进行非支配排序,确定最后的非支配层使得种群规模保持N,并在最后非支配层根据d2值由小到大筛选优秀的个体,使种群的规模保持为N,进入下一代迭代。
d2_NSGAⅡ的时间复杂度主要由两部分组成:非支配排序、d2距离度量。假设MOP有M个目标,种群规模N。非支配排序中,种群中所有个体之间相互比较,确定所有个体计数Sq(被个体q支配的个体数目) 和个体q支配的个体数目nq,需要两两个体比较,时间复杂度为O(MN2)。在找到第一非支配层个体后,剩余个体的nq计数最多为N-1,故剩余个体最多需要遍历(N-1)次才会找到所在非支配层。因为除去第一非支配层之外最多剩余个体为(N-1),故此过程时间复杂度为O(N2)。因此,非支配排序的时间复杂度为O(MN2)。在最差情况下,即第一非支配层即为最后非支配层,需度量所有个体距离参考向量的距离,时间复杂度为O(N2)。综上两部分时间复杂度比较,取最高次幂,故d2_NSGAⅡ的时间复杂度为O(MN2)。
3 测试实验与数据分析为验证所提出的d2_NSGAⅡ算法的有效性,采用3组对比算法在DTLZ系列测试函数上进行实验数据的对照以及分析,所采用的算法依次是NSGAⅡ、NSGA、VaEA[23]、MOEAD以及MOEADFFRMAB[24]。
3.1 测试问题研究采用的是DTLZ系列测试函数,具体为DTLZ1-DTLZ7。DTLZ测试函数的前沿面具有多样性,具备不同的特征,可以从多个角度检验算法在高维多目标情况下优化问题的能力,而且采用的测试函数在目标空间和决策空间上均具有可扩展性。DTLZ系列测试函数的具体特征描述如表 2所示。
| 测试问题 Test problems |
特征描述 Characteristics description |
| DTLZ1 | 线性、多模态Linear, multimodal |
| DTLZ2 | 凹型Concave |
| DTLZ3 | 凹型、多模态Concave, multimodal |
| DTLZ4 | 凹型、有偏Concave, biased |
| DTLZ5 | 连续均匀曲线Continuous uniform curve |
| DTLZ6 | 连续均匀曲线Continuous uniform curve |
| DTLZ7 | 不连续、多模态、比例缩放Discontinuous, multimodal, proportional scaling |
3.2 性能指标
采用IGD指标测试新算法的性能。该指标反映了真实的Pareto前沿到近似Pareto前沿之间的距离,可以综合度量算法的收敛性与多样性。IGD指标具体工作机制如下:在真实的Pareto前沿上采用一组分布较为均匀的点,并计算他们到近似Pareto解之间的距离。IGD指标的值越小表明算法收敛性与多样性越好。具体的计算公式如下:
| $ {\rm{IGD}} = \frac{1}{{|P|}}\sum\limits_{i = 1}^{|P|} { Dist{ _i}} , $ | (5) |
| $ {\rm{Dis}}{{\rm{t}}_i} = \mathop {min}\limits_{j = 1}^{\left| A \right|} \sqrt {{{\sum\limits_{m = 1}^M {(\frac{{{f_m}({p_i}) - {f_m}({a_j})}}{{f_m^{ max } - f_m^{ min }}})} }^2}} , $ | (6) |
上述公式中,P是MOP问题的解集;Disti是目标函数归一化处理之后的最小欧氏距离;fmmax和fmmin分别表示P在第m个目标上获得的最大值与最小值。A为近似Pareto前沿,pi∈P, i=1, 2, …, |P|;aj∈A, j=1, 2, …, |A|。在对比实验中,实验进行30次,取结果平均值作为最后的实验结果;同时利用显著水平为0.05的Wilcoxon秩和检验分析所有对比算法结果的差异。
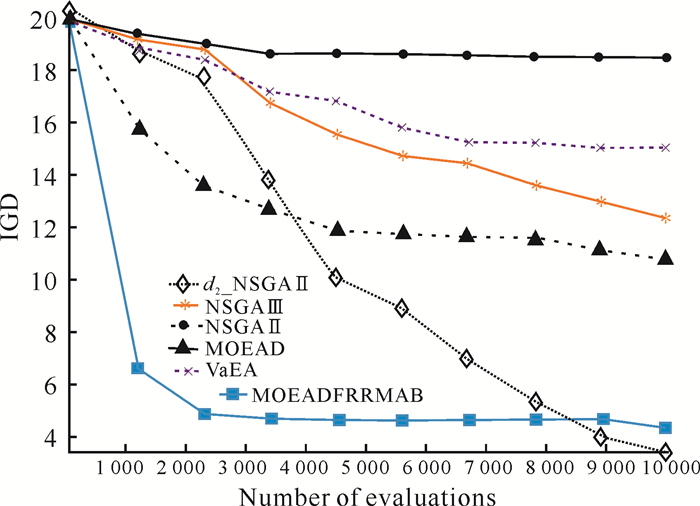
3.3 实验结果与分析实验对比了6种算法在DTLZ6测试函数上,目标数为8的IGD值变化情况(图 7)。从图 7可以看出,随着评估次数的增大,6种算法的IGD值整体在变小。评估次数在3 000之前,d2_NSGAⅡ的下降速度远远大于NSGAⅡ、VaEA、NSGAⅢ,但是稍微小于MOEAD和MOEADFRRMAB;评估次数在3 000之后,d2_NSGAⅡ的下降速度仅仅略逊色于MOEADFRRMAB,但是远远超过其他4种算法。图 7算法的IGD变化情况印证了d2_NSGAⅡ算法在算法多样性与收敛性方面的效果。
|
| 图 7 6种算法在DTLZ6测试函数上(目标数为8)的IGD值变化 Fig. 7 Change of IGD values of 6 algorithms on DTLZ6 test function (target number 8) |
表 3给出d2_NSGAⅡ与NSGAⅡ、NSGAⅢ、VaEA、MOEAD、MOEADFRRMAB 6种算法在测试函数上的IGD值,以及他们的优劣对比,表现优秀的IGD值用加粗字体标注。将目标数分别设置为3, 5, 8, 10 (表 3),在28组测试函数中,d2_NSGAⅡ共取得7个最佳IGD值,NSGAⅡ共获得1个最佳IGD值,VaEA取得1个最佳值,NSGAⅢ共取得4个最佳IGD值,MOEAD共取得11个最佳IGD值,MOEADFRRMAB取得4个最佳IGD值。从表中的Wilcoxon秩和检验结果看,相比于MOEAD、MOEADFRRMAB、VaEA、NSGAⅢ、NSGAⅡ,d2_NSGAⅡ净胜得分(数据优于对比算法的个数减去差于对比算法的个数)为-2, 0, 6, 1, 16。由此可见,除算法性能稍微劣于MOEAD、MOEADFRRMAB,d2_NSGAⅡ均优于其他几种算法,故认为d2_NSGAⅡ算法在求解DTLZ系列测试函数具有较为优秀的性能。
| Problem | M | d2_NSGAⅡ | MOEAD | MOEADFRRMAB | VaEA | NSGAⅢ | NSGAⅡ |
| DTLZ1 | 3 | 5.3733e+ 1(1.16e+1) | 4.9855e+ 1(1.31e+1) = | 5.0322e+ 1(3.47e+1) = | 8.2390e+ 1(1.51e+1)↓ | 8.2733e+ 1(1.57e+1)↓ | 5.4695e+ 1(1.26e+1) = |
| 5 | 8.1375e+ 1(1.59e+1) | 3.8626e+ 1(9.89e+0)↑ | 5.6873e+ 1(3.87e+1)↑ | 1.0865e+ 2(1.92e+1)↓ | 9.9737e+ 1(1.56e+1)↓ | 3.0365e+ 2(6.05e+1)↓ | |
| 8 | 2.0815e+ 1(5.33e+0) | 6.6281e+ 1(2.19e+1)↓ | 3.9894e+ 1(3.85e+1)↓ | 1.2781e+ 2(2.23e+1)↓ | 6.3370e+ 1(1.48e+1)↓ | 5.4696e+ 2(6.75e+1)↓ | |
| 10 | 5.6325e+ 1(1.99e+1) | 1.3428e+ 1(4.82e+0)↑ | 3.4889e+ 1(2.42e+1)↑ | 1.0247e+ 2(1.62e+1)↓ | 5.6127e+ 1(1.26e+1) = | 4.9799e+ 2(7.61e+1)↓ | |
| DTLZ2 | 3 | 1.5199e- 1(1.79e-2) | 6.4252e- 2(3.31e-3)↑ | 2.8685e- 1(4.90e-2)↓ | 6.4185e- 2(2.48e-3)↑ | 6.2138e- 2(1.63e-3)↑ | 7.8172e- 2(2.79e-3)↑ |
| 5 | 2.5974e- 1(1.35e-2) | 2.2182e- 1(4.00e-3) = | 7.6490e- 1(5.90e-2)↓ | 7.4503e- 1(8.33e-2)↓ | 2.4910e- 1(7.98e-3)↑ | 7.7339e- 1(1.70e-1)↓ | |
| 8 | 1.0228e+ 0(8.50e-2) | 3.9734e- 1(7.87e-3)↑ | 9.4599e- 1(5.81e-2)↑ | 6.5144e- 1(6.18e-2)↑ | 4.7902e- 1(6.88e-2)↑ | 2.5330e+ 0(4.52e-1)↓ | |
| 10 | 1.0016e+ 0(8.95e-2) | 6.0248e- 1(6.29e-2)↑ | 1.0263e+ 0(6.36e-2) = | 7.9870e- 1(6.52e-2)↑ | 6.3599e- 1(5.00e-2)↑ | 2.3655e+ 0(3.07e-1)↓ | |
| DTLZ3 | 3 | 1.3251e+ 2(2.77e+1) | 1.6589e+ 2(3.92e+1)↓ | 1.8165e+ 2(1.25e+2) = | 2.0105e+ 2(3.47e+1)↓ | 2.2824e+ 2(3.80e+1)↓ | 1.3364e+ 2(3.39e+1) = |
| 5 | 2.7516e+ 2(5.13e+1) | 1.5275e+ 2(2.89e+1)↑ | 1.4727e+ 2(1.13e+2)↑ | 3.3270e+ 2(5.69e+1)↓ | 2.8932e+ 2(4.62e+1) = | 8.2180e+ 2(1.31e+2)↓ | |
| 8 | 1.0467e+ 2(3.92e+1) | 1.2567e+ 2(2.90e+1)↓ | 1.2406e+ 2(1.01e+2)↓ | 5.0577e+ 2(7.52e+1)↓ | 2.4656e+ 2(4.47e+1)↓ | 2.3636e+ 3(2.51e+2)↓ | |
| 10 | 6.5087e+ 1(2.50e+1) | 7.6939e+ 1(2.00e+1)↓ | 8.5980e+ 1(7.53e+1)↓ | 4.2819e+ 2(5.86e+1)↓ | 2.2353e+ 2(5.86e+1)↓ | 2.1303e+ 3(3.39e+2)↓ | |
| DTLZ4 | 3 | 1.6098e- 1(1.94e-1) | 4.9974e- 1(3.92e-1)↓ | 5.2833e- 1(1.96e-1)↓ | 4.7682e- 1(1.70e-1)↓ | 2.4773e- 1 (3.05e-1)↓ | 3.5211e-1 (2.80e-1)↓ |
| 5 | 2.8046e- 1 (2.03e-2) | 7.5770e- 1(2.57e-1)↓ | 7.5919e- 1 (1.19e-1)↓ | 7.4473e- 1 (6.18e-2)↓ | 3.5523e- 1 (1.15e-1)↓ | 5.7664e- 1 (1.11e-1)↓ | |
| 8 | 6.5776e- 1 (5.05e-2) | 8.9577e- 1 (1.92e-1)↓ | 9.1988e- 1 (5.32e-2)↓ | 9.2083e- 1 (7.70e-2)↓ | 5.7650e- 1 (7.52e-2)↑ | 2.4329e+ 0 (3.60e-1)↓ | |
| 10 | 1.0426e+ 0 (7.11e-2) | 1.0436e+ 0 (1.78e-1) = | 9.7840e- 1 (4.36e-2)↑ | 8.0668e- 1 (3.88e-2)↑ | 6.5001e- 1 (6.11e-2)↑ | 2.1652e+ 0 (1.72e-1)↓ | |
| DTLZ5 | 3 | 6.9697e- 2 (6.77e-3) | 2.9184e- 2 (1.60e-3)↑ | 1.0675e- 1 (4.18e-2)↓ | 1.8283e- 2 (3.67e-3)↑ | 1.9973e- 2 (2.51e-3)↑ | 1.2514e- 2 (2.03e-3)↑ |
| 5 | 6.5578e- 1 (1.37e-1) | 2.4457e- 2 (2.86e-3)↑ | 2.1652e- 1 (6.51e-2)↑ | 3.2050e- 1 (4.10e-2)↑ | 3.1531e- 1 (5.24e-2)↑ | 9.6093e- 1 (1.95e-1)↓ | |
| 8 | 2.9246e- 1 (5.35e-2) | 6.2137e- 2 (1.49e-2)↑ | 4.0029e- 1 (7.95e-2)↓ | 6.7726e- 1 (1.23e-1)↓ | 6.2208e- 1 (1.17e-1)↓ | 1.5987e+ 0 (3.37e-1)↓ | |
| 10 | 6.1807e- 1 (1.36e-1) | 7.9997e- 2 (1.12e-2)↑ | 2.5732e- 1 (4.67e-2)↑ | 7.0154e- 1 (1.75e-1) = | 3.3652e- 1 (4.80e-2)↑ | 1.7129e+ 0 (3.55e-1)↓ | |
| DTLZ6 | 3 | 4.7408e+ 0 (1.34e+0) | 8.2580e+ 0 (1.77e+0)↓ | 1.5862e- 1 (4.37e-1)↑ | 3.6819e+ 0 (8.65e-1)↑ | 4.2542e+ 0 (1.02e+0) = | 4.4193e+ 0 (1.35e+0) = |
| 5 | 7.4818e+ 0 (1.36e+0) | 1.0129e+ 1 (1.59e+0)↓ | 1.5845e+ 0 (1.75e+0)↑ | 1.5943e+ 1 (1.05e+0)↓ | 1.3469e+ 1 (8.84e-1)↓ | 1.9596e+ 1 (8.82e-1)↓ | |
| 8 | 1.2460e+ 0 (7.35e-1) | 8.3860e+ 0 (1.80e+0)↓ | 5.7767e+ 0 (1.50e+0)↓ | 1.4326e+ 1 (9.03e-1)↓ | 1.3569e+ 1 (1.02e+0)↓ | 1.8562e+ 1 (8.06e-1)↓ | |
| 10 | 3.9380e+ 0 (1.12e+0) | 4.7311e+ 0 (1.85e+0) = | 4.3927e- 1 (5.07e-1)↑ | 1.2974e+ 1 (7.75e-1)↓ | 1.2650e+ 1 (9.26e-1)↓ | 1.7336e+ 1 (6.57e-1)↓ | |
| DTLZ7 | 3 | 1.5616e- 1 (4.04e-2) | 1.4396e- 1 (1.86e-2)↑ | 5.7350e- 1 (9.75e-2)↓ | 1.2356e- 1 (2.05e-2) = | 4.7374e- 1 (1.16e-1)↓ | 1.3477e- 1 (2.01e-2) = |
| 5 | 1.0672e+ 0 (2.01e-1) | 2.7553e+ 0 (1.56e-1)↓ | 1.0383e+ 0 (1.67e-1) = | 5.9338e- 1 (6.94e-2)↑ | 5.8097e- 1 (1.07e-1)↑ | 8.6364e- 1 (8.80e-2)↑ | |
| 8 | 1.9351e+ 1 (2.47e+0) | 1.5686e+ 0 (2.13e-1)↑ | 2.8765e+ 0 (1.38e+0)↑ | 1.6587e+ 0 (2.00e-1)↑ | 4.2727e+ 0 (1.14e+0)↑ | 7.0155e+ 0 (1.90e+0)↑ | |
| 10 | 1.2169e+ 1 (2.54e+0) | 2.0851e+ 0 (3.40e-1)↑ | 2.1327e+ 0 (1.41e+0)↑ | 2.3289e+ 0 (3.72e-1)↑ | 4.6105e+ 0 (1.03e+0)↑ | 2.4191e+ 1 (3.03e+0)↓ | |
| ↑/↓/= | 13/11/4 | 12/12/4 | 10/16/2 | 12/13/3 | 4/20/4 | ||
| 注:“↑”“↓”和“=”分别表示该结果显著地优于、劣于和统计上无差别于d2_NSGAⅡ算法 Note: "↑", "↓", and "=" indicate that the result is significantly better, worse and similar to that obtained by d2_NSGAⅡ algorithm | |||||||
4 结论
为解决NSGAⅡ在高维空间中效果不佳的问题,研究提出基于d2距离的NSGAⅡ算法,在保证算法收敛性的同时增加其多样性。通过实验数据验证,该算法在MaOP上取得了不错的效果,但是随着目标数目的增加,算法性能下降。究其原因,随着目标数目的增加,个体之间变得相互非支配,这是传统非支配方法面临的统一问题。未来可从支配关系以及距离度量方面进一步改进与探索,同时可以设计一些更加复杂的MaOP问题检验算法的有效性,使其效果更加优秀。
| [1] |
公茂果, 焦李成, 杨咚咚, 等. 进化多目标优化算法研究[J]. 软件学报, 2009, 20(2): 271-289. |
| [2] |
SCHAFFER J D. Multiple objective optimization with vector evaluated genetic algorithms[C]// GREFENSTETTE J J. Proceedings of the 1st International Conference on Genetic Algorithms, Pittsburgh, PA, USA, July 1985. Hillsdale: Lawrence Erlbaum Associates Publishers, 1985: 93-100.
|
| [3] |
SRINIVAS N, DEB K. Muiltiobjective optimization using nondominated sorting in genetic algorithms[J]. Evolutionary Computation, 1994, 2(3): 221-248. DOI:10.1162/evco.1994.2.3.221 |
| [4] |
DEB K. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-2[J]. IEEE Transactuons on Evolutuinary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [5] |
ZITZLER E. Evolutionary algorithms for multiobjective optimization: Methods and applications[M]. Zurich: Doctoral Dissertation ETH 13398, Swiss Federal Institute of Technology (ETH), 1999.
|
| [6] |
ZITZLER E, LAUMANNS M, THIELE L. SPEA2: Improving the strength pareto evolutionary algorithm for multiobjective optimization[C]//Evolutionary Methods for Design, Optimization and Control with Applications to Industrial Problems. Proceedings of the EUROGEN'2001, 2001.
|
| [7] |
CORNE D W, JERRAM N R, KNOWLES J D, et al. PESA-Ⅱ: Region-based selection in evolutionary multiobjective optimization[C]// SPECTOR L, GOODMAN E D, WU A, et al. GECCO'01: Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation. San Francisco California: Morgan Kaufmann Publishers Inc., 2001: 283-290.
|
| [8] |
史晨豪, 唐忠, 戴尉阳, 等. 基于多要素改进NSGA Ⅱ算法的有源配电网多目标优化策略[J]. 供用电, 2021, 38(6): 50-55. |
| [9] |
周士鹤, 冯寅, 张克冲, 等. 基于NSGA-Ⅱ的多效蒸发海水淡化系统优化研究[J]. 热科学与技术, 2021, 20(2): 112-121. |
| [10] |
SVLFLOW A, DRECHSLER N, DRECHSLER R. Robust multi-objective optimization in high dimensional spaces[C]//OBAYASHI S, DEB K, POLONI C, et al. EMO'07: Proceedings of the 4th International Conference on Evolutionary Multi-criterion Optimization. Berlin, Heidelberg: Springer-Verlag, 2007: 715-726.
|
| [11] |
NARUKAWA K, RODEMANN T. Examining the performance of evolutionary many-objective optimization algorithms on a real-world application[C]//ICGEC'12: Proceedings of the 2012 Sixth International Conference on Genetic and Evolutionary Computing. IEEE Computer Society: Washington D C, 2012: 316-319.
|
| [12] |
王付宇, 汤涛, 李艳, 等. 疫情事件下多灾点应急资源最优化配置研究[J]. 复杂系统与复杂性科学, 2021, 18(1): 53-62. |
| [13] |
TIAN Y, WANG H, ZHANG X, et al. Effectiveness and efficiency of non-dominated sorting for evolutionary multi-and many-objective optimization[J]. Complex & Intelligent Systems, 2017, 3(4): 247-263. |
| [14] |
DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part Ⅰ: Solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535 |
| [15] |
ELARBI M, BECHIKH S, GUPTA A, et al. A new decomposition-based NSGA Ⅱ for many-objective optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 48(7): 1191-1210. DOI:10.1109/TSMC.2017.2654301 |
| [16] |
ZHANG Q, LI H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 |
| [17] |
FARIAS L, ARAÚJOL A F R. Many-objective evolutionary algorithm based on decomposition with random and adaptive weights[C]//2019 IEEE International Conference on Systems, Man and Cybernetics (SMC). IEEE, 2019: 3746-3751. DOI: 10.1109/SMC.2019.8914005.
|
| [18] |
DONG M G, LIU B, JING C. A many-objective evolutionary algorithm based on decomposition with dynamic resource allocation for irregular optimization[J]. Frontiers of Information Technology & Electronic Engineering, 2020, 21(8): 1171-1190. |
| [19] |
ZITZLER E, THIELE L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach[J]. IEEE Transactions on Evolutionary Computation, 1999, 3(4): 257-271. DOI:10.1109/4235.797969 |
| [20] |
王学武, 魏建斌, 周昕, 等. 一种基于超体积指标的多目标进化算法[J]. 华东理工大学学报: 自然科学版, 2020, 46(6): 780-791. |
| [21] |
SHANG K, ISHIBUCHI H, NI X. R2-based hypervolume contribution approximation[J]. IEEE Transactions on Evolutionary Computation, 2020, 24(1): 185-192. DOI:10.1109/TEVC.2019.2909271 |
| [22] |
谢承旺, 李凯, 廖国勇. 一种带差分局部搜索的改进型NSGA2算法[J]. 计算机科学, 2013, 40(10): 235-238, 273. |
| [23] |
XIANG Y, ZHOU Y, LI M, et al. A vector angle-based evolutionary algorithm for unconstrained many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2017, 21(1): 131-152. DOI:10.1109/TEVC.2016.2587808 |
| [24] |
LI K, FIALHOÁ, KWONG S, et al. Adaptive operator selection with bandits for a multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(1): 114-130. DOI:10.1109/TEVC.2013.2239648 |



