2. 生态环境部华南环境科学研究所, 国家环境保护城市生态环境模拟与保护重点实验室, 广东广州 510535;
3. 海南省白沙黎族自治县林业局, 海南白沙黎族自治县 572800
2. State Environmental Protection Key Laboratory of Urban Ecological Simulation and Protection, South China Institute of Environmental Science. MEE, Guangzhou, Guangdong, 510535, China;
3. Forestry Bureau of Baisha Li Autonomous County in Hainan Province, Baisha Li Autonomous County, Hainan, 572800, China
植被净初级生产力(Net Primary Productivity, NPP)是绿色植物在单位时间和单位面积上的干物质积累量[1-3],其大小不仅反映了植被的生产能力,也表征了生态系统功能和质量,在调节全球碳平衡中发挥着重要作用,成为目前研究热点之一[4-6]。传统的地面观测方法费时费力,且观测尺度有限。随着遥感技术的发展,基于遥感手段的NPP反演已比较成熟且得到广泛应用[7]。例如,巩杰等[8]采用Carnegie-Ames-Stanford Approach (CASA)模型分析甘肃白龙江流域植被NPP时空变化;刘旻霞等[9]和汪东川等[7]利用MODIS NPP产品数据,分别分析青海省和京津冀城市群植被NPP时空变化;陈晓玲等[3]分析了湖南省亚热带山地丘陵区植被NPP时空变化及其与气候因子的关系;戴尔阜等[10]研究发现中国南方红壤丘陵区植被NPP与年均温度呈负相关关系。
以往研究NPP变化趋势或NPP对气候因子的响应时,大多采用线性回归法[8, 11, 12]。这种方法对数据要求较高(如正态分布等),而自然界中的变量很难甚至不能满足上述要求,且得出的变化趋势仅为线性变化趋势,忽略了NPP变化的非线性问题。另外,以往研究在分析NPP对气候因子的响应时,忽略了气候因子间的多重共线性,从而增加了研究结果的不确定性。土地利用变化是人类活动对自然生态系统影响的最直接信号[13],直接关系到区域生态系统质量及其稳定性。如赵晓等[14]研究了土地利用变化对三峡库区重庆段植被NPP的影响,结果表明土地利用类型变化影响植被固碳能力、NPP空间分布;彭月月等[15]研究了土地利用变化对成都市植被NPP的影响,结果表明建设用地面积比例变化显著影响区域植被NPP。土地利用变化所导致的土地利用结构改变对NPP的影响,直接关系到区域碳储量变化以及区域碳中和目标的实现。土地利用变化中的城市扩张和生态恢复对NPP产生不同程度的影响,而以往研究大多只关注城市扩张对NPP的影响[16, 17],因此有必要分别探讨城市扩张和生态恢复对区域NPP的影响。
城市群作为国家经济发展的战略核心区和国家新型城镇化的主体区,在推动形成人与自然和谐发展的现代化建设新格局中发挥着重要作用。粤港澳大湾区建设是习近平总书记亲自谋划、亲自部署、亲自推进的国家重大发展战略,但随着粤港澳大湾区城市群城市化进程不断加快,该区域景观格局发生显著变化,重要生态空间和典型生态系统受到侵占与挤压,成为生态环境问题集中激化的敏感区和重点治理区。因此,本研究以粤港澳大湾区为例,探究在气候变化和人类活动干扰双重影响下,气候与土地利用变化对粤港澳大湾区植被NPP的影响,为深入研究粤港澳大湾区生态系统质量、植被保护、生态修复和区域生态安全提供科学依据。
1 材料与方法 1.1 数据来源2001-2018年Enhanced Vegetation Index (EVI)数据来源于美国国家航空航天局的地球观测系统EVI/MODIS数据集,数据空间分辨率为0.5 km,时间分辨率为16 d。气温、降雨和太阳辐射量数据来源于国家气象科学数据中心(http://data.cma.cn/),时间跨度为2001-2018年,所有数据均由国家气象科学数据中心严格检验和校正[18]。气象数据采用空间克里格插值法,输出0.5 km×0.5 km的栅格图像。土地利用类型数据来源于中国科学院资源环境科学与数据中心,空间分辨率为30 m×30 m。该数据集在全国范围内进行统一集成和质量检验,一级类型总体评价精度达到93%以上,二级类型分类综合精度达到90%以上[19]。
1.2 数据处理与分析 1.2.1 NPP反演与验证采用CASA模型对NPP进行反演,其计算过程如下:
| $ \operatorname{NPP}(x, t)=A_{\mathrm{par}}(x, t) \times \varepsilon(x, t), $ | (1) |
式中,NPP(x, t)为t时刻x像元的NPP值,Apar(x, t)和ε(x, t) 分别为t时刻x像元的光合有效辐射(MJ/m2)和实际光能利用率(gC/MJ)。
| $ A_{\mathrm{par}}(x, t)=\operatorname{Sol}_{x, t} \times F_{\mathrm{par}}(x, t) \times 0.5, $ | (2) |
| $ \begin{gathered} F_{\mathrm{par}}(x, t)= \\ {\left[\frac{\left(\mathrm{EVI}_{x, t}-\mathrm{EVI}_{i, \min }\right) \times\left(F_{\mathrm{parmax}}-F_{\mathrm{parmin}}\right)}{\left(\mathrm{EVI}_{i, \max }-\mathrm{EVI}_{i, \min }\right)+F_{\mathrm{parmin}}}+\right.} \\ \left.\frac{\left.S_{r}(x, t)-S_{r i, \min }\right) \times\left(F_{\mathrm{parmax}}-F_{\mathrm{parmin}}\right)}{\left(S_{r i, \max }-S_{r i, \min }\right)+F_{\mathrm{parmin}}}\right] / 2, \end{gathered} $ | (3) |
| $ S_{r}(x, t)=\frac{1+\mathrm{EVI}_{x, t}}{1-\mathrm{EVI}_{x, t}}, $ | (4) |
式中,Solx, t为t时刻x像元的太阳总辐射量(MJ/m2);Fpar(x, t)为t时刻x像元的光合有效辐射吸收比例;Fparmax和Fparmin分别取值0.95和0.001;EVIi, max和EVIi, min分别为i类型EVI的最大值和最小值,分别取位于EVI的95%和5%位置的值;Sri, max和Sri, min分别为i类型Sr的最大值和最小值。
| $ \varepsilon(x, t)=T_{1}(x, t) \times T_{2}(x, t) \times W_{\varepsilon}(x, t) \times \varepsilon_{\max }, $ | (5) |
式中,εmax为最大光能利用率(gC/MJ);T1(x, t)、T2(x, t)和Wε(x, t)分别表示t时刻x像元的最大光能利用率在最低温、最高温和水分缺乏时的胁迫系数:
| $ T_{1}(x, t)=0.8+0.02 \times T_{\mathrm{opt}}^{x}+0.0005 \times T_{\mathrm{opt}}^{x}{}^2, $ | (6) |
| $ \begin{gathered} T_{2}(x, t)= \\ \frac{1.184}{\left\{1+e^{0.2 \times\left(T_{\mathrm{opt}}^{x}-10-T(x, t)\right)}\right\} \times\left\{1+e^{0.3 \times\left(-T_{\mathrm{opt}}^{x}-10+T(x, t)\right)}\right\}}, \end{gathered} $ | (7) |
| $ W_{\varepsilon}(x, t)=\frac{\operatorname{EET}(x, t)}{\operatorname{PET}(x, t)} \times 0.5+0.5, $ | (8) |
式中,Toptx为植被生长的最适温度(℃),取一年中最大EVI所在月份的平均温度(℃);T(x, t)为x像元在t时刻的平均温度;EET(x, t)为x像元在t时刻的实际蒸散量(mm),PET(x, t)为x像元在t时刻的潜在蒸散量(mm)。
当T(x, t)≤10℃时,T1(x, t)=0;当T(x, t)>Toptx+10℃或者T(x, t) < Toptx-13℃时,该月植被最大光能利用率在最高温时的温度胁迫系数为T(x, t)达到最适温度(Toptx)时T2(x, t)值的一半。
由于NPP一般很难直接观测,因此参照以往研究[20],将获取的区县森林资源清查资料依据公式(9)转为NPP,并与CASA模型反演结果进行比较。
| $ \mathrm{NPP}=\text { Biom } \times 0.475 $ | (9) |
式中,Biom为森林资源清查资料获取的生物量。
1.2.2 时间变化趋势分析采用Mann-Kendall统计检验法和非参数Sen分析法分析2001-2018年NPP变化趋势,其计算方法如下所述。
Mann-Kendall的统计量S为
| $ S=\sum\nolimits_{i=1}^{n-1} \sum\nolimits_{j=i+1}^{n} \operatorname{sgn}\left(x_{j}-x_{i}\right),$ | (10) |
式中n为观测次数,xi和xj分别为在时间序列i和j上对应的NPP值(j>i),sgn(xj-xi)为符号函数,其计算公式为
| $ \operatorname{sgn}\left(x_{j}-x_{i}\right)=\left\{\begin{array}{l} +1, x_{j}-x_{i}>0 \\ 0, \quad x_{j}-x_{i}=0 \\ -1, x_{j}-x_{i}<0 \end{array}\right.,$ | (11) |
其方差计算公式为
| $ \begin{array}{l} \ \ \ \ \operatorname{Var}(S)= \\ \frac{n(n-1)(2 n-1)-\sum\nolimits_{i=1}^{m} t_{i}\left(t_{i}-1\right)\left(2 t_{i}+5\right)}{18}, \end{array} $ | (12) |
式中,n为观测次数,m为序列中秩次相同的组数,ti为第i组秩次相同所包含观测值的个数。
Neeti等[21]研究表明,当n>8时,标准化检验统计量ZS符合标准正态分布,其计算公式为
| $ Z_{s}=\left\{\begin{array}{l} \frac{S-1}{\sqrt{\operatorname{Var}(s)}}, &S>0 \\ 0, & S=0 \\ \frac{S+1}{\sqrt{\operatorname{Var}(s)}}, &S<0 \end{array}\right.。$ | (13) |
当Zs>0时表示变化趋势为上升趋势,当Zs < 0时表示变化趋势为下降趋势。Mann-Kendall趋势分析法强调的是单调趋势,并不一定为线性趋势,而且该方法只是反映趋势的变化,并不体现变化的幅度,因此引入Sen's斜率法对变化幅度进行计算,其计算公式Qi为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ Q_{i}=\operatorname{medium}\left(\frac{x_{j}-x_{i}}{j-i}\right), i=1,2, \cdots, n-1 \\ (j>i)。\end{array} $ | (14) |
为进一步分析NPP未来变化趋势,本研究采用基于R/S的Hurst指数进行分析。其基本计算过程如下: 设在t1, t2, …, tn时刻所对应的NPP分别为NPP1, NPP2, …, NPPn,对任意正整数m,该时刻的平均值NPPm为
| $ \overline{\mathrm{NPP}_{m}}=\frac{1}{m} \times \sum\nolimits_{t=1}^{m} \mathrm{NPP}_{t}, t=1,2, \cdots, n, $ | (15) |
其累积离差Xt可表示为
| $ X_{t}=\sum\limits_{t=1}^{t}\left(\mathrm{NPP}_{t}-\overline{\mathrm{NPP}_{m}}\right), 1 \leqslant t \leqslant m。$ | (16) |
把同一个m值所对应的最大Xt和最小Xt之间差记为极差Rm,则
| $ R_{m}=\max \limits_{1 \leqslant t \leqslant m} X_{t}-\min \limits_{1 \leqslant t \leqslant m} X_{t}, t=1,2, \cdots, n, $ | (17) |
其标准差记为Sm,则
| $ \begin{array}{l} \ \ \ \ \ \ \ \ S_{m}=\left[\frac{1}{m} \times \sum\nolimits_{t=1}^{m}\left(\mathrm{NPP}_{t}-\overline{\mathrm{NPP}_{m}}\right)^{2}\right]^{1 / 2}, t=1 ,\\ 2, \cdots, n。\end{array} $ | (18) |
由此,
H取值范围为0-1。当H>0.5时,表示NPP未来变化趋势与过去一致,H值越接近1,说明持续性越强。相反,当H < 0.5时,表示NPP未来变化趋势与过去相反,H值越接近0,表示反持续性越强。当H=0.5时,表示各项指标完全独立,过程是随机性的。
1.2.4 相关关系与响应分析为分析粤港澳大湾区植被NPP与气候变化之间的关系,本研究选择生长季平均气温和累积降雨两个气候因子,分析NPP与气候变化的相关性,其计算公式为
| $ R_{i j \cdot k}=\frac{R_{i j}-R_{i k} \times R_{j k}}{\sqrt{\left(1-R_{i k}^{2}\right)} \times \sqrt{\left(1-R_{j k}^{2}\right)}}, $ | (19) |
式中Rij·k为控制变量k的情况下,变量i和j的偏相关系数;Rij, Rik, Rjk分别为变量i和j,变量i和k,变量j和k的简单相关系数。
为减小气候因子对NPP影响的多重共线性,本研究采用偏最小二乘回归法分析NPP对平均气温和累积降雨的响应。该方法集多元线性回归、典型相关性分析和主成分分析于一体,能够在自变量存在多重相关性的条件下进行回归建模。
1.2.5 土地利用变化对NPP影响根据2000年和2018年土地利用类型中的一级分类,以土地利用类型——森林、灌丛、草地、农田、城镇和未利用地为研究对象。其中2000年土地利用类型为森林、灌丛、草地的像元,至2018年转变为城镇的,本研究定义为城市扩张;2000年为农田和未利用地的像元,至2018年转变为森林、草地和灌丛的,本研究定义为生态恢复。由于在2000-2018年,粤港澳大湾区城镇建设用地一般不会转变为森林、草地和灌丛用地,因此本研究不考虑城镇建设用地转变为森林、草地和灌丛的情形。统计NPP像元(0.25 km2)中土地利用类型发生转变的像元个数,并计算其占比。最后,耦合NPP变化趋势,分析土地利用变化对植被NPP的影响。
2 结果与分析 2.1 NPP验证由验证结果可知(图 1),CASA模型反演的粤港澳大湾区NPP结果与实际结果较为吻合,其R2为0.68 (P < 0.05),RMSE为0.16 kg·C·m-2。
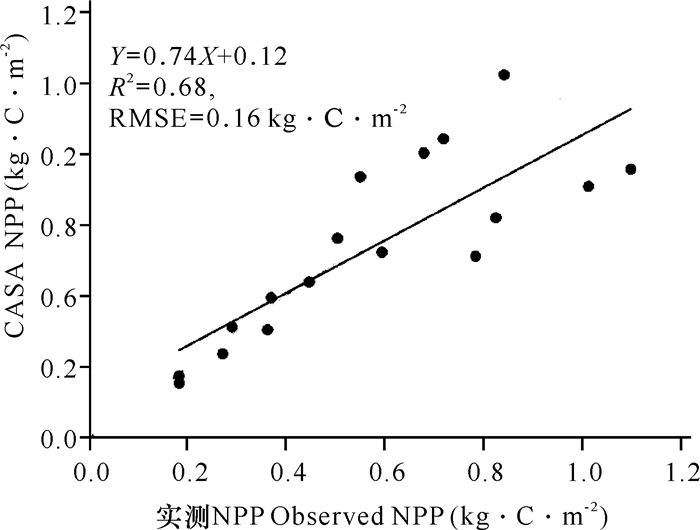
|
| 图 1 NPP验证 Fig. 1 Validation of NPP |
2.2 NPP空间分布特征
从图 2a可以看出,2001-2018年粤港澳大湾区NPP年均值为0.08-1.51 kg·C·m-2,平均值为0.89 kg·C·m-2。NPP最低值主要分布在中心区,其值一般低于0.4 kg·C·m-2;NPP最高值主要分布在粤港澳大湾区西北部、东北部和东部部分区域,其值一般在1.0 kg·C·m-2以上;其他区域如粤港澳大湾区西南部和东南部,NPP值一般为0.4-1.0 kg·C·m-2。由NPP标准差空间分布(图 2b)可知,NPP标准差较低值主要分布在粤港澳大湾区中部,其值一般在0.04 kg·C·m-2以下;粤港澳大湾区西南部和东南部,NPP标准差较大,一般在0.1 kg·C·m-2以上;其他区域,如粤港澳大湾区东北部和西北部,NPP标准差一般为0.06-0.1 kg·C·m-2。可见粤港澳大湾区中部NPP年际变化较小,而粤港澳大湾区西南部和东南部NPP年际变化较大。
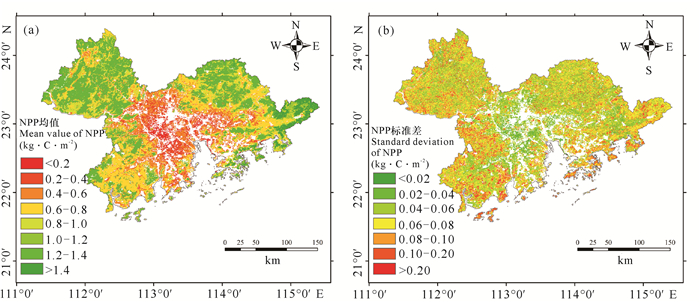
|
| 图 2 粤港澳大湾区NPP(a)及其标准差(b)空间分布 Fig. 2 Spatial distribution of NPP (a) and its standard deviation (b) in Guangdong-Hong Kong-Macao Greater Bay Area |
2.3 NPP时间变化趋势
由NPP时间变化趋势(图 3a)看,2001-2018年粤港澳大湾区NPP总体呈现增加趋势,其速率约为0.001 kg·C·m-2·a-1。NPP增加区域约占总面积的58.42%,主要分布在粤港澳大湾区中部和西南部。增长速率较高的区域主要分布在粤港澳大湾区西南部,其增长速率一般在0.005 kg·C·m-2·a-1以上。NPP呈负增长区域主要分布在粤港澳大湾区西北部、东北部和东南部部分区域,约占研究区面积的41.58%,其速率一般为-0.02-0 kg·C·m-2·a-1。从NPP变化趋势显著性来看(图 3b),约30.40%的区域表现为NPP呈显著增加(P < 0.05)或极显著增加(P < 0.01)趋势,主要分布在粤港澳大湾区西南部和西部。NPP呈显著降低(P < 0.05)或极显著降低(P < 0.01)区域较小,约占总面积的13.80%,且集中分布在粤港澳大湾区东南部和南部。
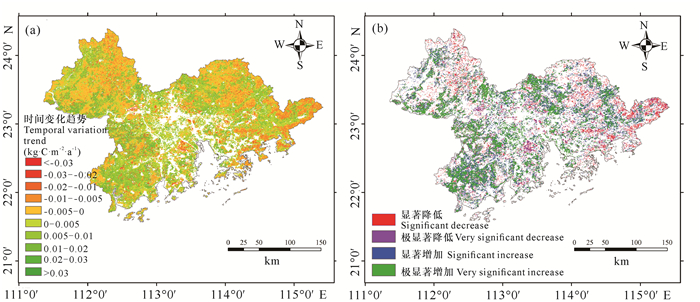
|
| 图 3 2001-2018年NPP时间变化趋势 Fig. 3 Temporal variation trend of NPP between 2000 and 2018 |
由Hurst指数可以看出,粤港澳大湾区NPP的Hurst指数主要在0.5以下,约占研究区面积的66.52%,而Hurst指数为0.5-1的约占研究区的33.48%(图 4a)。由此可见,粤港澳大湾区大部分区域的NPP未来变化趋势与目前相反。通过耦合NPP时间变化趋势和Hurst指数发现,未来粤港澳大湾区约有66.52%的区域NPP呈现下降趋势(图 4b),其中28.01%的区域表现为持续下降趋势,主要分布在研究区东部和西北部;38.51%的区域表现为NPP由上升转变为下降趋势,主要分布在粤港澳大湾区的中部和西南部。32.58%的区域NPP未来呈上升趋势,其中19.01%的区域表现为持续上升趋势,主要零散分布于粤港澳大湾区中部和东部;13.57%的区域表现为NPP由原来的下降趋势转变为未来的上升趋势。
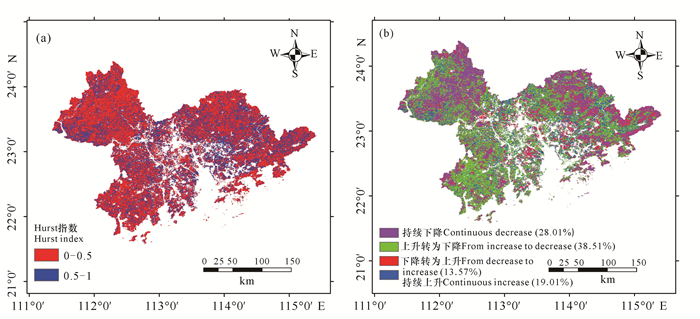
|
| 图 4 粤港澳大湾区植被NPP未来变化趋势 Fig. 4 Future variation trend of NPP in Guangdong-Hong Kong-Macao Greater Bay Area |
2.4 NPP与平均气温、累积降雨变化关系 2.4.1 NPP与平均气温、累积降雨变化相关关系
粤港澳大湾区植被NPP与生长季平均气温之间的偏相关系数平均值为0.18,且偏相关系数主要为-0.3-0.3。NPP与平均气温呈正相关区域约占整个研究区的54.34%(图 5a),但只有1.25%的区域表现为显著正相关关系(P < 0.05),NPP与平均气温呈正相关关系主要分布在粤港澳大湾区西南部。NPP与平均气温呈负相关关系约占整个区域的45.66%,主要分布在研究区的北部、西北部和东北部(图 5c)。
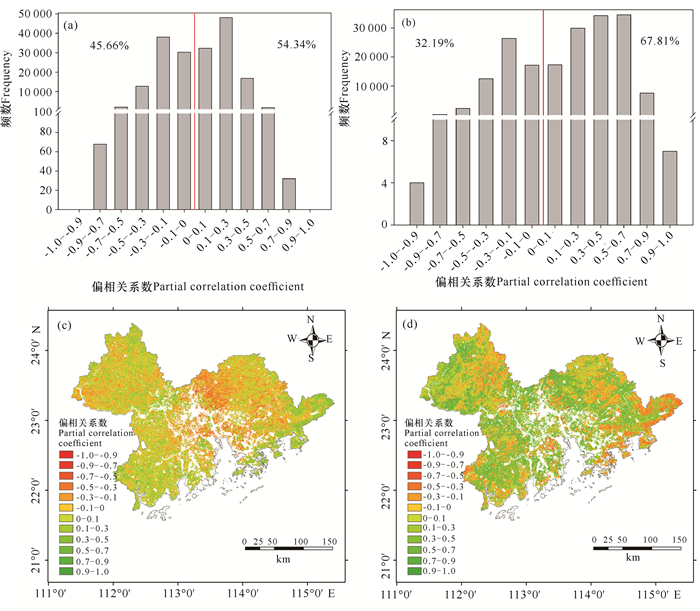
|
| 图 5 NPP与平均气温(a, c)和累积降雨(b, d)的偏相关关系及其空间分布 Fig. 5 Frequency distribution of partial correlations between NPP and mean temperature (a, c) and cumulative precipitation (b, d), and its corresponding spatial distribution |
从NPP与生长季累积降雨看,NPP与累积降雨偏相关系数平均值为0.32,高于NPP与平均气温之间的偏相关系数,且主要表现为正相关关系,占研究区总面积的67.81%(图 5b),其中25.03%的区域表现出显著正相关关系(P < 0.05),NPP与累积降雨呈正相关关系区域主要集中在研究区中部和西南部。NPP与累积降雨呈负相关关系区域约占总面积的32.19%,其中仅1.70%的区域表现为显著负相关关系(P < 0.05),而NPP与累积降雨呈负相关关系区域主要分布在东部和西北部(图 5d)。
2.4.2 NPP对平均气温、累积降雨变化的响应从NPP对平均气温变化的响应空间分布看(图 6a),NPP对平均气温变化表现为正响应的区域主要位于研究区西南部和东南部,而负响应关系主要位于研究区西北部、东北部和北部。从NPP对平均气温变化的响应值来看,54.34%的区域表现为NPP对平均气温变化呈正响应,其均值为0.007 kg·C·m-2·a-1·℃-1。从NPP对平均气温变化响应值频数分布看,NPP对平均气温变化的正响应值主要集中在0-0.03 kg·C·m-2·a-1·℃-1;类似地,负响应值主要集中在-0.03-0 kg·C·m-2·a-1·℃-1(图 6c)。
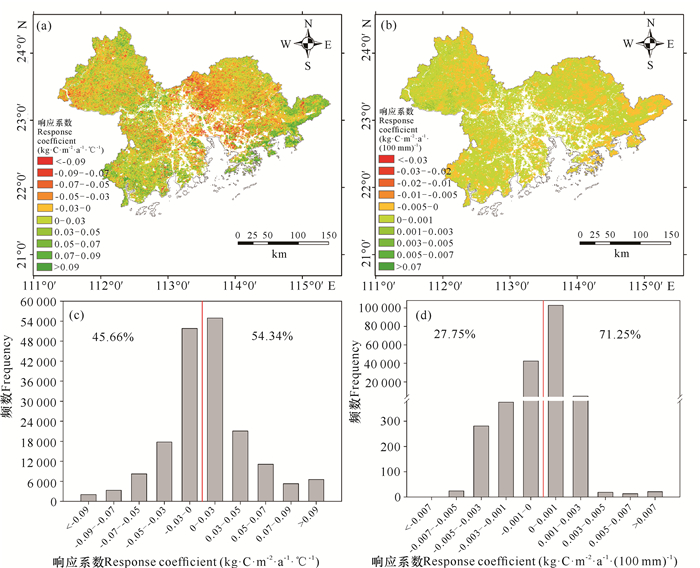
|
| 图 6 NPP对生长季平均气温(a, c)和累积降雨(b, d)的响应空间分布及其响应系数频数分布 Fig. 6 Spatial distribution of sensitivity of NPP to mean temperature (a, c) and cumulative precipitation (b, d) and its corresponding frequency in the growing season |
从NPP对累积降雨变化响应的空间分布看(图 6b),NPP对累积降雨变化的正响应关系主要分布在研究区中部、西南部和西北部,负响应关系主要分布在研究区东部和北部。从NPP对累积降雨变化的响应值看,NPP对累积降雨变化的响应主要表现为正响应,约占研究区总面积的71%,响应均值为0.000 1 kg·C·m-2·a-1·(100 mm)-1。从响应值的频数分布看,NPP对累积降雨变化的正响应值主要集中在0-0.001 kg·C·m-2·a-1·(100 mm)-1,其次为0.001-0.003 kg·C·m-2·a-1·(100 mm)-1,NPP对累积降雨变化的负响应值频数分布也表现出类似的规律(图 6d)。
2.5 土地利用变化对NPP影响从土地利用变化对NPP影响可以看出(图 7),城市扩张对NPP表现为显著的负效应(P < 0.000 1),随着建成区面积比例的增加,NPP年际变化率为-5.68×10-5 kg·C·m-2·a-1。而生态恢复对NPP存在显著的正效应(P < 0.000 1),生态恢复面积每增加1个百分比,NPP年际变化率增加约为5.81×10-6 kg·C·m-2·a-1。可见,城市扩张对NPP年际变化率的影响远高于生态恢复。
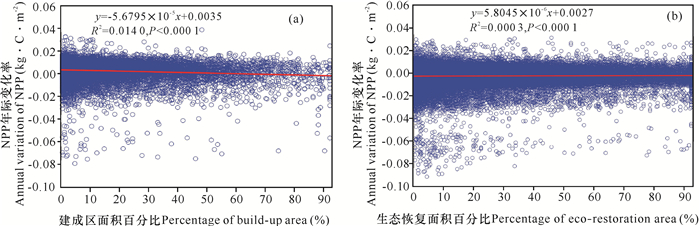
|
| 图 7 土地利用变化对NPP影响 Fig. 7 Effects of land use variation on NPP |
3 讨论 3.1 NPP时空格局演变
在气候变化与碳中和目标背景下,植被NPP动态变化及其与气候变化的关系受到高度关注。目前NPP计算原理和方法较为成熟,多为基于遥感数据的模拟计算[8],但受到遥感传感器及气候数据插值结果影响,反演结果也存在差异。本研究表明2001-2018年粤港澳大湾区NPP年均值为0.08-1.51 kg·C·m-2,平均值为0.89 kg·C·m-2。吴艳艳[22]研究结果表明广州市2001-2013年NPP平均值为0.66-0.85 kg·C·m-2,本研究结果与其相比略偏高,主要是因为本研究区为粤港澳大湾区,除广州市外,位于粤港澳大湾区的肇庆、惠州等地市的林地覆盖面积广,植被覆盖度较高,所以造成NPP较高。
从NPP空间分布看,NPP均值总体呈现中部和南部低,西北部和东北部高的空间分布特征。这主要是因为粤港澳大湾区中部和南部城市化程度高,人为活动干扰强,城市化发展使城市周围自然生态系统减少、质量下降,植被覆盖度变低[8];而大湾区西北部和东北部,植被类型主要以林地为主,植被覆盖度高,生态系统结构复杂,稳定性相对较高[7],这与前人研究结果一致[7, 22, 23]。
从NPP变化趋势看,NPP总体呈增加趋势。这可能是由于随着我国生态文明建设,粤港澳大湾区各地市加快生态文明建设,生态系统质量不断提高,同时城市化过程对自然生态系统干扰已引起重视,人类活动对自然生态系统干扰程度逐渐降低。此外,森林分类经营、天然林保护和人工林面积增加[24]等措施的实施也是大湾区NPP增加的另一重要原因。
从NPP未来变化趋势看,粤港澳大湾区NPP总体呈下降趋势,约占研究区总面积的66.52%,这可能与未来城市的进一步建设扩张有关[25],本研究中城市扩张对NPP的负效应也证明了此结论。由NPP未来变化趋势可知,粤港澳大湾区生态环境质量在未来有下降趋势,特别是对于粤港澳大湾区东南部、南部和西北部而言,应加强践行“绿水青山就是金山银山”理念和生态保护措施,严格落实生态保护红线,增强生态环境分区管控力度,提升生态环境质量,对生态系统遭到破坏(如乱砍乱伐)的区域,应因地制宜实施生态修复,从而提升区域生态安全和质量。
3.2 NPP与气候因子的关系平均气温和累积降雨是影响NPP变化的两个重要气候因子[26]。根据IPCC第五次研究报告,气候变化与碳循环存在显著的正相关关系,但这种关系随区域变化而变化。本研究表明,NPP与生长季平均气温和累积降雨总体呈正相关关系,其偏相关系数分别为0.18和0.32,响应均值分别为0.007 kg·C·m-2·a-1·℃-1和0.000 1 kg·C·m-2·a-1·(100 mm)-1。以往研究表明气温、降雨与研究区植被NPP密切相关,且NPP与降雨关系更为密切[9, 12, 27]。这可能是因为温度上升使得植被蒸腾作用增强,土壤水分减少,温度对植被生理活动的限制也随之增强,从而阻碍植被生长及其光合作用[28]; 而充足的降雨不仅可以满足植被生长需要,也可以缓解因高温导致的强蒸散发对植被生长的影响。
3.3 土地利用变化对NPP的影响快速城市化地区的土地利用变化,必然导致植被类型、结构和区域配置状况显著改变[29],而人为活动下的土地利用变化是影响植被NPP变化的重要因素[30],其影响主要来源于土地利用变化过程及其用地功能转变。本研究结果表明, 城市扩张对植被NPP产生极显著的负效应,而生态恢复则对NPP产生极显著正效应,这与前人研究结论一致[14, 15]。城市扩张使得区域内土地功能发生转变,景观破碎化和异质性增强[14],生态系统结构变化和功能降低,从而导致植被NPP下降;而生态工程建设(如退耕还林、植树造林)不仅增加了植被覆盖面积,在人为干预下(如施肥、集约化管理),植被生长环境得以改善,从而有利于植被NPP的积累。此外,本研究表明,城市扩张对NPP影响高于生态恢复对NPP的影响。因此,粤港澳大湾区在关注生态恢复对植被NPP和生态环境质量影响的同时,更应关注城市扩张对植被生长的负面影响。值得注意的是,虽然城市扩张和生态恢复均对NPP产生极显著影响,但NPP变化受多重影响因子以及影响因子间交互作用的共同影响,致使本研究模型所得R2较小。因此,关于城市扩张和生态恢复对NPP的影响有待于进一步探讨。
4 结论本研究利用CASA模型反演2001-2018年粤港澳大湾区NPP,分析NPP时空格局演变及其与气候、土地利用变化的关系。研究结论如下:
① 从NPP时空格局演变看,粤港澳大湾区NPP均值呈中心区和东南区向东北、西北方向递增的趋势,2001-2018年NPP总体呈增加趋势。
② NPP与平均气温和累积降雨总体呈正相关关系,但NPP与累积降雨的相关性大于NPP与平均气温的相关性。
③ 城市扩张和生态恢复对NPP均产生极显著影响,但城市扩张对NPP产生的负效应远高于生态恢复对NPP产生的正效应。
| [1] |
FIELD C B, RANDERSON J T, MALMSTRÖM C M. Global net primary production: Combining ecology and remote sensing[J]. Remote Sensing of Environment, 1995, 51(1): 74-88. DOI:10.1016/0034-4257(94)00066-V |
| [2] |
LI J, CUI Y P, LIU J Y, et al. Estimation and analysis of net primary productivity by integrating MODIS remote sensing data with a light use efficiency model[J]. Ecological Modelling, 2013, 252: 3-10. DOI:10.1016/j.ecolmodel.2012.11.026 |
| [3] |
陈晓玲, 曾永年. 亚热带山地丘陵区植被NPP时空变化及其与气候因子的关系——以湖南省为例[J]. 地理学报, 2016, 71(1): 35-48. |
| [4] |
GAO Y H, ZHOU X, WANG Q, et al. Vegetation net primary productivity and its response to climate change during 2001-2008 in the Tibetan Plateau[J]. Science of the Total Environment, 2013, 444: 356-362. DOI:10.1016/j.scitotenv.2012.12.014 |
| [5] |
ZHANG M L, LAL R, ZHAO Y Y, et al. Spatial and temporal variability in the net primary production of grassland in China and its relation to climate factors[J]. Plant Ecology, 2017, 218(9): 1117-1133. DOI:10.1007/s11258-017-0756-4 |
| [6] |
MAO D H, LUO L, WANG Z M, et al. Variations in net primary productivity and its relationships with warming climate in the permafrost zone of the Tibetan Plateau[J]. Journal of Geographical Sciences, 2015, 25(8): 967-977. DOI:10.1007/s11442-015-1213-8 |
| [7] |
汪东川, 曹泽军, 张利辉, 等. 京津冀城市群NPP时空分布及其影响因素研究[J]. 环境生态学, 2020, 2(5): 1-10. |
| [8] |
巩杰, 曹二佳, 李红瑛, 等. 2000-2013年甘肃白龙江流域植被NPP时空变化及其影响因素[J]. 兰州大学学报: 自然科学版, 2020, 56(2): 154-161, 168. |
| [9] |
刘旻霞, 焦骄, 潘竟虎, 等. 青海省植被净初级生产力(NPP)时空格局变化及其驱动因素[J]. 生态学报, 2020, 40(15): 5306-5317. |
| [10] |
戴尔阜, 李双元, 吴卓, 等. 中国南方红壤丘陵区植被净初级生产力空间分布及其与气候因子的关系——以江西省泰和县为例[J]. 地理研究, 2015, 34(7): 1222-1234. |
| [11] |
王馨爽, 吴梦月, 马红利, 等. 渭河流域长时间序列NPP估算及时空变化特征分析[J]. 西北林学院学报, 2020, 35(6): 205-211. DOI:10.3969/j.issn.1001-7461.2020.06.28 |
| [12] |
高艺宁, 王宏亮, 赵萌莉. 内蒙古荒漠草原植被NPP时空变化及气候因子分析: 以四子王旗为例[J]. 中国农业大学学报, 2020, 25(8): 100-107. |
| [13] |
姜雨青, 李宝富, 宋美帅, 等. 定量评估我国西北干旱区土地利用变化对植被指数的影响[J]. 冰川冻土, 2018, 40(3): 616-624. |
| [14] |
赵晓, 周文佐, 田罗, 等. 土地利用变化对三峡库区重庆段植被净初级生产力的影响[J]. 生态学报, 2018, 38(21): 7658-7668. |
| [15] |
彭月月, 魏妍冰, 李启权, 等. 气候和土地利用变化对成都市植被NPP时空分布的影响[J]. 西南大学学报: 自然科学版, 2018, 40(11): 150-159. |
| [16] |
张荞, 陈慧, 王萍, 等. 基于多源遥感影像的城市化及其生态效应研究[J]. 地理空间信息, 2018, 16(7): 58-62. DOI:10.3969/j.issn.1672-4623.2018.07.018 |
| [17] |
李建国, 王欢, 王净, 等. 基于线性拟合的城市化过程对陆地生态系统生产能力的影响——以江苏省为例[J]. 资源科学, 2018, 40(1): 32-43. |
| [18] |
XU L, CHEN X Q. Regional unified model-based leaf unfolding prediction from 1960 to 2009 across northern China[J]. Global Change Biology, 2013, 19(4): 1275-1284. DOI:10.1111/gcb.12095 |
| [19] |
刘纪远, 宁佳, 匡文慧, 等. 2010-2015年中国土地利用变化的时空格局与新特征[J]. 地理学报, 2018, 73(5): 789-802. |
| [20] |
LUO Z H, WU W C, YU X J, et al. Variation of net primary production and its correlation with climate change and anthropogenic activities over the Tibetan Plateau[J]. Remote Sensing, 2018, 10(9): 1352. DOI:10.3390/rs10091352 |
| [21] |
NEETI N, EASTMAN J R. A contextual Mann-Kendall approach for the assessment of trend significance in image time series[J]. Transactions in GIS, 2011, 15(5): 599-611. DOI:10.1111/j.1467-9671.2011.01280.x |
| [22] |
吴艳艳. 城市化过程广州土地覆盖变化对净初级生产力格局的影响[D]. 广州: 中山大学, 2016.
|
| [23] |
袁甲, 沈非, 聂兵, 等. 皖江城市带植被NPP时空变化及其气候响应[J]. 测绘科学, 2017, 42(11): 62-67. |
| [24] |
杨加志, 张红爱, 严玉莲, 等. 基于森林资源连续清查的广东省人工林资源动态分析[J]. 林业与环境科学, 2019, 35(2): 95-99. |
| [25] |
胡顺石, 彭雨龙, 秦建新, 等. 长株潭城市群植被指数动态变化及城市扩展对其影响分析[J]. 经济地理, 2019, 39(12): 178-186. |
| [26] |
周杰, 张昌盛, 解修平. 渭河流域植被净初级生产力时空格局及影响因素分析[J]. 水土保持学报, 2015, 29(2): 274-277. |
| [27] |
李刚, 周磊, 王道龙, 等. 内蒙古草地NPP变化及其对气候的响应[J]. 生态环境, 2008, 17(5): 1948-1955. |
| [28] |
PIAO S L, YIN G, TAN J, et al. Detection and attribution of vegetation greening trend in China over the last 30 years[J]. Global Change Biology, 2015, 21(4): 1601-1609. |
| [29] |
SENAY G B, ELLIOTT R L. Combining AVHRR-NDVI and landuse data to describe temporal and spatial dynamics of vegetation[J]. Forest Ecology and Management, 2000, 128(1/2): 83-91. |
| [30] |
TASSER E, TAPPEINER U. Impact of land use changes on mountain vegetation[J]. Applied Vegetation Science, 2002, 5(2): 173-184. |



