煮糖结晶是糖分从液相到固相转变的关键环节,利用蒸汽在结晶罐内对糖膏进行加热,并通过抽真空降低沸点、控制入料量等操作保持入料与水分蒸发平衡,使糖液过饱和度处于亚稳定区,进而析出糖晶体。煮糖过程具有多参数、强耦合、非线性、大时滞的特点,难以建立精确的机理模型用于实现自动控制。传统的控制方式依靠工人从结晶罐中抽取糖膏样品,根据经验判断结晶状态后调节阀门开度,不仅工作强度大且容易造成煮糖时间过长等问题。研究煮糖过程的自动控制方法,对解放劳动力和提高生产效率具有重要意义。
目前,针对煮糖的自动控制方法可分为反馈控制与预测控制两类。反馈控制根据系统当前输出与目标的偏差确定下一步操作,基于模糊PID、线性化和经验知识的反馈控制策略被用于控制煮糖过程[1-3]。反馈控制具有滞后性,面对复杂多变的煮糖过程,当出现不良结晶状态时,只能被动适应进行调节。预测控制基于预测模型预测系统的未来输出,并优化系统输入以使未来输出符合预期目标[4, 5]。由于具有预见性,预测控制可以减少或避免不良状况的发生,适合具有大时滞的煮糖过程。前人提出了以电导率[6]、过饱和度[7, 8]、晶体含量[9, 10]和入料流量[11]等作为控制对象的煮糖预测控制方法,但电导率在煮糖过程中呈现非单调变化,过饱和度与晶体含量目前无法准确在线测量,这导致所提出的部分方法难以在生产中应用。煮糖工艺常采用连续入料、逐步浓缩上升法,该工艺将煮糖过程分为若干个阶段,设定每个阶段糖膏液位和锤度的增加量,通过调节阀门控制糖膏液位和锤度的变化,直到最后一个阶段达到设定的卸糖液位和锤度。因此可通过自动控制液位和锤度的变化来实现自动煮糖。本研究基于核极限学习机(Kernel Extreme Learning Machine,KLEM)建立糖膏液位和锤度的预测模型,并利用粒子群优化(Particle Swarm Optimization,PSO)算法在线优化阀门开度对理想煮糖工艺曲线进行跟踪,进而实现煮糖结晶自适应控制。
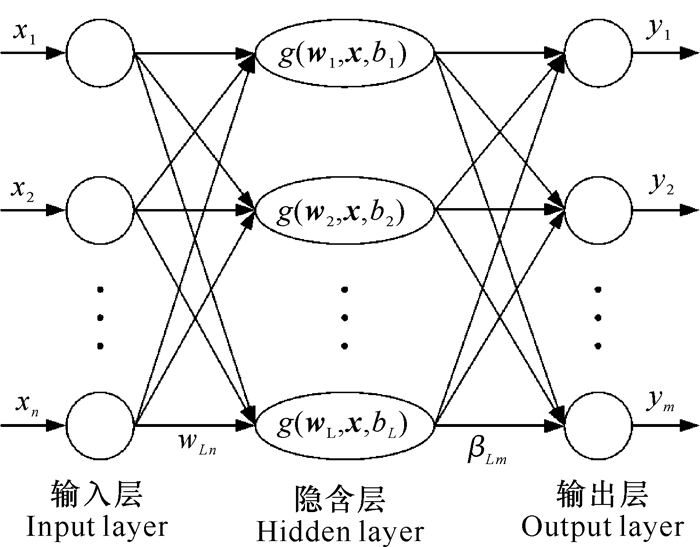
1 基于KELM的煮糖结晶预测模型 1.1 KELM极限学习机(Extreme Learning Machine,ELM)是一种单隐含层前馈神经网络,其输入层权值和隐含层偏置随机设定,输出层权值基于最小二乘法直接计算,整个过程一次完成,无需迭代,具有快速学习的能力[12, 13]。一个具有L个隐含层神经元的极限学习机网络结构如图 1所示。
|
| 图 1 极限学习机网络结构 Fig. 1 Network of extreme learning machine |
用包含N个样本的样本集S= {(xk, yk)} k=1N对上述网络进行训练,其中,xk= (xk1, xk2, …, xkn) T∈ R n是输入矩阵,表示有n个输入变量;yk= (yk1, yk2, …, ykm) T∈ R m是输出矩阵,表示有m个输出变量。根据前馈神经网络结构原理,输入与输出的函数关系可用式(1)表示。
| $ \sum\limits_{i=1}^{L} \boldsymbol{\beta}_{i} g\left(\boldsymbol{w}_{i} \cdot \boldsymbol{x}_{k}+b_{i}\right)=\boldsymbol{y}_{k},(k=1,2, \cdots, N), $ | (1) |
式中: g(·)为隐含层神经元的激活函数,w i为网络输入权值,bi为隐含层神经元的偏置,β i为网络输出权值。将式(1)写成由N个方程组成的矩阵形式,可表示为
| $ \boldsymbol{H} \boldsymbol{\beta}=\boldsymbol{Y}, $ | (2) |
式中: H为隐含层输出矩阵,β为输出权值矩阵,Y为期望输出矩阵。
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \boldsymbol{H}=\boldsymbol{H}\left(\boldsymbol{w}_{1}, \boldsymbol{w}_{2}, \cdots, \boldsymbol{w}_{L}, b_{1}, b_{2}, \cdots, b_{L}, \boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \cdots,\right. \\ \left.\boldsymbol{x}_{N}\right)= \\ \left(\begin{array}{cccc} g\left(\boldsymbol{w}_{1} \cdot \boldsymbol{x}_{1}+b_{1}\right) & g\left(\boldsymbol{w}_{2} \cdot \boldsymbol{x}_{1}+b_{2}\right) & \cdots & g\left(\boldsymbol{w}_{L} \cdot \boldsymbol{x}_{1}+b_{L}\right) \\ g\left(\boldsymbol{w}_{1} \cdot \boldsymbol{x}_{2}+b_{1}\right) & g\left(\boldsymbol{w}_{2} \cdot \boldsymbol{x}_{2}+b_{2}\right) & \cdots & g\left(\boldsymbol{w}_{L} \cdot \boldsymbol{x}_{2}+b_{L}\right) \\ \vdots & \vdots & \ddots & \vdots \\ g\left(\boldsymbol{w}_{1} \cdot \boldsymbol{x}_{N}+b_{1}\right) & g\left(\boldsymbol{w}_{2} \cdot \boldsymbol{x}_{{N}}+b_{2}\right) & \cdots & g\left(\boldsymbol{w}_{L} \cdot \boldsymbol{x}_{N}+b_{L}\right) \end{array}\right)_{N \times L}, \end{array} $ | (3) |
| $ \boldsymbol{\beta}=\left(\begin{array}{c} \boldsymbol{\beta}_{1}^{\mathrm{T}} \\ \boldsymbol{\beta}_{2}^{\mathrm{T}} \\ \vdots \\ \boldsymbol{\beta}_{L}^{\mathrm{T}} \end{array}\right)_{L \times m}, \boldsymbol{Y}=\left(\begin{array}{c} \boldsymbol{y}_{1}^{\mathrm{T}} \\ \boldsymbol{y}_{2}^{\mathrm{T}} \\ \vdots \\ \boldsymbol{y}_{N}^{\mathrm{T}} \end{array}\right)_{N \times m}。$ | (4) |
输出权值矩阵β通过最小二乘法求解式(2)获得
| $ {\mathop {\boldsymbol{\beta}}\limits^ \wedge }=\boldsymbol{H}^{\mathit{\dagger}} \boldsymbol{Y}, $ | (5) |
式中: H†是隐含层输出矩阵H的Moore-Penrose广义逆矩阵。ELM基于经验风险最小化原理进行学习,容易出现过拟合现象,为提高其泛化能力,在式(5)中引入正则化参数C,则输出权值矩阵由式(6)求解[14]。
| $ {\mathop {\boldsymbol{\beta}}\limits^ \wedge }=\boldsymbol{H}^{\mathrm{T}}\left(\frac{\boldsymbol{I}}{C}+\boldsymbol{H} \boldsymbol{H}^{\mathrm{T}}\right)^{-1} \boldsymbol{Y}, $ | (6) |
式中: I为N维单位矩阵。由于核映射比随机映射具有更好的泛化能力和稳定性,Huang等[15]将核函数引入ELM进而发展出KELM。在ELM上应用Mercer's条件为其定义一个核矩阵
| $ \left\{\begin{array}{l} \boldsymbol{\varOmega}_{E L M}=\boldsymbol{H} \boldsymbol{H}^{\mathrm{T}} \\ \boldsymbol{\varOmega}_{i, j}=h\left(x_{i}\right) \cdot h\left(x_{j}\right)=K\left(x_{i}, x_{j}\right) \end{array}\right., $ | (7) |
式中: K (xi, xj) 为核函数,h (·) 为隐含层神经元输出函数。选择常用的径向基函数(Radial Basis Function,RBF)作为核函数,其表达式为
| $ K\left(x_{i}, x_{j}\right)=\exp \left(-\left\|x_{i}-x_{j}\right\|^{2} / \gamma\right) $ | (8) |
式中: γ为核参数。然后由式(6)、(7)和(8)可得KELM的输出函数为
| $ \begin{gathered} f(\boldsymbol{x})= \\ h(\boldsymbol{x}) \boldsymbol{H}^{\mathrm{T}}\left(\frac{I}{C}+\boldsymbol{H} \boldsymbol{H}^{\mathrm{T}}\right)^{-1} \boldsymbol{Y}= \\ \left(\begin{array}{c} K\left(x, x_{1}\right) \\ K\left(x, x_{2}\right) \\ \vdots \\ K\left(x, x_{N}\right) \end{array}\right)^{\mathrm{T}}\left(\frac{\boldsymbol{I}}{C}+\boldsymbol{\varOmega}_{\mathrm{ELM}}\right)^{-1} \boldsymbol{Y} \end{gathered}。$ | (9) |
逐步浓缩上升工艺主要控制糖膏液位与锤度,煮糖过程中影响液位和锤度变化的因素有环境变量和操作变量2种: 环境变量包括当前糖膏液位、糖膏锤度、糖膏温度、蒸汽温度、蒸汽压力、真空度、入料锤度和入料温度;操作变量包括蒸汽阀和入料阀的开度。为实现预测控制目标,选择环境变量和操作变量作为KELM的输入变量,以糖膏液位和锤度的变化量为输出变量。
1.2.2 优化KELM参数由式(8)、(9)可知,KELM的性能受正则化参数C与核函数参数γ取值影响,为此采用PSO算法对二者进行优化以提高KELM的预测性能。PSO是一种基于鸟群觅食行为的随机全局优化技术,具有收敛速度快、易于实现的特点,被应用于多目标优化、模式识别和神经网络训练等领域[16, 17]。PSO将鸟群视为粒子质点集合,粒子个体的移动速度和方向由群体信息和个体运动历史信息决定。适应度是确定粒子最优位置的标准,每次迭代后更新最优信息,经过一次次迭代整个群体最终朝着适应度最佳的位置移动。假设在D维搜索空间中有一个粒子数为N粒子群,表示为x= (x1, x2, …, xN)。第i个粒子在空间中的速度为v i= (vi1, vi2, …, viD),x i= (xi1, xi2, …, xiD) 是其当前位置。每个粒子的速度和位置根据自身经历过的最佳位置p i= (pi1, pi2, …, piD) 和群体经历过的最佳位置p g= (pg1, pg2, …, pgD) 分别通过式(10)和式(11)进行更新。
| $ \begin{array}{l} \ \ \ \ \ \ \ \ v_{i d}^{t+1}=w v_{i d}^{t}+\eta_{1} r_{1}\left(p_{i d}^{t}-x_{i d}^{t}\right)+ \\ \eta_{2} r_{2}\left(p_{g d}^{t}-x_{i d}^{t}\right), \end{array} $ | (10) |
| $ x_{i d}^{t+1}=x_{i d}^{t}+v_{i d}^{t+1}, $ | (11) |
式中: 1≤i≤N,1≤d≤D,t为迭代次数,w为惯性权重,η1、η2为加速系数,r1、r2为0到1之间的随机数。在优化迭代过程中,个体最优和全局最优位置根据适应度分别利用式(12)、(13)进行更新。
| $ p_{i d}^{t+1}=\left\{\begin{array}{c} x_{i d}^{t+1}, \text { fitness }\left(x_{i d}^{t+1}\right)<\text { fitness }\left(p_{i d}^{t}\right) \\ p_{i d}^{t}, \text { fitness }\left(x_{i d}^{t+1}\right) \geqslant \text { fitness }\left(p_{i d}^{t}\right) \end{array}\right., $ | (12) |
| $ p_{g}=\min \left\{p_{1}^{t+1}, p_{2}^{t+1}, \cdots, p_{N D}^{t+1}\right\}, $ | (13) |
式中: fitness(·)为适应度函数。利用PSO优化KELM参数的流程如图 2所示。

|
| 图 2 PSO优化KELM参数流程图 Fig. 2 Flow chart of parameters optimization of KELM using PSO |
1.2.3 构建预测模型
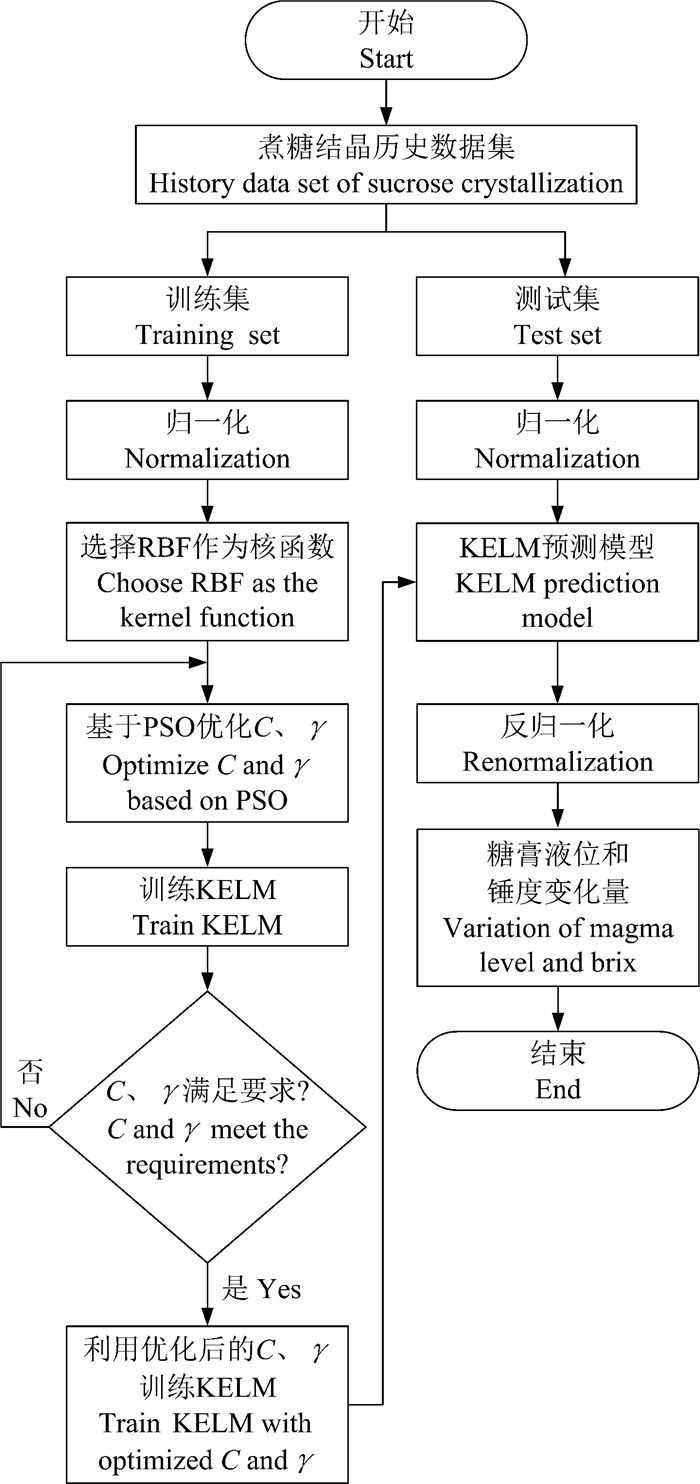
利用煮糖结晶历史数据,以环境变量和操作变量作为输入,以糖膏液位和锤度变化作为输出,基于KELM构建煮糖结晶预测模型,选择RBF作为KELM的核函数,并采用PSO算法优化KELM的正则化参数C和核函数参数γ。KELM预测模型的构建流程如图 3所示。
|
| 图 3 KELM预测模型构建流程图 Fig. 3 Flow chart of building KELM prediction model |
2 基于KELM的煮糖结晶自适应控制方法
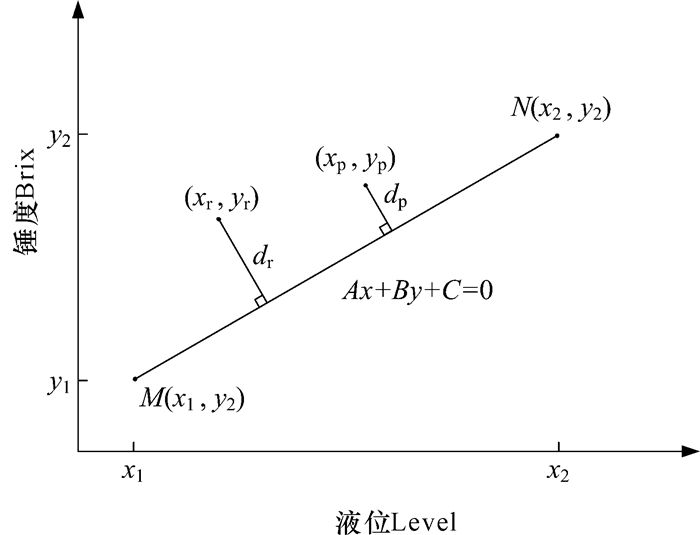
假设某煮糖阶段的工艺要求如图 4所示,M(x1, y1)、N(x2, y2)分别是工艺的起点与终点。平面空间内连接点M和点N的任一曲线均可能是实际的工艺过程,生产中期望糖膏液位和锤度沿线段MN同步上升以使工艺曲线最短,线段MN是该阶段的理想工艺曲线,将其记为
|
| 图 4 煮糖结晶工艺示意图 Fig. 4 Diagram of sucrose crystallization process |
| $ A x+B y+C=0 $ | (14) |
式中: A、B和C为常数,x1≤x≤x2,y1≤y≤y2。煮糖结晶通过控制蒸汽阀和入料阀的开度使糖膏液位和锤度的变化接近理想工艺曲线,工艺偏差用实际工艺点( xr, yr) 与理想工艺曲线的距离dr来衡量:
| $ d_{\mathrm{r}}=\frac{\left|A x_{\mathrm{r}}+B y_{\mathrm{r}}+C\right|}{\sqrt{A^{2}+B^{2}}}。$ | (15) |
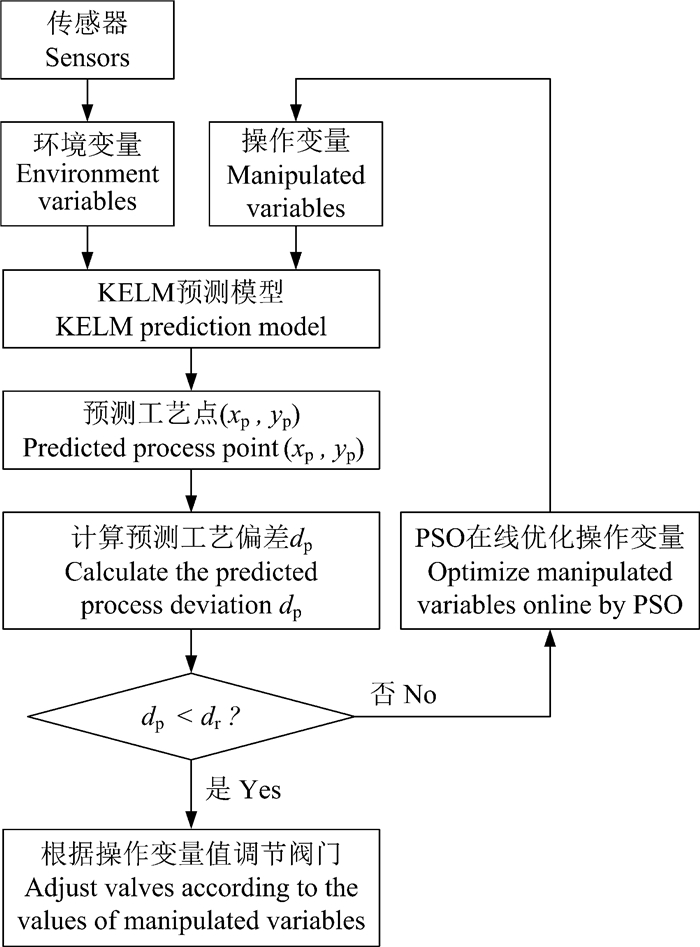
基于KELM预测模型预测糖膏液位和锤度的变化量Δx与Δy,可获得预测工艺点( xp, yp) = (xr+Δx, yr+Δy),将(xp, yp) 代入式(15)求出预测工艺偏差dp。煮糖结晶自适应控制方法利用传感器对环境变量进行周期性采样,采样间隔期以预测工艺偏差dp作为适应度函数,采用PSO优化KELM预测模型输入变量中的操作变量(蒸汽阀和入料阀开度),当dp < dr时根据优化的操作变量值自动调节阀门。而PSO算法通过迭代与比较获取操作变量全局最优解则需要较长的时间,但由于煮糖是一个时变过程,故较长的寻优时间可能导致操作变量全局最优解已经不适合当前结晶环境,为此根据PSO获取的操作变量局部最优解调节蒸汽阀和入料阀,然后进行下一次环境变量的采样和操作变量的优化,如此循环,进行滚动优化。煮糖结晶自适应控制过程如图 5所示。
|
| 图 5 煮糖结晶自适应控制流程图 Fig. 5 Flow chart of adaptive control for sucrose crystallization |
3 实验与结果分析 3.1 实验平台
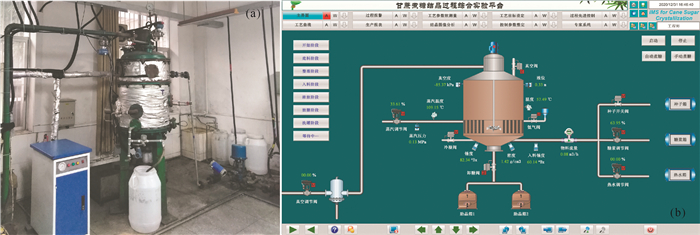
煮糖结晶过程综合实验平台如图 6所示。该平台主要由硬件和软件两部分组成: 硬件包括蒸汽发生器、结晶罐、物料箱、真空泵、电动阀门、传感器、采集模块和上位机等。软件包括基于KingSCADA组态软件开发的监控系统和采用MATLAB语言编写的自适应控制模块。监控系统与自适应控制模块之间通过组态软件OPC sever通讯,用于传递环境变量和操作变量信息。监控系统与采集模块之间采用modbus RTU协议通讯,将传感器测得的环境变量上传至上位机的实时数据库,同时传输操作变量信息用于调节阀门开度。
|
| (a) 实验平台硬件,(b) 实验平台监控系统界面 (a)Hardwares of experiment platform, (b)Monitoring system interface of experiment platform 图 6 煮糖结晶过程综合实验平台 Fig. 6 Comprehensive experiment platform for sucrose crystallization |
3.2 KELM预测模型的验证与分析
利用综合实验平台的煮糖历史数据集对KELM模型进行训练与测试,部分数据集如表 1所示,x1-x10依次为糖膏液位、糖膏锤度、糖膏温度、蒸汽温度、蒸汽压力、真空度、入料锤度、入料温度、蒸汽阀开度与入料阀开度,y1、y2为糖膏液位与锤度变化量。
| 序号 No. |
x1 (cm) |
x2 (°Bx) |
x3 (℃) |
x4 (℃) |
x5 (kPa) |
x6 (-kPa) |
x7 (°Bx) |
x8 (℃) |
x9 (%) |
x10 (%) |
y1 (cm) |
y2 (°Bx) |
| 1 | 30.24 | 80.00 | 55.06 | 110.59 | 31.75 | 83.05 | 59.83 | 55.81 | 16.00 | 45.00 | 0.01 | 0.39 |
| 2 | 30.24 | 80.39 | 54.85 | 110.16 | 30.32 | 83.06 | 59.88 | 55.71 | 16.00 | 45.00 | -0.11 | -0.06 |
| 3 | 30.13 | 80.33 | 54.60 | 110.04 | 29.32 | 83.03 | 59.96 | 56.16 | 16.00 | 45.00 | 0.12 | 0.21 |
| 4 | 30.25 | 80.54 | 54.36 | 110.97 | 28.39 | 83.03 | 60.00 | 56.16 | 16.00 | 45.00 | 0.29 | -0.12 |
| 5 | 30.54 | 80.42 | 54.12 | 110.39 | 30.53 | 83.02 | 60.12 | 55.83 | 16.00 | 45.00 | -0.06 | 0.25 |
| 6 | 30.49 | 80.67 | 54.11 | 110.07 | 30.46 | 83.02 | 59.99 | 55.98 | 16.00 | 45.00 | 0.14 | 0.21 |
| 7 | 30.63 | 80.88 | 54.06 | 109.64 | 28.69 | 83.04 | 60.00 | 56.14 | 16.00 | 45.00 | -0.35 | -0.13 |
| 8 | 30.28 | 80.75 | 53.97 | 109.27 | 28.25 | 83.07 | 60.03 | 56.17 | 16.00 | 45.00 | 0.19 | 0.09 |
| 9 | 30.47 | 80.84 | 53.93 | 109.15 | 31.29 | 83.05 | 60.04 | 56.00 | 16.00 | 45.00 | 0.20 | 0.06 |
| 10 | 30.67 | 80.90 | 53.85 | 109.00 | 29.05 | 83.08 | 60.04 | 56.08 | 16.00 | 45.00 | -0.18 | 0.05 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 367 | 59.98 | 93.13 | 61.29 | 109.38 | 33.38 | 85.33 | 60.44 | 66.73 | 10.00 | 15.00 | 0.17 | 0.05 |
从历史数据集中随机选择245组构成训练集,用于训练KELM模型,余下122组作为测试集用于评估训练后模型的预测性能。训练集和测试集的输入、输出变量均归一化到[-1, 1]。利用训练集和PSO算法对模型的正则化参数C和核函数参数γ进行寻优,以输出变量的均方根误差(RMSE)作为适应度,寻优范围为0到1 024,粒子种群规模为50,最大迭代次数为200,惯性权重w=0.6,加速系数η1=η2=1.5。参数寻优的结果如表 2所示。
| 输出变量 Output variable |
RMSE | 正则化参数C Regularization parameter C |
核参数γ Kernel parameter γ |
| 液位变化Level variation | 0.050 2 | 975.153 8 | 1.763 0 |
| 锤度变化Brix variation | 0.015 8 | 903.265 9 | 29.810 3 |
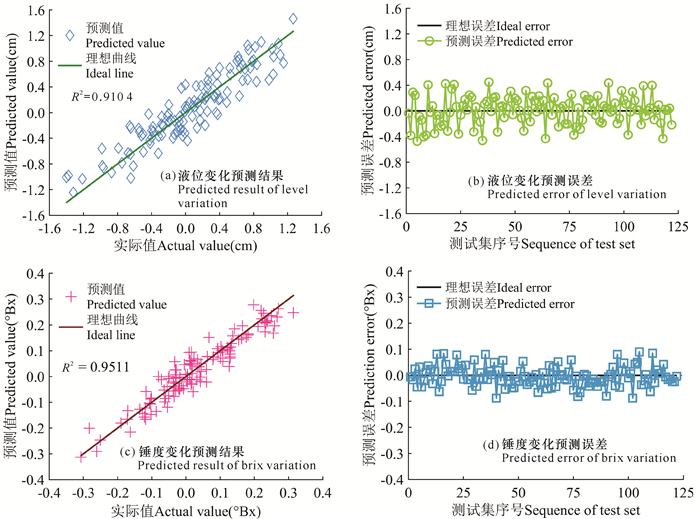
利用优化后的正则化参数C和核函数参数γ构建KELM预测模型,使用测试集进行模型的预测性能评估,结果如图 7所示。
|
| 图 7 KELM模型的预测结果 Fig. 7 Predictive results of KELM model |
图 7a和图 7c为液位和锤度变化量的预测回归图,可以看到预测值数据点紧密地分布在回归线两侧,不存在远离回归线的极端点,决定系数R2较接近于1。图 7b和图 7d显示预测误差较为平稳,其中液位变化量的最大绝对误差、平均绝对误差和均方根误差分别为0.472 0,0.178 2,0.222 8 cm;锤度变化量的最大绝对误差、平均绝对误差和均方根误差分别为0.090 3,0.031 7,0.039 5°Bx。液位和锤度变化量的预测值与实际值吻合良好,表明KELM预测模型具有良好的泛化性能和预测能力。在难以获得精确机理模型的情况下,KELM预测模型建立了环境变量、操作变量与糖膏液位、锤度变化量之间的黑箱模型,模型的预测值与实际值具有较高的拟合度,因而选择该模型对煮糖结晶过程进行预测控制。
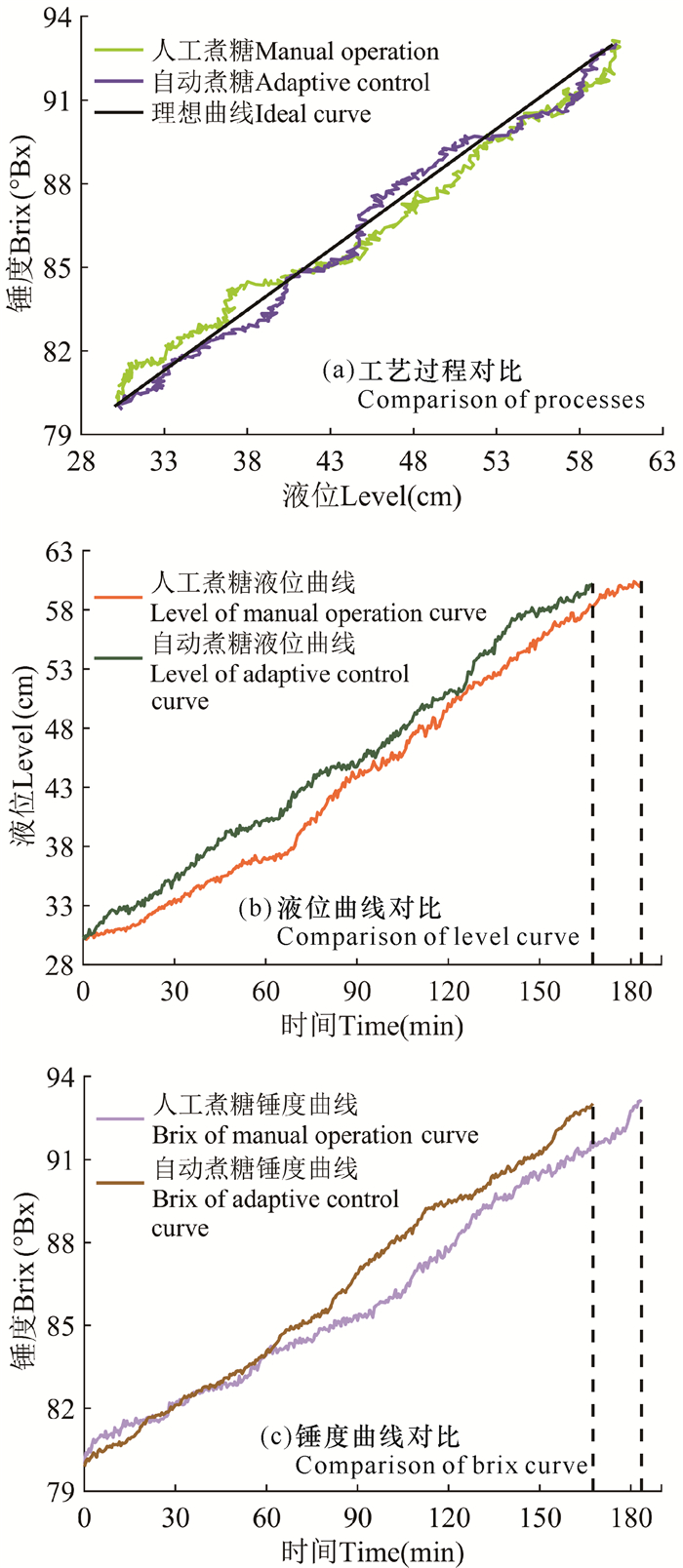
3.3 煮糖结晶自适应控制实验效果分析煮糖自适应控制实验实时采集环境变量和操作变量数据输入KELM预测模型,模型输出糖膏液位和锤度变化量预测值,利用该预测值计算预测工艺点和预测工艺偏差,通过PSO算法在线滚动优化操作变量使预测工艺偏差小于当前工艺偏差,并根据优化后的操作变量信息调节蒸汽阀和入料阀,实现对理想工艺曲线的跟踪。利用综合实验平台进行自动煮糖实验,将其工艺过程与人工煮糖工艺过程进行对比,结果如图 8所示。
|
| 图 8 自动与人工煮糖工艺对比 Fig. 8 Comparison of automatic and manual sucrose crystallization process |
从图 8a中可以看到,自动煮糖工艺过程比人工煮糖工艺过程整体上更接近理想工艺曲线。人工煮糖的最大工艺偏差和平均工艺偏差分别为1.521 1,0.564 9,自动煮糖的最大工艺偏差和平均工艺偏差分别为1.124 9,0.392 0。由于自动煮糖的操作变量优化以KELM模型的预测输出作为前提,预测模型存在预测误差,导致自动煮糖工艺过程呈现波动状态,但波动幅度小于人工煮糖工艺过程,这表明预测模型具有的预见性使得优化后的操作变量比人工设定的更有利于实现对理想工艺曲线的跟踪。图 8b与图 8c显示自动煮糖的液位和锤度曲线波动较小,说明预测控制策略可以较好地控制煮糖过程糖膏液位和锤度的变化,同时自动煮糖达到卸糖液位和锤度所需的时间比人工煮糖少13 min,相对减少7.06%,证明基于KELM预测模型的煮糖结晶自适应控制方法是可行和有效的。
4 结论为研究煮糖结晶过程的自适应控制问题,基于KELM构建煮糖过程环境变量、操作变量与糖膏液位、锤度变化量之间的预测模型,利用煮糖历史数据进行训练与测试,结果显示,KELM模型获得较高的训练精度并具有良好的泛化性能。在KELM预测模型的基础上,通过实时采集煮糖过程的环境变量和操作变量,采用PSO算法在线滚动优化操作变量,使预测工艺输出接近理想工艺曲线,并利用优化后的操作变量控制阀门,实现煮糖过程的自适应控制。与人工煮糖相比,采用自适应控制的煮糖工艺过程整体上更接近理想工艺曲线,且达到卸糖液位和锤度所需的时间减少,证明了基于KELM预测模型的煮糖结晶自适应控制方法的可行性和有效性。
| [1] |
黄赞, 姚耀文. 基于Fuzzy-PID的糖厂煮糖结晶控制系统设计[J]. 食品科技, 2005(12): 42-44. DOI:10.3969/j.issn.1005-9989.2005.12.014 |
| [2] |
DAMOUR C, BENNE M, BOILLEREAUX L, et al. Multivariable linearizing control of an industrial sugar crystallization process[J]. Journal of Process Control, 2011, 21(1): 46-54. DOI:10.1016/j.jprocont.2010.10.002 |
| [3] |
潘泽锴. 蔗糖结晶过程控制节点设计与研究[J]. 食品与机械, 2016, 32(7): 89-92. |
| [4] |
邹志云, 王志甄, 于蒙, 等. 非线性模型预测控制技术的研究现状与发展趋势探讨[J]. 计算机与应用化学, 2018, 35(1): 7-17. |
| [5] |
王浩坤, 徐祖华, 赵均, 等. 无偏模型预测控制综述[J]. 自动化学报, 2020, 46(5): 858-877. |
| [6] |
BEYOU S, GRONDIN-PEREZ B, BENNE M, et al. Control improvement of a C sugar cane crystallization using an auto-tuning PID controller based on linearization of a neural network[J]. World Academy of Science, Engineering and Technology, 2009, 54: 190-195. |
| [7] |
杨继君, 徐辰华, 孔繁镍. 煮糖结晶过程的多模型动态矩阵控制研究[J]. 计算机与应用化学, 2006, 23(11): 1105-1108. DOI:10.3969/j.issn.1001-4160.2006.11.018 |
| [8] |
GEORGIEVA P, DE AZEVEDO S F. Neural network-based control strategies applied to a fed-batch crystallization process[J]. International Journal of Computational Intelligence, 2006, 3(3): 224-233. |
| [9] |
DAMOUR C, BENNE M, GRONDIN-PEREZ B, et al. Nonlinear predictive control based on artificial neural network model for industrial crystallization[J]. Journal of Food Engineering, 2010, 99(2): 225-231. DOI:10.1016/j.jfoodeng.2010.02.027 |
| [10] |
SUÁREZ L A P, GEORGIEVA P, AZEVEDO S F. Nonlinear MPC for fed-batch multiple stages sugar crystallization[J]. Chemical Engineering Research and Design, 2011, 89(6): 753-767. DOI:10.1016/j.cherd.2010.10.010 |
| [11] |
韦锦, 蓝启亮, 蒙艳玫, 等. 基于子空间模型的煮糖结晶过程入料流量自适应控制[J]. 广西大学学报: 自然科学版, 2018, 43(5): 1786-1793. |
| [12] |
ALBADRA M, TIUNA S. Extreme learning machine: A review[J]. International Journal of Applied Engineering Research, 2017, 12(14): 4610-4623. |
| [13] |
徐睿, 梁循, 齐金山, 等. 极限学习机前沿进展与趋势[J]. 计算机学报, 2019, 42(7): 1640-1670. |
| [14] |
ZHANG L, ZHANG D. Evolutionary cost-sensitive extreme learning machine[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(12): 3045-3060. DOI:10.1109/TNNLS.2016.2607757 |
| [15] |
HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Transactions on Systems Man & Cybernetics: Part B (Cybernetics), 2012, 42(2): 513-529. |
| [16] |
JAIN N K, NANGIA U, JAIN J. A review of particle swarm optimization[J]. Journal of the Institution of Engineers (India): Series B, 2018, 99(4): 407-411. |
| [17] |
张雁茹, 赵志刚, 李永恒. 基于扰动的自适应粒子群优化算法[J]. 广西科学, 2017, 24(3): 258-262. |



