氧化锌(ZnO)是一种宽禁带的半导体材料,因其优良的光电性质而备受关注,有着较长的研究历史。许多研究组曾利用第一性原理对ZnO材料进行理论研究,比如关于ZnO基本电子结构性质、光学性质和磁学性质的研究[1-4],关于元素掺杂ZnO的性质研究[5-8],以及关于ZnO本征缺陷的研究[9-11]等, 但目前还没有关于利用不同晶格优化方法优化ZnO原胞结构的研究报道。
准确的结构优化是获取可信材料性质的前提。VASP是一款基于第一性原理计算方法的材料性质计算程序包,在材料计算研究中有着广泛的应用[12-14]。VASP程序包中也提供了多种晶体优化的方法。一般来说,状态方程拟合法可以得到更准确的结果,但过程非常繁琐;自动优化法的结果会有所偏差,但过程方便简单。2种优化方法的对比研究未见有前人报道。
对于很多研究者,特别是初学者而言,常因如何选择合适的晶格优化方法而困扰。本文以ZnO原胞作为晶格优化对象,采用VASP计算程序包,分别使用状态方程拟合法和自动优化法对ZnO原胞进行晶格优化,对比研究2种优化方法所得到晶格体积和晶格参数的差异,并研究在不同的初始原胞体积下,自动优化法所得结果的差异,为一般材料的晶格体积优化方法的选择提供一定指导和参考。
1 计算方法本文使用基于密度泛函理论(DFT)[15]的第一性原理方法来研究ZnO晶体体积的优化方法,其中使用VASP计算程序包进行晶格优化,使用VESTA[16]软件进行ZnO原胞模型构建以及晶格参数的读取。在具体优化过程中,采用超软赝势(USPP)来描述电子与离子的交换作用,使用PW91形式的交互关联泛函来处理关联作用,系统总能量的收敛判据为1×10-5 eV/atom,力收敛判据为1×10-3 eV/Å,布里渊区k点网格取样采用Gamma方法。k网格数目(KPOINTS)以及平面波截断能(ENCUT)在不同优化方法下进行具体的优化后选取。所有计算都进行2次计算:一次结构优化计算,一次静态计算。读取静态计算得到的能量作为体系能量。
KPOINTS取值的优化方法如下:设置ENCUT为500 eV,KPOINTS分别取点3×3×3,4×4×4,5×5×5,6×6×6,7×7×7,8×8×8,9×9×9,10×10×10,11×11×11,12×12×12,13×13×13,14×14×14,15×15×15,计算并绘制体系能量和KPOINTS取值的关系图,然后根据关系图选取合适的KPOINTS值。
ENCUT取值的优化方法如下:设置KPOINTS为9×9×9,ENCUT取值分别为350,400,450,500,550,600 eV,计算并绘制体系能量和ENCUT取值的关系图,然后根据关系图选取合适的ENCUT值。
ZnO原胞模型的构建方法如下:使用VESTA软件构建纤锌矿ZnO的原胞模型,其空间群为P63mc (NO.186),每个纤锌矿ZnO原胞包含4个原子(其中2个Zn原子,2个O原子),Zn原子与O原子各自以密堆积的方式排列,Zn原子位于相邻4个O原子所形成的四面体中心,O原子位于相邻4个Zn原子所形成的四面体中心。ZnO原胞的晶格参数参考多篇实验研究数据[17-21]后选取,采用的晶格参数为a=b=3.249 3 Å,c=5.205 4 Å, α=β=90°, γ=120°。
状态方程拟合法优化ZnO原胞的步骤如下:设置参数ISIF=2,即在优化过程中保持晶格体积不变,只优化离子位置。对ENCUT和KPOINTS参数进行优化测试后选定ENCUT和KPOINTS的取值。在保持原始晶格c/a=1.602不变的情况下,对原胞体积进行缩放,缩放系数分别为0.80,0.85,0.90,0.95,1.00,1.05,1.10,1.15,1.20。经过缩放后,初始体积发生了变化,计算并绘制体系能量与体积之间的关系图(E-V图)。然后根据Brich-Murnaghan状态方程[22](BM状态方程)对E-V图进行拟合,得到平衡体积V0,其中BM状态方程如下:
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;E\left( V \right) = {E_0} + \frac{{9{V_0}{B_0}}}{{16}}{{\left\{ {\left[ {{{\left( {\frac{{{V_0}}}{V}} \right)}^{\frac{2}{3}}} - 1} \right]} \right.}^3}{B_0}^\prime + }\\ {{{\left[ {{{\left( {\frac{{{V_0}}}{V}} \right)}^{\frac{2}{3}}} - 1} \right]}^2}\left. {\left[ {6 - 4{{\left( {\frac{{{V_0}}}{V}} \right)}^{\frac{2}{3}}}} \right]} \right\},} \end{array} $ | (1) |
其中V0,E0,B0, B′0分别为平衡体积、平衡态能量、平衡态弹性模量和弹性模量的一阶导数。最后将得到的平衡体积再次进行优化计算,得到晶格参数。
自动优化法优化ZnO原胞的步骤如下:设置参数ISIF=3,即在优化过程中同时优化晶格的体积和离子位置。对ENCUT和KPOINTS参数进行优化测试后,选定ENCUT和KPOINTS的取值,直接对ZnO原胞进行晶格优化,即可得到优化后的晶格体积和晶格参数。
测试不同初始体积下自动优化法优化结果的步骤如下:设置ISIF=3,ENCUT和KPOINTS参数选取测试后的取值,在保持原始晶格c/a=1.602不变的情况下,对初始体积进行缩放,缩放系数分别为0.80,0.85,0.90,0.95,1.00,1.05,1.10,1.15,1.20,得到不同初始体积的ZnO原胞。直接对不同初始体积的ZnO原胞进行晶格优化计算,得到优化的结果。
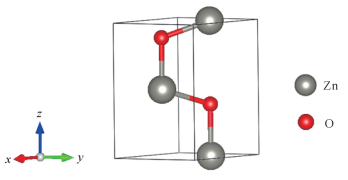
2 结果与分析 2.1 ZnO原胞模型的构建图 1是在VESTA软件中构建的纤锌矿ZnO原胞模型,其中灰色大球代表锌(Zn)原子,红色小球代表氧(O)原子。
|
| 图 1 纤锌矿ZnO原胞模型 Fig. 1 Model of wurzite ZnO primitive cell |
2.2 状态方程拟合法 2.2.1 KPOINTS和ENCUT参数优化
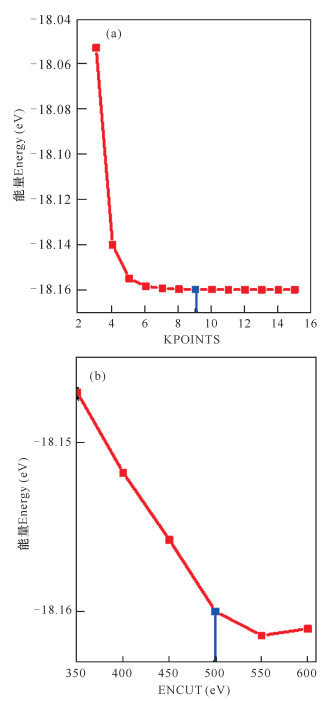
在设定ISIF=2的情况下,优化KPOINTS和ENCUT参数,以保证计算过程能够稳定地收敛。图 2a为ISIF=2时,体系能量(Energy)随KPOINTS取值的变化,其中横坐标数字n代表KPOINTS取值为n×n×n (n从3变化到15)。从图 2a可以知道,随着KPOINTS取值的增大,整个体系的能量逐渐降低。在KPOINTS取值为6×6×6以上,整个系统的能量基本趋于稳定,说明KPOINTS取值大于6×6×6,系统计算就可以达到很好的收敛效果。KPOINTS取值越大,计算结果越精确,但同时所需要的计算量也越大。综合考虑,在此部分计算中KPOINTS取值为9×9×9。
|
| 图 2 ISIF=2时, 体系能量随KPOINTS和ENCUT取值的变化 Fig. 2 When ISIF=2, the system energy changes with the values of KPOINTS and ENCUT |
图 2b为ISIF=2时,体系能量随ENCUT取值的变化。从图 2b可知,随着ENCUT取值增大,体系能量逐渐降低,最后达到稳定平衡状态。当ENCUT取值由500 eV变到550 eV时,能量变化只有1.4×10-3 eV,说明当ENCUT取值为500 eV时,系统计算已经达到很好的收敛效果。随着ENCUT取值变大,计算量也会随之增大。综合考虑,在此部分的计算中,ENCUT的取值为500 eV。
2.2.2 E-V图拟合选取优化后的计算参数(KPOINTS取值为9×9×9,ENCUT取值为500 eV), 在保持晶体c/a=1.602不变的情况下,对体积进行缩放,初始原胞的体积为47.595 3 Å3。缩放后对应的晶体体积为24.368 8,29.229 5,34.697 0,40.807 0,47.595 3,55.097 5,63.349 3,72.386 5,82.244 6 Å3。
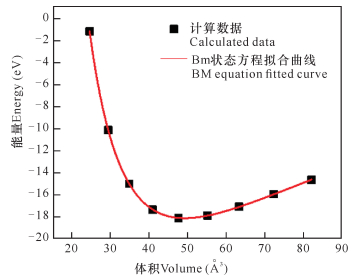
图 3为体系能量随晶体体积的变化情况,即E-V图。从图 3可以明显看出,体系能量随着晶体体积的增大呈现先减少后增加的“碗状”变化:体积从24.368 8 Å3增大到47.595 3 Å3的过程中,整个体系能量逐渐降低,而体积从47.595 3 Å3增大到82.244 6 Å3的过程中,整个体系能量是逐渐增加的。根据BM状态方程的拟合,得到平衡体积V0=49.206 2 Å3,在平衡体积的条件下再次进行晶格优化, 得到晶格常数a=b=3.285 6 Å,c=5.263 5 Å。状态方程拟合法优化结束后,ZnO原胞仍然保持纤锌矿的结构。
|
| 图 3 体系能量随晶体体积的变化 Fig. 3 Change of system energy with crystal volume |
实验过程中,合成方法环境温度以及形貌等因素都会对ZnO晶格参数产生影响,不同实验组测量得到的ZnO晶格常数也会有所区别[17-21]。部分实验组测量的实验数据见表 1。由于ZnO原胞建模时所采用的晶格参数是参考多篇实验数值获得,故采用建模时所使用的晶格参数a=b=3.249 3 Å,c=5.205 4 Å,体积V=47.595 3 Å3作为ZnO实验参考值来对计算优化的数值进行分析比较。相比于实验参考值,状态方程拟合法得到的晶格常数a,b,c均偏大,误差都为1.12%,晶体体积的误差为3.38%。综上可见,晶格常数的误差在2%内,晶体体积的误差在4%内,属于合理的误差范围,证明计算结果的可靠性。
2.3 自动优化法 2.3.1 计算参数的优化
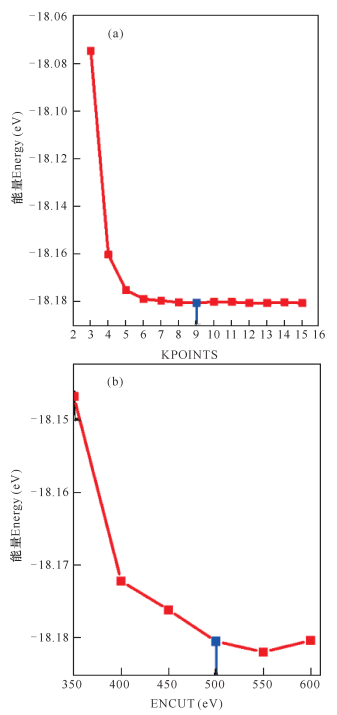
图 4a为ISIF=3时, 体系能量随KPOINTS取值的变化,其中横坐标数字n代表KPOINTS取值为n×n×n (n从3变化到15)。从图 4a可以知道,随着KPOINTS取值增大,整个体系能量逐渐降低。在KPOINTS取值为6×6×6以上,整个系统的能量基本趋于稳定,说明KPOINTS取值大于6×6×6,系统计算就可以达到很好的收敛效果。KPOINTS取值越大,计算结果越精确,同时所需要的计算量也越大。综合考虑,在此部分计算中KPOINTS取值为9×9×9。
|
| 图 4 ISIF=3时, 体系能量随KPOINTS和ENCUT取值的变化 Fig. 4 When ISIF=3, the system energy changes with the values of KPOINTS and ENCUT |
图 4b为ISIF=3时,体系能量随ENCUT取值的变化。从图 4b可知,随着ENCUT取值增大,体系能量逐渐降低,最后达到稳定平衡状态。当ENCUT取值由500 eV变到550 eV时,能量变化只有1.4×10-3 eV,说明当ENCUT取值为500 eV时,系统的能量基本达到最小值并趋于稳定,说明此时系统计算可以达到很好的收敛效果。随着ENCUT的取值变大,计算量也会随之增大。综合考虑,在此部分的计算中,ENCUT的取值为500 eV。
2.3.2 自动优化的结果在VASP的计算中,设置ISIF=3,即在晶格优化过程中,计算系统会同时优化离子位置和晶格体积。自动优化结束后,ZnO原胞仍保持纤锌矿结构,晶格常数a=b=3.282 0 Å,c=5.260 1 Å,晶格体积为49.068 4 Å3。与实验参考值相比,晶格常数a,b的误差为1.01%,晶格常数c的误差为1.05%,晶体体积的误差为3.1%,均属于合理的误差范围,证明计算结果的可靠性。与状态方程拟合法得到的参数相比,自动优化法晶格常数a,b的误差为0.11%,晶格常数c的误差为0.06%,晶体体积的误差为0.28%。2种优化方法的结果相近,所以对于一般晶格的优化,直接采用方便快捷的自动优化法即可。
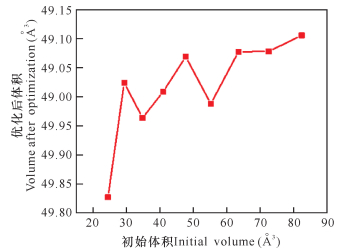
2.3.3 不同初始体积下自动优化的结果为进一步研究不同的初始体积下使用自动优化法对最后计算结果是否有影响,本文首先通过不同的缩放系数得到不同的晶格初始体积,再通过系统自动优化得到晶格参数。初始的晶体体积分别为24.368 8,29.229 5,34.697 0,40.807 0,47.595 3,55.097 5,63.349 3,72.386 5,82.244 6 Å3。图 5为自动优化得到的晶体体积随不同初始体积的变化情况。由图 5可以看出,整体而言,随着初始体积的增加,优化后体积一直在波动,无明显的函数关系。
|
| 图 5 自动优化后的晶格体积随初始体积的变化 Fig. 5 Change of lattice volume with initial volume after automatic optimization |
不同初始体积条件下自动优化得到的晶格参数见表 2。对于不同的晶格初始体积,优化后的体积为48.826 0-49.108 4 Å3;晶格常数a,b为3.267 4-3.286 9 Å;晶格常数c为5.239 8-5.296 8 Å。
| 初始体积 Initial volumes (Å3) |
优化后体积 Volume after optimization (Å3) |
晶格常数 Lattice constants a, b (Å) |
晶格常数 Lattice constant c (Å) |
| 24.368 8 | 48.826 0 | 3.270 0 | 5.272 6 |
| 29.229 5 | 49.025 1 | 3.286 9 | 5.239 8 |
| 34.697 0 | 48.972 1 | 3.267 4 | 5.296 8 |
| 40.807 0 | 49.008 6 | 3.273 1 | 5.282 3 |
| 47.595 3 | 49.068 4 | 3.282 0 | 5.260 1 |
| 55.097 5 | 48.988 2 | 3.278 6 | 5.262 4 |
| 63.349 3 | 49.079 6 | 3.276 4 | 5.279 3 |
| 72.386 5 | 49.078 1 | 3.275 7 | 5.281 4 |
| 82.244 6 | 49.108 4 | 3.275 1 | 5.286 6 |
不同初始体积下自动优化法得到的晶格参数与实验参考值的误差见表 3。从表 3可以看出,对比实验参考值,不同初始体积自动优化得到的晶格体积的误差为2.59%- 3.18%,晶格常数a,b的误差为0.56%-1.16%,晶格常数c的误差为0.66%-1.76%,都在合理的误差范围内,证明在不同的初始体积下,自动优化法仍能给出合理的优化结果。
| 初始体积 Initial volumes (Å3) |
误差Errors (%) | ||
| 优化后体积 Volume after optimization |
晶格常数a, b Lattice constants a, b |
晶格常数c Lattice constant c |
|
| 24.368 8 | 2.59 | 0.64 | 1.29 |
| 29.229 5 | 3.00 | 1.16 | 0.66 |
| 34.697 0 | 2.89 | 0.56 | 1.76 |
| 40.807 0 | 2.97 | 0.73 | 1.48 |
| 47.595 3 | 3.10 | 1.01 | 1.05 |
| 55.097 5 | 2.93 | 0.90 | 1.10 |
| 63.349 3 | 3.12 | 0.83 | 1.42 |
| 72.386 5 | 3.12 | 0.81 | 1.46 |
| 82.244 6 | 3.18 | 0.79 | 1.56 |
不同初始体积下自动优化法得到的晶格参数与状态方程拟合值的误差见表 4。从表 4可以看出,对比状态方程拟合值,不同初始体积自动优化得到的晶格体积误差为0.20%-0.77%,晶格常数a,b的误差为0.04%-0.55%,晶格常数c的误差为0.02%-0.63%。整体误差不超过1%,证明在不同晶格初始体积的条件下,自动优化法仍然能给出与状态方程拟合法相似的结果。由此进一步说明,对于类似ZnO原胞晶格体系的优化,采用方便简单的自动优化法取代状态方程拟合法是可行的。
| 初始体积 Initial volumes (Å3) |
误差Errors (%) | ||
| 优化后体积 Volume after optimization |
晶格常数a, b Lattice constants a, b |
晶格常数c Lattice constant c |
|
| 24.368 8 | 0.77 | 0.47 | 0.17 |
| 29.229 5 | 0.37 | 0.04 | 0.45 |
| 34.697 0 | 0.48 | 0.55 | 0.63 |
| 40.807 0 | 0.40 | 0.38 | 0.36 |
| 47.595 3 | 0.28 | 0.11 | 0.06 |
| 55.097 5 | 0.44 | 0.21 | 0.02 |
| 63.349 3 | 0.26 | 0.28 | 0.30 |
| 72.386 5 | 0.26 | 0.30 | 0.34 |
| 82.244 6 | 0.20 | 0.32 | 0.44 |
3 结论
与实验参考值相比,2种优化方法得到的晶格常数误差不超过2%,晶体体积误差不超过4%,属于合理的误差范围,2种优化方法都能得到比较合理的晶体参数结果。使用状态方程拟合法和自动优化法优化得到的晶格体积之间的误差为0.28%,晶格常数a,b的误差为0.11%,晶格常数c的误差为0.06%。在不同的初始体积下,自动优化法的结果随着初始体积的增加无明显变化关系。与状态方程拟合值相比,在不同的初始体积下使用自动优化法得到的晶格体积误差为0.20%-0.77%,晶格常数a,b的误差为0.04%-0.55%,晶格常数c的误差为0.02%-0.63%,误差都不超过1%。可见,对于类似ZnO原胞简单晶格体系的优化,完全可以使用系统自动优化法代替状态方程拟合法。本研究结果为晶格体积优化方法的选择提供了一定的理论参考价值。
| [1] |
FENG C, CHEN Z Y, LI W B, et al. First-principle calculation of the electronic structures and optical properties of the metallic and nonmetallic elements-doped ZnO on the basis of photocatalysis[J]. Physica B:Condensed Matter, 2019, 555: 53-60. DOI:10.1016/j.physb.2018.11.043 |
| [2] |
KALAY M, KART H H, KARTS O, et al. Elastic properties and pressure induced transitions of ZnO polymorphs from first-principle calculations[J]. Journal of Alloys and Compounds, 2009, 484(1): 431-438. |
| [3] |
ZHANG Z Y. Strain engineering for ZnO nanowires:First-principle calculations[J]. Physics Letters A, 2014, 378(16/17): 1174-1179. |
| [4] |
LIU C R, LI J B. Thermoelectric properties of ZnO nanowires:A first principle research[J]. Physics Letters A, 2011, 375(30/31): 2878-2881. |
| [5] |
SHEN L, WU R Q, PAN H, et al. Mechanism of ferromagnetism in nitrogen-doped ZnO:First-principle calculations[J]. Physical Review B, 2008, 78(7): 073306. DOI:10.1103/PhysRevB.78.073306 |
| [6] |
ZHANG X D, GUO M L, SHEN Y Y, et al. Electronic structure and optical transition in heavy metal doped ZnO by first-principle calculations[J]. Computational Materials Science, 2012, 54: 75-80. DOI:10.1016/j.commatsci.2011.10.003 |
| [7] |
BAI S L, GUO T, ZHAO Y B, et al. Mechanism enhancing gas sensing and first-principle calculations of Al-doped ZnO nanostructures[J]. Journal of Materials Chemistry A, 2013, 1(37): 11335-11342. DOI:10.1039/c3ta11516j |
| [8] |
XIE F W, YANG P, LI P, et al. First-principle study of optical properties of (N, Ga) codoped ZnO[J]. Optics Communications, 2012, 285(10/11): 2660-2664. |
| [9] |
LYONS J L, VARLEY J B, STIAUF D, et al. First-principles characterization of native-defect-related optical transitions in ZnO[J]. Journal of Applied Physics, 2017, 122(3): 035704. DOI:10.1063/1.4992128 |
| [10] |
BOVHYRA R V, POPOVYCH D I, BOVGYRA O V, et al. First principle study of native point defects in (ZnO)n nanoclusters (n=34, 60)[J]. Applied Nanoscience, 2019, 9(5): 1067-1074. DOI:10.1007/s13204-018-0706-z |
| [11] |
ZHENG F B, ZHANG C W, WANG P J, et al. The electronic and magnetic properties with intrinsic defects in ZnO nanosheets:First-principles prediction[J]. Current Applied Physics, 2013, 13(4): 799-802. DOI:10.1016/j.cap.2012.12.008 |
| [12] |
宁华, 李柳杰, 王旭坡, 等. Nb(100)表面吸附和解离氮气的密度泛函理论计算[J]. 广西科学, 2014, 21(3): 236-240. |
| [13] |
陶小马, 姚佩, 刘科成, 等. Ta-C化合物物理性质的第一性原理研究[J]. 广西科学, 2017, 24(6): 545-550. |
| [14] |
韦柳婷, 童张法, 吴东海, 等. 氧化钙(100)、(110)和Ca-terminated(111)表面性能的第一性原理研究[J]. 广西科学, 2015, 22(6): 670-674, 680. DOI:10.3969/j.issn.1005-9164.2015.06.018 |
| [15] |
HOHENBERG P, KOHN W. Inhomogeneous electron gas[J]. Physical Review B, 1964, 136(3B): 864-871. DOI:10.1103/PhysRev.136.B864 |
| [16] |
MOMMA K, IZUMI F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data[J]. Journal of Applied Crystallography, 2011, 44(6): 1272-1276. DOI:10.1107/S0021889811038970 |
| [17] |
SCHREYER M, GUO L, THIRUNAHARI S, et al. Simultaneous determination of several crystal structures from powder mixtures:The combination of powder X-ray diffraction, band-target entropy minimization and rietveld methods[J]. Journal of Applied Crystallography, 2014, 47(2): 659-667. DOI:10.1107/S1600576714003379 |
| [18] |
BUNN C W. The lattice-dimensions of zinc oxide[J]. Proceedings of the Physical Society, 1935, 47(5): 835-842. DOI:10.1088/0959-5309/47/5/307 |
| [19] |
GRAY T J. Sintering of zinc oxide[J]. Journal of the American Ceramic Society-Gray, 1954, 37(11): 534-539. DOI:10.1111/j.1151-2916.1954.tb13985.x |
| [20] |
REEBER R R. Lattice parameters of ZnO from 4.2° to 296°K[J]. Journal of Applied Physics, 1970, 41(13): 5063-5066. DOI:10.1063/1.1658600 |
| [21] |
CIMINO A, MAZZONE G, PORTA P. A lattice parameter study of defective zinc oxide[J]. Zeitschrift Für Physikalische Chemie, 1964, 41(3/4): 154-172. |
| [22] |
BIRCH F. The effect of pressure upon the elastic parameters of isotropic solids, according to Murnaghan's theory of finite strain[J]. Journal of Applied Physics, 1938, 9(4): 279-288. DOI:10.1063/1.1710417 |



