2. 柳州铁道职业技术学院, 广西柳州 545616;
3. 广西民族大学人工智能学院, 广西南宁 530006
2. Liuzhou Railway Vocational Technical College, Liuzhou, Guangxi, 545616, China;
3. College of Artificial Intelligence, Guangxi University for Nationnalities, Nanning, Guangxi, 530006, China
由于群智能算法无需先验知识,无需分析数据内部规律和内在关联,只需对数据本身进行学习,自组织、自适应地完成优化问题的求解,近年来大批群智能算法被相继提出,如布谷鸟搜索算法(Cuckoo Search Algorithm, CS)[1]、樽海鞘群算法(Salp Swarm Algorithm, SSA)[2]、狼群算法(Grey Wolf Optimizer, GWO)[3]、正弦余弦算法(Sine Cosine Algorithm, SCA)[4]、鲸鱼优化算法(Whale Optimization Algorithm)[5]、花朵授粉算法(Flower Pollenation Algorithm, FPA) [6]等。这些群智能算法基本上是模拟生物的群体行为,按照某种合作方式一起求解优化问题,并在工程优化、图像处理、特征选择和机器学习等领域得到广泛应用。蝴蝶优化算法(Butterfly Optimization Algorithm, BOA)[7]是模拟自然界的蝴蝶觅食或求偶行为而衍生出的一种仿生群智能算法,已成功解决图像分割[8]、经济负荷调度[9]等问题。但基本BOA也存在收敛速度慢、计算精度差和易陷入局部最优等缺陷,许多学者提出不同改进策略。如高文欣等[10]首先引入limit阈值来限定BOA陷入局部最优次数,然后结合单纯形法和正弦余弦算法提升算法性能,但同时也增加了算法时间复杂度且其函数4求解精度较低。王依柔等[11]首先在自身认知部分引入自适应惯性权重,其次在全局最优位置引入扰动策略,在花蜜位置引入疯狂因子来平衡算法的局部与全局搜索能力,提出无限折叠迭代混沌映射的蝴蝶优化算法(SIBOA),但该优化后的算法其精度还有待于进一步提升。宁杰琼等[12]首先利用Circle映射初始化种群,然后在局部搜索阶段利用动态切换概率,控制改进正弦余弦算法与蝴蝶优化算法的转换,并在全局和局部位置引入自适应权重系数和逐维变异策略,从而改进算法的性能,使求解的精度较高。但该算法的测试函数较少且回避了最难求解的Rosenbrock函数测试。高文欣等[13]在全局位置引入柯西分布函数,在局部位置引入自适应权重因子,并引入动态切换概率来改进算法性能,但函数Apline未达到理论最优。高文欣等[14]引入收敛因子和黄金正弦指引机制来提升算法效果,但测试函数较少,精度还有待于进一步提升。谢聪等[15]融入差分进化策略和精英策略改进算法,但算法的串联操作相应地增加了算法的时间开销。
虽然上述算法在一定程度上提高了算法性能,但仍有提升空间。本文提出一种融合正弦余弦算法的蝴蝶优化算法(Sine Cosine Algorithm and Butterfly Optimization Algorithm,SCABOA),在BOA基础之上从以下4个方面进行改进:在蝴蝶自身认知部分引入非线性自适应因子;重新定义香味浓度计算公式;在局部搜索阶段引入改进的正弦余弦算法;为回避转换概率对算法的影响,将种群一分为二。
1 蝴蝶优化算法蝴蝶优化算法是模拟蝴蝶觅食和繁衍行为而衍生出的一种仿生群智能算法,在BOA中每只蝴蝶都会散发出香味,蝴蝶个体能感知香味而互相吸引,香味浓度的计算公式如下:
| $ {f_i} = c{I^a}, $ | (1) |
其中,fi表示蝴蝶个体i感知香味的强度;c表示感知模态参数;I表示蝴蝶散发香味的刺激强度,其值由目标函数值决定;a表示香味吸收程度,a∈[0, 1]。
当蝴蝶能感知到周围有更浓香味时便朝其聚集,此阶段称为全局搜索,其计算公式如下:
| $ x_i^{t + 1} = x_i^t + \left( {{r^2} \times {g^ * } - x_i^t} \right) \times {f_i}。$ | (2) |
当蝴蝶未能感知周围香味时便随机移动,此阶段称为局部搜索,其计算公式如下:
| $ x_i^{t + 1} = x_i^t + \left( {{r^2} \times x_j^t - x_k^t} \right) \times {f_i}。$ | (3) |
式(2)和式(3)中的xit表示蝴蝶个体i在第t代的位置,xjt表示蝴蝶个体j在第t代的位置,xkt表示蝴蝶个体k在第t代的位置,r∈[0, 1],g*表示全局最优解。
2 融合正弦余弦算法的蝴蝶优化算法 2.1 非线性自适应因子大量文献记载了引入自适应权重因子的优势,有线性的,也有非线性的,其主要目的是为了更好地平衡算法的全局搜索和局部搜索能力。这也是算法改进的一个突破口,本文首先在自身认知部分引入非线性自适应因子,使算法迭代初期在较宽范围内搜索,迭代后期在较小范围内搜索。非线性自适应因子的计算公式如下:
| $ \omega \left( t \right) = 2 \times {\rm{exp}}\left( { - {{\left( {4 \times t/Ngen} \right)}^2}} \right), $ | (4) |
其中,exp为指数函数,Ngen为最大迭代次数。
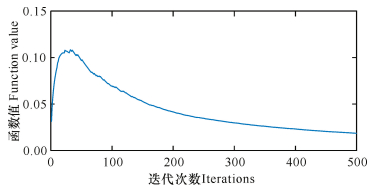
2.2 更改香味浓度计算表达式在BOA中,香味浓度的计算公式如式(1)所示,其值取决于感知模态参数c、香味吸收程度a和蝴蝶散发香味的刺激强度I,其中I值是由目标函数值决定,首先观察Sphere函数香味浓度变化趋势(其他函数变化曲线类似),如图 1所示。
|
| 图 1 香味浓度fi变化曲线 Fig. 1 Variation curve of fi fragrance concentration |
由图 1可知,在迭代过程中香味浓度值变化曲线由小变大再变小,变化的范围较小,不利于全局搜索,而且中后期曲线斜率变化较小导致收敛速度缓慢且计算精度不高。因此用变化范围较宽和斜率变化较大的自适应权重因子重新定义香味浓度计算表达式,其计算公式如下:
| $ b = 2 - 2 \times t/Negen。$ | (5) |
| $ {f_i} = 2 \times b \times r - b, $ | (6) |
b表示随迭代次数变化参数,则蝴蝶全局搜索公式更改为
| $ x_i^{t + 1} = \omega \left( t \right)x_i^t + \left( {{r^2} \times {g^ * } - x_i^t} \right) \times {f_i}。$ | (7) |
正弦余弦算法于2016年由澳大利亚学者Mirjalili[4]提出,该算法利用正余弦函数的周期性和振荡性趋于全局最优,算法中自适应参数能较好地平衡算法的全局搜索和局部开发。计算公式如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;x_i^{t + 1} = \\ \left\{ \begin{array}{l} x_i^t + {r_1} \times \sin \left( {{r_2}} \right) \times \left| {{r_3}{g^ * } - x_i^t} \right|{r_4} < 0.5\\ x_i^t + {r_1} \times \cos \left( {{r_2}} \right) \times \left| {{r_3}{g^ * } - x_i^t} \right|{r_4} \ge 0.5 \end{array} \right., \end{array} $ | (8) |
其中,r1等于式(5),r2∈[0, 2π]之间的随机数,r3, r4∈[0, 1]之间的随机数。
高文欣等[10]和宁杰琼等[12]也使用正弦余弦算法来改进BOA,高文欣等[10]在算法迭代后期让所有蝴蝶个体执行正弦余弦算法,本质上实行算法的串联操作,但在一定程度上增加了算法的时间开销;宁杰琼等[12]在局部搜索过程中以一定概率将正弦余弦算法与基本BOA的局部搜索公式共同寻优。而本文的操作方式与其不同,首先使用非线性自适应因子式(4)替换式(8)中r1,然后用正弦余弦算法替换基本BOA的局部搜索公式,更好地平衡正弦余弦算法的全局搜索和局部勘探能力。因此改进后的正弦余弦算法公式如下:
| $ \begin{array}{l} \;\;\;\;\;\;\;x_i^{t + 1} = \\ \left\{ \begin{array}{l} x_i^t + \omega \left( t \right) \times \sin \left( {{r_2}} \right) \times \left| {{r_3}{g^ * } - x_i^t} \right|{r_4} < 0.5\\ x_i^t + \omega \left( t \right) \times \cos \left( {{r_2}} \right) \times \left| {{r_3}{g^ * } - x_i^t} \right|{r_4} \ge 0.5 \end{array} \right.。\end{array} $ | (9) |
输入:种群规模n、函数名称和最大迭代次数。
① 在边界范围内随机产生种群,并计算此时最优解和最优值
② While t < Ngen
③ 计算式(4)和式(5)
④ For i=1:n
⑤ 计算式(6)
⑥ If i ≤n/2
⑦ 执行式(7)
⑧ Else
⑨ For j=1:dim
⑩ 执行式(9)
⑪ End
⑫ End if
⑬ 越界处理
⑭ 计算蝴蝶个体目标值并与之前个体进行比较,如果优越则替换
⑮ End for
⑯ End While
输出:最优值和最优解
3 仿真实验与结果为检验SCABOA的性能,选取19个基准函数进行测试,函数的具体表达式、维度、取值范围和理论值最优值如表 1所示。实验环境为Matlab2016a和Windows10,机器主频为2.60 GHz,内存为8 GB。
| 函数 Function |
维度 Dim |
范围 Range |
最优值 Optimal value |
| Sphere: |
30 | [-100, 100] | 0 |
| Schwefel 2.22: |
10 | [-10, 10] | 0 |
| Schwefel 1.2: |
10 | [-100, 100] | 0 |
| Schwefel 2.21: |
10 | [-100, 100] | 0 |
| Rosenbrock: |
10 | [-30, 30] | 0 |
| Step: |
10 | [-100, 100] | 0 |
| Quartic: |
10 | [-1.28, 1.28] | 0 |
| Schwefel: |
10 | [-500, 500] | -418.983×n |
| Rastrigin: |
10 | [-5.12, 5.12] | 0 |
| Ackley: |
10 | [-32, 32] | 0 |
| Griewank: |
10 | [-600, 600] | 0 |
| Penalized: |
10 | [-50, 50] | 0 |
| Penalized2: |
10 | [-50, 50] | 0 |
| Foxholes: |
2 | [-65, 65] | 1 |
| Kowalik: |
4 | [-5, 5] | 0.000 3 |
| Six-Hump Camel: |
2 | [-5, 5] | -1.031 6 |
| Branin: |
2 | [-2, 2] | 3 |
| Hartman 3: |
3 | [0, 1] | -3.86 |
| Hartman 6: |
4 | [0, 10] | -10.153 2 |
利用SCABOA对19个基准函数进行求解,并与基本BOA、SCA、SSA、GWO和CS算法进行对比,以验证SCABOA的效果。参数设置:种群规模为30,最大迭代次数为500,其余参数设置与原论文相同。为避免偶然性,每种算法在Matlab2016a软件中独立运行30次,计算每个函数的平均值Mean和方差Std,结果如表 2所示,表中“-”表示文献未对相关函数进行测试,表中的加粗字体为所有实验中的最佳结果。
| f | 指标Index | SCABOA | BOA | SCA | SSA | GWO | CS | SIBOA |
| f1(x) | Mean | 0 | 1.3156e-11 | 12.606 0 | 1.8770e-07 | 1.0907e-27 | 10.802 3 | 1.28e-166 |
| Std | 0 | 7.5462e-13 | 29.551 1 | 2.5680e-07 | 1.3910e-27 | 5.400 1 | 0 | |
| f2(x) | Mean | 0 | 4.7102e-09 | 9.9743e-10 | 0.045 4 | 6.5593e-33 | 0.004 7 | 8.80e-77 |
| Std | 0 | 6.2189e-10 | 2.1436e-09 | 0.127 1 | 1.4601e-32 | 0.001 8 | 3.68e-76 | |
| f3(x) | Mean | 0 | 1.0717e-11 | 0.005 7 | 3.7527e-07 | 1.1882e-25 | 0.050 9 | 5.51e-162 |
| Std | 0 | 1.3529e-12 | 0.015 5 | 1.3493e-06 | 3.3894e-25 | 0.040 6 | 0 | |
| f4(x) | Mean | 0 | 5.2398e-09 | 0.001 2 | 2.3093e-05 | 2.9657e-18 | 0.117 4 | 7.96e-79 |
| Std | 0 | 5.1966e-10 | 0.002 5 | 9.6970e-06 | 4.1874e-18 | 0.033 5 | 5.25e-78 | |
| f5(x) | Mean | 1.3943e-16 | 8.935 6 | 12.789 9 | 131.882 2 | 6.746 3 | 6.072 5 | — |
| Std | 2.9236e-16 | 0.022 7 | 29.204 1 | 364.401 3 | 0.672 6 | 2.136 5 | — | |
| f6(x) | Mean | 4.2398e-19 | 1.206 7 | 0.454 8 | 9.5161e-10 | 0.008 1 | 1.0815e-05 | — |
| Std | 1.0047e-18 | 0.331 9 | 0.180 6 | 3.6020e-10 | 0.044 4 | 5.5343e-06 | — | |
| f7(x) | Mean | 1.1994e-04 | 0.001 6 | 0.002 8 | 0.013 1 | 6.7062e-04 | 0.012 0 | 2.93e-5 |
| Std | 1.1309e-04 | 6.1730e-04 | 0.003 0 | 0.008 0 | 4.4036e-04 | 0.005 2 | 3.52e-5 | |
| f8(x) | Mean | -4.1898e+03 | -2.1109e+03 | -2.1777e+03 | -2.7982e+03 | -2.6908e+03 | -3.4475e+03 | — |
| Std | 3.7002e-12 | 192.375 7 | 147.098 6 | 305.023 1 | 390.166 8 | 141.142 2 | — | |
| f9(x) | Mean | 0 | 32.432 5 | 0.032 8 | 15.786 7 | 0.170 0 | 12.632 1 | 0 |
| Std | 0 | 16.051 6 | 0.134 4 | 6.137 4 | 0.542 7 | 2.703 2 | 0 | |
| f10(x) | Mean | 8.8818e-16 | 2.4744e-09 | 2.4526e-06 | 0.652 7 | 7.0462e-15 | 0.602 5 | 8.8818e-16 |
| Std | 2.0059e-31 | 1.0478e-09 | 5.6780e-06 | 0.946 5 | 1.5979e-15 | 0.521 0 | 2.0059e-31 | |
| f11(x) | Mean | 0 | 1.5542e-13 | 0.069 4 | 0.215 3 | 0.020 4 | 0.080 6 | 0 |
| Std | 0 | 8.7604e-14 | 0.125 2 | 0.112 7 | 0.016 8 | 0.018 7 | 0 | |
| f12(x) | Mean | 4.2735e-19 | 0.109 7 | 0.115 8 | 1.418 1 | 0.004 6 | 0.009 5 | — |
| Std | 7.9882e-19 | 0.068 0 | 0.049 7 | 1.296 1 | 0.008 5 | 0.011 1 | — | |
| f13(x) | Mean | 1.1956e-18 | 0.453 1 | 0.348 4 | 0.003 6 | 0.027 6 | 2.0490e-04 | — |
| Std | 1.6505e-18 | 0.170 2 | 0.080 3 | 0.005 9 | 0.044 1 | 1.7105e-04 | — | |
| f14(x) | Mean | 0.998 0 | 1.343 6 | 1.861 3 | 1.163 4 | 4.815 4 | 0.998 0 | — |
| Std | 6.7752e-16 | 0.588 3 | 0.997 0 | 0.526 6 | 4.343 6 | 6.7752e-16 | — | |
| f15(x) | Mean | 4.0633e-04 | 3.8517e-04 | 9.4201e-04 | 0.002 2 | 0.004 4 | 4.2505e-04 | — |
| Std | 1.0742e-04 | 5.5869e-05 | 3.6319e-04 | 0.005 0 | 0.008 1 | 8.9601e-05 | — | |
| f16(x) | Mean | -1.031 4 | -1.031 5 | -1.031 6 | -1.031 6 | -1.031 6 | -1.031 6 | — |
| Std | 3.7443e-04 | 1.4595e-04 | 4.1014e-05 | 0 | 3.4575e-08 | 0 | — | |
| f17(x) | Mean | 3.260 3 | 3.113 4 | 3.000 0 | 3 | 3.000 0 | 3 | — |
| Std | 2.224 9 | 0.178 3 | 2.9964e-05 | 0 | 3.8635e-05 | 0 | — | |
| f18(x) | Mean | -3.769 3 | -3.838 0 | -3.856 0 | -3.862 8 | -3.861 4 | -3.862 8 | — |
| Std | 0.081 6 | 0.027 7 | 0.003 4 | 1.3550e-15 | 0.002 0 | 1.3550e-15 | — | |
| f19(x) | Mean | -10.153 2 | -5.354 4 | -2.411 4 | -6.731 9 | -9.477 9 | -10.153 2 | — |
| Std | 1.8067e-15 | 0.914 5 | 1.948 9 | 3.564 3 | 1.746 8 | 7.6489e-07 | — |
由表 2第3-8列可知,SCABOA求解的19个基准函数测试中,有8个函数(f1-f4、f8、f9、f11和f19)的平均计算结果达到理论最优值,完全胜出BOA、SCA、SSA、GWO和CS算法。未达到理论最优值的11个函数中,有4个函数f15-f18比BOA、SCA、SSA、GWO和CS算法的平均计算结果稍差且差别较小以外, 另外7个函数的平均计算结果精度高出比较算法十几个数量级。尤其值得一提的是Rosenbrock函数,该函数理论最优值位于一个平滑、狭长的抛物线形山谷中,由于函数为优化算法提供的信息非常有限,使得众多算法求解其最优值变得十分困难,如BOA、SCA、SSA、GWO和CS算法求解的平均值从个位数到百位数不等,而SCABOA算法求解的平均值竟达到1×10-16,与理论最优值更为接近。可见,改进的SCABOA算法计算精度更高。
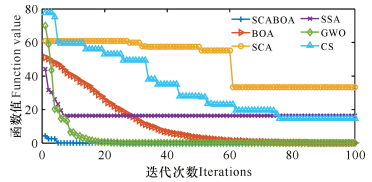
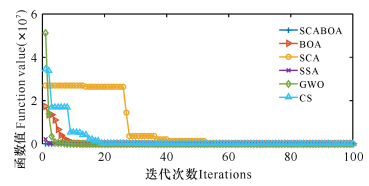
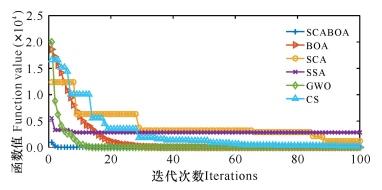
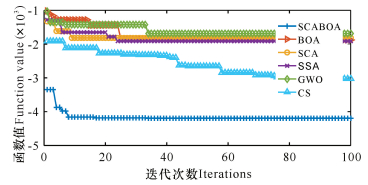
为直观展示SCABOA的收敛速度和寻优精度,给出部分函数前100代的收敛曲线图。从图 2-7可知,SCABOA收敛曲线位于图形最下方,收敛速度最快, 且计算精度最高。
|
| 图 2 f4函数收敛曲线 Fig. 2 Convergence curve of f4 function |
|
| 图 3 f5函数收敛曲线 Fig. 3 Convergence curve of f5 function |
|
| 图 4 f6函数收敛曲线 Fig. 4 Convergence curve of f6 function |
|
| 图 5 f8函数收敛曲线 Fig. 5 Convergence curve of f8 function |
|
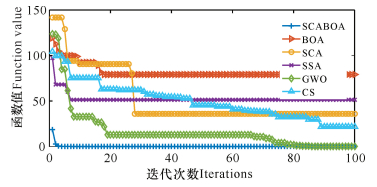
| 图 6 f9函数收敛曲线 Fig. 6 Convergence curve of f9 function |
|
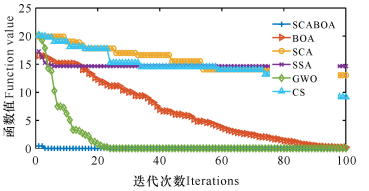
| 图 7 f10函数收敛曲线 Fig. 7 Convergence curve of f10 function |
与高文欣等[10, 14]的改进蝴蝶优化算法进行比较,其测试函数部分与本文相同,求解结果相同部分未列出(具体数据可参考文献),挑选求解结果不同的函数进行比较。如高文欣等[10]的f4即本文中的f12,高文欣等[10]求解的平均值精度仅为10-7,而本文算法求解的平均精度高达10-19,高出12个数量级; 如高文欣等[14]使用的f2即本文中的f2,高文欣等[14]求解的平均值精度仅为1.36e-81,而本文算法求解的平均精度达到理论值。再与王依柔等[11]的算法(SIBOA)进行比较,由于本文中19个测试函数全部包含王依柔等[11]使用的测试函数,故将其结果列于表 2,王依柔等[11]使用的种群规模为40,最大迭代次数为1 000。比较结果:函数f9-f11的计算结果相同,f7的计算结果略次于王依柔等[11],函数f1-f4均优于王依柔等[11];本文算法在种群规模为30和最大迭代次数为500的情况下,总体效果依然优于王依柔等[11]的算法,可见本文算法的优越性。
4 结束语本文在BOA基础之上引入非线性自适应因子、重新定义香味浓度计算公式,嵌入正弦余弦算法,提出一种融合正弦余弦算法的改进蝴蝶优化算法(SCABOA)。比较实验结果可知,SCABOA算法性能表现优越,这与文章第2部分的改进策略分析相吻合:①通过在自身认知部分引入非线性自适应因子,使得算法迭代初期在较宽范围内搜索,而迭代后期在较窄范围搜索;②设计变化范围较宽和斜率变化较大的香味浓度计算公式;③在后半个种群中利用正弦余弦算法替换基本BOA的随机搜索,使得算法搜索更具有目标性。这3种策略的合力结果使得SCABOA算法具有更好的全局搜索和局部搜索能力。
| [1] |
YANG X S, DEB S.Cuckoo search via levy flights[C].Proceedings of World Congress on Nature & Biologically Inspired Computing (NaBIC2009).India: IEEE Publications, 2009: 210-214.
|
| [2] |
MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp swarm algorithm:A bio-inspired optimizer for engineering design problems[J]. Advances in Engineering Software, 2017, 114: 163-191. DOI:10.1016/j.advengsoft.2017.07.002 |
| [3] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007 |
| [4] |
MIRJALILI S. A sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133. DOI:10.1016/j.knosys.2015.12.022 |
| [5] |
MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 |
| [6] |
YANG X S.Flower pollination algorithm for global optimization[C].Unconventional Computation and Natural Computation (UCNC) 2012, Lecture Notes in Computer Science.Berlin: Springer, 2012, 7445: 240-249.
|
| [7] |
王依柔, 张达敏, 徐航, 等. 基于自适应扰动的疯狂蝴蝶算法[J]. 计算机应用研究, 2020, 37(11): 3276-3280. |
| [8] |
SHARMA S, SAHA A K, MAJUMDER A, et al. MPBOA-A novel hybrid butterfly optimization algorithm with symbiosis organisms search for global optimization and image segmentation[J]. Multimedia Tools and Applications, 2021, 80(8): 12035-12076. DOI:10.1007/s11042-020-10053-x |
| [9] |
PROVAS K R, BARUN M, SUBHAM K. Renewable energy-based economic load dispatch using two-step biogeography-based optimization and butterfly optimization algorithm[J]. International Journal of Swarm Intelligence Research, 2020, 11(4): 24-60. DOI:10.4018/IJSIR.2020100102 |
| [10] |
高文欣, 刘升, 肖子雅, 等. 全局优化的蝴蝶优化算法[J]. 计算机应用研究, 2020, 37(10): 2966-2970. |
| [11] |
王依柔, 张达敏, 徐航, 等. 基于自适应扰动的疯狂蝴蝶算法[J]. 计算机应用研究, 2020, 37(11): 3276-3280. |
| [12] |
宁杰琼, 何庆.混合策略改进的蝴蝶优化算法[J/OL].计算机应用研, 2020, 38(5).[2020-12-17].https://www.arocmag.com/article/02-2021-05-017.html.
|
| [13] |
高文欣, 刘升, 肖子雅, 等. 柯西变异和自适应权重优化的蝴蝶算法[J]. 计算机工程与应用, 2020, 56(15): 43-50. DOI:10.3778/j.issn.1002-8331.1907-0048 |
| [14] |
高文欣, 刘升, 肖子雅. 收敛因子和黄金正弦指引机制的蝴蝶优化算法[J]. 计算机工程与设计, 2020, 41(12): 3384-3389. |
| [15] |
谢聪, 封宇. 一种改进的蝴蝶优化算法[J]. 数学的实践与认识, 2020, 50(13): 105-114. |



