2. 中国科学院南海海洋研究所, 中国科学院热带海洋生物资源与生态重点实验室, 广东广州 510301
2. CAS Key Laboratory of Tropical Marine Bio-resources and Ecology, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou, Guangdong, 510301, China
分子动力学起源于1950年左右,其核心是运用牛顿(经典)力学模拟分子体系的运动,并从达到平衡的体系中抽取样本,从统计学的角度计算体系的热力学特征和其他宏观性质[1, 2]。2013年诺贝尔化学奖授予3位美国科学家:Martin Karplus、Michael Levitt和Arieh Warshel教授,以表彰他们发明的分子模拟方法对复杂生命科学领域发展的贡献[3]。这是继1998年诺贝尔化学奖颁给属于理论计算的量子化学后,第二次将诺贝尔化学奖颁给理论计算,同时也标志着分子模拟方法得到实验科学的认可。
分子动力学中最重要的是分子的力场(Force Field,FF),它是计算分子各种性质的基础,直接影响计算结果的可靠性及准确性。根据量子力学波恩-奥本海默近似,忽略电子的运动,可将分子体系的能量视为原子核位置的函数。与量子力学的从头计算方法相比,分子动力学的计算量要小得多,因此能够处理的计算体系也大得多;另一方面,在适当的范围内,基于分子力场的计算精度与量子化学计算相差无几。因此,对大分子复杂体系而言(如蛋白-小分子复合物),基于分子力场的计算是一套经济高效的计算方法。
众所周知,药物研发是一个耗资巨大且周期漫长的高风险过程。据估算,一个药物成功上市需要约10年时间,花费高达14亿美元[4, 5]。近几十年来,随着分子生物学、结构生物学等学科的迅猛发展和高性能计算技术(软件、硬件)的突飞猛进,分子动力学的MM/PB(GB)SA计算方法在先导化合物的筛选环节中得到广泛应用[6]。MM/PB(GB)SA计算是利用分子动力学(Molecular Mechanism)并通过泊松-玻尔兹曼(Poisson Boltzmann)或广义波恩(Generalized Born)模型及分子表面积(Surface Area)的方法,近似求解静电力(ELE)和范德华力(VDW)的贡献。在蛋白-小分子复合物结合自由能的计算过程中,蛋白-小分子复合物的静电力(ELE)和范德华力(VDW)的准确评估是计算的关键,其计算的具体步骤的相关综述已非常全面详细,在此不再累述[7, 8]。
然而,鉴于MM/PB(GB)SA计算方法的局限性(动力学采样、构型的熵变及介电常数选择等)[6],其计算精度及稳定性无法满足药物研发, 尤其是药物结构优化的高精度需求。例如:Sun等[9]系统研究1 508个蛋白-小分子复合物结构熵对MM/PB(GB)SA的影响,与实验值相比,MM/PB(GB)SA计算的绝对结合自由能的平均偏差高达14.7 kcal/mol;Wang等[10]基于165个蛋白-小分子复合物的测试集计算,发现MM/PB(GB)SA计算与实验值的平均绝对值偏差为9.7 kcal/mol。与之相反,结合自由能微扰积分法通过构建热力学循环,可对蛋白-小分子复合物的结合自由能进行精确计算,越来越受到人们的重视。例如,He等[11]利用结合自由能微扰积分法计算134个蛋白-小分子复合物的结合自由能,其平均绝对误差仅为0.71—0.94 kcal/mol,该精度可为先导化合物的结构优化提供非常重要的指导。本文首先介绍以分子动力学为基础的结合自由能微扰积分法的计算过程,然后介绍限制势的引入方法,最后通过具体的计算案例展现结合自由能微扰积分法计算在药物研发中的应用前景。
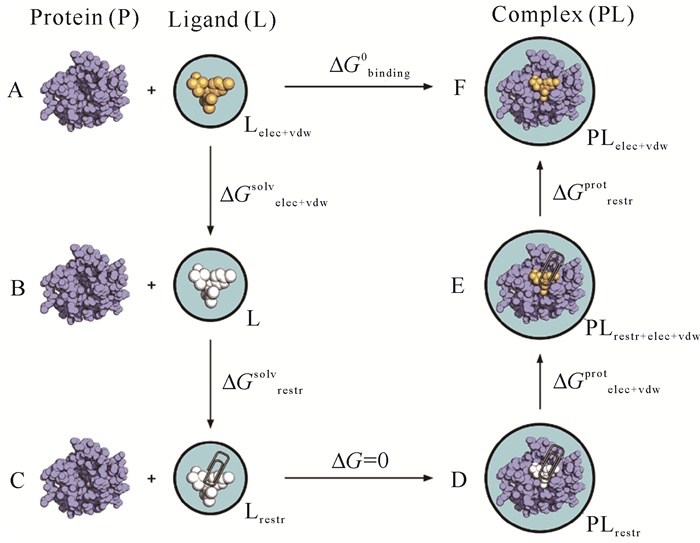
1 结合自由能微扰积分法的计算过程 1.1 构建炼金术热力学循环动力学模拟不是直接模拟实验中小分子与蛋白相结合的真实过程,而是通过建立热力学循环间接计算小分子与靶蛋白的结合自由能(ΔGbinding0)[12-14]。如图 1所示,在状态A下,假设蛋白与小分子远离,此时小分子与蛋白之间还没有相互作用,而小分子与环境(如溶剂水)间具有相互作用(橙色表示有相互作用),该相互作用此时包含小分子-溶剂两者间的静电力(ELE)和范德华力(VDW);状态B:分别慢慢关闭小分子与环境间的相互作用,即小分子-溶剂间的ELE和VDW,此时的小分子如同虚原子(Ghost Atoms,白色表示小分子此时与环境无相互作用);状态C:无相互作用力的小分子与蛋白结合,进入蛋白的结合口袋,形成状态D中的复合物,图中回形针表示为将小分子限制在蛋白口袋中所引入的限制势;状态E:小分子在蛋白的结合口袋中,慢慢打开小分子与靶蛋白间的ELE和VDW;状态F:移除小分子与蛋白间的限制势,形成闭合的热力学循环。因此,由A直接到F变化的结合自由能ΔGbinding0,可等价于由状态A经状态B—E转变为状态F过程的能量变化总和。
通过分别模拟小分子在溶剂水和靶蛋白的口袋中,慢慢关闭或打开小分子与环境间的相互作用(ELE和VDW),以上两个过程构成了一个热力学循环。由于小分子与环境间相互作用的关闭(或打开)的过程是不存在的非真实物理过程,因此该计算过程也被称为“炼金术”。
1.2 结合自由能微扰积分过程结合自由能微扰积分法,最早是由Kirkwood等[15]于1935年提出的。该方法通过向哈密顿量H(p, q)中引入一个耦合参数λ,再对λ进行积分计算出该过程的自由能变化,其中p和q分别代表离粒子的动量和原子位置。以图 1状态A到B的过程中ELE变化为例,如果λ=1表示小分子处于状态A,即小分子与环境具有完全的静电力作用;λ=0代表状态B,此时小分子与环境没有静电力作用,那么此过程中静电力作用的能量变化为
| $ \mathit{\Delta} G=\int_{0}^{1}\left\langle\frac{\partial H(p, q, \lambda)}{\partial \lambda}\right\rangle_{\lambda} \mathrm{d} \lambda。$ |
在实际计算过程中,λ是从0到1间一系列连续的取值。每一个λ值,也被称为一个窗口。首先创建一系列的λ点(或窗口),分别计算每个窗口蛋白-小分子复合物的结合自由能;然后通过积分,求得此过程的自由能变化。如果λ的值越多(窗口越密集),计算误差将越小,但总体计算的耗时也将相应延长。一般来说,λ值的分布可采取等间距的办法,如Aldeghi等[12]采用等间距dλ=0.1和0.05分别计算ELE和VDW的贡献;λ值的分布也可以选择非等间隔值,如He等[11]比较不同λ取值对计算的影响,并利用高斯求积法提出一个仅含9个λ的经济计算策略。类似地,将静电力换成范德华力时,也可求得状态A到状态B过程中范德华力的贡献。最后,通过上述热力学循环,小分子与蛋白的结合自由能(ΔGbinding0)可等价于从状态A经状态B—E等到达状态F过程的自由能变化总和。
1.3 自由能计算精度的关键:动力学采样动力学模拟过程中的采样是影响计算精度的一个关键因素[16, 17]。以蛋白-小分子复合物为例,实验上观察到小分子进入蛋白结合口袋后,与蛋白稳定地结合在一起,其变化过程属于自发行为。在能量上,其变化过程的吉布斯自由能为负值,根据范特霍夫等温公式:
| $ \mathit{\Delta} G=-R T \ln K, $ |
其中R、T和K分别为气体常数、反应的温度和反应平衡常数。K代表了小分子与蛋白结合、解离两种状态间的动态平衡。
在实际的模拟过程中,由于逐渐关闭了小分子与蛋白及环境间的相互作用力(ELE和VDW),此时蛋白与小分子复合物倾向于非结合状态。如果要对蛋白-小分子的结合状态有足够的采样,往往需要非常长的模拟时间。因此,为增强蛋白-小分子结合状态时的模拟采样,在实际计算过程中可通过人为引入限制势来实现,即引入一个合理大小的作用力,约束蛋白-小分子复合物保持结合状态。首先对蛋白与小分子复合物进行常温常压下(NPT)的常规动力学模拟,并对其平衡状态进行一段时间的采样(如10 ns),评估蛋白-小分子复合物在平衡位置附近正常的波动范围,然后分别从蛋白(P)和小分子(L)中分别选择3个重原子(除氢原子以外的原子)作为参考原子建立限制势。
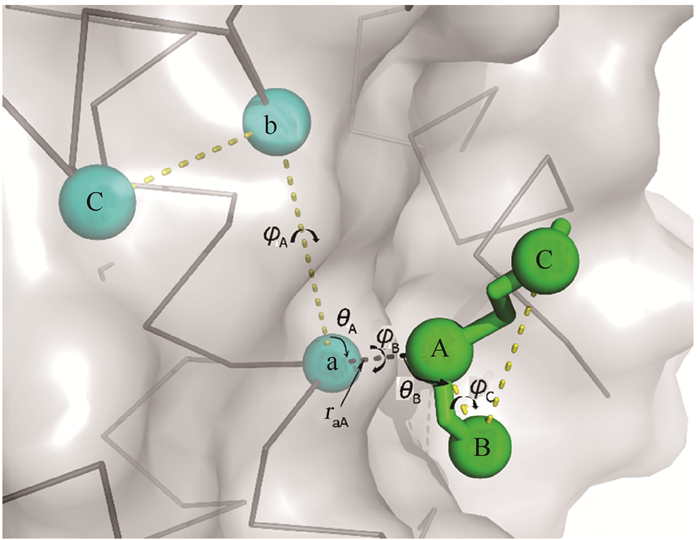
如果原子允许的波动越小,则限制势越强,对应地对复合物解离时的采样时间越长,反之亦然。因此,在实际处理中仅考虑50%的原子的波动,试图选取一个平衡点。首先,分别计算蛋白及小分子各重原子在平衡状态中的正常波动(RMSF),并按升序排列,选取前50%波动较小的原子建立参考列表。以小分子的3个参考原子选取为例,选择RMSF最小的重原子为第一个原子LA,参考列表中距离LA最远的原子为LB,参考列表中距离前两个原子最远的重原子为第三个参考原子LC。这样做是确保对于柔性较大的分子,其质心也能保持稳定。与此类似地,从蛋白结构中选择3个参考原子Pa、Pb和Pc(图 2)。限制势则包含1个键长raA(即原子Pa和LA间的键长)、2个键角(θA、θB分别表示Pb-Pa-LA和Pa-LA-LB的键角)和3个二面角(φA、φB、φC分别表示二面角Pc-Pb-Pa-LA、Pb-Pa-LA-LB和Pa-LA-LB-LC)。
|
| 图 2 蛋白(P,灰色)-小分子(L,绿色)复合物限制势中参考原子的示意图 Fig. 2 Schematic diagram of the reference atom in the confinement potential of protein (P, gray) and ligand(L, green) complexes |
随后,假定限制势使得原子在平衡位置做简谐振动。以两个参考原子Pa和LA间键长(raA)为例,即简谐势U(x)=kr(x-x0)2,其中x表示任意一次采样的键长raA,x0为两个参考原子的平均平衡键长。那么简谐常数kr为
| $ k_{r}=0.6 /(2 \sigma)_{r}^{2}, $ |
其中,2σ表示上述采样过程中,raA在室温(T=298 K,其势能为1 kT,k为玻尔兹曼常数,即0.6 kcal/mol)下的正常波动范围,从而可以求得键长的简谐常数kr。依此类推,同样可以求得其他参考原子间的键角、二面角间的简谐常数(kθA、kθB、kφA、kφB、kφC),从而可求得其限制势(ΔF)大小[18, 19]:
| $ \mathit{\Delta} F=-k T\left[\frac{8 \pi^{2} V\left(k_{r_{a \mathrm{~A}}} k_{\theta_{\mathrm{A}}} k_{\theta_{\mathrm{B}}} k_{\varphi_{\mathrm{A}}} k_{\varphi_{\mathrm{B}}} k_{\varphi_{\mathrm{C}}}\right)^{\frac{1}{2}}}{r_{\text {aA. } 0}^{2} \sin \theta_{\text {A. } 0} \sin \theta_{\text {B. } 0}(2 \pi k T)^{3}}\right], $ |
其中,k、T、V分别是玻尔兹曼常数、体系所处温度和模拟体系的体积;raA.0、sinθA.0和sinθB.0分别是键长和键角处于平衡态时的平均值。
需要说明的是,增强动力学采样是提高结合自由能计算精度的一个有效手段,但不是唯一方法。例如,Laury等[19]通过对葫芦脲及14个不同大小化合物的结合自由能计算发现,使用可极化的分子力场也可以提高结合自由能微扰积分法的计算精度。
2 结合自由能微扰积分法在药物研发中的应用 2.1 先导化合物结构的优化先导化合物的结构优化是药物能否进入临床研究的关键。高精度的结合自由能微扰积分法可为先导化合物的结构优化提供重要的指导,加速药物的研发进程。基于前述范特霍夫等温公式可知,当蛋白-小分子复合物结合自由能相差0.6 kcal/mol时,蛋白-小分子复合物的反应平衡常数相差10倍。因此,高精度的结合自由能计算对精细地区分不同取代基的小分子与靶蛋白结合活性差异至关重要。表 1选取了2015年以来结合自由能微扰积分法的一些代表性研究。当前主要关注结合自由能微扰积分法在计算案例中的计算精度,而总体上说,结合自由能微扰积分法的精度已经达到或接近于化学精度(1 kcal/mol)。如2015年,Wang等[20]针对8个靶蛋白系统地测试199个小分子的结合自由能,理论计算结果与实验值的相关性达到0.75,且实验误差仅1.1 kcal/mol。该研究工作首次构建了1个高质量的训练集,并含有多个靶蛋白及结构多样的小分子化合物,为后续相关计算方法的研究提供了测试基础与便利。另外,该研究也系统地评估分子对接(Glide标准精度模式)、基于动力学的广义玻恩模型(MM/GBSA)计算,以及结合自由能微扰积分法计算的稳定性和计算精度。与分子对接及MM/GBSA相比(分子对接和MM/GBSA计算结果与实验的相关性分别为0.29和0.35),结合自由能微扰积分法不仅精度高(0.75),而且计算的鲁棒性得以证实。Steinbrecher等[21]利用结合自由能微扰积分法计算实现对小分子碎片的活性预测,从而有利于早期先导药物母核结构的开发。Aldeghi等[12]及Ciordia等[22]分别测试了蛋白-小分子复合物的结合自由能,其结果与实验值误差最小时仅差0.60和0.57 kcal/mol。Lenselink等[23]则将结合自由能的计算成功应用到G蛋白偶联受体(GPCR)的药物开发中,并获得非常高的计算精度(均方根偏移RMSD仅为0.58—1.56),为深入了解GPCR的结构和功能奠定了重要的理论基础。Araki等[24]基于激酶蛋白构型的柔性,计算靶向周期蛋白依赖激酶2(CDK2)和细胞外调节蛋白激酶2(ERK2)的小分子抑制剂的结合自由能,并获得非常好的相关性(R=0.81)。Li等[25]开发出一种基于高斯法则的结合自由能微扰积分法,对训练集的计算表明其结合自由能变化与实验活性的相关性R值达到0.69—0.94,并将该计算方法应用于靶向phosphodiesterase-10蛋白的苗头化合物优化,最终得到优化后的化合物,并将其活性提高近2 000倍。
| 年份 Year |
靶蛋白 Target protein |
小分子数目 Number of ligands |
相关性 Corrlation |
与实验的均方根差 RMSD (kcal/mol) |
参考文献 Reference |
| 2015 | BACE, CDK2, JNK1, etc | 199 | 0.75 | 1.10 | [20] |
| 2015 | Lysozyme, DNA Ligase, MCL1, etc | 96 | 0.81 | 1.14 | [21] |
| 2016 | BRD4 | 11 | 0.84 | 0.60 | [12] |
| 2016 | BACE1 | 50 | 0.67—0.83 | 0.57—1.04 | [22] |
| 2016 | GPCR | 45 | 0.62 | 0.58—1.56 | [23] |
| 2016 | CDK2,ERK2 | 24 | 0.81 | 2—3 | [24] |
| 2017 | CDK2, PTP1B, MCL1, etc | 55 | 0.80—0.90 | 0.80—1.40 | [26] |
| 2017 | BRDs BRD2 |
2 1 |
0.75 0.48 |
0.81 1.76 |
[27] |
| 2018 | AChE | 8 | 0.79 | — | [28] |
| 2018 | PDZ | 18 peptides | — | 1.2 | [29] |
| 2018 | Galectin-3 | 8 | 0.7—0.9 | 0.48—0.72 | [30] |
| 2019 | CDK2, JNK1, TYK2, etc | 101 | 0.69—0.94 | 0.62—1.54 | [25] |
| 2019 | Lysozyme, AKT1, THR, etc | 36 | 0.8—0.98 | 0.57—1.86 | [31] |
| 2019 | Thrombin | 10 | — | < 1.0 | [32] |
| 2020 | Lysozyme, CAⅡ, SND1, etc | 87 mutation | — | 1.11 | [33] |
| 2020 | BACE, CDK2, MCL1, etc | 134 | 0.48—0.80 | 0.91—1.41 | [11] |
| 2020 | DHQase | 6 | 0.85±0.15 | 4.28±0.69 | [34] |
| 2020 | MDM2 MDMX |
14 5 |
0.43 0.86 |
1.95 0.82 |
[35] |
| 注:“一”表示未进行相关性的比较 Note:"-" means the correlation is not compared | |||||
2.2 蛋白-小分子复合物结合活性预测
结合自由能微扰积分法可对蛋白-小分子复合物结合活性进行理论预测,有利于筛选出最高活性的化合物,从而加速药物研发效率。为此,Bhati等[26]通过考虑系统中的多样本,提出一个提高积分法精度的计算方法,基于含有5个蛋白及55个小分子的测试集的计算结果显示,其与实验值的相关性R达到0.80—0.90。2017年Aldeghi等[27]通过结合自由能计算探讨靶向Bromodomain (BRD)蛋白抑制剂的选择性与活性,发现对化合物活性预测的平均误差为0.81 kcal/mol,且相关性达到0.75;另外,该研究发现优化小分子磺酰胺基团的力场参数可提高计算准确性,也表明分子力场对于计算精度的重要性。Panel等[29]将结合自由能微扰积分法成功地应用到短肽-蛋白结合活性预测中,其计算的平均偏差最小达到0.37 kcal/mol,进一步拓展了结合自由能微扰积分法的应用范围。
需要指出的是,尽管结合自由能微扰积分法展现出了高精度和稳定性,目前绝大部分的计算仍是基于回顾性分析的结果,在实际运用中的预测能力还需进一步观察与评估。例如:Qian等[36]基于不同力场的结合自由能微扰积分法评估巨噬细胞游走抑制因子(Protein Macrophage Migration Inhibitory Factor)与其抑制剂间的结合自由能,计算过程中当小分子采用OPLS-AA/M力场及CM5原子电荷,基于蒙特卡洛或者分子动力学预测的结合自由能与实验结果一致, 分别为(-8.80±0.74)和(-8.46±0.85) kcal/mol,实验值为(-8.98±0.28) kcal/mol;然而,当选用CHARMM和AMBER力场重复上述结合自由能计算时,预测的结合自由能最高误差达6 kcal/mol。另一方面,Loeffler等[37]用结合自由能微扰积分法评估主流分子模拟软件计算小分子与溶剂的溶解自由能(即结合自由能)的异同,发现尽管各软件虽然在力场参数、数学表达式上不同,但对测试集的计算结果在数字上均符合预期,且其差别小于0.2 kcal/mol。以上结果说明,因不同的计算软件和力场参数所导致的结合自由能预测计算误差可能性非常小,6 kcal/mol的预测误差很可能是由于蛋白与小分子的力场参数不匹配、不兼容造成的,另一方面也表明选择匹配的力场参数对于准确计算至关重要。但如何才能选出适合的力场参数,却仍是实际应用过程中的一个难点。尽管Aldeghi等[38]详细介绍了结合自由能计算中的基础方法与流程选择,Abel等[39]提出改善结合自由能计算精度的一些经验与策略,但目前还没有一个统一的计算流程和方法可供不同软件使用,仍需进一步发展与完善。因此,在实际运用中,需要对计算方法与流程、计算参数等进行测试与验证,在此基础上才能准确地预测蛋白-小分子复合物的结合活性。
2.3 脂水分配系数(logP)的计算logP是药物小分子一个非常重要的物理化学性质,对于药物在体内的分布、代谢及吸收等至关重要。利用结合自由能微扰积分法对logP(或logD)的计算[40-44],不仅对药物的物理化学性质预测具有重要的应用价值,同时也有利于计算方法本身的完善。例如,logP计算已成为模拟计算测试(SAMPL)[44]中检验计算方法、力场参数的常规项目。当前,结合自由能微扰积分法对分子量较小的化合物的logP计算已经取得非常高的精度。例如:Garrido等[45]计算不同力场下的烷烃(n=1—8)的logP值,发现利用最优组合的参数条件(OPLS-AA/TraPPE力场)所得出的logP预测值与实验值的平均误差仅0.1个log单位。Bannan等[41]创建了一个含有41个小分子的测试集,并系统计算了该测试集在正辛烷及环己烷环境中的脂水分配系数,结果与实验值的相关性(R)分别为0.70和0.83。
另外,对化合物logP的计算也可以为化合物小分子的结构改造与优化提供理论依据与合理解释。例如,Liu等[46]利用结合自由能微扰积分法计算上市小分子药物TAK-438[47, 48](一个全新的钾离子竞争型酸阻滞剂)不同氟取代位点的logP,发现logP与活性的变化存在良好的线性关系,认为单氟取代通过改变小分子化合物整体的偶极,从而调控化合物logP的变化,并成功地定性解释了小分子抑制剂的不同氟取代点与抑制活性的关系。最后得出结论,单氟取代引起的logP变化是导致该系列化合物抑制活性巨大差异的根本原因。
2.4 蛋白与小分子结合模式的预测蛋白与小分子结合模式是指小分子在靶蛋白的结合口袋中的活性构象及相互作用。一般来说,实验室通过随机生物学普筛或者盲筛,获得少量具有生物活性的苗头化合物;在此基础上,利用X射线单晶衍射(X-ray)、核磁共振技术(NMR)或者冷冻电镜(Cryo-EM)等技术手段解析出苗头化合物与靶蛋白两者间的相互作用模式。靶蛋白与苗头化合物的结合模式是进一步对苗头化合物进行合理地结构优化与修饰的基础。但上述的实验手段一般都具有实验操作苛刻、耗时较长、花费较高等缺点, 因此可以借助结合自由能微扰积分法快速准确地预测出蛋白与小分子的结合模式。鉴于结合自由能微扰积分法的密集型计算需求,可利用分子动力学对蛋白与小分子对接构型进行稳定性分析,快速剔除部分非稳定的对接构型。Liu等[49, 50]从晶体结构数据库中分别选出108和104个高质量的晶体结构作为测试集,并开展两种方式的分子对接:第一种是自我对接,即将晶体结构中的小分子对接回原蛋白[49];第二种是交叉对接,即用同一靶蛋白的不同抑制剂进行交叉对接[50]。针对每一个小分子分别选取3个代表性的对接构型(其中1个与晶体结构最接近的正确构型,2个诱饵构型),通过动力学稳定性分析可剔除35%—55%的诱饵构型,从而大大降低下一步的蛋白-小分子结合活性预测的计算量。同时研究还发现,动力学稳定性分析还能够优化分子对接的构型[49, 50],这一发现最近也被其他课题组所证实[51]。紧接着,Liu等[52]对第二个训练集(共104个晶体结构)里剩余构象进行蛋白-小分子结合活性预测,发现72%(75/104)的复合物结合模式能够被结合自由能微扰积分法正确地识别出。该结果表明利用分子动力学的结合自由能微扰积分法预测蛋白与小分子结合模式是可行的。最近,Zhang等[53]也成功将结合自由能微扰积分法应用于新型冠状病毒(COVID-19)及其抑制剂瑞德西韦(Remdesivir)的结合模式预测的研究中,不仅预测了瑞德西韦可能的结合位点,同时也指出该结合模式下起重要作用的关键氨基酸,为进一步开发出更高活性的抑制剂提供理论指导和依据。另外,Aldeghi等[27]在预测靶向BRD蛋白家族的广谱性小分子抑制剂的结合模式及其抑制活性时,发现预测活性与实验值的误差为1.76 kcal/mol,其相关性仅为0.48。该研究表明当前蛋白-小分子结合模式的预测难点,即分子动力学的结合自由能微扰积分法对蛋白-小分子两者间的精细结构非常敏感,即便是相似的结合模式,不同蛋白-小分子结合活性预测值变化也比较大,因此需要对蛋白与小分子结合模式与活性预测仔细分析验证。
3 展望本文简要介绍了以分子动力学为基础的结合自由能微扰积分法在药物研发中的应用。随着高性能计算机的发展(如基于图形处理器GPU的计算[11]),分子动力学模拟的计算速度也将迎来质的飞跃[54, 55]。另一方面,越来越多高精度的量子化学的计算结果也为分子动力学力场参数的优化提供了高质量的数据来源[56, 57],而力场的不断发展与完善也将为分子动力学的应用注入新的活力。
考虑到结合自由能微扰积分法计算步骤冗长、设置烦琐,目前已有集成化、开源程序可供使用。例如:FEsetup[58]程序可兼容目前主流的动力学模拟软件和程序,方便计算流程的自动化设置与计算,而alchemy-analysis[59]和MBAR[60]等分析工具则可简化后期的数据处理与分析,如检测动力学模拟过程中的采样是否收敛、热力学循环过程中的能量计算及误差分析。这些程序与软件的出现与发展,将大大降低结合自由能微扰积分法的使用门槛。相信随着结合自由能微扰积分法计算的普及,其在药物研发中将发挥更加重要的作用。
| [1] |
FRENKEL D, SMIT B. Understanding molecular simulation:From algorithms to applications[M]. Second edition.San Diego: Academic Press, 2002.
|
| [2] |
陈正隆, 徐为人, 汤立达. 分子模拟的理论与实践[M]. 北京: 化学工业出版社, 2007.
|
| [3] |
The nobel prize in chemistry 2013[EB/OL]. https://www.nobelprize.org/prizes/chemistry/2013/summary/.
|
| [4] |
PAUL S M, MYTELKA D S, DUNWIDDIE C T, et al. How to improve R & D productivity:The pharmaceutical industry's grand challenge[J]. Nature Reviews Drug Discovery, 2010, 9(3): 203-214. DOI:10.1038/nrd3078 |
| [5] |
PRASAD V, MAILANKODY S. Research and development spending to bring a single cancer drug to market and revenues after approval[J]. JAMA Internal Medicine, 2017, 177(11): 1569-1575. DOI:10.1001/jamainternmed.2017.3601 |
| [6] |
WANG E, SUN H, WANG J, et al. End-point binding free energy calculation with MM/PBSA and MM/GBSA:Strategies and applications in drug design[J]. Chemical Reviews, 2019, 119(16): 9478-9508. DOI:10.1021/acs.chemrev.9b00055 |
| [7] |
HOMEYER N, GOHLKE H. Free energy calculations by the molecular mechanics Poisson-Boltzmann surface area method[J]. Molecular Informatics, 2012, 31(2): 114-122. DOI:10.1002/minf.201100135 |
| [8] |
HANSEN N, VAN GUNSTEREN W F. Practical aspects of free-energy calculations:A review[J]. Journal of Chemical Theory and Computation, 2014, 10(7): 2632-2647. DOI:10.1021/ct500161f |
| [9] |
SUN H, DUAN L, CHEN F, et al. Assessing the performance of MM/PBSA and MM/GBSA methods.7.Entropy effects on the performance of end-point binding free energy calculation approaches[J]. Physical Chemistry Chemical Physics, 2018, 20(21): 14450-14460. DOI:10.1039/C7CP07623A |
| [10] |
WANG E, LIU H, WANG J, et al. Development and evaluation of MM/GBSA based on a variable dielectric GB model for predicting protein-ligand binding affinities[J]. Journal of Chemical Information and Modeling, 2020, 60(11): 5353-5365. DOI:10.1021/acs.jcim.0c00024 |
| [11] |
HE X, LIU S, LEE T S, et al. Fast, accurate, and reliable protocols for routine calculations of protein-ligand binding affinities in drug design projects using AMBER GPU-TI with ff14SB/GAFF[J]. ACS Omega, 2020, 5(9): 4611-4619. DOI:10.1021/acsomega.9b04233 |
| [12] |
ALDEGHI M, HEIFETZ A, BODKIN M J, et al. Accurate calculation of the absolute free energy of binding for drug molecules[J]. Chemical Science, 2016, 7(1): 207-218. DOI:10.1039/C5SC02678D |
| [13] |
CHIPOT C, POHORILLE A. Free energy calcula-tions:Theory and applications in chemistry and biology[M]. Berlin: Springer, 2007.
|
| [14] |
WILLIAMS-NOONAN B J, YURIEV E, CHALMERS D K. Free energy methods in drug design:Prospects of "alchemical perturbation" in medicinal chemistry[J]. Journal of Medicinal Chemistry, 2018, 61(3): 638-649. DOI:10.1021/acs.jmedchem.7b00681 |
| [15] |
KIRKWOOD J G. Statistical mechanics of fluid mixtures[J]. The Journal of Chemical Physics, 1935, 3(5): 300-313. DOI:10.1063/1.1749657 |
| [16] |
BERNARDI R C, MELO M C R, SCHULTEN K. Enhanced sampling techniques in molecular dynamics simulations of biological systems[J]. Biochimica et Biophysica Acta:General Subjects, 2015, 1850(5): 872-877. DOI:10.1016/j.bbagen.2014.10.019 |
| [17] |
陈淏川, 付浩浩, 邵学广, 等. 重要性采样方法与自由能计算[J]. 化学进展, 2018, 30(7): 921-931. |
| [18] |
BORESCH S, TETTINGER F, LEITGEB M, et al. Absolute binding free energies:A quantitative approach for their calculation[J]. The Journal of Physical Chemistry B, 2003, 107(35): 9535-9551. DOI:10.1021/jp0217839 |
| [19] |
LAURY M L, WANG Z, GORDON A S, et al. Absolute binding free energies for the SAMPL6 cucurbit[8] uril host-guest challenge via the AMOEBA polarizable force field[J]. Journal of Computer-Aided Molecular Design, 2018, 32(10): 1087-1095. DOI:10.1007/s10822-018-0147-5 |
| [20] |
WANG L, WU Y, DENG Y, et al. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field[J]. Journal of the American Chemical Society, 2015, 137(7): 2695-2703. DOI:10.1021/ja512751q |
| [21] |
STEINBRECHER T B, DAHLGREN M, CAPPEL D, et al. Accurate binding free energy predictions in fragment optimization[J]. Journal of Chemical Information and Modeling, 2015, 55(11): 2411-2420. DOI:10.1021/acs.jcim.5b00538 |
| [22] |
CIORDIA M, PÉREZ-BENITO L, DELGADO F, et al. Application of free energy perturbation for the design of BACE1 inhibitors[J]. Journal of Chemical Information and Modeling, 2016, 56(9): 1856-1871. DOI:10.1021/acs.jcim.6b00220 |
| [23] |
LENSELINK E B, LOUVEL J, FORTI A F, et al. Predicting binding affinities for GPCR ligands using free-energy perturbation[J]. ACS Omega, 2016, 1(2): 293-304. DOI:10.1021/acsomega.6b00086 |
| [24] |
ARAKI M, KAMIYA N, SATO M, et al. The effect of conformational flexibility on binding free energy estimation between kinases and their inhibitors[J]. Journal of Chemical Information and Modeling, 2016, 56(12): 2445-2456. DOI:10.1021/acs.jcim.6b00398 |
| [25] |
LI Z, HUANG Y, WU Y, et al. Absolute binding free energy calculation and design of a subnanomolar inhibitor of phosphodiesterase-10[J]. Journal of Medicinal Chemistry, 2019, 62(4): 2099-2111. DOI:10.1021/acs.jmedchem.8b01763 |
| [26] |
BHATI A P, WAN S, WRIGHT D W, et al. Rapid, accurate, precise, and reliable relative free energy prediction using ensemble based thermodynamic integration[J]. Journal of Chemical Theory and Computation, 2017, 13(1): 210-222. DOI:10.1021/acs.jctc.6b00979 |
| [27] |
ALDEGHI M, HEIFETZ A, BODKIN M J, et al. Predictions of ligand selectivity from absolute binding free energy calculations[J]. Journal of the American Chemical Society, 2017, 139(2): 946-957. DOI:10.1021/jacs.6b11467 |
| [28] |
NASCIMENTO É C M, OLIVA M, ANDRÉS J. Binding free energy calculations to rationalize the interactions of huprines with acetylcholinesterase[J]. Journal of Computer-Aided Molecular Design, 2018, 32(5): 607-622. DOI:10.1007/s10822-018-0114-1 |
| [29] |
PANEL N, VILLA F, FUENTES E J, et al. Accurate PDZ/peptide binding specificity with additive and polarizable free energy simulations[J]. Biophysical Journal, 2018, 114(5): 1091-1102. DOI:10.1016/j.bpj.2018.01.008 |
| [30] |
MANZONI F, RYDE U. Assessing the stability of free-energy perturbation calculations by performing variations in the method[J]. Journal of Computer-Aided Molecular Design, 2018, 32(4): 529-536. DOI:10.1007/s10822-018-0110-5 |
| [31] |
FRATEV F, SIRIMULLA S. An improved free energy perturbation FEP+ sampling protocol for flexible ligand-binding domains[J]. Scientific Reports, 2019, 9(1): 16829. DOI:10.1038/s41598-019-53133-1 |
| [32] |
MONDAL D, FLORIAN J, WARSHEL A. Exploring the effectiveness of binding free energy calculations[J]. The Journal of Physical Chemistry B, 2019, 123(42): 8910-8915. DOI:10.1021/acs.jpcb.9b07593 |
| [33] |
DUAN J, LUPYAN D, WANG L. Improving the accuracy of protein thermostability predictions for single point mutations[J]. Biophysical Journal, 2020, 119(1): 115-127. DOI:10.1016/j.bpj.2020.05.020 |
| [34] |
NGO S T, NGUYEN T H, TUNG N T, et al. Oversampling free energy perturbation simulation in determination of the ligand-binding free energy[J]. Journal of Computational Chemistry, 2020, 41(7): 611-618. DOI:10.1002/jcc.26130 |
| [35] |
SINGH N, LI W. Absolute binding free energy calculations for highly flexible protein MDM2 and its inhibitors[J]. International Journal of Molecular Sciences, 2020, 21(13): 4765. DOI:10.3390/ijms21134765 |
| [36] |
QIAN Y, DE VACA I C, VILSECK J Z, et al. Absolute free energy of binding calculations for macrophage migration inhibitory factor in complex with a druglike inhibitor[J]. The Journal of Physical Chemistry B, 2019, 123(41): 8675-8685. DOI:10.1021/acs.jpcb.9b07588 |
| [37] |
LOEFFLER H H, BOSISIO S, MATOS G D R, et al. Reproducibility of free energy calculations across different molecular simulation software packages[J]. Journal of Chemical Theory and Computation, 2018, 14(11): 5567-5582. DOI:10.1021/acs.jctc.8b00544 |
| [38] |
ALDEGHI M, BLUCK J P, BIGGIN P C. Absolute alchemical free energy calculations for ligand binding:A beginner's guide[J]. Methods in Molecular Biology, 2018, 1762: 199-232. |
| [39] |
ABEL R, WANG L, MOBLEY D L, et al. A critical review of validation, blind testing, and real-world use of alchemical protein-ligand binding free energy calculations[J]. Current Topics in Medicinal Chemistry, 2017, 17(23): 2577-2585. DOI:10.2174/1568026617666170414142131 |
| [40] |
MATOS G D R, KYU D Y, LOEFFLER H H, et al. Approaches for calculating solvation free energies and enthalpies demonstrated with an update of the freesolv database[J]. Journal of Chemical & Engineering Data, 2017, 62(5): 1559-1569. |
| [41] |
BANNAN C C, CALABRÓ G, KYU D Y, et al. Calculating partition coefficients of small molecules in octanol/water and cyclohexane/water[J]. Journal of Chemical Theory and Computation, 2016, 12(8): 4015-4024. DOI:10.1021/acs.jctc.6b00449 |
| [42] |
BHATNAGAR N, KAMATH G, CHELST I, et al. Direct calculation of 1-octanol-water partition coefficients from adaptive biasing force molecular dynamics simulations[J]. The Journal of Chemical Physics, 2012, 137(1): 014502. DOI:10.1063/1.4730040 |
| [43] |
KLIMOVICH P V, MOBLEY D L. Predicting hydration free energies using all-atom molecular dynamics simulations and multiple starting conformations[J]. Journal of Computer-Aided Molecular Design, 2010, 24(4): 307-316. DOI:10.1007/s10822-010-9343-7 |
| [44] |
GUTHRIE J P. A blind challenge for computational solvation free energies:Introduction and overview[J]. The Journal of Physical Chemistry B, 2009, 113(14): 4501-4507. DOI:10.1021/jp806724u |
| [45] |
GARRIDO N M, QUEIMADA A J, JORGE M, et al. 1-octanol/water partition coefficients of n-alkanes from molecular simulations of absolute solvation free energies[J]. Journal of Chemical Theory and Computation, 2009, 5(9): 2436-2446. DOI:10.1021/ct900214y |
| [46] |
LIU K, KOKUBO H. Uncovering abnormal changes in logP after fluorination using molecular dynamics simulations[J]. Journal of Computer-Aided Molecular Design, 2019, 33(3): 345-356. DOI:10.1007/s10822-018-0183-1 |
| [47] |
赵世峰, 汪荣华. 新型抑酸药物钾离子竞争型酸阻滞剂研发进展[J]. 中国临床药理学与治疗学, 2018, 23(3): 352-360. |
| [48] |
ARIKAWA Y, NISHIDA H, KURASAWA O, et al. Discovery of a novel pyrrole derivative 1-[5-(2-fluorophenyl)-1-(pyridin-3-ylsulfonyl)-1H-pyrrol-3-yl]-n-methylmethanamine fumarate (TAK-438) as a potassium-competitive acid blocker (P-CAB)[J]. Journal of Medicinal Chemistry, 2012, 55(9): 4446-4456. DOI:10.1021/jm300318t |
| [49] |
LIU K, WATANABE E, KOKUBO H. Exploring the stability of ligand binding modes to proteins by molecular dynamics simulations[J]. Journal of Computer-Aided Molecular Design, 2017, 31(2): 201-211. DOI:10.1007/s10822-016-0005-2 |
| [50] |
LIU K, KOKUBO H. Exploring the stability of ligand binding modes to proteins by molecular dynamics simulations:A cross-docking study[J]. Journal of Chemical Information and Modeling, 2017, 57(10): 2514-2522. DOI:10.1021/acs.jcim.7b00412 |
| [51] |
GUTERRES H, IM W. Improving protein-ligand docking results with high-throughput molecular dynamics simulations[J]. Journal of Chemical Information and Modeling, 2020, 60(4): 2189-2198. DOI:10.1021/acs.jcim.0c00057 |
| [52] |
LIU K, KOKUBO H. Prediction of ligand binding mode among multiple cross-docking poses by molecular dynamics simulations[J]. Journal of Computer-Aided Molecular Design, 2020, 34(11): 1195-1205. DOI:10.1007/s10822-020-00340-y |
| [53] |
ZHANG L, ZHOU R. Structural basis of the potential binding mechanism of remdesivir to SARS-CoV-2 RNA-dependent RNA polymerase[J]. The Journal of Physical Chemistry B, 2020, 124(32): 6955-6962. DOI:10.1021/acs.jpcb.0c04198 |
| [54] |
LEE T S, CERUTTI D S, MERMELSTEIN D, et al. GPU-accelerated molecular dynamics and free energy methods in amber18:Performance enhancements and new features[J]. Journal of Chemical Information and Modeling, 2018, 58(10): 2043-2050. DOI:10.1021/acs.jcim.8b00462 |
| [55] |
LEE T S, HU Y, SHERBORNE B, et al. Toward fast and accurate binding affinity prediction with pmemdGTI:An efficient implementation of GPU-accelerated thermodynamic integration[J]. Journal of Chemical Theory and Computation, 2017, 13(7): 3077-3084. DOI:10.1021/acs.jctc.7b00102 |
| [56] |
ROOS K, WU C, DAMM W, et al. OPLS3e:Extending force field coverage for drug-like small molecules[J]. Journal of Chemical Theory and Computation, 2019, 15(3): 1863-1874. DOI:10.1021/acs.jctc.8b01026 |
| [57] |
TIAN C, KASAVAJHALA K, BELFON K A A, et al. ff19SB:Amino-acid-specific protein backbone parameters trained against quantum mechanics energy surfaces in solution[J]. Journal of Chemical Theory and Computation, 2020, 16(1): 528-552. DOI:10.1021/acs.jctc.9b00591 |
| [58] |
LOEFFLER H H, MICHEL J, WOODS C. FESetup:Automating setup for alchemical free energy simulations[J]. Journal of Chemical Information and Modeling, 2015, 55(12): 2485-2490. DOI:10.1021/acs.jcim.5b00368 |
| [59] |
KLIMOVICH P V, SHIRTS M R, MOBLEY D L. Guidelines for the analysis of free energy calculations[J]. Journal of Computer-Aided Molecular Design, 2015, 29(5): 397-411. DOI:10.1007/s10822-015-9840-9 |
| [60] |
SHIRTS M R, CHODERA J D. Statistically optimal a-nalysis of samples from multiple equilibrium states[J]. The Journal of Chemical Physics, 2008, 129(12): 124105. DOI:10.1063/1.2978177 |