近几十年来,稀土(R)-过渡(T)金属间化合物因其丰富的物理特性如磁有序、自旋/价态涨落、超导电性、重费米子行为以及特殊的磁功能特性[1-2]等受到广泛关注。这些非常规的物理性质主要来源于稀土4f电子与过渡族d电子之间的复杂相互作用。其中,RAgSb2(R=La-Sm, Gd-Er)合金因其层状晶体结构表现出的丰富物理性质而引发研究者的极大兴趣。Sologub等[3]最早对RAgSb2的结构和磁性进行了系统的实验研究,发现这些材料具有ZrCuSi2型结构,YAgSb2和LaAgSb2表现为顺磁,CeAgSb2为非共线反铁磁,其他表现为弱反铁磁,并确定了这些合金的磁有序温度。随后陆续有学者开展了关于该体系的磁性、磁各向异性、输运[4]、角分辨光电子能谱[5]、中子衍射[6]以及热电性能[7]等相关研究,纠正了该体系的磁有序温度,并将CeAgSb2归为铁磁材料。正是由于该体系晶格中具有Sb-RSb-Ag-RSb-Sb的层状结构,使其表现出丰富的物理性质。Shi等[5]采用角分辨光电子能谱(Angle-Resolved Photoemission Spectroscopy, ARPES)结合第一性原理计算研究LaAgSb2整个布里渊区的电子结构,在费米能级附近观察到一个狄拉克锥状结构,该结构由两个线性能带的交叉,以及从锥体中出现的费米表面凹穴的嵌套部分组成,其ARPES结果显示了狄拉克锥与电荷密度波的有序关系,为这种材料中的奇异行为提供一致的解释。而CeAgSb2则被认为存在铁磁量子临界点[8],是一种典型的Kondo化合物。
RAgSb2合金是一个引人注目的体系,关于该合金的实验和理论研究从未间断。然而对于该体系的力学性能和热力学性能的研究还未见报道。因此,本研究采用基于密度泛函理论的第一性原理计算方法,对RAgSb2合金的结构、力学性能、声子以及热力学性质进行研究。
1 计算方法采用基于密度泛函理论的第一性原理计算方法,运用Materials Studio软件包中的CASTEP[9]模块,计算RAgSb2合金的结构稳定性、力学性能和热力学性质。将实验的晶格参数作为初始的参数,在Materials Studio的Visualizer模块中构建结构模型。然后对结构进行几何优化,使得几何结构稳定化以及能量最小化。结构优化采用Brodyden-Fletcher-Goldfarb-Shanno (BFGS)[10]最小化方法进行。几何优化的收敛标准:自洽迭代的能量为1.0×10-6 eV/atom,最大距离的收敛值为1.0×10-4 Å,原子间相互作用力的收敛标准为0.01 eV/Å,最大应力为0.02 GPa。晶体结构优化分别在局域密度近似泛函(LDA)和广义梯度近似泛函(GGA)下进行;电子和离子之间的相互作用势用超软赝势来模拟。经过收敛性测试后,计算的截断能为420 eV,第一布里渊区的k点用Monkhorst-Pack[11]方法确定,具体是6×6×3。R、Ag和Sb的最外层电子组态分别是4f1-145d0-16s2,4d105s1和5s25p3。
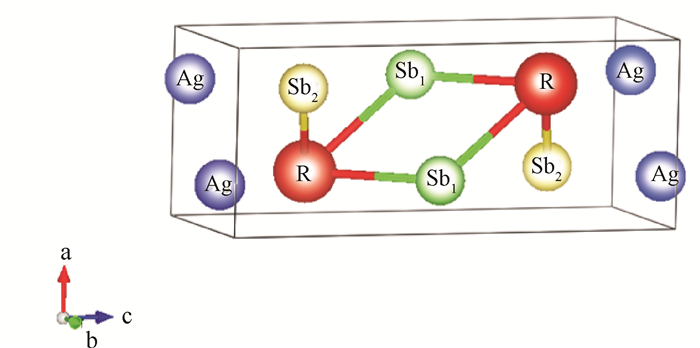
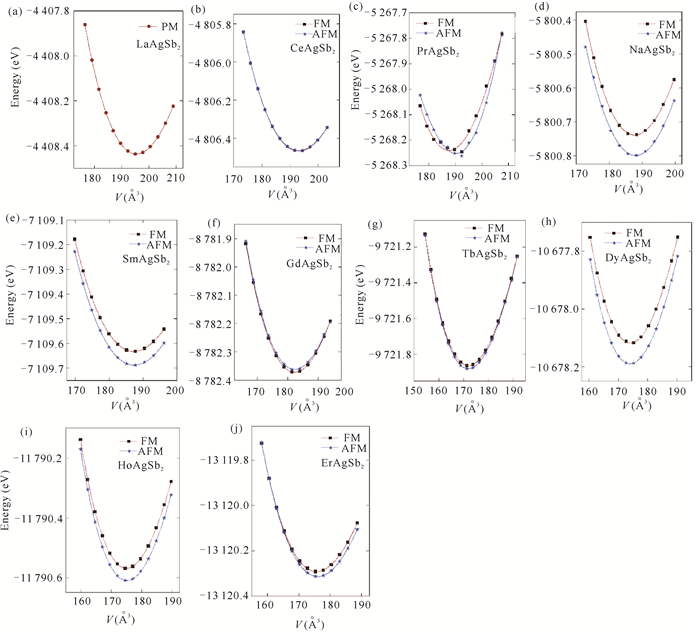
2 结果与分析 2.1 结构优化RAgSb2金属间化合物属于四方ZrCuSi2型晶体结构,空间群为P4/nmm (No.129),原子占位为Ag 2a (0.75, 0.25, 0)、Sb1 2c (0.25, 0.25, z1)、Sb2 2b (0.75, 0.25, 0.5)和R 2c (0.25, 0.25, z2),其晶体结构如图 1所示。图 2为这些合金能量随体积变化的Birch-Murnagha (B-M)方程拟合曲线。由于合金中含有磁性元素,因此除了LaAgSb2合金外,其他合金分别在铁磁和反铁磁条件下进行B-M方程拟合。由2图可得,RAgSb2(R=Pr-Sm, Tb-Er)合金在反铁磁态的能量最低,表明这些合金的磁基态为反铁磁,这一结果与之前文献的报道一致[4, 6]。CeAgSb2合金的铁磁和反铁磁的曲线几乎重合,而实验证明其本质上属于铁磁态[8]。计算结果表明GdAgSb2在铁磁态具有更低的能量,而实验观察到其属于反铁磁,具体原因有待进一步深入研究。表 1列出了这些合金的晶格常数。从表 1可以看出,随着稀土原子序数的增加,晶胞参数逐渐减小,呈现典型的镧系收缩效应,且理论计算的结果与实验结果符合,这表明我们的计算是可靠的。
|
| 图 1 RAgSb2合金的晶体结构 Fig. 1 Crystal structure of RAgSb2 alloys |
|
| 图 2 REAgSb2在铁磁和反铁磁态下总能随体积变化的拟合曲线 Fig. 2 Fitting curves of total energy versus volume for REAgSb2 under the ferromagnetic (FM) and antiferromagnetic (AFM) states |
| Compounds | Method | a (Å) | c (Å) | c/a | V (Å3) |
| LaAgSb2 | Experiment[6] | 4.389 80 | 10.842 0 | 2.469 8 | 208.929 |
| LDA | 4.341 01 | 10.456 8 | 2.408 8 | 197.052 | |
| GGA | 4.442 39 | 10.875 3 | 2.448 1 | 214.622 | |
| CeAgSb2 | Experiment[8] | 4.364 10 | 10.668 5 | 2.444 6 | 203.186 |
| LDA | 4.312 86 | 10.156 7 | 2.354 9 | 188.922 | |
| GGA | 4.415 48 | 11.346 5 | 2.569 7 | 221.217 | |
| PrAgSb2 | Experiment[8] | 4.347 90 | 10.668 5 | 2.453 7 | 201.680 |
| LDA | 4.299 03 | 10.453 2 | 2.431 5 | 193.192 | |
| GGA | 4.338 70 | 11.003 4 | 2.536 1 | 207.131 | |
| NdAgSb2 | Experiment[8] | 4.333 90 | 10.631 0 | 2.452 9 | 199.679 |
| LDA | 4.323 52 | 10.513 6 | 2.431 7 | 196.529 | |
| GGA | 4.491 78 | 11.008 1 | 2.450 7 | 222.100 | |
| SmAgSb2 | Experiment[8] | 4.312 60 | 10.548 0 | 2.445 8 | 196.177 |
| LDA | 4.359 26 | 10.028 0 | 2.300 4 | 190.564 | |
| GGA | 4.509 72 | 10.417 1 | 2.309 9 | 211.858 | |
| GdAgSb2 | Experiment[8] | 4.295 00 | 10.511 4 | 2.447 3 | 193.904 |
| LDA | 4.265 99 | 10.005 2 | 2.345 3 | 182.081 | |
| GGA | 4.342 78 | 10.542 1 | 2.427 5 | 198.821 | |
| TbAgSb2 | Experiment[8] | 4.277 40 | 10.477 0 | 2.449 3 | 191.689 |
| LDA | 4.169 05 | 10.082 1 | 2.418 3 | 175.237 | |
| GGA | 4.338 24 | 9.6978 9 | 2.235 4 | 182.517 | |
| DyAgSb2 | Experiment[8] | 4.265 60 | 10.454 5 | 2.450 8 | 190.223 |
| LDA | 4.190 53 | 9.8138 8 | 2.341 9 | 172.337 | |
| GGA | 4.304 92 | 10.364 8 | 2.407 6 | 192.084 | |
| HoAgSb2 | Experiment[8] | 4.267 00 | 10.420 2 | 2.442 0 | 189.724 |
| LDA | 4.177 68 | 10.206 7 | 2.443 1 | 178.138 | |
| GGA | 4.307 50 | 10.382 6 | 2.410 3 | 192.645 | |
| ErAgSb2 | Experiment[8] | 4.252 80 | 10.428 8 | 2.452 2 | 188.618 |
| LDA | 4.190 82 | 9.9292 9 | 2.369 3 | 174.388 | |
| GGA | 4.320 91 | 10.397 6 | 2.406 3 | 194.126 | |
| 注:a, c, V分别表示这些沿着x, z方向的长度和晶体体积 Note:a, c and V represent the length along the x, z direction and crystal volume, respectively | |||||
结合能可表征晶体的稳定性,可表述为将自由原子结合为晶体所释放的能量。RAgSb2合金的结合能用如下公式计算:
| $ {E_{coh}} = \frac{{{E_{tot}} - {N_{Ag}}E_{atom}^{Ag} - {N_{RE}}E_{atom}^R - {N_{Sb}}E_{atom}^{Sb}}}{{{N_{Ag}} + {N_R} + {N_{Sb}}}}, $ | (1) |
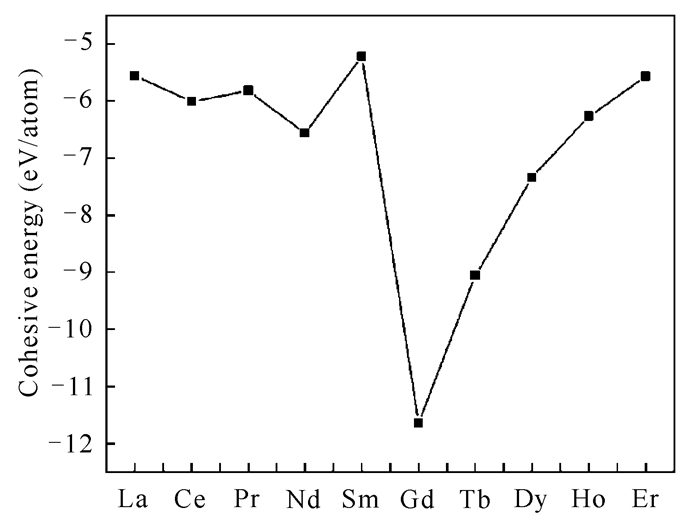
式中,Etot是总能,EatomAg、EatomR、EatomSb分别是孤立态的Ag、R和Sb原子的能量,NR、NAg和NSb分别是原子在单胞中的原子个数,计算结果如表 2所示。从表 2可以得出这些合金的结合能均为负值,表明这些合金具有稳定的结构。图 3为不同稀土元素结合能的变化情况,其中GdAgSb2的结合能绝对值最大,表明这个合金的结构最稳定;重稀土的结合能绝对值逐渐减小,即这些合金的结构稳定性逐渐减弱,这可能是由于镧系收缩,稀土原子与其他原子键合作用减弱。
|
| 图 3 RAgSb2合金的结合能 Fig. 3 Cohesive energy of RAgSb2 alloys |
| Compounds | Ecoh(eV/atom) |
| LaAgSb2 | -5.56 |
| CeAgSb2 | -6.01 |
| PrAgSb2 | -5.82 |
| NdAgSb2 | -6.57 |
| SmAgSb2 | -5.22 |
| GdAgSb2 | -11.64 |
| TbAgSb2 | -9.06 |
| DyAgSb2 | -7.34 |
| HoAgSb2 | -6.27 |
| ErAgSb2 | -5.57 |
2.2 机械性能
弹性常数Cij是表征力学性能的重要参数,既可用于估算材料的力学性质,也可用来表征固体抵抗外力变形的能力[12]。本研究根据胡克定律计算RAgSb2合金的弹性常数。晶体只有满足相应晶系的稳定性判据才能稳定存在。对于四方结构,有6个独立弹性常数,分别是C11、C12、C13、C33、C44和C66,这些弹性常数需要满足Born-Huang条件:
| $ {{C_{11}} - {C_{12}} > 0,} $ | (2) |
| $ {{C_{11}} + {C_{33}} - 2{C_{13}} > 0,} $ | (3) |
| $ {2({C_{11}} + {C_{12}}) + {C_{33}} + 4{C_{13}} > 0}。$ | (4) |
表 3列出了RAgSb2合金的弹性常数值和柯西压力值。计算发现,这一系列合金的弹性常数均满足上述条件,表明这些合金具有稳定的机械性能。C11、C22、C33分别表示抵抗a轴、b轴和c轴方向形变的能力,对于四方结构的晶体,C11=C22[13]。从表 3可以明显看出,除了ErAgSb2合金外,其余合金的C11值均大于C33,说明这些合金在沿着a轴或者b轴方向抵抗形变的能力比c轴方向强,且抵抗变形的能力具有先减小后增大再减小的变化趋势;而ErAgSb2合金则刚好相反。此外,C11和C33的值均大于其他的弹性常数值,这表明这些合金具有弹性各向异性。C44和C66分别表示(100)面和沿着 < 110>方向的剪切阻力。从图 4中可以看出,这些合金在(100)面上抵抗剪切阻力的能力相差不大,而在 < 110>方向抵抗力的能力强弱不一样,这可能与该方向成键能力有关。通过弹性常数可计算柯西压力值,用来描述化合物的成键特征。对于四方结构,柯西压力可用C13-C44来计算[14]。当柯西压力为正时,晶体以金属键合,表现为韧性,当其为负时晶体以定向的共价键相连,表现为脆性。从表 3中可以看出,除了GdAgSb2和TbAgSb2的柯西压力值为正,其余合金的值均为负,表明GdAgSb2和TbAgSb2合金的成键方式为金属键,具有韧性;而其余的合金以共价键方式成键,表现为脆性。
| Compounds | C11(GPa) | C33(GPa) | C44(GPa) | C66(GPa) | C12(GPa) | C13(GPa) | C13-C44(GPa) |
| LaAgSb2 | 148.08 | 98.00 | 56.43 | 45.39 | 47.32 | 44.31 | -12.12 |
| CeAgSb2 | 153.89 | 96.47 | 52.55 | 25.16 | 46.89 | 43.15 | -9.4 |
| PrAgSb2 | 138.04 | 80.95 | 46.69 | 37.62 | 44.07 | 35.34 | -11.35 |
| NdAgSb2 | 105.91 | 48.06 | 29.75 | 31.63 | 21.87 | 10.78 | -18.97 |
| SmAgSb2 | 114.08 | 61.33 | 42.44 | 38.39 | 20.72 | 28.39 | -14.05 |
| GdAgSb2 | 133.25 | 90.91 | 51.82 | 51.08 | 68.89 | 66.72 | 14.9 |
| TbAgSb2 | 167.46 | 100.88 | 42.26 | 22.89 | 73.54 | 56.41 | 14.15 |
| DyAgSb2 | 156.74 | 127.40 | 50.92 | 67.09 | 55.81 | 38.05 | -12.87 |
| HoAgSb2 | 146.47 | 69.68 | 42.85 | 73.82 | 65.62 | 42.53 | -0.42 |
| ErAgSb2 | 166.20 | 252.22 | 51.39 | 71.49 | 61.15 | 48.21 | -3.18 |
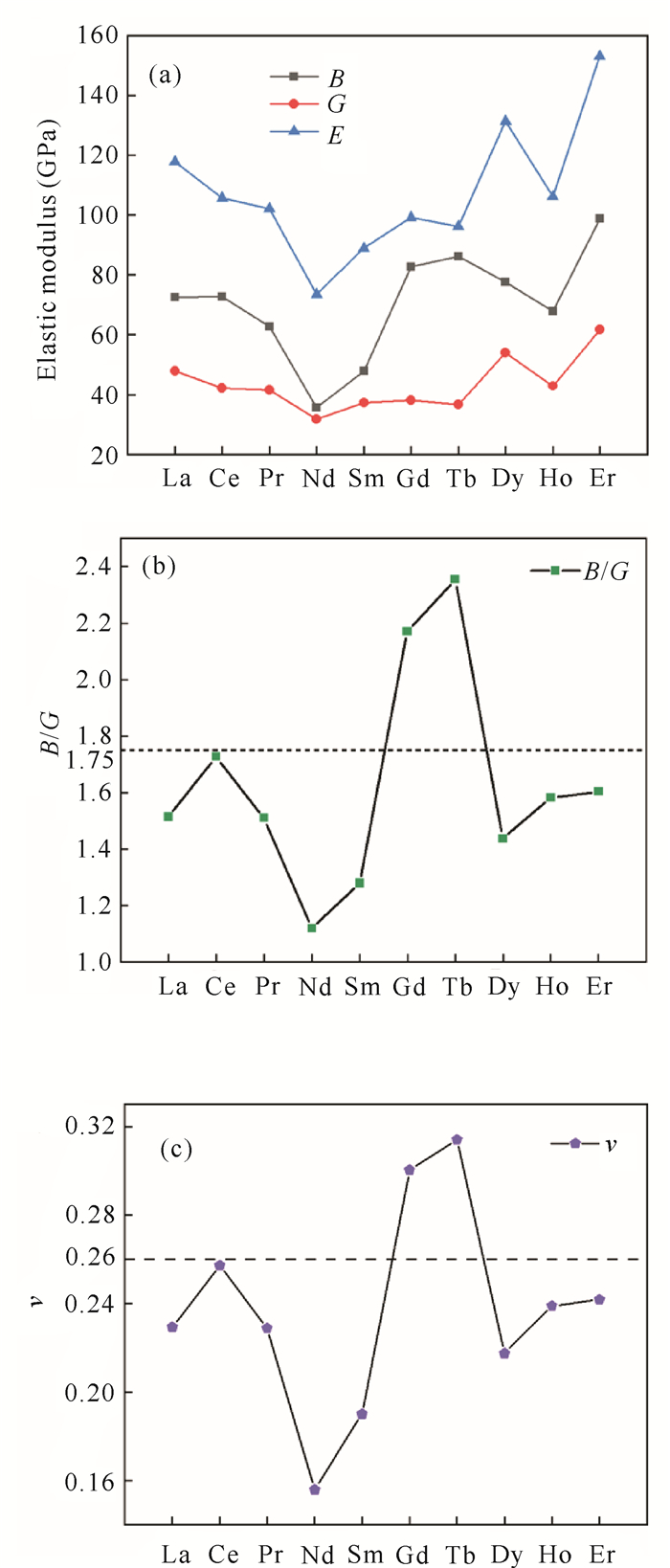
|
| 图 4 RAgSb2合金的弹性模量,B/G和泊松比v Fig. 4 Elastic modulus, B/G and Possion ratio v of RAgSb2 alloys |
利用弹性常数可以计算多晶样品的体积模量B和剪切模量G, 其中Voigt提出的计算这些模量的方法分别用BV和GV表示;Ruess得到的弹性模量的方法分别用BR和GR表示;Hill总结前两种方法,提出了Voigt-Ruess-Hill (VRH)近似[15],相应的计算公式如下:
| $ {{B_V} = (1/9)[2({C_{11}} + {C_{12}}) + {C_{33}} + 4{C_{13}}],} $ | (5) |
| $ {{G_V} = (1/30)(M + 3{C_{11}} - 3{C_{12}} + 12{C_{44}} + 6{C_{66}}),} $ | (6) |
| $ {{B_R} = {C^2}/M,} $ | (7) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_R} = 15\{ (18{B_V}/{C^2}) + [6/({C_{11}} - {C_{12}})] + \\ {C_{44}}) + (3/{C_{66}}){\} ^{ - 1}}, \end{array} $ | (8) |
| $ {M = {C_{11}} + {C_{12}} + 2{C_{33}} - 4{C_{13}},} $ | (9) |
| $ {{C^2} = ({C_{11}} + {C_{12}}){C_{33}} - 2C_{13}^2,} $ | (10) |
| $ {B = \frac{{{B_V} + {B_R}}}{2},} $ | (11) |
| $ {G = \frac{{{G_V} + {G_R}}}{2}}。$ | (12) |
杨氏模量E和泊松比v可通过体积模量与剪切模量得到,具体计算公式如下:
| $ {E = \frac{{9BG}}{{3B + G}},} $ | (13) |
| $ {v = \frac{{3B - 2G}}{{2(3B + G)}}}。$ | (14) |
体积模量常用来表征材料在静水压力作用下的抗变形能力,而剪切模量则用来描述材料在剪切应力作用下的抗变形能力[16]。杨氏模量可用来表征材料的刚度,杨氏模量越大,材料抵抗弹性变形的能力越强。从图 4可以得出,ErAgSb2的体积模量、剪切模量和杨氏模量均是最大,而NdAgSb2相应的模量最小,表明该化合物的强度最大,当受到一定的应力时,不易产生弹性变形。体积模量值均大于剪切模量,表明这一系列合金物具有较强的抵抗体积变化的特性。
B/G常用来预测材料的塑性和脆性。根据Pugh标准[17],当B/G>1.75时,材料具有良好的延展性,而当B/G小于1.75时,材料具有脆性。图 4b中虚线值为1.75,可以看出GdAgSb2和TbAgSb2的B/G值大于1.75,即这两个合金具有好的延展性,而其余合金的值均小于1.75,表现出脆性。泊松比可以用来表征材料的脆性和韧性[18]。通常,当泊松比v>0.26时,材料具有韧性;反之,当v < 0.26时,材料具有塑性行为。由图 4c可得,GdAgSb2和TbAgSb2的值大于0.26,即这两个合金表现为韧性,其余的合金为脆性,这与柯西压力的计算结果一致。
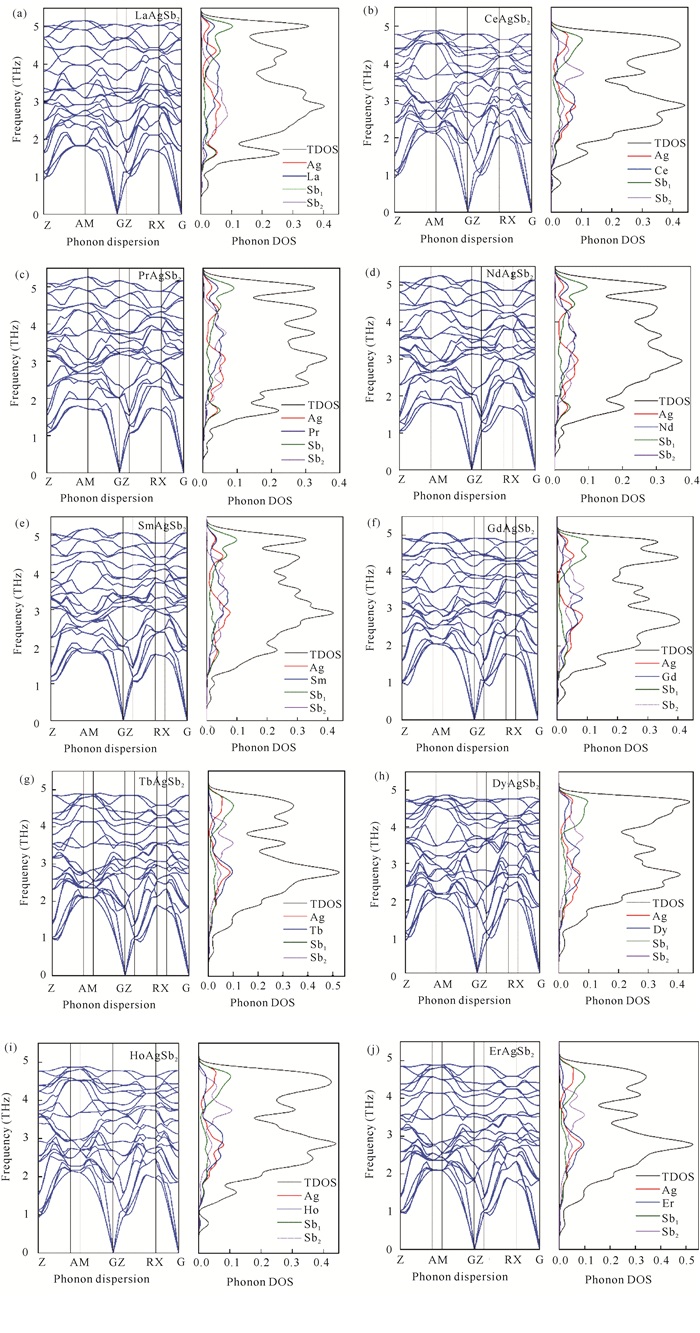
2.3 声子与热力学性质声子可以用来判断固体在晶格振动学上的稳定性。如图 5所示,RAgSb2合金的声子谱在布里渊区中均未出现虚频,且声子态密度也未出现负值,说明这一系列合金具有热力学稳定性。这些合金的原胞中包含8个原子,理论上的色散关系有24种,即有24条声子谱线,包括3条声学波,21条光学波。声学波表示原胞质心的振动,光学波表示晶格中粒子的相对振动[19]。从图 5中可以明显看出,计算的声子谱线为24条,与理论值一致。这一系列合金具有相同的晶体结构和类似的原子占位,因此它们的声子谱类似。在A-M和R-X区间的色散关系是双重简并的,而在其他区域是非简并分布。由于库仑相互作用的影响,纵向的光学(LO)模式的频率高于横向光学(TO)模式的频率。值得注意的是,在G点有(3—4)×1012 Hz的LO/TO分离,而在其他范围内是简并的。因此在本研究中没有考虑LO/TO分离对热力学性质的影响。从声子态密度可以发现,当频率为(4—5)×1012 Hz时,总的声子态密度主要由2b (0.75, 0.25, 0.5)位置的Sb贡献,R和Ag也有部分贡献;在(3—4)×1012 Hz的总态密度是由稀土贡献;在(0—3)×1012 Hz主要由Ag、Sb1和Sb2贡献。
|
| 图 5 RAgSb2合金的声子谱和声子态密度 Fig. 5 Phonon dispersion and DOS of RAgSb2 alloys |
图 6为RAgSb2合金的形成焓H、自由能G、熵S以及热容CV随温度变化的关系。由图 6可知,这些合金的热力学性质差异很小,这与它们具有类似的声子色散关系的事实吻合,形成焓H和熵S均随温度的升高而增加。由G=H-TS公式可得,自由能G降低,是由于S增加的速度比H增加的速度快导致的。对于热容CV,随着温度的升高,在低温下急剧增加并与T3成正比,在较高温度下缓慢增加并最终趋向于Dulong-Petit极限,这些合金在高温下的热容接近47.5 cal·cell-1·K-1 (缺乏可用于比较的实验数据)。

|
| 图 6 RAgSb2合金的热力学性质:形成焓H、自由能G、熵S以及热容CV Fig. 6 Themodynamic properties:Enthalpy H, Gibbs energy G, entropy S and heat capacity CV of RAgSb2 alloys |
3 结论
由B-M方程拟合可得到,RAgSb2合金中除了CeAgSb2和GdAgSb2,其余合金的基态性质均为反铁磁。负的结合能数值证实了该系列合金具有热力学稳定性。RAgSb2合金的弹性常数满足相应的Born-Huang条件,表明这些合金具有稳定的机械性能。RAgSb2合金的体积模量(B)值均大于剪切模量(G),说明它们抵抗形变的能力较弱,抵抗体积变形的能力较强。泊松比、B/G和柯西压力的计算结果表明,GdAgSb2和TbAgSb2合金的成键方式为金属键,具有韧性;而其余的合金以共价键方式成键,表现为脆性。RAgSb2合金的声子谱中未见虚频,进一步证实了这些合金具有稳定的热力学性质。同时,类似的声子色散关系使得这些合金的热力学性质差别很小。热容CV在低温下随着温度的升高急剧增加并与T3成正比,而在较高温度下缓慢增加并趋向于Dulong-Petit极限,且高温下的热容近似为47.5 cal·cell-1·K-1。
| [1] |
SINGH N K, SURESH K G, NIGAM A K, et al. Correlation between magnetism and magnetocaloric effect in RCo2-based Laves phase compounds[J]. Physics, 2006, 317(1/2): 68-79. |
| [2] |
BAZINE W, TAHIRI N, EL BOUNAGUO O, et al. Structural, electronic, magnetic, and magnetocaloric properties in intermetallic compound TbCu2Si2[J]. Journal of Magnetism and Magnetic Materials, 2019, 481: 72-76. DOI:10.1016/j.jmmm.2019.02.095 |
| [3] |
SOLOGUB O, HIEBL K, ROGL P, et al. On the crystal structure and magnetic properties of the ternary rare earth compounds RETSb2 with RE=rare earth and T=Ni, Pd, Cu and Au[J]. Journal of Alloys and Compounds, 1994, 210(1): 153-157. |
| [4] |
MYERS K D, BUD″KO S L, FISHER I R, et al. Syste-matic study of anisotropic transport and magnetic properties of RAgSb2 (R=Y, La-Nd, Sm, Gd-Tm)[J]. Journal of Magnetism and Magnetic Materials, 1999, 205(1): 27-52. DOI:10.1016/S0304-8853(99)00472-2 |
| [5] |
SHI X, RICHARD P, WANG K, et al. Observation of Dirac-like band dispersion in LaAgSb2[J]. Physical Review B, 2015, 93: 081105. |
| [6] |
ANDRE' G, BOURE'E F, KOLENDA M, et al. Magnetic structures of RAgSb2 compounds[J]. Physica B:Condensed Matter, 2000, 292(1/2): 176-189. |
| [7] |
MUN E D, BUD'KO S L, CANFIELD P C. Thermoelectric power of RAgSb2 (R=Y, La, Ce, and Dy) in zero and applied magnetic fields[J]. Journal of Physics Condensed Matter, 2011, 23(47): 476001. DOI:10.1088/0953-8984/23/47/476001 |
| [8] |
KAWASAKI I, OGATA S, KAWAI S, et al. Magnetic properties of 4f localized ferromagnet CeAgSb2 under transverse magnetic fields[J]. Journal of the Physical Society of Japan, 2018, 87(1): 014703. DOI:10.7566/JPSJ.87.014703 |
| [9] |
CLARK S J, SEGALLⅡ M D, PICKARDⅡ C J, et al. First principles methods using CASTEP[J]. Zeitschrift für Kristallographie, 2005, 220(5/6): 567-570. |
| [10] |
FISCHER T H, ALMLOF J. General methods for geometry and wave function optimization[J]. Journal of Physical Chemistry, 1992, 96(24): 9768-9774. DOI:10.1021/j100203a036 |
| [11] |
MONKHORST H J, PACK J D. Special points for Brillouin-zone intergrations[J]. Physical Review B, 1976, 13(12): 5188-5192. DOI:10.1103/PhysRevB.13.5188 |
| [12] |
RAVINDRAN P, FAST L, KORZHAVYI P A, et al. Density functional theory for calculation of elastic properties of orthorhombic crystals:Application to TiSi2[J]. Journal of Applied Physics, 1998, 84(9): 4891-4904. DOI:10.1063/1.368733 |
| [13] |
GAO X P, JIANG Y H, ZHOU R, et al. Stability and elastic properties of Y-C binary compounds investigated by first principles calculations[J]. Journal of Alloys and Compounds, 2014, 587: 819-826. DOI:10.1016/j.jallcom.2013.11.005 |
| [14] |
PAPADIMITRIOU I, UTTON C, SCOTT A, et al. Ab initio study of the intermetallics in Nb-Si binary system[J]. Intermetallics, 2014, 54: 125-132. DOI:10.1016/j.intermet.2014.05.020 |
| [15] |
HILL R W. The elastic behavior of a crystalline aggregate[J]. Proceedings of the Physical Society Section A, 2002, 65(5): 349. |
| [16] |
LI R Y, DUAN Y H. Anisotropic elastic properties of MB (M=Cr, Mo, W) monoborides:A first-principles investigation[J]. Philosophical Magazine, 2016, 96(10): 972-990. DOI:10.1080/14786435.2016.1149247 |
| [17] |
PUGH S F. XCⅡ.Relations between the elastic moduli and the plastic properties of polycrystalline pure metals[J]. The London Edinburgh and Dublin Philosophical Magazine and Journal of Science, 1954, 45(367): 823-843. DOI:10.1080/14786440808520496 |
| [18] |
XING D, ZHANG T, LI W, et al. Characterization of plastic flow in two Zr-based bulk metallic glasses[J]. Science in China, 2006, 49(4): 414-424. DOI:10.1007/s11431-006-0414-x |
| [19] |
张智勇.AlN晶体声子谱及其热学性能的第一性原理计算[D].沈阳: 沈阳工业大学, 2013.
|



