近年来,针对具有A5B3型化合物的研究越来越多,这是因为该类化合物具有独特的物理化学性能[1-5],研究表明超过40个金属间化合物具有A5B3型结构。常见的结构类型有Cr5B3型、W5Si3型和Mn5Si3型这3类,Tao等[5-8]利用基于密度泛函的第一性原理方法对Ta5Si3、W5Si3、V5Si3以及Tl5Te3等化合物的物理化学性能进行模拟计算研究,获得了这些化合物的结构稳定性、力学性能、电子结构特性以及热物理性能和热电性能等。含碱土金属Ca的化合物中,Ca5Si3因其有潜在的储氢性能[3]和热电性能[9]备受关注。然而在含Ca的化合物中,Ca5Zn3也具有Cr5B3型结构[1]。2012年,Yang等[10]利用基于密度泛函的第一性原理的方法对Ca-Zn体系的7个化合物进行了计算研究,计算获得了形成焓、弹性常数和电子态密度等信息。然而,至今还没有针对Ca5Zn3的更加系统研究的报道。为了能够获得更加系统的物理性能,本文将利用基于密度泛函的第一性原理方法对Ca5Zn3化合物进行系统计算研究,获得该化合物的热力学稳定性、力学性能、电子结构特性,并结合德拜模型对其热物理性能进行研究和预测。
1 材料与方法 1.1 Ca5Zn3的晶体结构采用Cr5B3型、W5Si3型和Mn5Si3型等3种结构来讨论Ca5Zn3结构稳定性。其中Cr5B3型结构是一个四方晶系的结构,Pearson符号为tI32,共有4种不同占位,Cr占据16l和4c位,B占据4a和8h位。每个Cr5B3型结构单胞中含有10个Cr原子,6个B原子。其余两种结构的具体信息可参见文献[5]。3种晶体结构如图 1所示。

|
| (a) Cr5B3型,(b) W5Si3型,(c) Mn5Si3型; 蓝色为Ca原子,灰色为Zn原子 (a) Cr5B3 prototype, (b) W5Si3 prototype, (c) Mn5Si3 prototype; the blue atom is Ca, the grey atom is Zn 图 1 Ca5Zn3化合物的3种晶体结构 Fig. 1 Tree crystal structures of Ca5Zn3 compounds |
1.2 计算方法
本文采用基于密度泛函理论(Density Functional Theory,DFT)的第一性原理计算软件包Vienna Ab initio Simulation Package (VASP)[11]进行计算。第一性原理计算方法是投影缀加波方法[12-13],交换关联势采用广义梯度近似的Perdew-Burke-Ernzerhof (PBE)方案[14]。布里渊区积分采用Monkhorst Pack布点方法[15],对于Cr5B3和W5Si3结构,K点取11×11×11,而对Mn5Si3结构,K点为9×9×11。在本文计算中, 波函数的截断能设置为500 eV,能量收敛精度为10-6 eV。在进行性能计算前,所有结构都进行全优化,直到原子间的力小于0.01 eV/Å为止,以保证计算的准确性。有关形成焓、弹性常数以及热物理性质的计算方法参见文献[5]。
Ca5Zn3化合物形成焓可以用以下的公式进行计算:
| $ \begin{array}{c} \mathit{\Delta} H\left(\mathrm{Ca}_{5} \mathrm{Zn}_{3}\right)=E_{\text {total }}\left(\mathrm{Ca}_{5} \mathrm{Zn}_{3}\right)-5 E_{\text {total }}(\mathrm{Ca}) \\ 3 E_{\text {total }}(\mathrm{Zn}), \end{array} $ | (1) |
其中,Etotal(Ca5Zn3)、Etotal(Ca)和Etotal(Zn)分别是Ca5Zn3合金、Ca以及Zn元素的总能量。
晶体弹性常数是一种反映材料基本性质的常数,它描述了晶体对外加应变的响应刚度。当忽略温度对体系总能的影响时,在应变很小的情况下,体系的内能与应变的大小存在二次线性关系(胡克定律),弹性常数就是描述这种二次线性关系,即二次线性项的系数。为了计算弹性常数,我们通过设定一组形变量,求解固体在不同形变下所对应的总能量,利用弹性理论公式拟合这组能量就可以得到它们的弹性常数。通过定义一个应变张量ε,可使基矢
| $ {{\vec a}^\prime } = (\vec I + \varepsilon )\vec a, $ | (2) |
| $ \varepsilon = \left( {\begin{array}{*{20}{c}} {{\varepsilon _1}}&{{\varepsilon _6}/2}&{{\varepsilon _5}/2}\\ {{\varepsilon _6}/2}&{{\varepsilon _2}}&{{\varepsilon _4}/2}\\ {{\varepsilon _5}/2}&{{\varepsilon _4}/2}&{{\varepsilon _2}} \end{array}} \right), $ | (3) |
| $ \begin{array}{*{20}{c}} {E(V,\varepsilon ) = E\left( {{V_0},0} \right) + {V_0}\sum\limits_i {{\sigma _i}} {\varepsilon _i} + }\\ {\frac{{{V_0}}}{2}\sum\limits_{ij} {{C_{ij}}} {\varepsilon _i}{\varepsilon _j} + O\left( {\varepsilon _i^3} \right),} \end{array} $ | (4) |
其中,V0是晶格平衡时的体积。上式第二项是一个线性项,如果体积没有变化或者在平衡位置处,该项为零;O(εi3)是在展开的多项式中忽略εi的立方项或者更高次项。
Cr5B3结构类型的Ca5Zn3是四方晶系。四方晶系有6个独立弹性常数,分别为C11, C12, C13, C33, C44和C66。通过下面6个形变矩阵可以求得相应弹性常数(表 1)。
| 形变矩阵 Deformation matrix |
形变后能量表达式 Energy expression after deformation |
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
德拜温度作为一个基本的物理参数,与热容、弹性常数等有着密切联系。一般来说,德拜温度越高,化合物熔点越高,意味着原子间的相互作用越强。一般来说,德拜温度(Θ)可以从平均声速(um)进行估算:
| $ \mathit{\Theta}=\frac{h}{k_{B}}\left(\frac{3}{4 \pi V}\right)^{1 / 3} u_{m}, $ | (5) |
其中, h和kB分别是普朗克常数和玻尔兹曼常数,V是原子平均体积,在多晶体中的平均声速(um)可以用以下公式计算:
| $ u_{m}=\left[\frac{1}{3}\left(\frac{2}{u_{t}^{3}}+\frac{1}{u_{l}^{3}}\right)\right]^{-1 / 3},$ | (6) |
其中,ut和ul分别是横向声速和纵向声速,这两种声速可以通过以下公式获得:
| $ {{u_t} = {{\left( {\frac{G}{\rho }} \right)}^{1/2}},} $ | (7) |
| $ {{u_l} = {{\left( {\frac{{3B + 4G}}{{3\rho }}} \right)}^{1/2}},} $ | (8) |
其中, G为剪切模量,B为体积模量,ρ为质量密度。
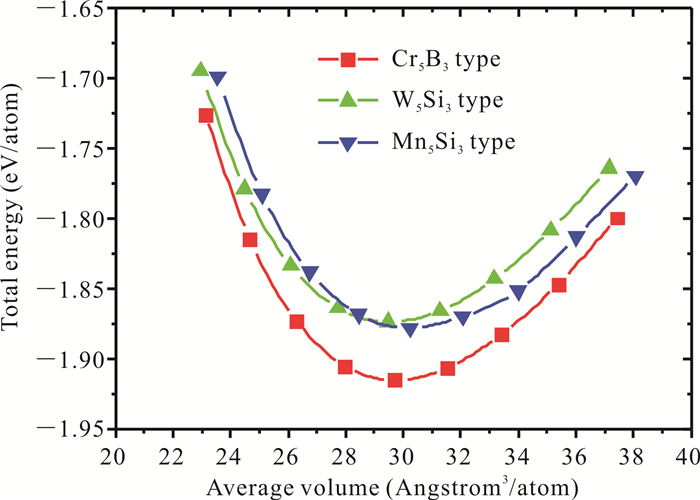
2 结果与分析 2.1 结构稳定性能为了获得Ca5Zn3的结构稳定性,考虑了Cr5B3型、W5Si3型和Mn5Si3型3种晶体结构,计算获得的晶格常数、形成焓(表 2),同时分析3种晶体结构的总能随体积变化的关系(图 2)。本文计算获得的Cr5B3型晶格常数为7.865 6 Å和15.366 3 Å,Bottcher等[1]的实验值为7.963 Å和15.407 Å,其他第一性原理计算值[10]为7.802 Å和15.620 Å。本文的晶格常数计算值与实验值之间的误差为1.22%和0.26%,比Yang等[10]计算值的误差(2.02%,1.38%)小,说明本文计算获得的晶格常数更为合理。W5Si3型和Mn5Si3型Ca5Zn3化合物的晶格常数也作为预测结果列于表 2。从表 2中给出的形成焓可以看出,Cr5B3型Ca5Zn3的形成焓最低为-0.201 eV/atom,其他两种晶体结构的形成焓分为-0.160 eV/atom和-0.164 eV/atom。从能量的角度,其他两种晶体结构的形成焓比Cr5B3型的形成焓高出0.04 eV/atom,因此,具有Cr5B3结构的Ca5Zn3是最稳定的化合物。从图 2中可以看出,具有Cr5B3型的Ca5Zn3具有最低的总能量,同样表明Cr5B3型Ca5Zn3是最稳定的化合物,这与Bottcher等[1]的实验结果是一致的。
|
| 图 2 具有3种不同晶体结构的Ca5Zn3化合物总能量与体积的关系 Fig. 2 Relationship of total energy and volume of Ca5Zn3 compounds with three different crystal structures |
2.2 力学性能
为了研究Ca5Zn3的力学性能,本文计算了稳定相的晶格常数,由上文可知Cr5B3型晶体结构属于四方晶系,其独立的弹性常数为6个,为此,本文利用应力应变的方法[16]对其弹性常数进行了计算(表 3)。根据四方晶系力学稳定性条件:C11>0, C33>0, C44>0, C66>0, (C11-C12)>0, (C11+C33-2C13)>0和(C11+C12)C33-2C132>0,本文计算获得的Ca5Zn3的弹性常数都满足力学稳定性条件,表明该化合物具有静力学稳定性。C11大于C33,由此可见在[100]和[010]方向上的键强度高于[001]方向上的键强度。多晶体的体积模量、剪切模量以及杨氏模量都可以从弹性常数给出[5]。本文计算得到的体积模量和Yang等[10]报道的计算值吻合,而剪切模量的计算值比Yang等[10]报道的计算值稍小,这是由于本文计算的C33比Yang等[10]报道的计算值稍小导致的。
| 数据来源 Data source |
C11 (GPa) |
C12 (GPa) |
C13 (GPa) |
C33 (GPa) |
C44 (GPa) |
C66 (GPa) |
BH (GPa) |
BV (GPa) |
BR (GPa) |
GH (GPa) |
GV (GPa) |
GR (GPa) |
E (GPa) |
v | B/G | A1 | A2 | ut (m/s) |
ul (m/s) |
um (m/s) |
Θ (K) |
|
| Present | 40.54 | 18.53 | 22.69 | 28.79 | 14.60 | 10.8 | 26.16 | 26.41 | 25.92 | 10.02 | 11.06 | 8.98 | 26.66 | 0.330 | 2.61 | 0.98 | 1.33 | 190 1 | 307 2 | 209 7 | 202 | |
| [10] | 42.8 | 19.3 | 20.8 | 34.3 | 13.9 | 19.1 | 26.7 | 26.9 | 26.6 | 12.8 | 13.3 | 12.2 | 33.1 | 0.294 | 2.04 | |||||||
| 注:C11、C12、C13、C33、C44、C66为弹性常数;BH、BV、BR为体积模量;GH、GV、GR为剪切模量;E为杨氏模量;v为泊松比;A1、A2为各向异性因子;ut、ul、um为声速,Θ为德拜温度 Note:Elastic constants (C11, C12, C13, C33, C44, C66), bulk modulus (BH, BV, BR), shear modulus (GH, GV, GR), Young's modulus (E), Poisson's ratio (v), elastic anisotropic parameters (A1, A2), sound velocities (ut, ul, um), Debye temperature (Θ) | ||||||||||||||||||||||
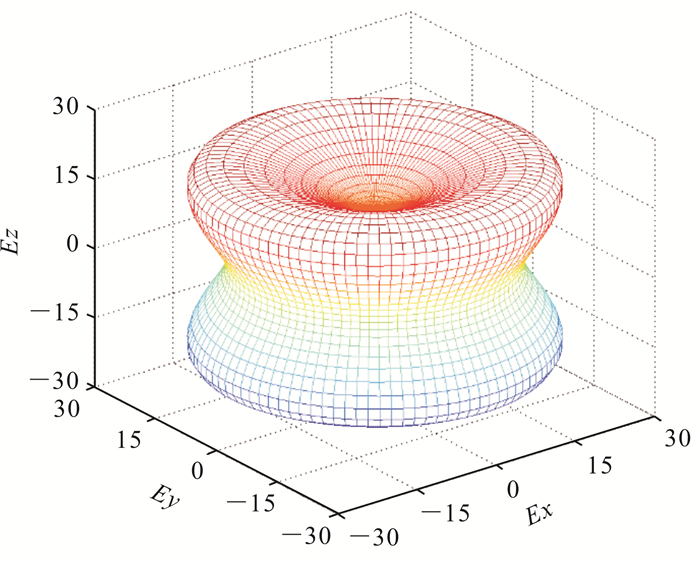
B/G值一般用来预测化合物的脆韧性[17],该比值大于1.75,化合物呈现韧性,比值越大韧性越大;反之,该比值小于1.75,则化合物呈现脆性,且比值越小脆性越大。Ca5Zn3的B/G值为2.61,说明该化合物呈现韧性。为了研究化合物的各向异性,对于四方晶系来说,一般用A1=2C66/(C11-C12)和A2=2C44/(C11-C12)进行说明。该数值为1时,则呈现各向同性,偏离1越远则各向异性越明显。为了更加明显地呈现该化合物的各向异性,图 3给出了杨氏模量的空间分布图,由此可以清晰地看出在不同的方向上,杨氏模量的数值存在明显的差异。
|
| 图 3 Ca5Zn3化合物杨氏模量的空间分布(GPa) Fig. 3 Spatial distribution of Young's modulus for Ca5Zn3 compounds (GPa) |
2.3 电子结构特性
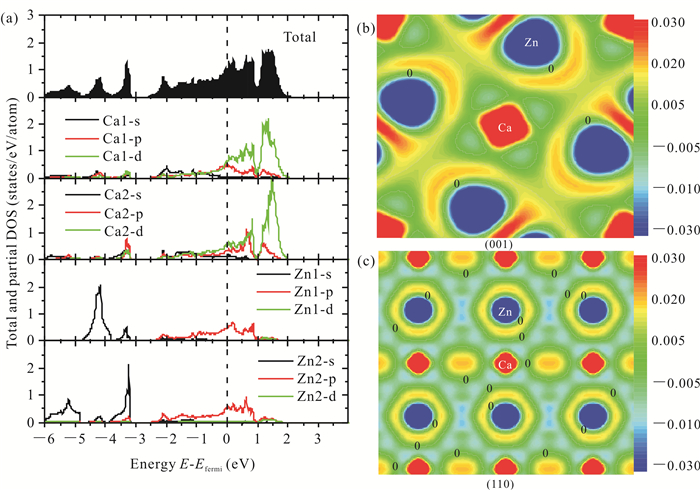
为了深入了解该化合物原子间的相互作用,本文计算了该化合物的电子态密度和电荷密度差(图 4)。由图 4a可以看出,在费米面以下的电子态密度,主要是Ca的s电子和p电子以及Zn的s电子和p电子的贡献,费米面以上的电子态密度主要是Ca的d电子和Zn的p电子的贡献。在费米面附近,Ca的p电子和d电子跟Zn的p电子发生杂化效应。在费米能外态密度不为零,说明该化合物呈现金属性。由图 4b和图 4c可知,Ca和Zn之间主要呈现离子键特性,Ca失去电子,而Zn则获得电子,这个和图 4a中的电子态密度在费米面附近发生杂化效应是一致的。由于Ca的电负性为1.0,Zn的电负性为1.6,电负性越大表明越容易获得电子,由此可见本文的计算结果是合理的。
|
| (a)电子态密度,(b) (001)面,和(c) (110)面 (a) electronic density of state, (b) (001) plane and (c) (110) plane 图 4 Ca5Zn3的电荷密度差 Fig. 4 Charge density difference of Ca5Zn3 |
2.4 热物理性能
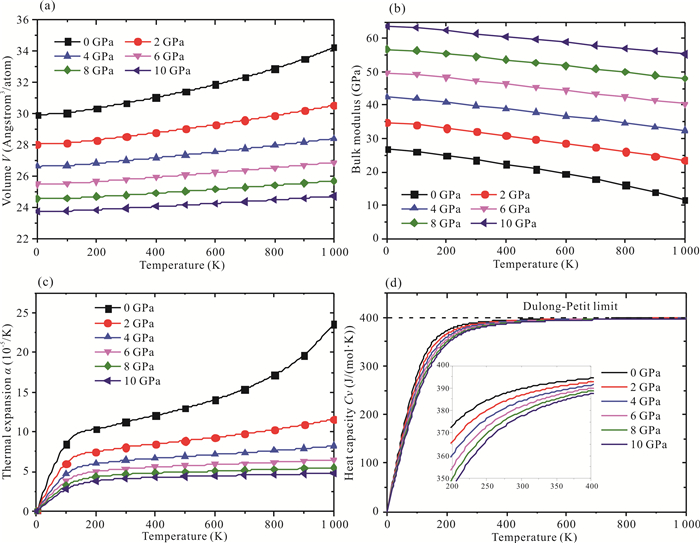
Ca5Zn3化合物的德拜温度为202 K。平均声速为2 097 m/s,纵向声速为3 072 m/s,横向声速为1 901 m/s (表 3)。利用德拜模型[18-21],结合第一性原理总能量的计算结果,计算了Ca5Zn3化合物在0—1 000 K温度范围、0—10 GPa压强范围内的热物理性质(图 5)。由图 5a可知,化合物的体积随着温度的升高而增加,但是随着压强的增加则降低。并且随着压强的越来越大,体积减小的幅度越来越小,说明原子间的作用力也越来越大。图 5b给出了体积模量随温度和压强的变化关系,随着温度的升高,体积模量有所下降,但是随着压强的增加,体积模量也在增加。图 5c表示热膨胀系数随着温度的升高而增加,随着压强的增大而热膨胀系数增加的幅度降低。在6 GPa以上时,随着温度的上升,热膨胀系数增加的幅度极小。表明在高压下,热膨胀系数变化小,体积膨胀不明显。图 5d展示的是定容热容随温度和压强的变化关系,在0—300 K区间,定容热容急速增加,在300—400 K区间,等容热容的上升趋势变缓,在400 K以上,已经接近等容热容的极限值,即杜隆珀蒂极限。
|
| 图 5 Ca5Zn3的(a)体积,(b)体积模量,(c)热膨胀系数和(d)等容热容随温度和压强的变化 Fig. 5 Change of (a) volume, (b) bulk modulus, (c) thermal expansion and (d) heat capacity of Ca5Zn3 with the temperature at various pressures |
3 结论
1) 具有Cr5B3型的Ca5Zn3形成焓最低,是最稳定的结构,与前人的实验结果一致。
2) 弹性常数的计算值显示其满足四方晶系的力学稳定性标准,计算得到了体积模量、剪切模量、杨氏模量以及B/G值,B/G值显示该化合物呈现韧性特征。杨氏模量呈现各向异性。
3) 电子态密度显示Ca的p电子和d电子与Zn的p电子在费米能附近发生杂化效应,费米面上有态密度说明该化合物为金属性。电荷密度差显示Ca失去电子、Zn得到电子,与这两种元素的电负性符合,同时呈现离子键特性。
4) 体积、体积模量、热膨胀系数以及定容热容随着温度和压强的变化趋势说明,随着压强的增加、体积变小,体积模量变大、热膨胀系数变小,定容热容在低温下变小,高温下趋于一致。
| [1] |
BOTTCHER P, DOERT T, DRUSKA C, et al. Investigations on compounds with Cr5B3 and In5Bi3 structure types[J]. Journal of Alloys and Compounds, 1997, 246(1/2): 209-215. |
| [2] |
VENTURINI G, WELTER R. Single crystal refinement of tetragonal Tm3(Ga, Ge)5 with anti-Cr5B3 structure[J]. Journal of Alloys and Compounds, 2000, 299(1/2): L9-L11. |
| [3] |
WU H, ZHOU W, UDOVIC T J, et al. Structural variations and hydrogen storage properties of Ca5Si3 with Cr5B3-type structure[J]. Chemical Physics Letters, 2008, 460(4/5/6): 432-437. |
| [4] |
YUAN F, FORBES S, RAMACHANDRAN K K, et al. Structure and physical properties of Cr5B3-type Ta5Si3 and Ta5Ge3[J]. Journal of Alloys and Compounds, 2015, 650: 712-717. DOI:10.1016/j.jallcom.2015.08.030 |
| [5] |
TAO X M, JUND P, COLINET C, et al. Phase stability and physical properties of Ta5Si3 compounds from first-principles calculations[J]. Physical Review B, 2009, 80: 104103. DOI:10.1103/PhysRevB.80.104103 |
| [6] |
TAO X M, JUND P, COLINET C, et al. First-principles study of the structural, electronic and elastic properties of W5Si3[J]. Intermetallics, 2010, 18(4): 688-693. DOI:10.1016/j.intermet.2009.11.008 |
| [7] |
TAO X M, JUND P, VIENNOIS R, et al. Physical properties of Thallium-Tellurium based thermoelectric compounds using first-principles simulations[J]. The Journal of Physical Chemistry A, 2011, 115(31): 8761-8766. DOI:10.1021/jp204592e |
| [8] |
TAO X M, CHEN H M, TONG X F, et al. Structural, electronic and elastic properties of V5Si3 phases from first-principles calculations[J]. Computational Materials Science, 2012, 53(1): 169-174. |
| [9] |
RITTIRUAM M, HEMATHULIN S, YOKHASING S, et al. First-principles calculation on electron transport properties of Ca-Si[J]. Materials Today-Proceedings, 2018, 5(6): 14052-14056. DOI:10.1016/j.matpr.2018.02.060 |
| [10] |
YANG Z W, SHI D M, WEN B, et al. Structural, elastic, electronic properties and heat of formation of Ca-Zn intermetallics from first-principles calculations[J]. Journal of Alloys and Compounds, 2012, 524: 53-58. DOI:10.1016/j.jallcom.2012.02.075 |
| [11] |
BLÖCHL P E, FÖRST C J, SCHIMPL J. Projector augmented wave method:Ab initio molecular dynamics with full wave functions[J]. Bulletin of Materials Science, 2003, 26(1): 33-41. |
| [12] |
KRESSE G, FURTHMVLLER J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set[J]. Computational Materials Science, 1996, 6(1): 15-50. |
| [13] |
KRESSE G, FURTHMVLLER J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Physical Review B, 1996, 54(16): 11169-11186. DOI:10.1103/PhysRevB.54.11169 |
| [14] |
PERDEW J P, WANG Y. Accurate and simple analytic representation of the electron-gas correlation energy[J]. Physical Review B, 1992, 45(23): 13244-13249. DOI:10.1103/PhysRevB.45.13244 |
| [15] |
CHADI D J. Special points for Brillouin-zone integrations[J]. Physical Review B, 1977, 16(4): 1746-1750. DOI:10.1103/PhysRevB.16.1746 |
| [16] |
FU C L, WANG X D, YE Y Y, et al. Phase stability, bonding mechanism, and elastic constants of Mo5Si3 by first-principles calculation[J]. Intermetallics, 1999, 7(2): 179-184. DOI:10.1016/S0966-9795(98)00018-1 |
| [17] |
PUGH S F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals[J]. The Philosophical Magazine, 1954, 45(367): 823-843. |
| [18] |
BLANCO M A, FRANCISCO E, LUAÑA V. GIBBS:Isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model[J]. Computer Physics Communications, 2004, 158(1): 57-72. DOI:10.1016/j.comphy.2003.12.001 |
| [19] |
陶小马, 陈晨, 郭子凤, 等. RE2Ti3Si4(RE=Gd, Tb, Dy, Ho和Er)物理性质的第一性原理研究[J]. 广西科学, 2014, 21(3): 226-230. DOI:10.13656/j.cnki.gxkx.20140612.004 |
| [20] |
谭旺, 陈贞军, 黄盼宁, 等. B2-CuRE物理性质的第一性原理计算[J]. 广西科学, 2016, 23(2): 174-179. DOI:10.13656/j.cnki.gxkx.20160511.007 |
| [21] |
陶小马, 姚佩, 刘科成, 等. Ta-C化合物物理性质的第一性原理研究[J]. 广西科学, 2017, 24(6): 545-550. DOI:10.13656/j.cnki.gxkx.20171127.001 |



