K近邻(K-nearest Neighbor,KNN)方法由Cover和Hart于1968年提出,使用节点的邻居节点信息构建最近邻图来做分类,是机器学习中常用、简单、易实现的二分类方法。当前,很多数据集具有不均衡性,比如信用卡欺诈、用户违约预测数据集等。这导致KNN方法面临一个挑战:当数据样本不均衡时,KNN方法的预测结果会偏向于样本数占优类。为了提高KNN方法的运行效率、分类效果等性能,很多学者对KNN方法进行了优化。比如沈焱萍等[1]提出基于元优化的KNN方法。王轶凡[2]提出数据时效性的高效KNN方法。王志华等[3]提出基于改进K-modes聚类的KNN方法。张万桢等[4]提出环形过滤器的K值自适应KNN方法。余鹰等[5]使用变精度粗糙集上下近似概念,增强了KNN方法的鲁棒性。樊存佳等[6]采用改进的K-Medoids聚类方法裁剪对KNN分类贡献小的训练样本,提高KNN的分类精度。罗贤锋等[7]使用K-Medoids方法对文本训练集进行聚类,解决了传统KNN方法在文本训练集过大时存在速度慢的问题。针对不均衡数据集,KNN方法预测结果会偏向于样本数占优类的问题,本文将Synthetic Minority Oversampling Technique(SMOTE)[8]和逻辑回归引入KNN方法中,提出了一种基于SMOTE的KNN不均衡样本分类优化方法(A Modified KNN Algorithm based on SMOTE for Classification Imbalanced Data,KSID)。使用SMOTE改进逻辑回归方法或改进KNN方法,虽然可以提高不均衡数据集的查全率,但也会很明显地降低模型查准率;特别是在大数据集上,使用SMOTE会大大增加KNN方法的时间复杂度。因此,本文先使用SMOTE对训练集做上采样,并使用训练过的逻辑回归对该均衡的训练集预测分类,再利用SMOTE和KNN对预测为正样本的数据集做上采样并预测分类,从而训练得到新的KNN模型,以有效地解决SMOTE会降低模型查准率和增加时间复杂度的问题。
1 材料与方法 1.1 逻辑回归逻辑回归通过构建损失函数,并进行优化,迭代,求解出最优的模型参数,最后得到逻辑回归分类模型。其方法如下[9]:
步骤1:随机初始化W和b,利用公式(1)计算预测标签。
| $ Z = {W^T}X + b, $ | (1) |
其中,Z为预测结果,W为权重矩阵,X为特征矩阵,b为偏移量。
步骤2:利用公式(2)计算模型的损失函数。
| $ J(a,b) = \frac{1}{m}\sum\nolimits_{i = 1}^m {L({a^{(i)}},{y^{(i)}})} , $ | (2) |
其中,m为样本数,a(i)为样本i的真实标签,y(i)为样本i的预测标签。
步骤3:利用公式(3)(4)计算W、b的梯度并更新。
| $ {W = W - \alpha \frac{{\partial (J(W,b))}}{{\partial W}},} $ | (3) |
| $ {b = b - \alpha \frac{{\partial (J(W,b))}}{{\partial b}},} $ | (4) |
其中,α为学习率。
步骤4:迭代步骤1到步骤3,直到最小化损失函数J(a, b)。
1.2 KNN方法KNN是一个简单而经典的机器学习分类方法,通过度量待分类样本和已知类别样本之间的距离(一般使用欧氏距离),对样本进行分类。其方法如下[10]:
步骤1:根据公式(5)计算样本点到所有样本点的欧氏距离(d)。
| $ d(x,y) = \sqrt {\sum\limits_{i = 1}^n {{{({y_i} - {x_i})}^2}} } 。$ | (5) |
步骤2:根据欧式距离的大小对样本进行排序(一般是升序)。
步骤3:选取前K个距离最近的邻居样本点。
步骤4:统计K个最近的邻居样本点分别属于每个类别的个数。
步骤5:将K个邻居样本点里出现频率最高的类别,作为该样本点的预测类别。
可以看出,当数据样本不均衡时,KNN方法预测结果会偏向于样本数占优类。
1.3 SMOTESMOTE是常用于样本不均衡数据集的采样方法[8]。其思路是通过合成一些少数类样本,增加少数类样本个数,使得样本均衡。SMOTE的生成策略:对于每个少数类样本x,从它的最近邻样本中随机选一个样本y,然后在x、y属性的欧氏距离之间随机合成新的少数类样本,其工作原理如图 1所示。
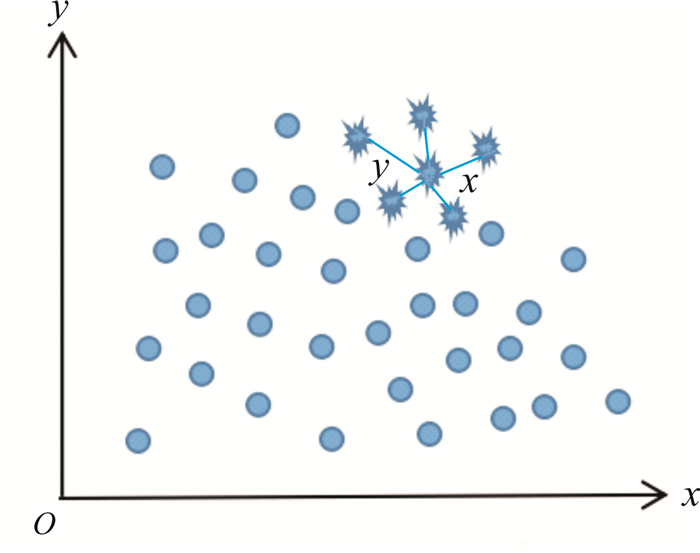
|
| 图 1 SMOTE工作原理 Fig. 1 Working principle of the SMOTE method |
SMOTE的步骤如下[8]:
步骤1:在少数样本集中,对于少数类的样本x,利用公式(5)计算x到其他所有样本的欧氏距离,得到K个最近邻点。
步骤2:通过设置采样比例,得到采样倍率N,并对每一个少数类样本x,从其K近邻中随机选取近邻样本y。
步骤3:对于近邻样本y和样本x,通过计算公式(6),构建新样本。
| $ L = x + {\rm{rand}} (0,1) \times |x - y|, $ | (6) |
其中,x表示少数样本,y表示x的最近邻样本。
1.4 KSID方法将SMOTE和逻辑回归引入KNN方法中,提出了一种基于SMOTE的KNN不均衡样本分类优化方法(KSID)。针对数据样本不均衡对KNN二分类器分类效果影响的问题,使用SMOTE进行采样,增加少数样本的数量,并消除数据样本不均衡对KNN分类效果的影响。KSID方法描述如下:
步骤1:使用SMOTE将不均衡训练集均衡化。将不均衡数据集按照一定的比例划分为训练集和测试集。使用SMOTE对训练集中的每个少数样本,计算其与其他少数样本的欧氏距离,得到K个近邻样本点。通过设置采样比例,随机选取少数类样本,对每一个选出的少数类样本,利用公式(6)构建新样本,一直迭代到训练集的正负样本均衡终止。
步骤2:构建逻辑回归模型。将经过步骤1采样后的训练集放入逻辑回归模型,训练其正则化惩罚项、学习率等参数。并使用训练好的逻辑回归模型,对训练集进行预测。
步骤3:生成KNN模型的训练集并利用SMOTE均衡化。将步骤2中预测为正样本的数据集,作为KNN模型的训练集,并使用SMOTE进行采样,使得训练集的正负样本均衡。
步骤4:构建KNN模型。使用步骤3输出的训练集,训练KNN模型的参数K,并得到模型结果。
步骤5:预测测试集标签。把测试集放入步骤2构建的逻辑回归模型预测,将预测为正样本的数据放入步骤4构建的KNN模型预测,并得到预测结果;最后将KNN模型预测标签与逻辑回归模型预测为负样本的标签合并,得到测试集的预测标签。
算法1给出了KSID算法的形式描述。
算法1:KSID算法
Begin
输入:训练数据x_train, 训练标签y_train,近邻数K,倍率N
输出:新样本类别y_pred
0:将x_train、y_train、K、N传入SMOTE得到数据集newdata
1:将newdata传入逻辑回归方法得到预测结果y_pred
2:y_true=-y_train[y_pred==1]
3:x_true=-x_trian[:, y_pred==1]
4:将x_true、y_true、K、N传入SMOTE得到数据集newdata1
5:将newdata1传入逻辑回归方法得到预测结果y_true_pred
6:y_pred[y_pred==0].append(y_true_pred) #合并结果
7:输出结果y_pred
End
KSID方法虽然将训练集通过SMOTE采样,可以消除数据不均衡性, 但是SMOTE对训练集均衡化后,产生合成的正样本影响分类性能。针对这个问题,将逻辑回归预测的正样本,继续使用KNN进行预测,进而提高分类性能。且KSID方法先使用逻辑回归模型预测出大量正确的负样本,再使用KNN预测少量的正样本,可以有效降低模型计算复杂度,减少模型计算时间。
1.5 实验数据来源本文实验数据集为信用卡欺诈数据集、员工离职数据集、企业诚信数据集、广告点击预测数据集、用户违约数据集、疝气病症预测病马是否死亡数据集,前5个数据集均来源于DC竞赛网(https://www.dcjingsai.com/),第6个数据集来源于百度百科网。数据集的具体描述如表 1所示,其中样本不均衡率计算公式如下[11]:
| $ {\rm{样本不均衡率}} = \frac{{{\rm{正样本数}}}}{{{\rm{负样本数}}}}。$ | (7) |
| 数据集 Data set |
样本 Sample |
变量 Variable |
正样本数 Positive samples |
负样本数 Negative samples |
不均率 Uneven rate (%) |
| 信用卡 Credit card |
284 807 | 29 | 492 | 284 315 | 0.17 |
| 员工离职 Labor turnover |
1 100 | 35 | 178 | 922 | 19.30 |
| 企业诚信 Enterprise integrity |
14 366 | 7 | 941 | 13 425 | 7.00 |
| 广告点击 Click advertising |
1 001 650 | 39 | 198 787 | 802 863 | 24.76 |
| 用户违约 User default |
700 | 12 | 183 | 517 | 35.40 |
| 疝气病症 Colic symptoms |
299 | 21 | 121 | 178 | 68.00 |
1.6 实验环境
使用notebook编译软件、Python 3.6语言编程,分别使用sklearn里的KNN方法、逻辑回归方法和imblearn包中的SMOTE。计算机硬件配置为8 GB内存、64位操作系统、i5-6300HQ处理器。
1.7 实验参数设置训练集和测试集划分比例为7:3,随机种子设置为0;逻辑回归设置fit_intercep为True;SMOTE中的K取值为5,SMOTE采样倍率设置为5;支持向量机(SVM)决策树方法[12]最大深度设置为4;逻辑回归模型和KNN模型都使用3折交叉验证。
1.8 实验方案设计将本文提出的KSID方法分别与逻辑回归方法、KNN方法、SVM决策树方法相比较。基于6个数据集分别测试这4种方法的准确率、精确度、查全率、F1值、运行时间等性能指标,并分析实验结果。
2 结果与分析 2.1 评价指标在机器学习的分类方法中,常常使用准确率来衡量模型的分类效果。但对于不均衡数据集,还需要使用查全率、查准率、F1值等指标评价模型性能。这4种评价指标都是基于表 2的正负样本混淆矩阵。
| 分类 Classification |
预测为正类 Predicted to be positive |
预测为负类 Predicted to be negative |
| 正类 Positive |
TP | FP |
| 负类 Negative |
FN | TN |
其中TP和TN分别表示正确分类的正类和负类的样本数量;FN和FP分别表示错误分类的正类和负类的样本数量。
1) 准确率(Accuracy)
准确率是衡量模型的总体分类效果的指标,准确率越高模型分类效果越好[13]:
| $ \begin{array}{*{20}{l}} {{\rm{Accuracy}}} \end{array} = \frac{{{\rm{TP + TN}}}}{{{\rm{TP + TN + FP + FN}}}} \times 100\% 。$ | (8) |
2) 精确率(Precision)
精确率是模型预测的正样本在真实正样本中所占的比例[11]:
| $ \begin{array}{*{20}{l}} {{\rm{Precision}}} \end{array} = \frac{{{\rm{TP}}}}{{{\rm{TP + FP}}}}。$ | (9) |
3) 查全率(Recall)
查全率指有多少个正样本被模型正确预测为正样本[11]:
| $ \begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{\rm{Recall}}} \end{array}} \end{array} = \frac{{{\rm{TP}}}}{{{\rm{TP + FN}}}}。$ | (10) |
4) F1值(F1 score)
F1值是精确率和查全率的调和值,其结果更接近两者较小的值[11]:
| $ F1 = 2\frac{{\begin{array}{*{20}{l}} {{\rm{Precision \times Recall}}} \end{array}}}{{\begin{array}{*{20}{l}} {{\rm{Precision + Recall}}} \end{array}}}。$ | (11) |
对6个数据集进行准确率测试。从表 3的测试结果可以看出,KSID方法在6个数据集上准确率的均值基本大于其他3种方法,即KSID的分类性优于其他3种方法,特别是员工离职数据集,比KNN方法提高了4.2%。这是因为KSID使用逻辑回归进行第一次分类,再使用KNN对第一次分类预测为正样本的数据进行第二次分类,进而提高了模型的准确率。但对于样本量和特征维度较大的广告点击数据集,KSID方法使用SMOTE采样产生较多的伪样本,影响模型对原始样本的分类准确率,使得KSID方法的分类准确率低于SVM决策树方法。
| 数据集 Data set |
逻辑回归 Logistic regression |
K近邻 KNN |
SVM决策树 SVM decision-making tree |
KSID |
| 信用卡 Credit card |
0.999 2 | 0.999 4 | 0.999 5 | 0.999 5 |
| 员工离职 Labor turnover |
0.861 0 | 0.849 0 | 0.848 0 | 0.891 0 |
| 企业诚信 Enterprise integrity |
0.881 0 | 0.920 0 | 0.930 0 | 0.931 0 |
| 广告点击 Click advertising |
0.681 0 | 0.771 0 | 0.802 0 | 0.780 0 |
| 用户违约 User default |
0.814 0 | 0.781 0 | 0.705 0 | 0.819 0 |
| 疝气病症 Colic symptoms |
0.722 0 | 0.722 0 | 0.744 0 | 0.778 0 |
| 均值 Mean |
0.826 0 | 0.840 0 | 0.838 0 | 0.866 0 |
2.3 精确率测试实验
对6个数据集进行精确率测试,其测试结果如表 4所示。
| 数据集 Data set |
逻辑回归 Logistic regression |
K近邻 KNN |
SVM决策树 SVM decision-making tree |
KSID |
| 信用卡 Credit card |
0.884 | 0.728 | 0.898 | 0.938 |
| 员工离职 Labor turnover |
0.526 | 0.456 | 0.462 | 0.700 |
| 企业诚信 Enterprise integrity |
0.000 | 0.323 | 0.429 | 0.358 |
| 广告点击 Click advertising |
0.000 | 0.305 | 0.671 | 0.362 |
| 用户违约 User default |
0.750 | 0.643 | 0.400 | 0.653 |
| 疝气病症 Colic symptoms |
0.790 | 0.790 | 0.818 | 0.914 |
| 均值 Mean |
0.492 | 0.541 | 0.613 | 0.654 |
从表 4可以看出,KSID方法在6个数据集上精确率的均值基本大于其他3种方法,即KSID模型对正样本预测更准确,如信用卡欺诈数据比KNN方法提升了21%、员工离职数据比KNN方法提高了24.4%等。这是因为KSID使用KNN模型对正样本进行二次分类,进而提高了模型的精确率。但对于企业诚信和广告点击等数据集,由于KSID使用逻辑回归进行第一次分类,而逻辑回归无法识别正样本(其精确率为0),影响了模型的分类精确率,使得KSID方法的分类精确率低于SVM决策树方法。
2.4 查全率测试实验对6个数据集进行查全率测试,从表 5的测试结果可以看出,KSID方法在6个数据集上查全率的均值基本大于其他3种方法,即KSID模型对正样本的召回数量更多,如在信用卡欺诈数据集中,KSID模型的查全率比逻辑回归模型高23.8%、比KNN模型高13.6%等。这是因为KSID使用SMOTE将不均衡数据集均衡化,改进KNN方法对不均衡数据集分类偏向的缺点,进而提高了模型的查全率。但对于员工离职和广告点击等数据集,由于KSID使用KNN对正样本进行二次分类,而KNN对正样本查全率不高,影响了模型的分类查全率,使得KSID方法的分类查全率低于逻辑回归和SVM决策树方法。
| 数据集 Data set |
逻辑回归 Logistic regression |
K近邻 KNN |
SVM决策树 SVM decision-making tree |
KSID |
| 信用卡 Credit card |
0.619 | 0.721 | 0.782 | 0.857 |
| 员工离职 Labor turnover |
0.436 | 0.286 | 0.250 | 0.417 |
| 企业诚信 Enterprise integrity |
0.000 | 0.209 | 0.010 | 0.670 |
| 广告点击 Click advertising |
0.000 | 0.190 | 0.604 | 0.462 |
| 用户违约 User default |
0.444 | 0.333 | 0.300 | 0.593 |
| 疝气病症 Colic symptoms |
0.776 | 0.552 | 0.775 | 0.776 |
| 均值 Mean |
0.379 | 0.382 | 0.454 | 0.629 |
2.5 F1值测试实验
对6种数据集进行F1值测试,从表 6的测试结果可以看出,KSID方法在6个数据集上F1值的均值基本大于其他3种方法,如用户违约数据集KSID模型的F1值比逻辑回归模型高6.4%、比KNN模型高18.3%、比SVM决策树模型高28.2%等。但对于广告点击数据集,由于KSID使用逻辑回归和KNN进行第一、第二次分类,而KNN和逻辑回归对正样本识别率不高(其F1值较低),导致影响了模型的分类F1值,使得KSID方法的分类F1值低于SVM决策树方法。
| 数据集 Data set |
逻辑回归 Logistic regression |
K近邻 KNN |
SVM决策树 SVM decision-making tree |
KSID |
| 信用卡 Credit card |
0.728 | 0.725 | 0.836 | 0.896 |
| 员工离职 Labor turnover |
0.477 | 0.356 | 0.325 | 0.523 |
| 企业诚信 Enterprise integrity |
0.000 | 0.264 | 0.020 | 0.467 |
| 广告点击 Click advertising |
0.000 | 0.249 | 0.636 | 0.406 |
| 用户违约 User default |
0.558 | 0.439 | 0.340 | 0.622 |
| 疝气病症 Colic symptoms |
0.783 | 0.650 | 0.796 | 0.840 |
| 均值 Mean |
0.424 | 0.447 | 0.492 | 0.626 |
2.6 运行时间测试实验
对6种数据集进行运行时间测试,从表 7的测试结果可以看出,对于小数据集,KNN方法的运行时间小,但对于大数据集(比如用卡欺诈数据集),KSID方法时间复杂度明显比KNN方法小得多,如信用卡欺诈数据集KSID运行时间比KNN快266.545 s等。这是因为KSID方法先使用逻辑回归方法预测了量大的负样本,再使用KNN方法预测量少的正样本,进而降低了方法时间复杂度。此外,逻辑回归方法总的运行时间最少,但它在4个预测性能指标上都是最低。KSID既能获得最好的预测性能,也能极大地降低运行时间。
| 数据集 Data set |
逻辑回归 Logistic regression |
K近邻 KNN |
SVM决策树 SVM decision-making tree |
KSID |
| 信用卡 Credit card |
6.734 | 280.113 | 16.058 | 13.568 |
| 员工离职 Labor turnover |
0.138 | 0.020 | 0.073 | 0.209 |
| 企业诚信 Enterprise integrity |
0.146 | 0.153 | 0.150 | 0.243 |
| 广告点击 Click advertising |
16.485 | 193.765 | 144.90 | 34.572 |
| 用户违约 User default |
0.041 | 0.010 | 0.059 | 0.076 |
| 疝气病症 Colic symptoms |
0.022 | 0.004 | 0.021 | 0.037 |
| 合计 Sum |
23.566 | 474.065 | 161.261 | 48.705 |
3 结论
针对KNN方法对样本不均衡数据集的预测偏差问题,本文通过使用SOMTE方法对少数样本类的训练集进行采样操作,使得训练集的正负样本数量保持基本一致,从而改善了不均衡数据对KNN模型预测性能的影响。对比实验结果发现,基于SMOTE改进后的KSID方法,比逻辑回归方法、原始KNN方法、SVM决策树方法的分类效果更优,对于较大数据集其时间复杂度更小。但对于样本量和特征维度较大的数据集(如广告点击数据集),KSID方法使用SMOTE采样会产生较多的伪样本,导致影响了模型对原始样本的分类性能,使得KSID方法的分类性能低于SVM决策树方法。
| [1] |
沈焱萍, 伍淳华, 罗捷, 等. 基于元优化的KNN入侵检测模型[J]. 北京工业大学学报, 2020, 46(1): 24-32. |
| [2] |
王轶凡. 考虑数据时效性的高效KNN方法[J]. 赤峰学院学报:自然科学版, 2019, 35(11): 19-21. |
| [3] |
王志华, 刘绍廷, 罗齐. 基于改进K-modes聚类的KNN分类方法[J]. 计算机工程与设计, 2019, 40(8): 2228-2234. |
| [4] |
张万桢, 刘同来, 邬满, 等. 使用环形过滤器的K值自适应KNN方法[J]. 计算机工程与应用, 2019, 55(23): 45-52, 85. |
| [5] |
余鹰, 苗夺谦, 刘财辉, 等. 基于变精度粗糙集的KNN分类改进方法[J]. 模式识别与人工智能, 2012, 25(4): 617-623. |
| [6] |
樊存佳, 汪友生, 边航. 一种改进的KNN文本分类方法[J]. 国外电子测量技术, 2015, 34(12): 39-43. |
| [7] |
罗贤锋, 祝胜林, 陈泽健, 等. 基于K-Medoids聚类的改进KNN文本分类方法[J]. 计算机工程与设计, 2014, 35(11): 3864-3867, 3937. |
| [8] |
BLAGUS R, LUSA L. SMOTE for high-dimensional class-imbalanced data[J]. BMC Bioinformatics, 2013, 14(1): 106. |
| [9] |
张士翔, 李汪根, 李童, 等. 一种改进的贝叶斯逻辑回归核心集构建方法[J]. 计算机科学, 2019, 46(S2): 98-102. |
| [10] |
刘淑英, 邹燕飞, 李依桥, 等. 基于KNN方法的约会网站配对模型的应用研究[J]. 数字技术与应用, 2019, 37(10): 128-129. |
| [11] |
钟龙申, 高学军, 王振友. 一种新的基于K-means改进SMOTE方法在不平衡数据集分类中的应用[J]. 数学的实践与认识, 2015, 45(19): 198-206. |
| [12] |
黄勇, 魏乐. 一种针对不均衡数据集的SVM决策树方法[J]. 成都信息工程大学学报, 2019, 34(3): 274-277. |
| [13] |
GOIN J E. Classification bias of the k-nearest neighbor algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, 6(3): 379-381. |



