2. 广西高校并行与分布式计算技术重点实验室, 广西南宁 530004
2. Guangxi Colleges and Universities Key Laboratory of Parallel and Distributed Computing Technology, Nanning, Guangxi, 530004, China
近年来,随着数据采集设备的普及,以传感器网络[1]、金融服务[2]、网络监控[3]、航空航天以及气候监测为代表的重要应用源源不断地产生数据流,这些数据流亟待分析处理。数据流的产生具有无限性、连续性和快速性,因此数据流的分析处理要求及时性,以保证分析结果的时效性。一条数据流S可以形式化表示为S={s1, s2, s3, …, si, …},其中si表示第i个到达后端分析处理系统的流元组,si.v表示该流元组的值,si.ts表示该流元组的产生时间,称为该流元组的时间戳。对数据流的分析处理,通常是基于流元组的时间戳语义进行的。例如,手机导航跟踪用户移动设备地理位置数据流,就是基于时间顺序的最新元组信息,给用户实时推荐行进的路线。但是,由于网络延迟、处理器的并行操作或是异步数据流合并等原因[4],使得数据流上流元组不能按其时间戳的先后顺序到达后端分析处理系统,导致数据流出现乱序现象。例如在高速公路上,当手机导航上传数据中心的数据流出现乱序现象时,定位信息会大量遗漏丢失,产生异常跳动的现象,破坏了连接结果的完整性,影响了实时推荐的路线引导建议的准确性。
为了减少乱序的影响,提升连接结果完整性,人们提出了基于缓存的乱序数据流处理方法,即缓存一定已到达的流元组,等待迟来的流元组,换取结果质量的提升。其中,Abadi等[5]提出的K-slack方法就是基于缓存的乱序数据流处理方法的典型代表。该方法通常用一个大小为K时间单位的缓存来存储已到达的流元组,即每个流元组到达系统后还需等待K个时间单位才能被释放以继续处理,释放按缓存内流元组的时间戳从小至大依次进行。在K-slack方法中,到达的流元组需等待K个时间单位后才被分析处理,有效避免了延迟时间小于K个时间单位的迟到元组对结果质量带来的负面影响,但仍然会丢失延迟时间大于K个时间单位的迟到元组的连接结果。之后,Babu等[6]和Mutschler等[7]进一步改进了K-slack方法,使缓存区参数K随数据流延迟大小变化进行动态调整,直到K值等于当前最大的延迟,从而优化了缓存的大小,降低了对迟到流元组的平均等待时间,提高了连接处理的执行效率。近年,Ji等[8-10]基于用户指定的结果质量指标优化参数K的取值:将连接结果质量定义为连接结果集的召回率,给定用户指定的结果质量指标,基于连接处理过程中收集的统计数据优化和调整参数K的取值。由于参数K和流元组到达系统后的等待时间相关,该方法在保证结果质量指标前提下尽可能降低了对迟到流元组的平均等待时间。上述方法虽然保证了连接结果在时间域上的有序性,但还是增大了流元组的连接处理时延。杨宁等[11]研究设计一种混合嵌入分布式流处理模块和分布式批处理模块的乱序数据流分布式聚合查询处理技术,该技术通过限制自适应地优化流处理模块所用的缓冲区大小来降低流处理的查询处理延迟;利用存储的历史流数据,以批处理的方式实现对极其晚到流元组的查询处理,进而保障聚合查询结果的最终正确性。
除了K-slack方法以外,人们在数据流乱序处理方法中还运用了基于标点元组的方法和基于推测的方法。基于标点元组的方法是在数据流中插入标志时间进度的标点元组,标点元组后到来的流元组时间戳都比标点元组时间戳大,以此避免错过对一些迟到元组的处理。例如,心跳机制[12]以及部分有序保证机制[13-14]都是基于标点元组的方法。Mencagli等[15]以多核系统为背景,研究解决乱序流式大数据上的连续偏好查询(例如Top-k查询和Skyline查询)的并行执行问题,采用基于K-slack的缓存技术产生标点元组,并基于标点元组确定乱序数据流发送进度。在基于标点元组的方法中,如果标点元组迟迟不到,那么可能会使得窗口等待闭合的时间延长,不利于实时性要求较高的连接处理操作,严重影响查询处理的效率。基于推测的方法是一种激进的处理方法[16-17],该方法以假设数据流元组是有序到达的为前提,先激进地处理已到达系统的流元组,输出处理结果,直到后续迟到流元组的到来。仅当确认之前输出结果不正确时,该方法才进行结果撤回,利用存储的历史数据重新计算和输出结果。基于推测的方法加快了乱序数据流的处理效率,常用于处理乱序事件流,实现对复合事件的实时检测,但由于需存储大量的历史数据,增大了内存开销,且迟到元组频繁出现可能导致错误结果连续撤回,增大连接开销。
一些研究人员从时间维度、外形轮廓和结构变化上的相似性等3个角度,对基于时间关联性的数据流相似性进行研究。Aghabozorgi等[18]利用大量数据流的统计量对数据流进行宏观上的比对,聚类比较了数据流的不同阶段或不同的数据流之间相似性。Mukhoti等[19]对数据流提取模糊关联模式用以预测事件。Jacques-Silva等[20]讨论了Facebook如何基于历史数据构建分布式计算环境下乱序流式大数据的流元组延迟估计模型,并基于该估计模型和用户对系统处理单元的处理延迟的需求生成一定精度的标点元组,从而权衡单处理单元的处理延迟和连接查询的结果精度这两个重要指标。朱睿等[21]针对数据流上的连续Top-k查询设计了哈希过滤器,可以有效过滤不可能成为查询结果的乱序流元组,从而降低对乱序流元组的等待时间。许嘉等[22]提出了一种基于EMD距离的数据流分布式相似性连接技术(EMD-DDSJ),该技术基于数据局部性特征增强了连接算法对不相似直方图元组对间EMD计算的过滤性能,提高了各连接计算节点的执行效率;通过一种基于反馈的负载均衡策略,有效提升EMD-DDSJ技术的整体执行性能。
为了降低乱序数据流的平均连接处理时延,满足用户及时性需求[23],本研究提出了质量驱动的乱序数据流连接处理技术(简称QJoin)。该技术将通过缓存一定量的历史数据并采用对称连接的策略实现对到达系统流元组的即时处理并输出连接结果,以期显著降低流元组的平均处理时延,提高连接处理的速率;基于用户指定的结果质量指标来优化内存使用量,降低平均内存开销。最后,基于真实数据集对QJoin技术进行实验验证,以说明该技术的有效性。
1 方法描述 1.1 QJoin的设计思想在数据流的连接操作中,用户非常关注处理的实时性和准确性,因此必须考虑数据流乱序问题的处理。在处理数据流乱序问题上,基于缓存的方法是最常见的处理方法之一。经研究分析,现有的基于缓存处理乱序方法多以最优结果完整性或最优处理效率为目的,以数据流的整个历史的最大延迟或者平均延迟作为参考,对缓存大小进行调整,没有考虑数据流的时间关联性,忽略了临近时间段的延迟变化对缓存的影响。现有的方法很少从用户的角度来综合考虑结果完整性、存储开销、处理效率的有效折中,使得晚到的元组到来后不能即时进行连接处理,增加了数据流平均连接处理时延,导致处理效率不高。
针对以上问题,本研究提出了一种基于质量驱动的乱序数据流连接处理技术QJoin的框架(图 1)。QJoin的设计思想:关注数据流的及时性处理需求,特别是晚到数据流的连接与调度,将基于缓存的方法和对称连接方法[24]有机结合起来,实现对乱序数据流流元组的即时处理。其技术特点在于:综合权衡了用户结果质量与缓存开销,考虑了数据流上的时间关联性,基于临近周期连接处理过程收集统计的数据,优化缓存的大小,更好地实现对数据流的及时性处理。

|
| 图 1 QJoin的技术框架 Fig. 1 Technique framework of QJoin |
QJoin采取了以下的技术处理手段:
(1) 每条数据流的流元组到达系统后,进入存储流实现在内存中的缓存,同时进入连接流实现和另一条数据流在内存中缓存元组之间的连接处理。以图 1中乱序流R的元组ri(i=1, 2, …)为例,当ri到来时,同时进行两个工作:一是进入存储流完成在流R缓存中的存储;二是进入连接流实现和数据流S缓存元组之间的连接处理,直到生成结果流,从连接流中丢弃。乱序流S的元组sj(j=1, 2, …)到来时,操作是类似的。
(2) 存储流和连接流对于每个流元组的处理都是即时的。每条流在内存中的缓存都运行一定的过期清理策略,从缓存中删除过期的流元组。
(3) 在进行对称连接处理的过程中,QJoin技术不断基于临近的周期的历史元组计算用户指定质量指标,收集统计信息进行估计结果质量,统计信息包括如图 1中各元组延迟和生产力、各周期结果数目,在满足用户指定的结果质量的同时,尽可能降低对历史数据的内存缓存量,从而优化缓存的大小。
1.2 对称连接方法QJoin技术采用对称连接的方式处理乱序数据流连接,同时缓存一定量的历史数据。假设缓存区大小设定为可以容纳住所有需要连接的元组,具体的处理步骤如下:
Step 1:流元组r∈R到达系统后,由存储流实现在内存中的流R缓存区的存储,同时由连接流即刻完成r和流S缓存区中落在滑动窗口内的流元组的连接,输出连接结果,连接流上的元组r丢弃;
Step 2:对于到达系统的流元组s∈S,同样由连接流即刻完成s和对面流R缓存区中落在滑动窗口内的流元组的连接,输出连接结果,连接流上的元组s丢弃;
Step 3:流R缓存区和流S缓存区中,当元组数目超出缓存区的大小就会被移出缓存区,进行丢弃。
数据流的延迟定义为当前流上到来的最大时间戳与迟到元组时间戳的差,QJoin利用延迟统计量d,定时将流R缓存区和流S缓存区中满足x.ts≤T-d的流元组清除,其中x为R流或S流的流元组,T为R流和S流上最大时间戳中的最小值,标记为当前时刻。QJoin技术在对称连接方法的基础上,考虑到流上延迟分布与待连接流缓存的关系,元组延迟与结果质量存在关联性,满足用户指定结果质量的同时,自适应调整元组过期,优化内存使用量。
由于在对称连接中,只要连接流上元组到来就可以与对面的缓存内元组即时连接,所以即使是因存在乱序问题而导致元组迟到的现象,只要其待连接的元组还在对面缓存区中,就可以有效地完成连接操作,保证了处理的及时性和结果的完整性。因此,缓存区的大小设定受到对面连接流上迟到元组的影响,需要储存这些迟到元组待连接的元组。
1.3 乱序数据流连接结果质量QJoin技术中,使用结果召回率作为处理乱序数据流的质量标准。结果召回率是实际连接得到的结果数目占本应该连接得到的理想结果数目的百分比[25]。QJoin技术考虑用户对连接处理结果的及时性需求,允许用户指定一个用户周期P,以P周期的结果召回率来替代整个流历史的结果召回率。同时,由于数据流元组间的时间关联性,用最新的P周期历史来计算结果召回率,可敏锐地捕捉到结果召回率的变化,以帮助后续的乱序流处理操作得到更好的结果质量。
在QJoin中,假设用户给定了周期P,则周期P内实际的流连接质量为召回率QP:
| $ {Q_P} = \frac{{{N^\prime }_P}}{{{N_P}}}, $ | (1) |
其中,N′P为在最近的P周期内结果数目,NP为最近的P周期内理想情形应该得到的结果数目。
QJoin中用户可以指定结果质量(召回率),表示为Quser,要求P周期内求得的召回率QP满足:QP≥Quser。
1.4 基于用户质量的缓存自适应 1.4.1 缓存自适应调整在QJoin中,需要缓存足够大,能包含窗口内所有应到来的元组时,必须考虑到延迟元组的影响:需缓存的元组包括落在窗内的元组和窗外的迟到元组,即缓存大小与窗内元组和元组延迟分布有关。QJoin技术在用户指定质量要求下,自适应调整缓存大小,方法如下:使用一个大小为周期P的大滑动窗口,滑动步长为自适应周期L,从流上第一个P周期结束时刻起,利用最近的L周期历史元组特性,进行下一个L周期的缓存估计设置,即当大窗口每滑动一次,前进L周期,基于最近的L周期历史进行一次缓存自适应调整,要求L < P。
在每一次缓存自适应调整中,需要满足目标函数。设R流与S流的占用的缓存分别为x、y,求出对应的(x, y),使流占用的总缓存M(x, y)尽可能小的目标函数如下:
| $ \begin{array}{l} {\rm{min}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} M(x,y) = x + y,\\ s.t.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {Q_L}(x,y) \ge {Q_L},\\ 0 \le x \le X,\\ 0 \le y \le Y, \end{array} $ | (2) |
其中,M(x, y)为总缓存大小,是R流缓存大小x与S流缓存大小y的和。当数据流的流速一定时,x与y受存放时间的影响。存放时间就是元组过期前在缓存中的时间,决定元组何时过期移出内存,受元组的延迟d与窗口w大小影响。当窗口大小固定,存放时间的变动只受元组的延迟影响,保存时间增加d时间单位时,延迟为d的元组就可进入存储流参与连接,因此设流R的流速为Vr,缓存x与R流延迟dx的关系可以表示为x=(dx+w)×Vr,同理,流S的流速为Vs,缓存y与S流延迟dy的关系可以表示为y=(dy+w)×Vs,缓存问题可以转化为时间问题。
QL(x, y)为最近L周期历史下,R流缓存大小设置为x与S流缓存大小设置为y时的结果质量,QL为基于P周期内用户要求质量求得的L周期的质量期望(具体求解见1.4.2),X为受R流当前最大延迟与窗口大小影响的最大缓存,Y为S流受当前最大延迟与窗口影响的最大缓存。
1.4.2 L周期用户质量期望L周期的用户质量期望,是基于P周期内召回率QP需要满足的条件QP≥Quser求出的,其中Quser就是用户指定的结果质量,这里只需要求取QP的值。由公式(1)可知,求QP需要知道两个参数:在当前时刻最近的P周期内结果数目N′P,以及当前时刻最近的P周期内理想情形应该得到的结果数目NP。N′P的求解是将P周期分为两段来求:P周期内除了最近L周期历史后余下的P-L段和L段。通过实际统计得到P-L段实际结果数目N′P-L;通过统计信息估计L时间段实际结果数目,即由理想情形应该产生的结果数NL和L阶段内用户质量期望QL的积来替代。因此,条件中的QP召回率可以替换为如下形式:
| $ \frac{{{N^\prime }_{P - L} + {N_L} \times {Q_L}}}{{{N_P}}} \ge {Q_{user}}。$ | (3) |
L阶段内用户质量期望QL可由式(3)求出,其中,N′P-L表示P周期内除去最近的L周期历史后余下的实际结果数;NL和NP分别表示自适应周期L和周期P理想情形应该产生的结果数。这里认为NL与NP是成比例的,满足NL/NP=L/P,因此NP和NL可只求两者之一即可,具体见下一小节。
1.4.3 L周期受缓存影响的质量QL(x, y)当数据流的流速V一定时,L阶段受缓存容量影响的实际质量QL(x, y)转化为受R流延迟dx与S流延迟dy影响的质量QL(dx, dy):
| $ {Q_L}({d_x},{d_y}) = \frac{{{N_{prod}}({d_x},{d_y})}}{{{N_L}}}, $ | (4) |
其中,Nprod(dx, dy)为L阶段内受R流延迟dx与S流延迟dy影响产生的结果数目,NL为L周期理想状态应该产生的结果数目。Nprod(dx, dy)受到选择度sel(dx, dy)与交叉连接的结果数N×(dx, dy)的影响,计算公式为
| $ {N_{prod}}({d_x},{d_y}) = sel ({d_x},{d_y}) \times {N_ \times }({d_x},{d_y})。$ | (5) |
下面分别给出L阶段内交叉连接数Nx(dx, dy),选择度sel(dx, dy)的求解过程。
1) Nx(dx, dy)的求解
L时间段交叉连接数目,是L时间段内到来的R流元组与其对应的S流窗内所有元组的连接数Nx(dy)和此时S流元组与其对应的R流窗内元组的连接数Nx(dx)的和。交叉连接数Nx(dx)的求解方式与交叉连接数Nx(dy)的求解方式类似,这里以流R的交叉连接数Nx(dx)求解为例。
设窗口大小为w,对于任意输入元组r∈R,只有对应的S流元组s满足|r.ts-s.ts|≤w时,才能进行连接,则对元组r而言,其交叉连接数是S流窗内元组数目|W′s|。因此L周期内,若已知数据流R的平均流速Vr,可求输入的R流元组数目,对每个R流元组对应的S流窗内元组数,可求出流R的L阶段交叉连接数Nx(dy):
| $ {N_ \times }({d_y}) = {V_r} \times L \times |{W^\prime }s|, $ | (6) |
其中,|W′s|受延迟dy影响,由实际情况可知,缓存越大,窗口内迟到元组被连接上的数目越多,然而缓存中输入流元组越新的地方,元组迟到的可能性越大,因此通过对窗口w进一步切割,设置基础窗b[21]来计算受迟到元组影响的窗口内元组数目。
为了更清晰地描述迟到元组对窗口内元组的影响,需先求出迟到元组t的延迟分布特性。设随机变量D表示元组粗粒度的延迟,g表示实际的延迟粒度,当delay(t)∈[0, g],令D=0;当delay(t)∈(g, 2g],令D=1;当delay(t)∈(2g, 3g],令D=2;余下的依次类推。设fD(d)为随机变量D的概率密度,表示为fD(d)=P[D=d],d=1,2,3,…,是延迟为D=d的元组出现的概率。设基础窗大小为b时间单位,将大小为w的窗口被分成n个小窗口,以S流窗举例,S流窗内元组数目相当于n个小窗口内元组数目的和,每个小窗口的元组数目W′s是由平均流速VS和基础窗大小b及落入到基础窗的元组概率的积决定的,计算公式如下:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} W{s^\prime } = \sum\limits_{i = 1}^n {|{{\tilde \omega }_i}|} = \sum\limits_{i = 1}^{n - 1} {Vs \times b} \times \sum\nolimits_{d = 0}^{\frac{{i - 1}}{b}} {{f_D}(d)} + \\ Vs \times [w + {d_y} - (n - 1)b] \times \sum\nolimits_{d = 0}^{\frac{{n - 1}}{b}} {{f_D}(d)} 。\end{array} $ | (7) |
L周期的本来应该产生的结果数NL同样是选择度sel与交叉连接数N×的积,计算公式如下:
| $ {N_L} = {\rm{sel}} \times {N_ \times }, $ | (8) |
其中,交叉连接数N×表示在最理想状态,当缓存能包含所有迟到元组的情形下,可能得到的交叉连接数N×,选择度sel同样放在后面讲具体细节。对L阶段内交叉连接结果数N×:
| $ {N_ \times } = {N_ \times }( Max{d_x}) + {N_ \times }( Max{d_y}), $ | (9) |
其中,Maxdx表示为在R流上最大的延迟,Maxdy表示为S流上最大的延迟,N×(Maxdy)和N×(Maxdx)分别是理想状态下R流与S流交叉连接数目,求解方式类似。以流R的交叉连接数目N×(Maxdy)为例,设窗口大小为w,若已知数据流R的平均流速Vr,可求出在L周期输入的R流元组数目,每个R流元组对应的S流窗内元组数在理想状态下包括所有实际落在当前窗口内的元组与迟到元组,因此L阶段内流R的交叉连接数目N×(Maxdy)表示为
| $ {N_ \times }(Max{d_y}) = {V_s} \times L \times {V_r} \times (\tau \omega + Max{d_y})。$ | (10) |
2) sel(dx, dy)的求解
选择度是符合相似度函数的实际连接次数占所有参与连接的实际连接次数的百分比,基于最近的L周期内延迟与元组产出结果的关系来求得。在最近L周期内,当元组t输入时,统计延迟delay(t),元组的连接数N′(t)和元组的结果数N(t)。受延迟dx和dy影响的最近L阶段的选择度计算如下:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} sel ({d_x},{d_y}) = \\ \frac{{\sum\nolimits_{d = 0}^{{d_y}} {\sum\nolimits_{delay(r) = d} {{N^\prime }(r)} } + \sum\nolimits_{d = 0}^{{d_x}} {\sum\nolimits_{delay(s) = d} {{N^\prime }(s)} } }}{{\sum\nolimits_{d = 0}^{{d_y}} {\sum\nolimits_{delay(r) = d} {N(r)} } + \sum\nolimits_{d = 0}^{{d_x}} {\sum\nolimits_{delay(s) = d} {N(s)} } }}。\end{array} $ | (11) |
同理,理想状态下的选择度可认为是受最大延迟的影响,最近L阶段的理想选择度计算如下:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} sel (Max{d_x},Max{d_y}) = \\ \frac{{\sum\nolimits_{d = 0}^{Max{d_y}} {\sum\nolimits_{delay(r) = d} {{N^\prime }(r)} } + \sum\nolimits_{d = 0}^{Max{d_x}} {\sum\nolimits_{delay(s) = d} {{N^\prime }(s)} } }}{{\sum\nolimits_{d = 0}^{Max{d_y}} {\sum\nolimits_{delay(r) = d} {N(r)} } + \sum\nolimits_{d = 0}^{Max{d_x}} {\sum\nolimits_{delay(s) = d} {N(s)} } }}。\end{array} $ | (12) |
假设有两条乱序数据流R和S,QJoin技术中缓存自适应调整的伪代码为
算法1 QJoin技术中的缓存自适应调整算法
输入:自适应间隔L、基础窗口大小b、窗口大小w、延迟增加的粒度g、相似函数的阈值θ、流R中当前最大延迟流Maxdx、流S中当前最大延迟Maxdy、每个元组的连接数目、每个元组的连接结果数目、每个P-L周期实际连接结果数目、从用户指定质量Quser得到的L周期质量期望QL、流R的流速Vr、流S的流速Vs
输出:(x, y),其中x表示R缓存大小,y表示S缓存大小
Begin
1 dx=0; dy=0; //对元组延迟的初始化
2 while (dy < =Maxdy) do //将延迟查找范围限制在当前历史流上最大延迟内
3 while (dx < =Maxdx) do
4 if (QL(dx, dy) < QL) dx=dx+g;
5 else record(dx, dy);
6 dy=dy+g;
7 for each (dx, dy) in record(dx, dy) do
8 x=(dx+w) *Vr; //计算缓存的总使用量
9 y=(dy+w) *Vs;
10 M(x, y)=x+y;
11 if (getMin(M(x, y)) //比较所有记录值
12 return (x, y);
End.
在上述算法中,每个自适应周期结束后对缓存进行一次调整,其中1-6行是利用延迟特性与质量的关系,求出所有可以满足L周期质量期望的需要缓存元组的延迟。如果缓存了小于等于该延迟值的元组后得到的结果质量满足L周期的质量预期QL,就记录下来,否则就增大一个g延迟粒度。第7-12行是利用延迟与缓存的关系,返回适宜的缓存。通过比较计算得到的所有记录值,求出使总缓存值最小的R流缓存x,S流缓存y。QJoin技术中,考虑了缓存的最理想情况,即延迟最大的元组都可以在缓存中找到所有需要连接的元组,这时得到的召回率是L周期内理想情况召回率;此外,还考虑了最近L周期召回率与缓存之间关系,使用用户质量指标和统计量采样,得到更合理的缓存,以降低缓存开销。
2 结果与分析 2.1 实验环境设置本实验使用一台CPU 3.1 GHz、16 G内存、500 G硬盘的PC设备进行试验测试。操作系统是Windows 10,所有代码用Java语言编写。实验数据集包括2段球赛训练数据D1和D2,源于一场足球比赛数据[1],由德国纽伦堡体育足球场上的传感器系统采集。该数据包含两条数据流(R流和S流),分别由足球上的传感器和运动员身上的传感器采集。数据集中每个元组包含信息(sID, ts, location),其中sID用于区分R流和S流,ts表示元组时间戳,location是运动员们在球场的位置信息。具体信息如表 1。
| 数据Data | 数据集特征Data set characteristics | |||||
| 总时间长度Total time length (s) | 总元组数目Total number of tuples | 元组到来速度Tuple arrival speed (tuples/s) | 迟到元组数目Number of late tuples | 最大延迟Maximum delay (s) | 平均延迟Average delay (ms) | |
| D1 | 831.174 201(约13.86 min)(Approximately 13.86 min) | 7 122 060 | 8 514 | 5 940 703 | 142.146 64 | 34.133 |
| D2 | 384.084 109(约6.41 min) (Approximately 6, 41 min) | 4 022 600 | 10 037 | 3 493 068 | 170.959 26 | 29.597 |
本实验使用的查询语句为
SELECT * FROMR[2 sec], S[2 sec] WHERE distance(R.location, S.location) < =5 m。
重要参数默认设置值包括用户指定质量周期P=1 min,自适应调整周期为L=1 sec,基础窗口大小为b=10 ms,自适应调整粒度为g=10 ms。
2.2 参数设置对内存开销的影响为了使结果显示更清晰明确,实验中使用连接过程中平均内存开销作为度量标准。当数据流流速一定时,平均内存开销越大,可存储的迟到元组延迟就越大。
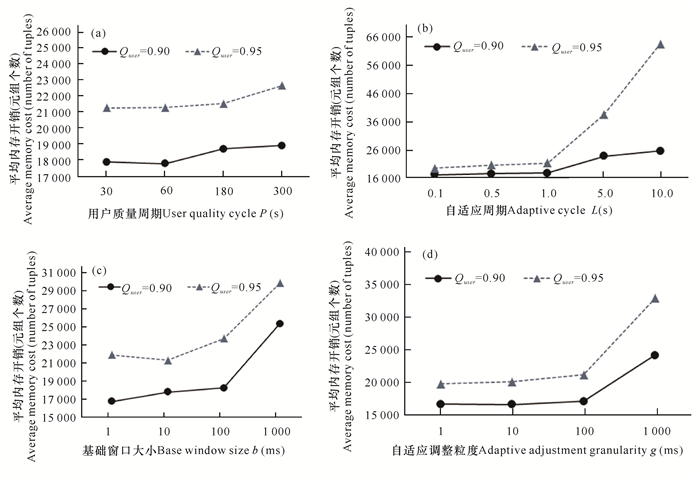
首先考察QJoin技术中重要参数设置对内存开销的影响。为此,分别对用户指定质量周期P、自适应调整周期L、基础窗口大小b、自适应调整粒度g进行设定值调整来进行比较实验,其他条件为默认设置值。图 2为用户指定最小召回率为Quser=0.90和Quser=0.95,使用数据集合D1时,重要参数设置对算法影响的实验结果。实验中使用平均内存开销(即缓存的元组数目)来显示实验的结果。图 2a中观察到周期P对内存的平均开销影响并不大,只是在周期P设置为60 s,显示微小的差异,因此最终周期P默认设置为60 s。图 2b可以清晰显示出当自适应周期为0.1 s时平均内存开销更少,实际应用时可以设置自适应周期L为0.1 s。由图 2c中观察到基础窗大小b的选取过于细小或者宽大,都会使估计不够准确,或平均内存开销增大。由图 2d可观察到当自适应调整粒度g取10 ms时,平均内存开销较低。
|
| 图 2 不同参数对QJoin技术平均内存开销的影响 Fig. 2 Effect of different parameters on the average memory cost of QJoin technology |
2.3 QJoin技术和MP- K- slack技术性能比较
由于MP-K-slack[7]技术具有典型性,通常被作为相关技术研究的实验比较对象,因此本研究也是将QJoin技术和MP-K-slack技术进行比较。
1) 流元组平均处理时延比较
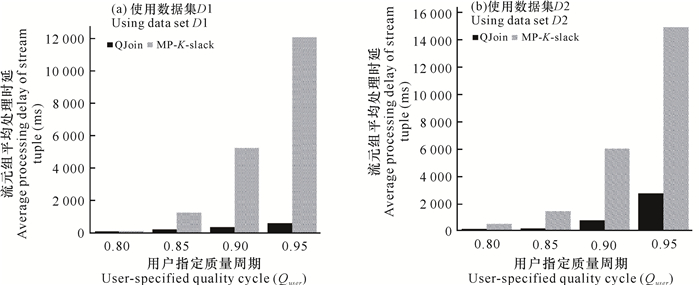
流元组平均处理时延是所有元组进入系统到最终输出连接结果的时间间隔平均值。图 3给出了QJoin技术和MP-K-slack技术关于流元组平均处理时延的实验对比结果。
|
| 图 3 QJoin技术和MP-K-slack技术的流元组平均处理时延比较 Fig. 3 Comparision of average tuple processing delay of algorithms QJoin and MP-K-Slack |
MP-K-slack技术的处理思路是设置一个K时间单位的缓存,初始值为0,当前流历史上最大时间戳标注为当前时刻tcurr,每到来一个元组就插入到缓存中,与当前时刻tcurr比较,若大于tcurr,就更新tcurr。当tcurr更新时,做如下两个操作:1)更新K=max{K, D(x)},其中D(x)=tcurr-x.ts,是元组x的延迟,是上一次tcurr更新时计算得到的;2)将满足x.ts+K < =tcurr的元组,从缓存中弹出。从工作原理来看,MP-K-slack技术随延迟分布波动,始终以当前最大延迟作为等待时间,正常元组需要等待较长时间后才能释放进行连接处理,流元组平均处理时延较长。而本研究提出的QJoin技术中,元组一旦进入系统就开始连接,并快速输出结果。当用户要求的召回率超过0.85时,相比于MP-K-slack技术,QJoin技术的流元组处理时延降低了约80%-95%(图 3),原因是MP-K-slack技术必须要缓存元组更久,才能有效处理尽可能多的迟到元组,满足召回率,而QJoin技术在对称连接和合理缓存的情形下可以直接参与连接,可以更快地进行流元组的连接,有利于提高系统进行连接处理的处理速率。
2) 平均内存开销比较
与MP-K-slack技术相比,在用户要求召回率越高的情况下,本研究提出的QJoin技术平均内存的开销较低,存储使用量明显降低了约50%-80%(图 4)。原因在于:MP-K-slack技术为了满足足够的召回率,必须要缓存阻塞元组更久,就会使更多的元组滞留在缓存区中,特别是在流速较快、延迟较大的迟到元组较多的数据流中(图 4a),而QJoin技术是基于对称连接的技术,在满足召回率的情形下只需要合理缓存适量的历史元组,因此优化效果明显,对内存的需求更低。

|
| 图 4 QJoin技术和MP-K-slack技术平均内存开销比较 Fig. 4 Comparison of average memory cost between QJoin and MP-K-Slack |
3 结论
本文研究了质量驱动下的乱序数据流连接处理问题,提出一种质量驱动的乱序数据流连接处理技术QJoin。该技术基于数缓存和对称连接方法实现对乱序数据流流元组的即时处理,显著降低了流元组的平均等待时延,提升了基于滑动窗口语义的乱序数据流连接处理的处理速率。采用质量驱动的理念,基于连接处理过程中收集的统计数据优化缓存的大小,使得在满足用户指定的结果质量的同时,大大降低了对历史数据的内存缓存量;利用历史数据元组缓存,较好地保证了迟到元组的连接处理完整性,从而实现在满足用户结果质量要求的前提下尽可能降低了系统内存开销。与现有的MP-K-slack方法相比,QJoin技术在满足用户结果质量的同时,不仅能够保证较低的数据流流元组处理时延,比MP-K-slack方法最大降低了约95%,还有效降低了内存使用开销,比MP-K-slack方法最大降低了约80%。
| [1] |
MUTSCHLER C, ZIEKOW H, JERZAK Z.The DEBS 2013 grand challenge[C]//ACM.The 7th ACM International Conference on Distributed Event-Based Systems.ACM, Arlington, Texas, USA, 2013: 289-294.
|
| [2] |
GU X W, ANGELOV P P, ALI A M, et al.Online evolving fuzzy rule-based prediction model for high frequency trading financial data stream[C]//IEEE.2016 IEEE Conference on Evolving and Adaptive Intelligent Systems.IEEE, Natal, Brazil, 2016: 169-175.
|
| [3] |
ACETO G, BOTTA A, PESCAPE A, et al. Efficient storage and processing of high-volume network monitoring data[J]. IEEE Transactions on Network and Service Management, 2013, 10(2): 162-175. DOI:10.1109/TNSM.2013.011713.110215 |
| [4] |
MENCAGLI G, TORQUATI M, DANELUTTO M, et al. Parallel continuous preference queries over out-of-order and bursty data streams[J]. IEEE Transactions on Parallel and Distributed Systems, 2017, 28(9): 2608-2624. DOI:10.1109/TPDS.2017.2679197 |
| [5] |
ABADI D J, CARNEY D, CETINTEMEL U, et al. Aurora:A new model and architecture for data stream management[J]. The VLDB Journal, 2003, 12(2): 120-139. DOI:10.1007/s00778-003-0095-z |
| [6] |
BABU S, SRIVASTAVA U, WIDOM J. Exploiting kco-nstraints to reduce memory overhead in continuous queries over data streams[J]. ACM Transactions on Database Systems, 2004, 29(3): 545-580. |
| [7] |
MUTSCHLER C, PHILIPPSEN M.Distributed low-latency out-of-order event processing for high data rate sensor streams[C]//IEEE.2013 IEEE 27th International Symposium on Parallel and Distributed Processing.IEEE, Cambridge, MA, USA, 2013: 1133-1144.
|
| [8] |
JI Y, SUN J, NICA A, et al.Quality-driven disorder handling for m-way sliding window stream joins[C]//IEEE.32nd IEEE International Conference on Data Engineering.IEEE, Helsinki, Finland, 2016: 493-504.
|
| [9] |
JI Y, ZHOU H, JERZAK Z, et al.Quality-driven processing of sliding window aggregates over out-of-order data streams[C]//ACM.Proceedings of the 9th ACM International Conference on Distributed Event-Based Systems.ACM, Oslo, Norway, 2015: 68-79.
|
| [10] |
JI Y, ZHOU H, JERZAK Z, et al.Quality-driven continuous query execution over out-of-order data streams[C]//The 2015 ACM SIGMOD International Conference on Management of Data.ACM, Melbourne, Victoria, Australia, 2015: 889-894.
|
| [11] |
杨宁, 许嘉, 吕品, 等. 基于混合处理模型的乱序数据流分布式聚合查询处理技术[J]. 广西科学, 2019, 26(4): 398-404. DOI:10.3969/j.issn.1005-9164.2019.04.007 |
| [12] |
KRÄMER J, SEEGER B. Semantics and implementation of continuous sliding window queries over data streams[J]. ACM Transactions on Database System, 2009, 34(1): 1-49. |
| [13] |
LIU M, LI M, GOLOVNYA D, et al.Sequence pattern query processing over out-of-order event streams[C]//The 25th International Conference on Data Engineering.IEEE, Shanghai, China, 2009: 784-795.
|
| [14] |
周春姐, 戴鹏飞, 李洪波, 等. 物联网中具有时间持续性特征的乱序事件查询处理技术研究[J]. 计算机科学, 2016, 43(5): 179-187. |
| [15] |
MENCAGLI G, TORQUATI M, DANELUTTO M, et al. Parallel continuous preference queries over out-of-order and bursty data streams[J]. IEEE Transactions on Parallel & Distributed Systems, 2017, 28(9): 2608-2624. |
| [16] |
MUTSCHLER C, PHILIPPSEN M.Reliable specula-tive processing of out-of-order event streams in generic publish/subscribe middlewares[C]//The 7th ACM International Conference on Distributed Event-Based Systems.ACM, Arlington, Texas, US, 2013: 147-158.
|
| [17] |
MUTSCHLER C, PHILIPPSEN M. Adaptive speculative processing of out-of-order event streams[J]. ACM Transactions on Internet Technology, 2014, 14(1): 1-24. |
| [18] |
AGHABOZORGI S R, SHIRKHORSHIDI A S, TEH Y W. Time-series clustering-A decade review[J]. Information System, 2015, 53: 16-38. DOI:10.1016/j.is.2015.04.007 |
| [19] |
MUKHOTI J, RAKSHIT P, BHATTACHARYA D, et al.Knowledge extraction from a time-series using segmentation, fuzzy matching and predictor graphs[C]//2016 IEEE International Conference on Fuzzy Systems.IEEE, Vancouver, BC, Canada, 2016: 1201-1208.
|
| [20] |
JACQUES-SILVA G, LEI R, CHENG L W, et al. Providing streaming joins as a service at Facebook[J]. Proceeding of the VLDB Endowment, 2018, 11(12): 1809-1821. DOI:10.14778/3229863.3229869 |
| [21] |
朱睿, 王斌, 杨晓春, 等. 基于高速乱序流的Top-k连续查询算法[J]. 计算机学报, 2018, 41(8): 1693-1708. |
| [22] |
许嘉, 宋超, 吕品, 等. 基于EMD距离的数据流分布式相似性连接技术[J]. 计算机学报, 2019, 42(8): 1779-1796. |
| [23] |
GULISANO V, PAPADOPOULOS A V, NIKOLA-KOPOULOS Y, et al.Performance modeling of stream joins[C]//The 11th ACM International Conference on Distributed and Event-based Systems.ACM, Barcelona, Spain, 2017: 191-202.
|
| [24] |
LIN Q, OOI B C, W ZK W, et al.Scalable distributed stream join processing[C]//The 2015 ACM SIGMOD International Conference on Management of Data.ACM, Melbourne, Victoria, Australia, 2015: 811-825.
|
| [25] |
VISHWANATH R H, LEENA S, SRIKANTAIAH K C, et al. Forecasting stock time-series using data approximation and pattern sequence similarity[J]. International Journal of Information Processing, 2013, 7(2): 90-100. |



