2. 广西大学计算机与电子信息学院, 广西南宁 530004
2. College of Computer and Electronics Information, Guangxi University, Nanning, Guangxi, 530004, China
车载自组织网(Vehicular Ad Hoc Networks,VANETs)是指由路边单元、车辆之间构成的一种移动自组织网络,旨在提高交通安全系数,是智能交通的重要组成成分[1]。VANETs具有车辆高速移动的动态变化特点,容易造成其通信链路断裂而通信质量不佳。可靠而稳定的成簇算法可以实时传输数据,减少网络通信延迟,为智能交通系统奠定技术基础。
为提高VANETs通信的可靠性以及稳定性,如何将VANETs更为准确地划分成簇,使得计算成本最小化和网络寿命周期最大化之间平衡,一些研究者将成簇算法用于VANETs中[2]。Gerla等[3]针对VANETs成簇的稳定性,提出一种基于节点的空间位置的最小ID成簇算法,给所有的节点标识唯一ID,将最小ID标识设置为簇头。该算法实现简单,计算成本低,但是牺牲了节点的负载均衡,不适用于高速移动的场景。Basu等[4]基于节点移动的差异提出最小相对移动成簇算法,该算法通过比较一个节点与其他节点的移动差异的方差来选择簇头,有效地提高了成簇的稳定性,但是也不适用于高速移动的场景。Chatterjee等[5]基于节点的移动特性、车辆流量以及节点能量提出一种按需加权的成簇算法,该算法较为全面地考虑了节点的特性,但是算法的计算成本也大大增加。许力文等[6]基于车辆的平均速度、位置和方向等信息,提出一种改进的K-means分簇算法,该算法利用改进的K-means算法划分成簇,再利用改进的Floyd-Warshall算法选择簇投,从而提高VANETs通信链路的稳定性。李炳圻等[7]考虑车辆的速度、位置和方向以及节点间的QoS提出了一种SQ-WCA成簇算法,实验表明该算法在VANETs中具有稳定性和可靠性。
K-means算法[8]是基于划分的常见聚类算法之一,具有实现简单、较强的局部搜索能力、时间复杂度接近线性等优点,但是也存在一些不足,如对初始聚类中心依赖、容易出现“早熟”现象等。所以,有学者将群智能优化算法与K-means算法结合一起,例如粒子群优化算法[9-10]、人工蜂算法(Artificial Bee Colony, ABC)[11]等。作为一种新颖的群智能优化算法,人工蜂算法是于2005年通过模拟蜂群的采摘蜂蜜过程而被提出,目前已经成功应用于入侵检测[12]、图像分割[13]、组合优化问题[14]等多个领域。这里提出一种基于改进人工蜂的K-means优化聚类算法,并将其应用到VANETs分簇中。通过改进人工蜂算法中蜂群的迭代搜索获取全局最优的K个聚类中心,在此基础上执行K-means算法划分聚类,充分利用人工蜂算法的勘探能力和K-means算法的开发能力,避免过早陷入局部最优,消除K-means算法对初始聚类中心选取的依赖性,获取近似全局最优的聚类划分,提高算法的收敛速度以及改善聚类结果的质量。
1 材料与方法 1.1 人工蜂算法人工蜂算法是Karaboga等[15]提出的一种新颖的全局优化算法,其灵感来源于蜂群的采蜜过程,蜜蜂各司其职,具有独特的正反馈机制,蜂群之间能够实现信息交互,进而快速寻找到最优解。标准的人工蜂算法[16]包括蜜源、采蜜蜂(跟随蜂)、引领蜂和侦察蜂,算法的目的是尽可能找到量多的蜜源。基本的人工蜂群算法具体步骤如下:
Step 1:初始化算法基本参数,算法的最大迭代次数MaxIter,蜜源的最大迭代次数Limit,以式(1)方式产生SN个初始蜜源(采蜂蜜)xid;
| $ {{x}_{id}}=x_{_{d}}^{^{\text{min}}}+\text{rand}\left( 0, 1 \right)(x_{d}^{\max }-x_{d}^{\min }), $ | (1) |
其中,i是蜜源的数量,i∈(1, 2, …, SN),d是蜜源的维度,xdmax、xdmin分别是解的上、下边界;
Step 2:计算各个蜜源的适应度值fit,记录各个蜜源的最好适应度值fit_pbest、所有蜜源中最好适应度值fit_gbest以及对应的蜜源;
Step 3:引领蜂通过式(2)的方式产生新蜜源x'id。若新蜜源的fit大于fit_pbest则引领蜂保留新蜜源,否则不更新;
| $ ~x{{'}_{id}}={{x}_{id}}+r\left( -1, 1 \right)\left( {{x}_{id}}-{{x}_{kd}} \right), $ | (2) |
其中,xkd表示相邻蜜源,k∈(1, 2, …, SN),且k≠i;
Step 4:算法根据公式(3)计算每个蜜源的适应度值在所有蜜源的适应度值之和中所占的比重pi:
| $ ~{{p}_{i}}=\frac{\text{fi}{{\text{t}}_{i}}}{\sum\limits_{j=1}^{\text{SN}}{\text{fi}{{\text{t}}_{j}}}}, $ | (3) |
其中,fiti表示第i个蜜源对应的适应度值;
Step 5:跟随蜂通过轮盘赌的选择方式选择蜜源,利用公式(2)进行更新操作,若新蜜源的fit大于fit_pbest则跟随蜂保留新蜜源,否则不更新;
Step 6:侦察蜂的转换机制,假设某个蜜源经过limit次迭代后适应度值仍然保持不变,说明可能陷入局部最优解,与此蜜源对应的引领蜂将放弃此蜜源并转变为侦察蜂,然后用式(1)随机生成新蜜源,侦察蜂开始对这个新蜜源进行搜索并再次转变为引领蜂;
Step 7:记录最优蜜源gbest;
Step 8:判断是否达到算法最大迭代次数,如否,则转到Step 3,如是,则运行结束。
1.2 K-means算法K-means算法是根据相似性原则计算平方误差函数来作为评判标准,将一组数据X={x1, x2, …, xn}划分到K个类簇C={c1, c2,…,ck}中,满足簇间数据相似最小化,簇内数据相似最大化的要求。
算法的运行过程如下[10]:
Step 1:给定类数K并随机选取K个对象作为初始聚类中心;
Step 2:分别计算每个数据对象xi与所有类中心的距离d(xi, cj),并根据最近邻原则将其划分;
Step 3:重新计算类内所有数据对象的均值作为各个新形成聚类的聚类中心;
Step 4:重复执行Step 2-Step 3,直到聚类中心不发生变化,则算法结束。
1.3 人工蜂与K-means混合算法在VANETs分簇中的应用人工蜂与K-means混合算法解决VANETs的分簇问题需要解决蜜源编码以及适应度函数设计两个问题。
1.3.1 蜜源编码方式根据数据集xi,划分簇数K和特征数m,搜索空间解可表示为K*m的向量:即(c11, c12, c1m, …, cK1, cK2, cKm)。
1.3.2 适应度函数设计一般而言,将平方误差I作为评价聚类质量的标准,但是在ABC中的目的是搜索花蜜量最大的蜜源,聚类算法中I越小说明聚类效果越好,人工蜂与K-means混合算法适应度函数设计如公式(4)(5)所示,蜜源位置对应聚类中心位置:
| $ I=\sum\limits_{j=1}^{K}{\sum\limits_{{{x}_{i}}\in {{c}_{j}}~}{\|{{x}_{i}}-{{c}_{j}}\|}}, $ | (4) |
| $ ~f\left( x \right)=1-{{(1+I)}_{\circ }} $ | (5) |
K-means算法是基于划分的常见聚类算法之一,人工蜂群算法是一种新颖的全局优化算法,综合两者,提出一种基于改进人工蜂的K-means优化聚类算法,通过改进人工蜂算法中蜂群的迭代搜索获取全局最优的K个聚类中心,在此基础上执行K-means算法划分聚类,充分利用人工蜂算法的勘探能力和K-means算法的开发能力,避免过早陷入局部最优,消除K-means算法对初始聚类中心选取的依赖性,加快收敛速度。将ABC的适应度函数fit设定为与K-means聚类的衡量准则函数相关的函数,经过不断地迭代返回适应度最优的蜜源,聚类中心点集就是使K-means聚类的类内距离和最小的解,然后以这组聚类中心进行K-means聚类得到最优的聚类效果。
1.3.4 人工蜂与K-means混合算法伪代码综上,人工蜂与K-means混合算法实现过程如下:
Step 1:从数据集X中随机选择K个中心点,将其作为蜜源xi初值;
Step 2:执行ABC算法进行迭代搜索(见人工蜂算法实现流程);
Step 3:执行K-means算法,按照类输出即最终的聚类结果(见K-means算法实现流程)。
1.3.5 簇的形成结合十字路口VANETs的场景,车辆在交通规则限定下以非匀速前进,利用人工蜂与K-means混合算法应用于其分簇,可以提高车辆之间的通信质量。簇的形成通过人工蜂算法进行,其主要思想是代替K-means获取车辆节点分类的聚类点。
1.3.6 簇头的选择在簇头选取阶段,仅仅把混合算法最终输出的车辆划分类的质心作为簇头,只是依据位置来选择而未考虑到速度,簇内计算所有VANETs车辆的最短距离,将具有到其余车辆的最小平均距离且具有最小速度方差的车辆选择为簇头。参照文献[6],利用位置以及速度方差进行簇头的选择,根据黄金比例,速度方差VAR给予w1(0.618)的权重,平均距离AD给予w2(0.382)的权重。具有最小的合计分值(Total Score, TS)的车辆节点将被选择为簇头的候选。其计算方式是
| $ \text{T}{{\text{S}}_{i}}=\text{count}{{({{w}_{1}}\text{VAR}\left( {{V}_{i}} \right)+{{w}_{2}}\text{AD}({{V}_{i}}))}_{\circ }} $ | (6) |
在簇的维护阶段,当最优节点的簇头有变化时,次优节点被入选临时簇头,直至最优节点代替次优节点再次更新簇头信息。
1.4 实验环境及参数设置实验环境是MATLAB 2015Ra,Inter(R) Xeon(R) CPU E5-1620 v3 @3.5 GHz,win8操作系统。人工蜂与K-means混合算法的各个参数取值如下:ABC算法蜜源个数SN=20,种群规模NP=40;算法的最大迭代次数MaxIter=500,蜜源的最大迭代次数Limit=20,算法运行30次。十字路口的场景设置为每个车辆可以在1 000 m内运动,速度为60-120 km/h,车辆节点数目是10-100,通过比较分析人工蜂与K-means混合算法、PSO与K-means混合算法[17]、K-means算法[6],主要从成簇的稳定性、端到端时延评价算法的性能。
2 结果与分析根据公式(6),TS越小,簇头的稳定性越好。表 1是其中一个簇内选择簇头的过程。
根据表 1可知,车辆ID 4具有最小的TS值,因此适合作为簇头。而仅仅以距离来衡量车辆的簇头稳定性是不全面的,如表 1中,车辆ID 6具有最小的平均距离(AD),但与其他车辆的速度差很大,如果选作簇头,较大的速度差将影响簇头的持续时间和平均距离。
| ID | 平均距离 AD (m) |
速度方差 VAR (m) |
TS |
| 1 | 11 | 68 | 46.23 |
| 2 | 14 | 51 | 36.87 |
| 3 | 43 | 64 | 55.98 |
| 4 | 16 | 43 | 32.69 |
| 5 | 44 | 87 | 70.57 |
| 6 | 9 | 94 | 61.53 |
| 7 | 96 | 19 | 48.41 |
| 8 | 57 | 27 | 38.46 |
| 9 | 63 | 56 | 58.67 |
| 10 | 44 | 69 | 59.45 |
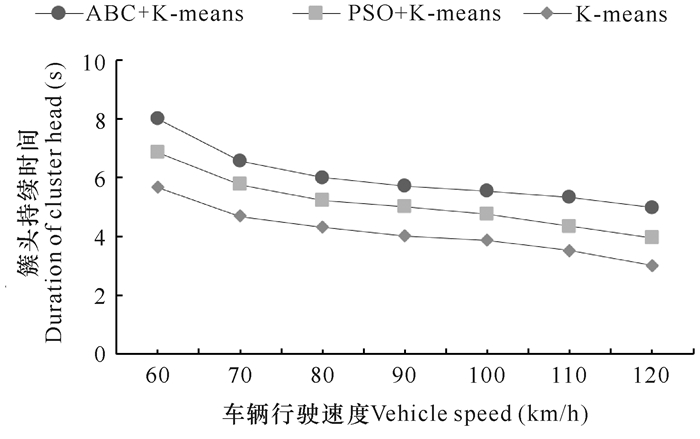
3种算法的簇头节点持续时间车辆速度变化如图 1所示。随着速度的增大,3种算法的簇头持续时间整体减少,这是因为速度增大,网络拓扑结构频繁变化。簇头持续时间减少,导致通信链路变差,算法的稳定性就越差。而在相同的速度下,人工蜂与K-means混合算法簇头持续时间是最长的,因为该算法不仅考虑了速度,还考虑了位置的因素,使得形成的簇比较稳定,通信链路也比较稳定。
|
| 图 1 簇头节点持续时间变化曲线图 Fig. 1 Curve of cluster head duration |
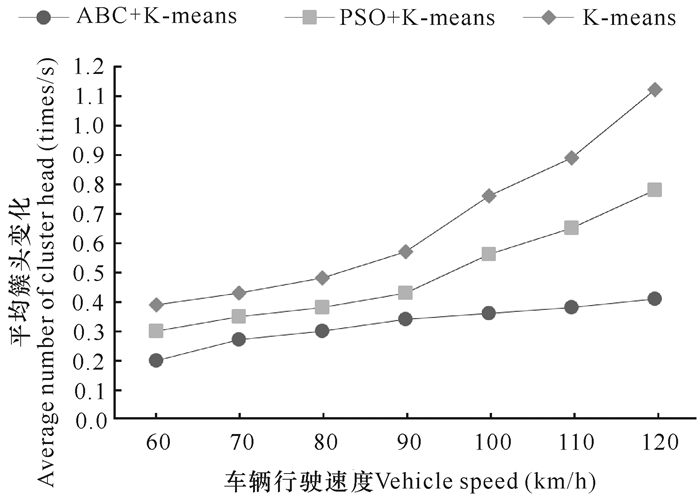
图 2显示3种算法在不同速度下平均簇头变化次数变化情况。随着速度的增大,3种算法的平均簇头平均变化次数逐渐增大,与簇头持续时间呈反比,说明簇头持续时间越长,通信质量越稳定,簇头平均变化次数越少。在相同速度下,人工蜂与K-means混合算法的平均簇头变化次数是最小的,说明该算法比其他2种算法稳定。
|
| 图 2 平均簇头变化次数曲线图 Fig. 2 Curve of average number of cluster head |
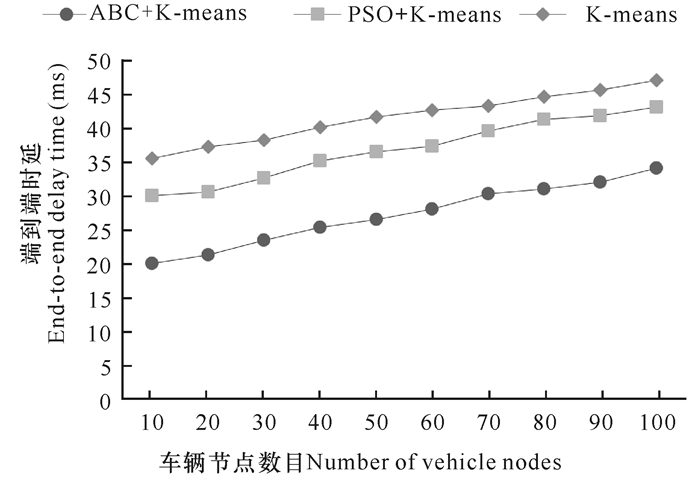
图 3是3种算法有关车辆节点与端到端时延的变化情况。随着车辆节点数目增大,会增加3种算法的端到端时延。车辆密度会影响车辆节点端到端时延。较稳定的簇头兼具有较好的信道质量,可以降低端到端时延,加快通信链路的传输。在相同的车辆节点数目下,人工蜂-K-means混合算法具有最低的端到端时延,说明该算法对通信质量的提升程度比其他2种算法更佳。
|
| 图 3 端到端时延变化曲线图 Fig. 3 Curve of end-to-end delay time |
综上,用人工蜂与K-means混合算法求解VANETs分簇问题是可行有效的,且比PSO与K-means混合算法、K-means算法性能更佳,主要原因有:(1)K-means算法过度依赖于初始聚类中心的选择,而人工蜂与K-means混合算法利用人工蜂算法作为寻找初始聚类中心的搜索策略,再利用K-means算法进行聚类输出最终结果,消除依赖性。(2)相比PSO和K-means混合算法,人工蜂与K-means混合算法具有更强大的全局搜索能力,使得该算法更快速寻找到最优解。(3)相对于其他2种算法,人工蜂与K-means混合算法充分考虑位置和速度影响因素,更加全面地说明该算法的可靠性。
3 结论VANETs的车辆节点具有动态的特性,网络拓扑结构频繁变化导致通信链路不稳定。这里将人工蜂与K-means混合算法用于VANETs分簇中,即把场景内的车辆节点通过人工蜂算法分成不同集群,在利用K-means算法进行聚类结果的输出。通过改进人工蜂算法中蜂群的迭代搜索获取全局最优的K个聚类中心,在此基础上执行K-means算法划分聚类,充分利用人工蜂算法的勘探能力和K-means算法的开发能力,避免过早陷入局部最优,消除K-means算法对初始聚类中心选取的依赖性,加快收敛速度。分簇的稳定性影响集群通信链路的通信质量,稳定的簇头可以更好地维持分簇的形状以及簇头持续时间。在以后的工作中,应对VANETs进行更深入的研究,尝试将其他智能算法与K-means结合,并应用于VANETs中。
| [1] |
马金忠, 王文杰, 田彦山. 城市车联网中紧急消息的快速广播路由研究[J]. 西南师范大学学报:自然科学版, 2019(6): 84-91. |
| [2] |
COOPER C, FRANKLIN D, ROS M, et al. A comparative survey of VANET clustering techniques[J]. IEEE Communications Surveys and Tutorials, 2017, 19(1): 657-681. |
| [3] |
GERLA M, TSAI J T C. Multicluster, mobile, multimedia radio network[J]. Wireless Networks, 1995, 1(3): 255-265. |
| [4] |
BASU P, KHAN N T D C.A mobility based metric for clustering in mobile ad hoc networks[C]//Proceedings 21st International Conference on Distributed Computing Systems Workshops, Mesa, AZ, USA: IEEE, 2001. https://www.researchgate.net/publication/3895235_A_Mobility_Based_Metric_for_Clustering_in_Mobile_Ad_Hoc_Networks
|
| [5] |
CHATTERJEE M, DAS S K, TURGUT D. WCA:A weighted clustering algorithm for mobile ad hoc networks[J]. Cluster Computing, 2002, 5(2): 193-204. |
| [6] |
许力文, 乔丽娟, 陈杰. 基于VANETs修改的K-means分簇路由算法[J]. 计算机技术与发展, 2018, 28(3): 15-19. |
| [7] |
李炳圻, 梅中辉. 一种适用于城市环境的VANET成簇算法[J]. 计算机技术与发展, 2019, 29(1): 154-158. |
| [8] |
余秀雅, 刘东平, 杨军. 基于K-means++的无线传感网分簇算法研究[J]. 计算机应用研究, 2017, 34(1): 181-185. |
| [9] |
谢秀华, 李陶深. 一种基于改进PSO的K-means优化聚类算法[J]. 计算机技术与发展, 2014, 24(2): 34-38. |
| [10] |
徐艳.K-means算法与群体智能算法(PSO)融合的研究与应用[D].呼和浩特市: 内蒙古农业大学, 2019. http://cdmd.cnki.com.cn/Article/CDMD-10129-1019212918.htm
|
| [11] |
于佐军, 秦欢. 基于改进蜂群算法的K-means算法[J]. 控制与决策, 2018, 33(1): 181-185. |
| [12] |
刘铭, 黄凡玲, 傅彦铭, 等. 改进的人工蜂群优化支持向量机算法在入侵检测中的应用[J]. 计算机应用与软件, 2017, 34(1): 230-235. |
| [13] |
赵文昌, 李忠木. 融合改进人工蜂群和K均值聚类的图像分割[J]. 液晶与显示, 2017, 32(9): 726-735. |
| [14] |
张懿. 人工蜂群算法在投资组合问题中的优化应用[J]. 计算机与数字工程, 2019, 47(8): 1869-1873, 1894. |
| [15] |
KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8(1): 687-697. |
| [16] |
ZHANG X, ZHANG X, GU C. A micro-artificial bee colony based multicast routing in vehicular ad hoc networks[J]. Ad Hoc Networks, 2017, 58(2): 213-221. |
| [17] |
汤深伟, 贾瑞玉. 基于改进粒子群算法的k均值聚类算法[J]. 计算机工程与应用, 2019, 55(18): 140-145. |



