2. 南昌大学信息工程学院电子信息工程系, 江西南昌 330031
2. Department of Electronic Information Engineering, Information Engineering School of Nanchang University, Nanchang, Jiangxi, 330031, China
混沌系统因为对初始条件以及系统参数具有高敏感性、伪随机性和非线性等重要特征而被普遍应用于各种保密通信系统。基于混沌系统的各种图像加密算法不断地被提出[1-3]。相对于低维的混沌系统而言,高维的混沌系统复杂程度更高,且存在李雅普诺夫指数,具有更复杂的动态行为和高随机性,能够很好地增加图像加密系统的安全性能[4-13]。Ye[4]通过将Toeplitz矩阵和Hankel矩阵相结合的方法,实现对图像的加密,并且利用Chen氏混沌系统理论对图像的灰度值进行扩散,以加强系统的保密性。Gao等[5]利用超混沌系统混淆明文与密文之间的联系,从而实现图像加密。随后,将该系统基本的动力学特征经过Lyapunov指数和特征方程改进,使得系统中的参数可调[6]。Gao等[7]又将超混沌系统与神经细胞网络相结合用于图像认证,将图像像素值用HCCNN传输,从而产生秘密信息用于身份验证。Zhu等[8]设想了结合中国剩余定律的超混沌系统加密方法,先通过超混沌系统对图像的像素进行置乱,再用中国剩余定律对置乱的结果实行扩散、压缩,实现图像的加密。Hermassi等[9]对超混沌图像加密系统进行加强,显著地提高系统的加密速度。Zhu[10]对超混沌序列的图像加密方案做了改进,此算法将超混沌序列和明文信息的正确密钥同时加密,增加密钥的复杂度。秦怡等[11]在一种改进的光学联合变换相关加密系统中,利用附加密钥旋转实现多幅二值图像的加密。Pan等[12]联合非线性分数梅林变换和离散余弦变换,提出光学多图像加密方案,Zhou等[13]在此基础上基于共稀疏表示和随机像素交换,提出双图像压缩加密算法。本文联合超混沌系统和离散分数随机变换,提出一种图像加密新方案,与单纯的离散分数随机变换的图像加密算法相比,在不增加计算负担的情况下,本算法的明文与密文之间具有更高的复杂性,并加大了密钥空间,提高了密钥敏感性, 同时给出了实现该算法的光学装置原理图。
1 理论基础 1.1 超混沌系统Chen氏超混沌系统的定义如下:
| $ \left\{ \begin{align} & \dot{x}=a\left( y-x \right)\text{ } \\ & \dot{y}=dx-xz+cy-h \\ & \dot{z}=xy-bz \\ & \dot{h}=x+k~ \\ \end{align} \right., $ | (1) |
其中a, b, c, d和k是超混沌系统的参数。当参数a=36, b=3, c=28, d=-16, -0.7<k < 0.7时,该系统处于超混沌状态,能产生4个混沌序列。假设k=0.2,那么其李雅普诺夫指数分别为λ1=1.552, λ2=0.023, λ3=0和λ4=-12.573。
1.2 离散分数随机变换一维信号x的离散随机变换表示为
| $ \Re {{~}^{\alpha }}\left( x \right)={{R}^{\alpha }}x, $ | (2) |
其中,
| $ {{R}^{\alpha }}=M{{F}^{\alpha }}{{M}^{t}}, $ | (3) |
其中M是本征向量矩阵,MMt=I。Fα是随机变换本征值的对角矩阵,即
| $ \begin{align} & \ \ \ \ \ {{F}^{\alpha }}=\text{diag}~\left\{ 1, \text{exp}\left( -\frac{i2\pi \alpha }{T} \right), \text{exp}\left( -\frac{i4\pi \alpha }{T} \right), \cdot \cdot \cdot , \right. \\ & \left. \text{exp}\left[ -\frac{i2\left( N-1 \right)\pi \alpha }{T} \right] \right\}, \\ \end{align} $ | (4) |
其中T是离散分数随机变换的周期。核矩阵Rα是随机变换的核心,它由一个对称随机矩阵W来控制,矩阵W由N×N的随机矩阵B生成。
| $ W=\frac{B+{{B}^{t}}}{2}, $ | (5) |
因为B是随机的,所以Rα具有随机性,不同的矩阵B对应不同的变换结果。
2 图像加密算法 2.1 加密过程本文根据Chen氏理论,利用超混沌系统生出的混沌序列,来控制随机变换中的随机矩阵B,从而实现图像加密。该算法的详细加密过程描述如下:
步骤1:选择混沌系统的初始条件x0, y0, z0, h0, 使用Runge-Kutta方法迭代Chen氏超混沌系统n0=22n次,得到4个超混沌序列{ti|i=1, 2, …, 2n },t分别为x, y, z和h。
步骤2:将序列{ti|i=1, 2, …, n }中的每个元素进行取整运算,获得整数序列ti*。
| $ ~{{t}^{*}}_{i}=\left| \left\lfloor \left( {{t}_{i}}-\left\lfloor {{t}_{i}} \right\rfloor \right)\times {{10}^{14}} \right\rfloor \right|\text{mod}256, $ | (6) |
其中
步骤3:步骤2中的4个整数序列被用来构建一个超混沌新序列K={k1, k2, …, k2n}。如果hi*mod3=0,则ki=xi*作为随机矩阵B的第i个元素;同样地,若hi*mod3=1或hi*mod3=2时,则分别取ki=yi*或ki=zi*作为随机矩阵B的第i个元素;整数序列ki可以用8位二进制表示,即ki>=pi7pi6pi5…pi0,其中pij∈ 0, 1, i=1, 2, …, 22n, j=0, 1, …, 7。
步骤4:将步骤3中的混沌序列构建的随机矩阵B代入上式(5),得到对称随机矩阵W。用数值计算的方法求出W正交化和归一化后的本征矩阵M。结合式(2)、(3)和(4)获得随机变换的结果,即加密图像。
本算法的密钥包括Chen氏超混沌系统的4个初始值(x0, y0, z0, h0)以及离散分数随机变换的阶次α。解密过程使用的密钥与加密时使用的密钥完全一致。
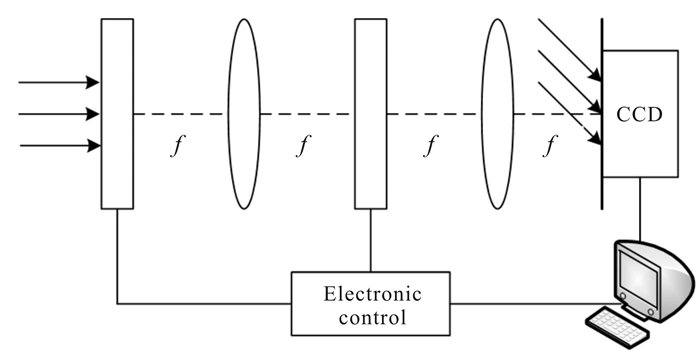
2.2 光学实现原理离散分数随机变换可以利用傅里叶变换域中的随机相位滤波在一个典型的4f系统中进行光学实现[14],相应的加密光学装置如图 1所示。在输入平面以及傅里叶频谱面上分别摆放互相不关联的随机相位模板,通过相位模板完成对输入的图像加密,在输出的平面上即可获得加密的图像。相应的随机反变换可以通过随机相位复共轭过滤器与傅里叶反变换实现。
|
| 图 1 加密方案光学实现原理图 Fig. 1 Optical implementation devices of the proposed image encryption scheme |
3 实验仿真
本方案选取尺寸为256×256像素的灰度图像“Lena”“Man”和“Lake”作为测试图像,如图 2所示。在加密过程中,Runge-Kutta方法所用步长定为0.001,Chen氏系统4个初始值x0, y0, z0, h0分别设为0.3, 0.4, 0.5, 0.6,离散分数随机变换的阶次α为0.2。加密图像如图 2d、e和f所示,解密图像如图 2g、h和i所示。实验解密得到的“Lena”“Man”和“Lake”图像与原图像间的MSE值分别为3.336 7×10-26,2.501 4×10-26和3.228 4×10-26。仿真结果显示MSE值非常小,表明该算法的解密图像的质量较高。

|
| 图 2 图片测试结果 Fig. 2 Results of images test |
3.1 相邻像素间的相关性
相关性系数的定义为
| $ ~C=\frac{\sum\limits_{i=1}^{N}{\left( {{x}_{i}}-\bar{x} \right)\left( {{y}_{i}}-\bar{y} \right)}}{\sqrt{\sum\limits_{i=1}^{N}{{{\left( {{x}_{i}}-\bar{x} \right)}^{2}}\sum\limits_{i=1}^{N}{{{\left( {{y}_{i}}-\bar{y} \right)}^{2}}}}}}, $ | (7) |
其中
图 3为测试图像“Lake”及其密文图像相邻像素间的相关性分布图,测试图像“Lena”和“Man”也具有相类似的结果。表 1列出测试图像“Lena”“Man”和“Lake”及其加密图像在水平、竖直、对角3个方向上的相关系数。表 1中的结果表明:原图像在不同方位上相邻像素之间均具有较大的相关性,加密图像在水平、竖直和对角方向上的相邻像素间的相关性显著降低,因此很难由少量的图像信息恢复出原明文的信息。

|
| 图 3 水平方向相邻像素间的相关性 Fig. 3 Correlation distribution of horizontally adjacent pixels |
| Correlation | Horizontal | Vertical | Diagonal |
| "Lena" | 0.957 9 | 0.927 8 | 0.897 4 |
| Encrypted "Lena" | 0.226 5 | 0.100 2 | 0.013 3 |
| "Man" | 0.929 1 | 0.911 4 | 0.888 2 |
| Encrypted "Man" | 0.195 0 | 0.047 2 | -0.005 8 |
| "Lake" | 0.935 8 | 0.941 9 | 0.902 0 |
| Encrypted "Lake" | 0.360 3 | 0.156 0 | -0.010 1 |
3.2 密钥敏感性分析
一般可以用均方误差函数(Mean Square Error,MSE)来权衡解密图像的质量,其定义如下:
| $ \text{MSE}=\frac{1}{L\times H}{{\sum\limits_{x, y}{\left[ I\left( x, y \right)-D\left( x, y \right) \right]}}^{2}}, $ | (8) |
其中,L×H表示图像总像素数,I(x, y)和D(x, y)分别为原文和密文在坐标(x, y)处的像素值。MSE值低,说明解密图像的质量好;MSE值高,表明原图像和解密图像之间的差别大,解密图像的质量差。
图 4是当密钥有微小改变时的解密“Lena”图,其中图 4a是其他密钥都正确的情况下使用α=0.195得到的解密图;图 4b-e为其他密钥均正确时,只使用有偏差的超混沌初始值x0=0.3+10-15,y0=0.4-10-15,z0=0.5+10-15,h0=0.6-10-15的解密后的图像。结果表明:虽然密钥偏差非常小,但是仍然无法解密得到任何关于原始图像的信息。

|
| 图 4 错误密钥解出的“Lena”图 Fig. 4 Decryption "Lena" with error key |
图像加密性能的另一个评价因素是密钥空间的大小。在该算法中,随机变换的分数阶次α和系统的4个初始值x0, y0, z0和h0被当作主要密钥。计算密钥空间大小的表达式为
| $ S=\prod\limits_{\text{ }j=1}^{4}{{{S}_{j}}}, $ | (9) |
其中Sj是第j个子密钥空间。
仿真结果表明,当分数阶次α偏差0.005作为密钥时无法得到原始图像的信息,因此分数阶次α的密钥空间大小约为200。图 4显示:当系统初始值与正确的密钥相差10-15时,也不能得到原始图像的信息,所以每个初始值的密钥空间大小约为10-15。因此,该算法的总密钥空间为
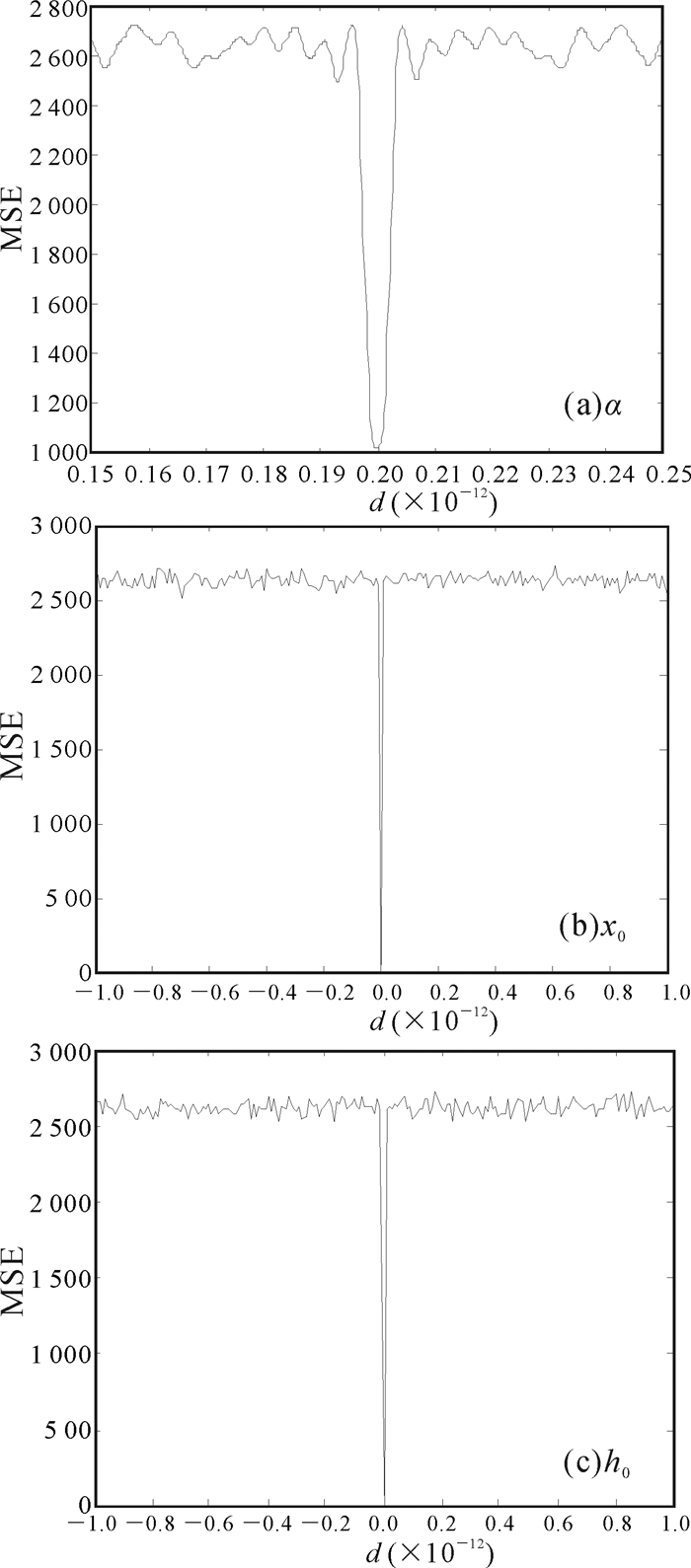
图 5a是随机变换的分数阶次α的均方误差曲线,正确的分数阶次是0.2。曲线的变化趋势体现了解密图像的质量随分数阶次变化而变化的情况,当α的数值发生一定程度的偏差,均方误差就会急剧上升。图 5b和c分别是混沌系统初始值x0和h0的均方误差曲线(y0和z0结果类似),显然,当初始值发生微小改变时,曲线的变化很明显。由图 4可知,混沌系统初始值偏离正确密钥10-15时已无法获取明文信息,说明该算法的密钥敏感性非常高,具有较强的安全性。由此可以总结出该加密算法具有很强的抵抗暴力攻击的能力。
|
| 图 5 MSE曲线 Fig. 5 MSE curves |
3.3 抗噪声分析
假设加密图像C受到噪声污染后为C′,即
| $ {{C}^{\prime }}=C+kG, $ | (10) |
其中k为噪声强度系数,G为零均值、单位标准差的高斯白噪声。
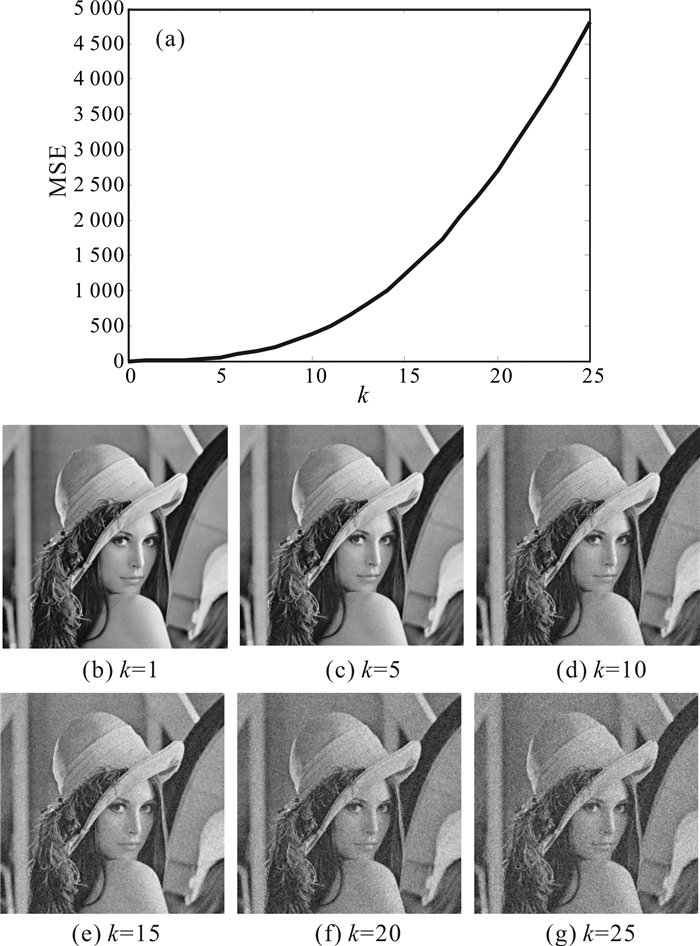
图 6a是在不同强度噪声污染下的解密图像的均方误差变化曲线。图 6b-g分别是对应噪声强度系数为1,5,10,15,20和25的解密图像。结果表明,随着噪声强度系数增大,解密图像的质量相应地降低,但是当k=25时, 依然可以清晰地辨别出原始图像的主要信息。经过加密的图像信息,在噪声污染程度不高的情况下,仍能获得质量较好的解密图像,因此该算法具有一定的鲁棒性。
|
| 图 6 噪声攻击结果 Fig. 6 Results of noise attacks |
3.4 抗剪裁性分析
由于外界传输故障等原因,图像在传输过程中可能部分密文信息被丢失。图 7a横裁图像中间部分,图 7b竖裁图像中间部分,图 7c随机对图像剪裁一个三角形,图 7d剪裁图像的4个角,图 7e-h分别是对应的解密图像。解密后的图像比较模糊,但是仍然可以辨别出原始图像的大致信息,说明本加密算法具有一定的抗剪裁攻击能力。

|
| 图 7 抗剪裁性测试结果 Fig. 7 Test result of tailoring resistance |
4 结论
本文结合超混沌系统和离散分数随机变换,提出了一种图像加密新方案,并给出了实现该算法的光学装置原理图。研究结果表明
(1) 与单纯的离散分数随机变换的图像加密算法相比,在不增加计算负担的前提下,本算法明文与密文之间具有更高的复杂性,并加大了密钥空间。
(2) 该系统是一个非线性的密码系统,消除了传统加密系统中因为线性过程而存在的不安全因素,提高了加密系统的抗攻击能力。
(3) 本文分别从相邻像素间的相关性、密钥的敏感性、噪声攻击以及裁剪攻击等4个方面对该算法进行实验分析,结果表明该算法具有较高的安全性,能够有效抵抗统计攻击、噪声攻击以及剪裁攻击。
| [1] |
HUANG F, FENG Y. An image encryption approach based on a chaotic map by diagonal stretch[J]. Journal of Optoelectronics Laser, 2008, 19(1): 100-103, 110. |
| [2] |
WANG X Y, GU S X, ZHANG Y Q. Novel image encryption algorithm based on cycle shift and chaotic system[J]. Optics and Lasers in Engineering, 2015, 68: 126-134. DOI:10.1016/j.optlaseng.2014.12.025 |
| [3] |
CHEN J X, ZHU Z L, FU C, et al. Optical image encryption scheme using 3-D chaotic map based joint image scrambling and random encoding in gyrator domains[J]. Optics Communications, 2015, 341: 263-270. DOI:10.1016/j.optcom.2014.12.045 |
| [4] |
YE G D. A chaotic image cryptosystem based on Toeplitz and Hankel matrices[J]. The Imaging Science Journal, 2009, 57(5): 266-273. DOI:10.1179/136821909X12490307952919 |
| [5] |
GAO T G, CHEN Z Q. A new image encryption algorithm based on hyper-chaos[J]. Physics Letters A, 2008, 372(4): 394-400. DOI:10.1016/j.physleta.2007.07.040 |
| [6] |
GAO T G, GU Q L. Analysis of transition between chaos and hyper-chaos of an improved hyper-chaotic system[J]. Chinese Physics B, 2009, 18(1): 84-90. |
| [7] |
GAO T G, GU Q L, EMMANUEL S. A novel image authentication scheme based on hyper-chaotic cell neural network[J]. Chaos Solitons & Fractals, 2009, 42(1): 548-553. |
| [8] |
ZHU H G, ZHAO C, ZHANG X D. A novel image encryption-compression scheme using hyper-chaos and Chinese remainder theorem[J]. Signal Processing:Image Communication, 2013, 28(6): 670-680. DOI:10.1016/j.image.2013.02.004 |
| [9] |
HERMASSI H, RHOUMA R, BELGHITH S. Im-provement of an image encryption based on hyper-chaos[J]. Telecommunication Systems, 2013, 52(2): 539-549. |
| [10] |
ZHU C X. A novel image encryption scheme based on improved hyperchaotic sequences[J]. Optics Communications, 2012, 285(1): 29-37. |
| [11] |
秦怡, 吕晓东, 巩琼, 等. 利用附加密钥旋转在光学联合相关结构中实现二值图像加密[J]. 光学学报, 2013, 33(3): 96-102. |
| [12] |
PAN S M, WEN R H, ZHOU Z H, et al. Optical multi-image encryption scheme based on discrete cosine transform and nonlinear fractional Mellin transform[J]. Multimedia Tools and Applications, 2017, 76(2): 2933-2953. DOI:10.1007/s11042-015-3209-x |
| [13] |
ZHOU N R, JIANG H, GONG L H, et al. Double-image compression and encryption algorithm based on co-sparse representation and random pixel exchanging[J]. Optics and Lasers in Engineering, 2018, 110: 72-79. DOI:10.1016/j.optlaseng.2018.05.014 |
| [14] |
LANG J, TAO R, WANG Y. Image encryption based on the multiple-parameter discrete fractional Fourier transform and chaos function[J]. Optics Communications, 2010, 283(10): 2092-2096. DOI:10.1016/j.optcom.2010.01.060 |


