2. 广西壮族自治区环境保护科学研究院, 广西南宁 530022
2. Guangxi Research Institute of Environmental Protection, Nanning, Guangxi, 530022, China
城市中近地面的臭氧是由人类活动排放的NOx、CO和VOCs等前体物在特定大气环境条件下发生复杂的化学反应生成的二次污染物[1]。近年来随着城市机动车保有量的激增,南宁近地面空气中O3污染问题日益严重,已成为南宁市大气污染防治重点工作之一。如何准确预报近地面臭氧浓度成为当前一个热门研究课题。
目前大气污染物浓度预测主要分为数值预测[2-3]和统计预测[4-8]两种方法。由于气象条件的复杂性,以大气动力学理论为基础的数值模式污染物浓度预测方法需要消耗大量的计算时间。而基于统计模型的预测方法通常采用真实监测值,利用统计方法,建立预测模型,具有计算速度快的特点。时间序列模型作为统计预测法之一,已被广泛用于大气污染物浓度预测[9],但主要还是集中在PM10、NOx等污染物的预测[10-13]上,用于O3浓度预测仍比较少。
本文通过构建ARMA-GARCH模型,对南宁市城区O3浓度进行预测,并对预测模型进行误差评价,期望为大气污染防治和预警预报提供支持。
1 材料与方法 1.1 数据来源本研究以南宁市2017年1月1日-2017年12月31日日均O3浓度监测值为样本,数据来源于广西壮族自治区环境保护厅、广西壮族自治区环境监测中心站按照《环境空气质量指数(AQI)技术规定(试行)》的有关要求,实时发布的南宁市市区环境空气自动监测站点,数据真实可靠。本研究使用EViews软件对样本拟合模型,预测2018年1月1日至2018年1月31日O3日均浓度,并对预测结果进行误差分析和模型评价。
1.2 ARMA-GARCH建模基本原理 1.2.1 ARMA模型时间序列是变量按时间间隔的顺序形成的随机变量序列,时间序列分析通常不需要建立在专业理论所体现的相互关系基础之上,而是“让数据自己说话”。本研究选用移动平均自回归模型即ARMA模型。ARMA模型是描述平稳时间序列最常用的分析模型,由统计学家Box G.E.P.和Jenkins G.M.于20世纪70年代创立,用此模型对时间序列进行预测分析称为博克斯-詹金斯(B-J)方法。其基本思想是构成时序的单个序列值虽然具有不确定性,但整个序列的变化具有一定的规律性,可以运用时间序列的过去值、当期值及滞后扰动项的加权和建立模型来“解释”时间序列的变化规律[14]。
ARMA(p,q)模型的一般形式为
| $ \begin{array}{l} \;\;\;\;\;\;\;{x_t} = {\rm{C}} + {\alpha _1}{x_{t - 1}} + \cdot \cdot \cdot + {\alpha _p}{x_{t - p}}\;\;\;\;{\theta _1}{\mu _{t - 1}}\;\;\; \cdot \cdot \cdot \\ {\theta _q}{\mu _{t - q}} + {\mu _t}, \end{array} $ |
其中参数C为常数,α是自回归模型系数,θ是移动平均模型系数,μt是满足独立同分布的随机误差项(扰动项)。当C=0,该模型成为中心化ARMA(p,q)模型;当q=0时,上式变为p阶自回归模型,记为AR(p);当p=0时,上式称为q阶移动平均模型,记为MA(q)。
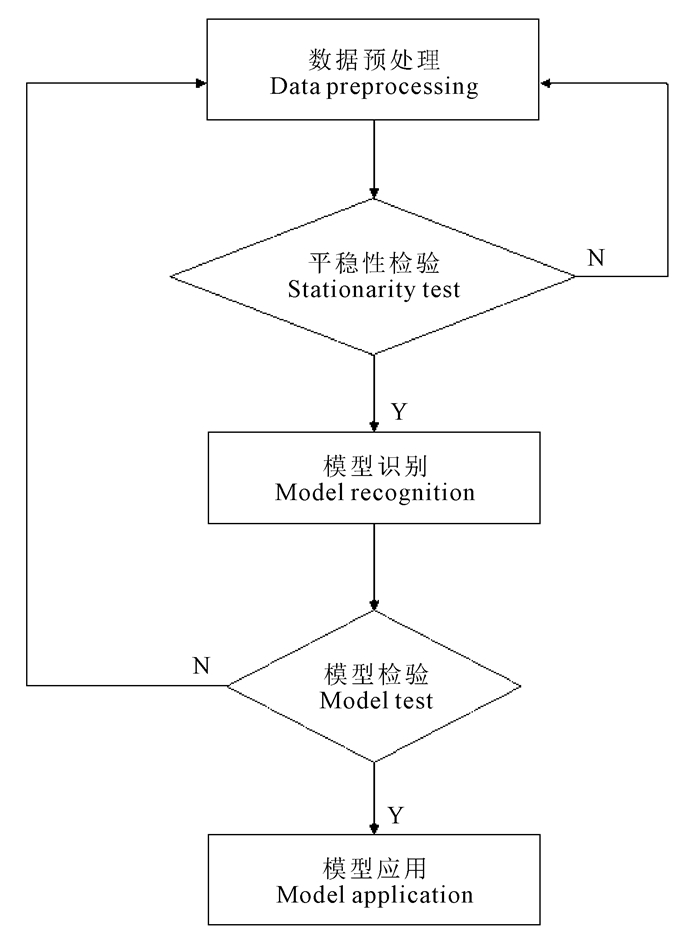
ARMA模型建立过程如图 1所示,主要由以下5个部分构成:
|
| 图 1 ARMA模型建模流程图 Fig. 1 Modeling flowchart of ARMA model |
(1) 数据预处理。通过时序图初步判断数据是否具有周期性、趋势性、随机性等特点。若存在相应特点,则对原始数据进行差分、对数变换等处理。
(2) 平稳性检验。时间序列可以分为平稳序列和非平稳序列两大类。时间序列数据的平稳有以下要求:均值、方差不随时间变化;自相关系数只与时间间隔有关,而与所处时间无关。如果用传统方法对彼此不相关联的非平稳变量进行回归,t检验值和F检验值往往倾向于显著,从而得出“变量相依”的“伪回归结果”,因此,在利用回归分析方法讨论变量有意义的关系之前,必须对变量时间序列的平稳性与非平稳性进行判断[15]。
(3) 模型识别。通过样本自相关函数分析(ACF)或样本偏自相关函数分析(PACF)对模型滞后阶数进行初步判定,之后再通过最小信息准则判断赤池信息量准则(Akaike Information Criterion,AIC)值、施瓦茨信息准则(Schwarz Information Criterion,SIC)值和汉南-奎因准则(Hannan-quinn Criterion,HQ)值,选出最优阶数。
(4) 模型检验。通过白噪声检验、残差自相关性检验、异方差检验、系数显著性检验,验证模型的有效性。
(5) 模型应用。对未来一段时间的O3浓度进行预测。
1.2.2 GARCH模型回归分析的一个重要前提是残差具有方差齐性。采用日数据或周数据的应用常常出现扰动项μt的条件方差σt2依赖于很多时刻之前变化量的情况,即可能会出现某种波动率聚集现象,最终反映为O3浓度在某个峰值或谷值出现之后一段时间内,连续出现高值或低值的异方差现象。这种现象在大气污染监测中较常见。异方差的存在,会极大影响回归方程的正确建立和统计推断。因此1982年恩格尔(Engle R.)提出自回归条件异方差模型(Autoregressive Conditional Heteroscedasticity Model,ARCH),并由博勒斯莱文(Bollerslev T.)在1986年发展成为广义自回归条件异方差模型(Generalized ARCH,简称GARCH)。GARCH(1, 1)模型的基本结构如下:
| $ \begin{array}{*{35}{l}} \sigma _{t}^{2}\text{=C}+\alpha \varepsilon _{t-1}^{2}+\beta \sigma _{t-1}^{2}, \\ {{y}_{t}}={{x}_{t}}\pi +{{\varepsilon }_{t}}{{\ }_{{}^\circ }} \\ \end{array} $ |
当期的方差依赖于3个因素,即常数项C,ARCH项εt-12(用前一期残差的平方表示,反映前一期的波动性)和GARCH项σt-12(前一期方差的预测值)。GARCH模型实际上是在ARCH模型的基础上,增加考虑了异方差函数的m阶自相关性而形成;它可以有效地拟合具有长期记忆性的异方差函数[16]。
GARCH模型的建立步骤:
(1) 检验ARCH效应。在建立ARMA模型后,使用拉格朗日乘数法(LM法)或残差平方自相关函数分析图检验其是否存在ARCH效应,若存在ARCH效应则进入下一步。
(2) 识别滞后阶数,选取最优模型。通过对比各模型系数的显著性与AIC、SIC、HQ值确定滞后阶数后,选取最合适的模型进行建模。
(3) 复验ARCH效应。建立模型后仍然使用LM法或残差平方自相关函数分析图检验其是否仍存在ARCH效应,若仍存在ARCH效应,则返回上一步调整模型阶数。
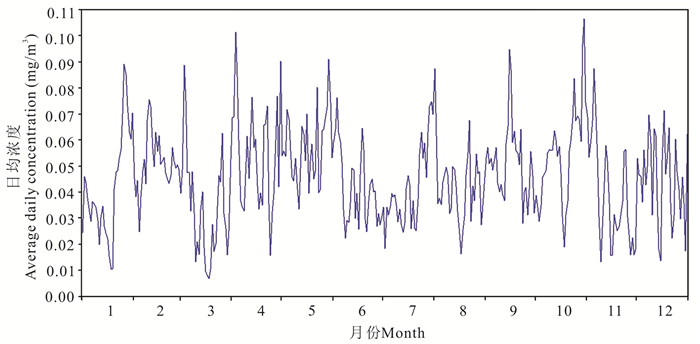
2 结果与分析 2.1 ARMA建模研究 2.1.1 数据预处理使用Eviews软件对南宁市2017年1月1日至2017年12月31日日均O3浓度监测值样本数据进行模型参数估计,并根据监测值样本数据构建时序图,从图 2可初步判断O3序列非线性近似平稳,因此无法确定其有周期性、趋势性。为确定该序列的平稳性,对其进行平稳性检验并使用Augmented Dickey-Fuller (ADF)单位根检验方法判断。
|
| 图 2 2017年O3日均浓度时序图 Fig. 2 Sequence diagram of average daily concentration of O3 in 2017 |
检验结果表明(表 1和表 2),ADF的t统计量(-8.244 276)小于1%显著水平下的临界值(-3.983 471),可认为O3样本序列在1%的显著水平下属于不含单位根的平稳过程,趋势项(TREND)系数的P值大于0.05,可认为趋势项系数显著为零。常数项C系数P值小于0.05,表示常数项显著不为零。即该O3样本序列为带有常数项、不含趋势项、滞后阶数为0的平稳序列。
| t统计量 t-statistic |
P值 Prob. |
1%显著水平下检验关键值 Test critical values at 1% level |
5%显著水平下检验关键值 Test critical values at 5% level |
10%显著水平下检验关键值Test critical values at 10% level |
| -8.244 276 | 0 | -3.983 471 | -3.422 218 | -3.133 955 |
| 变量 Variable |
系数 Coefficient |
标准差 Standard error |
t统计值 t-statistic |
P值 Prob. |
| O3(-1) | -0.316 002 | 0.038 330 | -8.244 276 | 0.000 0 |
| 常数项C | 0.014 593 | 0.002 235 | 6.530 066 | 0.000 0 |
| 趋势项(TREND) | 0.000 000 425 | 0.000 006 59 | 0.064 434 | 0.948 7 |
2.1.2 模型识别
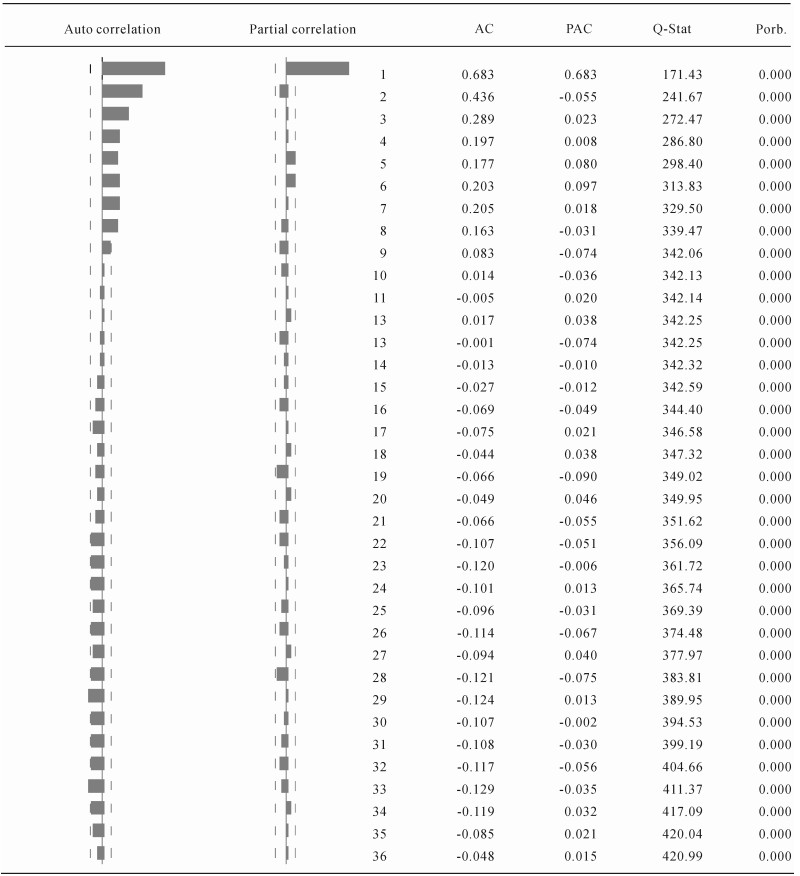
证明O3序列平稳之后,通过自相关函数分析初步为ARMA模型定阶(表 3)。
观察表 3发现自相关函数分析图拖尾,偏自相关图一阶截尾,因此初步判断模型形式为ARMA(1, 0)。为确定模型形式与阶数,同时采用AIC、SIC和HQ方法,使用最小信息准则判断最佳阶数。从表 4可见,模型ARMA(1, 0)在SIC和HQ中信息最小,在AIC中仅此与ARMA(1, 1)为次佳,综合判断, 模型ARMA(1, 0)为最佳阶数。
| 模型Model | AIC | SIC | HQ |
| ARMA(1, 0) | -5.813 072 | -5.791 659 | -5.804 561 |
| ARMA(1, 1) | -5.813 082 | -5.780 962 | -5.800 316 |
| ARMA(0, 1) | -5.647 139 | -5.625 769 | -5.638 646 |
| ARMA(2, 0) | -5.812 695 | -5.780 510 | -5.799 902 |
| ARMA(2, 1) | -5.808 003 | -5.765 089 | -5.790 945 |
| ARMA(2, 2) | -5.808 007 | -5.765 094 | -5.790 949 |
| ARMA(0, 2) | -5.751 998 | -5.719 944 | -5.739 259 |
| ARMA(1, 2) | -5.807 812 | -5.764 986 | -5.790 790 |
| 注:粗体为最大值 Note:Bold are the maximum | |||
2.1.3 ARMA模型检验
(1) 自相关检验
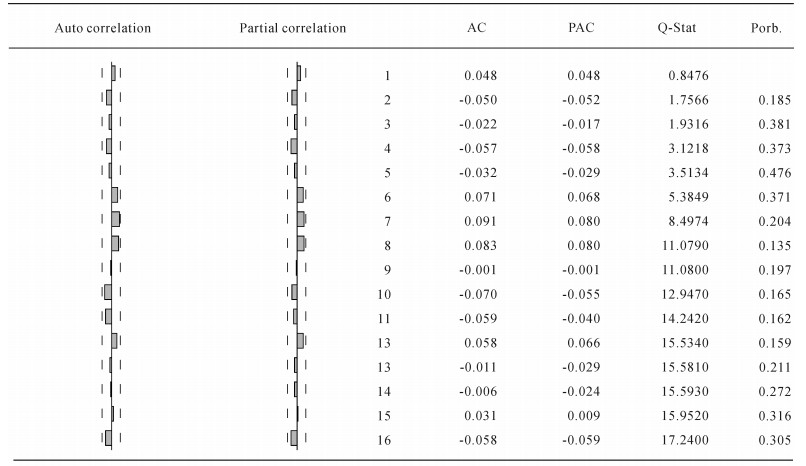
本研究采用残差序列相关LM法检验ARMA模型,选取滞后一至五阶进行残差相关检验。检验结果表明ARMA(1, 0)模型异方差怀特检验量对应的P值均大于0.05,即残差不存在序列相关,无遗漏变量,滞后阶数选取合理。
(2) 残差白噪声检验与正态检验
通过观察该样本残差序列的ACF、PACF,判断该残差序列是否为白噪声序列。
表 5显示,各期Q统计量对应P值均高于0.05,说明残差序列是白噪声序列。结合自相关检验与白噪声检验,判定ARMA(1, 0)模型已经将原序列中的信息提取完全,该模型拟合显著。
2.2 GARCH模型研究 2.2.1 GARCH模型的建立
对已建立的ARMA(1, 0)模型使用LM法检验判定模型是否具有ARCH效应,结果显示,F统计值为4.637 139,异方差怀特检验量(Obs*R-squared)为4.603 694,F统计量的概率(Prob.F (1, 391))为0.031 9,卡方检验的概率(Prob.Chi-Square(1))0.031 9。该结果表明模型存在1阶ARCH效应,因此需要建立GARCH模型去除ARCH效应。GARCH模型使用最小信息准则对比如表 6。由表 6可知GARCH模型滞后阶数(3, 2)最小,选择GARCH(3, 2)模型,模型AIC=-5.864 8、SC=-5.768 4、HQ=-5.826 5。
| GARCH | AIC | SC | HQ |
| (1, 1) | -5.826 0 | -5.761 8 | -5.800 5 |
| (1, 2) | -5.823 8 | -5.748 8 | -5.794 0 |
| (1, 3) | -5.848 7 | -5.763 1 | -5.814 7 |
| (2, 1) | -5.820 3 | -5.745 3 | -5.790 5 |
| (2, 2) | -5.817 2 | -5.731 5 | -5.783 1 |
| (2, 3) | -5.819 4 | -5.723 1 | -5.781 1 |
| (3, 1) | -5.817 2 | -5.731 5 | -5.783 1 |
| (3, 2) | -5.864 8 | -5.768 4 | -5.826 5 |
| (3, 3) | -5.843 3 | -5.736 3 | -5.800 8 |
| 注:粗体为最大值。 Note: Bold are the maximum. | |||
2.2.2 GARCH模型的检验
使用LM法检验GARCH(3, 2)模型残差是否仍具有ARCH效应,结果显示,其F统计值为0.059 821(P=0.806 9),异方差怀特检验量为0.060 143(P=0.806 3)。GARCH族模型异方差怀特检验量均大于显著水平0.05,残差序列不存在ARCH效应,因此此次研究建立的GARCH模型均满足序列平稳且没有ARCH效应的统计要求。
2.3 模型预测效果对比结合前文基于南宁市2017年1月1日-2017年12月31日O3日均浓度监测值样本数据建立的ARMA(1, 1)模型-GARCH(3, 2)模型,对南宁市2018年1月1日至2018年1月31日O3日均浓度进行预测,结合实测值进行误差分析(图 3)。
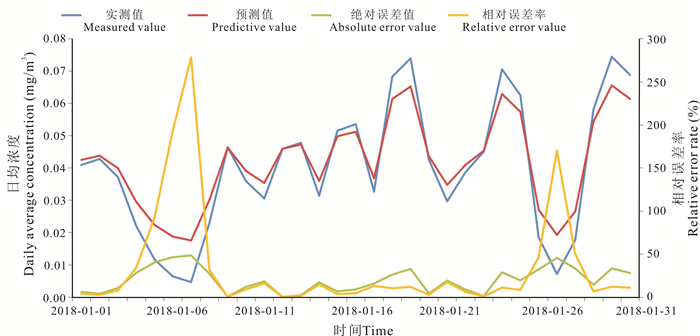
|
| 图 3 模型拟合效果图 Fig. 3 Chart of model fitting effect |
结果表明,模型预测值与实测值的拟合趋势基本一致,相对误差率平均34.39%;在31 d预测浓度值中,有9 d与实测值相对误差率在5%以内,有14 d与实测值相对误差率在10%以内,有9 d与实测值相对误差率在10%-20%,但也有8 d预测值与实测值误差较大。从图 3可以看出,在实测值拟合曲线峰、谷值等前后位置容易出现较大误差。2018年1月1日与1月2日的预测值相对误差率均不超过4%,说明由于时间序列模型体现的是时间序列的自相关性和自身的动态记忆性,更适宜反映样本时间序列的短期变化。
3 结论本文通过构建ARMA-GARCH模型,对南宁市城区2018年1月31 d的O3日均浓度进行预测,预测值拟合曲线基本能与实测值保持一致。在31 d预测浓度值中,23 d预测相对误差率在20%,较为准确,其中2018年1月1日与1月2日相对误差率均小于4%。这表明采用时间序列ARMA-GARCH模型短期预测O3浓度是比较有效的,能为O3浓度的预测预报提供一定的参考价值。
尽管时间序列ARMA-GARCH模型描述的是样本在时间序列上的自相关性,可较为准确地反映短期内的时间序列变化关系,而非长期的变化关系。但正因如此,时间序列ARMA-GARCH模型更适宜应用在短期大气污染物浓度预测方面,充分发挥其速度快、准确性较高的特点,为大气污染防治提供决策参考。
| [1] |
秦瑜, 赵春生. 大气化学基础[M]. 北京: 气象出版社, 2003: 85-86.
|
| [2] |
BINKOWSKI F S, ROSELLE S J. Models-3 community multiscale Air Quality (CMAQ) model aerosol component 1.Model description[J]. Journal of Geophysical Research:Atmospheres, 2003, 108(D6): 4183. |
| [3] |
TIE X X, GENG F H, PENG L, et al. Measurement and modeling of O3 variability in Shanghai, China:Application of the WRF-Chem model[J]. Atmospheric Environment, 2009, 43(28): 4289-4302. DOI:10.1016/j.atmosenv.2009.06.008 |
| [4] |
THOMPSON M L, REYNOLDS J, COX L H, et al. A review of statistical methods for the meteorological adjustment of tropospheric ozone[J]. Atmospheric Environment, 2001, 35(3): 617-630. |
| [5] |
LU W Z, WANG D. Ground-level ozone prediction by support vector machine approach with a cost-sensitive classification scheme[J]. Science of the Total Environment, 2008, 395(2/3): 109-116. |
| [6] |
COMAN A, IONESCU A, CANDAU Y. Hourly ozone prediction for a 24-h horizon using neural networks[J]. Environmental Modelling & Software, 2008, 23(12): 1407-1421. |
| [7] |
YI J, PRYBUTOK V R. A neural network model forecasting for prediction of daily maximum ozone concentration in an industrialized urban area[J]. Environmental Pollution, 1996, 92(3): 349-357. DOI:10.1016/0269-7491(95)00078-X |
| [8] |
蔡旺华. 运用机器学习方法预测空气中臭氧浓度[J]. 中国环境管理, 2018, 10(2): 78-84. |
| [9] |
张建同, 尤建新. 非线性时序法在城市大气污染预测中的应用[J]. 自然灾害学报, 2007, 16(3): 96-99. DOI:10.3969/j.issn.1004-4574.2007.03.018 |
| [10] |
程文娜. PM10浓度的时间序列模型及预测[J]. 科学技术与工程, 2010, 10(9): 2260-2262. DOI:10.3969/j.issn.1671-1815.2010.09.051 |
| [11] |
徐辉军, 张林男. 基于GM-ARMA组合模型的PM2.5浓度预测——以扬州市为例[J]. 南通职业大学学报, 2018, 32(4): 67-71. DOI:10.3969/j.issn.1008-5327.2018.04.017 |
| [12] |
喻彩丽.基于空气质量时间序列分析的预测模型设计与应用[D].银川: 宁夏大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10749-1016267970.htm
|
| [13] |
赵文霞, 秦志英, 马玲. 石家庄市道路交通环境NOx污染水平及ARMA模型预测[J]. 环境工程学报, 2014, 8(7): 2952-2956. |
| [14] |
高铁梅. 计量经济分析方法与建模[M]. 北京: 清华大学出版社, 2009: 126.
|
| [15] |
庞皓. 计量经济学[M]. 3版. 北京: 科学出版社, 2014: 240-244.
|
| [16] |
张晓峒. 计量经济学软件eviews使用指南[M]. 天津: 南开大学出版社, 2003: 212.
|