模型验证是确定河口海岸模型的模拟结果能否有效地模拟真实物理过程并进一步应用的最重要步骤。可视化方法一般是指将潮位、潮流、盐度、含沙量等模拟数据和实测数据针对某一参量(如时间)绘制于同一图中,进而比较二者的符合程度,判断模拟结果是否达到要求。此方法已广泛应用于海洋模拟[1-3]。然而仅通过图形,实测数据和模拟数据之间并没有明确的定量化比较,在某种程度上这种方法也是基于验证者的主观判断。由于人们通常把每个模拟数据点的偏差看作是该点与实测数据曲线的最近距离[4],所以一个看似令人满意的模拟结果很可能包含相当大的误差。一些量化指标如均方根误差、平均绝对误差等,计算了每一对模拟数据与实测数据之间的偏差。这些方法直接给出了模拟的效果,但在使用这些方法时也存在一些不足。相关系数也常用于河口海岸模型的验证,它给出了模拟数据和实测数据之间的相关性,但不能量化误差的大小。目前,相关系数多与其他量化指标共同使用。Skill是一个常用的模型验证指标,一般与相关系数或均方根误差同时使用,是目前应用最为广泛的验证方法[2-3]。然而在实际应用中,Skill值的变幅相当大,其值也不能直观表示误差的大小。此外,Skill并无明确的表征模拟结果可接受的阈值。统计检验在河口海岸模型验证中的应用不多。在河口海岸模型验证中,若将模拟数据和实测数据分别作为横纵轴画于一图,如果二者之间没有偏差,那么数据点将位于直线y=x上[5]。由于模拟数据不可能完全与观测数据一致,所以需要对这些数据点进行回归分析以衡量模拟的效果。R检验、t检验及F检验对于一元线性回归的显著性检验具有相同的效果,可用来检验拟回归模型的线性显著性[6]。本文首先对目前常用的模型验证指标的性能及敏感性进行比较。在此基础上,对统计检验方法进行了归纳和扩展,给出了基于统计检验的模型验证方法。结果显示该方法对量化模型数据的误差具有很好的适应性和准确性。
1 常用的模型验证量化指标在河口海岸模型验证中,最常用的量化指标包括均方根误差(RMSE)、平均误差(MAE)平均相对误差(MA%E)等[4]。Willmott[7]给出的Skill是目前河口海岸模型中应用最为广泛的量化指标。
| $ RMSE = \sqrt {\sum {\frac{{{{\left( {{x_{oi}} - {x_{mi}}} \right)}^2}}}{n}} } , $ | (1) |
| $ MAE = \frac{{\sum {\left| {{x_{oi}} - {x_{mi}}} \right|} }}{n}, $ | (2) |
| $ MA\% E = \frac{{\sum {\left| {{x_{oi}} - {x_{mi}}} \right|} /{x_{oi}}}}{n}, $ | (3) |
| $ Skill = 1 - \frac{{\sum\nolimits_{i = 0}^n {{{\left| {{x_{oi}} - {x_{mi}}} \right|}^2}} }}{{\sum\nolimits_{i = 0}^n {{{\left( {\left| {{x_{oi}} - {{\bar x}_o}} \right| + \left| {{x_{mi}} - {{\bar x}_o}} \right|} \right)}^2}} }}, $ | (4) |
式(1)—(4)中,下标o、m分别代表实测和模拟,i为数据点号, 上划线代表时间平均。对于潮流流速的验证,Schnab等[8]和Beletsky等[9]给出了量化参数Fn:
| $ {\left\| {{{\vec u}_{oi}},{{\vec u}_{mi}}} \right\|_2} = {\left( {\frac{1}{n}\sum {{{\left| {{{\vec u}_{oi}} - {{\vec u}_{mi}}} \right|}^2}} } \right)^{\frac{1}{2}}}, $ | (5) |
| $ Fn = \frac{{{{\left\| {{{\vec u}_o},{{\vec u}_m}} \right\|}_2}}}{{{{\left\| {{{\vec u}_o},0} \right\|}_2}}}, $ | (6) |
其中式(5)为傅立叶测度(Fourier Norm)。Anderson等[10]给出了一系列的流速验证的参数指标,式(7)—(10),上划线代表时间平均。这些指标分别对应了不同的流速统计量。ε1量化了潮流的总流的模拟值与实测值之间的偏差,ε2和ε3分别量化潮流流速中周期性变化部分及余流部分的模拟误差,ε4为实测潮流和模拟潮流的动能比。
| $ {\varepsilon _1} = \frac{{\sum {\left[ {{{\left( {{u_o} - {u_m}} \right)}^2} + {{\left( {{v_o} - {v_m}} \right)}^2}} \right]} }}{{\sum {\left[ {{{\left( {{u_o}} \right)}^2} + {{\left( {{v_o}} \right)}^2}} \right]} }}, $ | (7) |
| $ \begin{array}{l} {\varepsilon _2} = \\ \frac{{\sum {\left[ {{{\left( {{u_o} - {{\bar u}_o} - {u_m} + {{\bar u}_m}} \right)}^2} + {{\left( {{v_o} - {{\bar v}_o} - {v_m} + {{\bar v}_m}} \right)}^2}} \right]} }}{{\sum {\left[ {{{\left( {{u_o} - {{\bar u}_o}} \right)}^2} + {{\left( {{v_o} - {{\bar v}_o}} \right)}^2}} \right]} }}, \end{array} $ | (8) |
| $ {\varepsilon _3} = \frac{{\left[ {{{\left( {{{\bar u}_o} - {{\bar u}_m}} \right)}^2} + {{\left( {{{\bar v}_o} - {{\bar v}_m}} \right)}^2}} \right]}}{{\left[ {{{\left( {{{\bar u}_o}} \right)}^2} + {{\left( {{{\bar v}_o}} \right)}^2}} \right]}}, $ | (9) |
| $ {\varepsilon _4} = \frac{{\sqrt {\sum {\left[ {{{\left( {{u_o}} \right)}^2} + {{\left( {{v_o}} \right)}^2}} \right]} } }}{{\sqrt {\sum {\left[ {{{\left( {{u_m}} \right)}^2} + {{\left( {{v_m}} \right)}^2}} \right]} } }}。$ | (10) |
将模拟数据和实测数据分别置于x轴和y轴,则可以通过线性回归得到直线:
| $ {{\hat y}_i} = a + b{x_i}\left( {i = 1,2,3, \cdots ,n} \right), $ | (11) |
其中a和b为线性回归参数。如果模型数据和观测数据完全符合,则a=0,b=1。回归方程的有效性可以通过假定检验(R检验、t检验或F检验,式(12)—(15))来评价。
R检验:
| $ R = \frac{{{S_{xy}}}}{{\sqrt {{S_{xx}}{S_{yy}}} }}, $ | (12) |
其中Syy=∑(yi-y)2, Sxx=∑(xi-x)2, Sxy=∑(xi-x)(yi-y)。对于置信水平α及样本容量n,如果
对于b,H0:b=1, H1:b≠1:
| $ t = \left( {b - \beta } \right)\frac{{\sqrt {\left( {n - 2} \right){S_{xx}}} }}{{\sqrt {{S_E}} }} \sim t\left( {n - 2} \right), $ | (13) |
对于a,H0:a=0, H1:a≠0:
| $ t = a\frac{{\sqrt {\left( {n - 2} \right)} }}{{\sqrt {\left( {\frac{1}{n} + \frac{{{{\bar x}^2}}}{{{S_{xx}}}}} \right){S_E}} }} \sim t\left( {n - 2} \right), $ | (14) |
其中
| $ \begin{array}{l} {F_D} = \\ \frac{{\left( {n - 2} \right)\left[ {n{{\left( a \right)}^2} + 2n{{\bar x}_m}\left( a \right)\left( {b - 1} \right) + \sum {x_{mi}^2} {{\left( {b - 1} \right)}^2}} \right]}}{{2n{{\left( S \right)}^2}}}, \end{array} $ | (15) |
其中xm为模型数据的平均值,S为标准方差。需要指出的是,该检验结果仅意味着线性关系是显著的,但不能确定此线性回归方程是一个合适的回归模型[11]。
这些统计检验并未给出误差的直接量化,而模型模拟的效果需要对模型数据的绝对误差或相对误差进行量化。如《海岸与河口潮流泥沙模拟技术规程》[12]中规定:高低潮位的误差小于0.1 m、涨落潮的平均流速误差小于10%。为了将统计检验与模型数据的误差联系起来,可采用一个新的验证流程,其基本思想是:对于式(11),若强制a=0进行回归,则回归直线的斜率代表了平均相对误差;若强制b=0进行回归,则回归直线的截距代表了平均绝对误差。
3 数值试验 3.1 数据构建为研究前述验证指标的性能,构建了两组时间序列过程。首先将潮位过程表示如下:
| $ {\zeta _o}\left( i \right) = A\cos \left( {\frac{{\rm{ \mathsf{ π} }}}{{12.5}}i} \right),i = 1,2,3, \cdots ,25, $ | (16) |
| $ \begin{array}{l} {\zeta _m}\left( i \right) = {\zeta _o}\left( i \right)\left( {1 + f \cdot Rand\left( i \right)} \right),i = 1,2,\\ 3, \cdots ,25, \end{array} $ | (17) |
其中:ζo(i)代表实测数据,振幅(A)为2 m,频率(ω=π/12.5 h),ζm(i)为模型数据。Rand(i)为-1.0~1.0的随机数序列。系数f用以控制误差的大小,变化范围为0.02~1.00。时间序列的长度是25 h。图 1给出了两个基于式(16)—(17)的时间序列过程。对于式(7)—(11)涉及的流速过程,将式(16)中的振幅A分别取1 m/s和0.2 m/s对应于潮流椭圆的长轴和短轴流速振幅。此外,为研究模型验证指标对模型数据中异常值的适应性,构建数据序列:
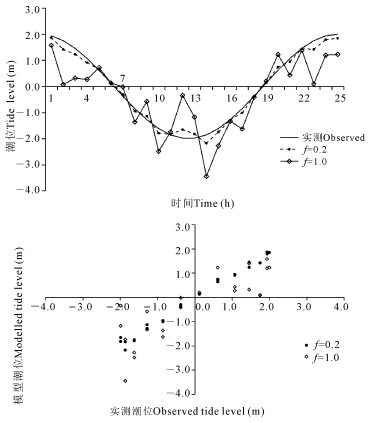
|
| 图 1 潮位实测数据和模拟数据示意图 Fig. 1 Schematic diagram of observed and simulated data for tide |
| $ {{\zeta '}_m}\left( i \right) = {\zeta _o}\left( i \right) + \delta \left( j \right)A,i,j = 1,2,3, \cdots ,25, $ | (18) |
其中:当j=i时,δ(j)=1;当j≠i时,当δ(j)=0。
3.2 敏感性分析基于3.1中数据序列,图 2给出了潮位和潮流的相关系数(CC)、Skill和均方根误差对于系数f的变化。在图 2a中,均方根误差随系数f线性增加,这跟此数值试验的假设是一致的。相关系数呈现单调递减的趋势。当系数f为0时相关系数为1;系数f为1时,相关系数为0.83。随着系数f的增加,相关系数的变幅越大。Skill的变化趋势与相关系数非常类似,当系数f从0逐渐增加到1时,Skill从1减小至0.89。系数f=1代表了平均相对误差约为50%,最大相对误差约为100%。所以可以看出,不论是相关系数还是Skill,其对误差的变化并不敏感。在模拟数据的误差相当大时,相关系数或Skill值仍可能出现较大的值。图 2b给出了基于前节所述方法构造的潮流流速数据计算的式(7)—(9)的值。可以看出,相关系数、Skill及均方根误差呈现与图 2b类似的变化趋势,相关系数与Skill分别由1减小至0.87和0.91。ε1的增加约为0.38至0.74, ε2增加约0.03至约0.35。事实上,对于不同的模型试验,由于其背景流速值(式(7)—(9)中的分母)变化很大,ε1和ε2在不同模型之间可能差别很大,ε1—ε4在不同模型间不具有可比性。
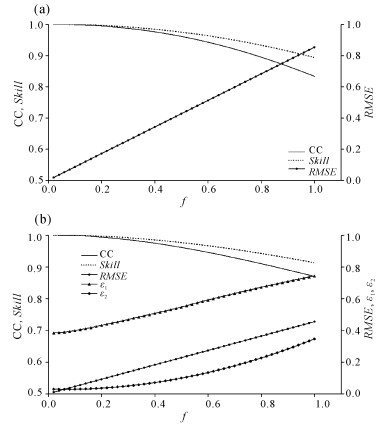
|
| 图 2 潮位(a)、流速(b)验证相关系数(CC)、Skill、均方根误差及ε1、ε2随f的变化 Fig. 2 Variations of tide level (a), velocity (b) verification correlation coefficient (CC), Skill, RMSE, ε1 and ε2 against factor f |
综合而言,Skill对偏差没有显著的敏感性。即使是系数f达到1.0,它的范围仍为1.0~0.9,相关系数也保持在1.0至0.8的区间。其他一些模拟显示的Skill和相关系数值可能小于上面的数值实验。如果随机数序列是均匀分布的,则当f=1时,平均误差约为50%。这说明虽然模拟数据和实测数据之间的偏差比较大,但是Skill与相关系数仍可能为很大的值。虽然不能据此断定小的Skill值一定意味着模拟不理想,但是在较大的误差情况下可能会有一个明显大的Skill,这可能会导致对模拟结果好坏的误判。在这个数值实验中,相关系数显示了实测数据和模拟数据序列之间的相关性,但是它不能量化误差,不能单独用于河口海岸模型验证。根据以上分析,Skill和相关系数可用于潮位,盐度,泥沙等标量验证,也可用于对比潮流的流速与流向,但使用Skill和相关系数的验证方法是否是一个合适的方法是需谨慎的。
3.3 统计检验方法 3.3.1 与误差直接计算方法的一致性如前所述,基于式(11)—(15)的方法不能与模拟数据的误差直接联系起来。若是预设式(11)中的截距(斜率),则斜率(截距)在一定意义上则代表了平均相对(绝对)误差。对于这两种情况,相应的斜率和截距可分别表示如下
| $ b = \frac{{\sum {{x_{oi}}} {x_{mi}}}}{{\sum {{x_{oi}}} }}, $ | (19) |
| $ a = \frac{{\sum {{y_i}} - \sum {{x_i}} }}{n}。$ | (20) |
利用式(13)、(14)对式(19)、(20)进行显著性检验,检验斜率(b)或截距(a)是否显著不为1或0。若在某个显著性水平α时检验通过,则b的置信区间可以表示为
| $ \begin{array}{l} \left( {{b_{low}},{b_{high}}} \right) = \\ \left( {b - {t_{\frac{\alpha }{2}}}\frac{{\sqrt {{S_E}} }}{{\sqrt {\left( {n - 2} \right){S_{xx}}} }},b + {t_{\frac{\alpha }{2}}}\frac{{\sqrt {{S_E}} }}{{\sqrt {\left( {n - 2} \right){S_{xx}}} }}} \right), \end{array} $ | (21) |
其中,blow和bhigh分别为置信区间的上、下限。当截距预设为0时,(b-1)则代表了平均相对误差。最大相对误差可定义为
| $ \begin{array}{l} {E_b} = Max\left( {Abs\left( {{b_{low}} - 1} \right),Abs\left( {{b_{high}} - 1} \right)} \right) \times \\ 100\% , \end{array} $ | (22) |
其中Max和Abs分别为最大值和绝对值。类似的,对于预设斜率b=1的情况,截距a的置信区间可表示为
| $ \begin{array}{l} \left( {{a_{low}},{a_{high}}} \right) = \\ \left( {a - {t_{\frac{\alpha }{2}}}\frac{{\sqrt {\left( {\frac{1}{n} + \frac{{{{\bar x}^2}}}{{{S_{xx}}}}} \right){S_E}} }}{{\sqrt {\left( {n - 2} \right)} }},a + {t_{\frac{\alpha }{2}}}\frac{{\sqrt {\left( {\frac{1}{n} + \frac{{{{\bar x}^2}}}{{{S_{xx}}}}} \right){S_E}} }}{{\sqrt {\left( {n - 2} \right)} }}} \right), \end{array} $ | (23) |
类似式(22),最大绝对误差可定义为
| $ {E_a} = Max\left( {Abs\left( {{a_{low}}} \right),Abs\left( {{a_{high}}} \right)} \right)。$ | (24) |
利用3.1中生成的数据对式(19)—(24)进行数值试验。计算结果如图 3和表 1所示。其中相对误差和绝对误差的阈值分别设为10%和0.1 m。
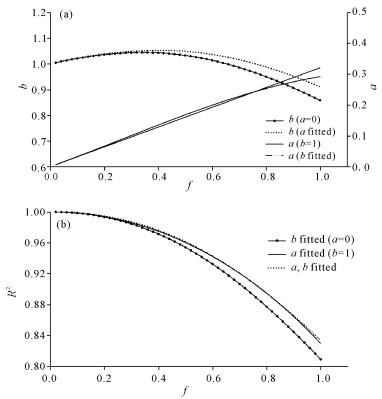
|
| 图 3 斜率b和截距a(a),决定系数R(b)随f的变化 Fig. 3 Variations of slope b and intercept (a) and coefficient of determination R (b) against factor f |
| 试验1 Test 1 |
试验2 Test 2 |
试验3 Test 3 |
试验4 Test 4 | 试验5 Test 5 | ||||
| α=0.05 | α=0.01 | α=0.05 | α=0.01 | |||||
| 接受域 Acceptance region |
全域 All region |
全域 All region |
全域 All region |
f≤0.22 | f≤0.18 | RMSE≤0.12 m | RMSE≤0.10 m | |
| 拒绝域 Rejection region |
- | - | - | f>0.22 | f>0.18 | RMSE>0.12 m | RMSE>0.10 m | |
图 3a中,对于a和b均拟合(Fitted)的情况,在f为0.4左右时,斜率b达到最大,约为1.05;当系数f为1时,b约为0.91。截距a随着f的增加而单调增加,从0增至约0.29。当a预设为0时,b的变化呈现与之前明显的差异:当f小于0.3时,b几乎与a和b均拟合的情况相同;当f大于0.3时,随着f的增大,二者差异增大。当系数f为1时,b约为0.81。当b的预设为1时,a的值与a和b均拟合的情况非常接近。图 3b给出了决定系数(R2)随f的变化。a和b均拟合的情况与当b预设为1的情况,R2几乎是一致的,二者明显大于预设a=0情况下的R2。但总体而言,所有的R2都大于0.8。
表 1给出了相关统计检验的结果。将实测数据和模拟数据画于同一图中,横轴和纵轴分别代表实测数据和模拟数据。线性拟合后,首先利用R检验,F检验和t检验线性关系的显著性进行检验(试验1)。而后,利用式(13)和(14)检验b是否显不等于1(试验2)以及a是否显著不同于0(试验3)。结果表明,无论置信水平为0.05或0.01,即使系数f达到一个相当大的值,这些检验都能通过。在此基础上,按式(22)或式(24)计算统计意义上的最大的相对误差和绝对误差;进一步将区间限与判断模拟结果是否可接受的阈值进行比较并判定模拟结果是否可接受。在给定显著水平(α=0.05, 0.01)的情况下,试验4是针对阈值为10%的检验。在试验4中,当α=0.05时f的临界值为0.22,当α=0.01时f的临界值为0.18。f值平均约为0.20,这意味着20%的最大误差。如果误差是均匀分布的,那么也意味着10%的平均误差。试验5是针对绝对误差取阈值为0.1 m的检验。在试验5中,对于α=0.05和α=0.01,RMSE的临界值分别为0.12 m和0.10 m,与假设的阈值近似一致。由于表 1中的结果具有统计意义,计算得到的临界值并不等于严格等于预设的阈值。据此试验,可以认为α=0.05和α=0.01都是可接受的显著性水平。
3.3.2 对异常数据的包容性为检验前述统计检验方法对异常数据的包容性,利用式(19)得到的数据对式(21)—(22)进行计算。在该数据序列中,只有某一数据点(j点)增大一个振幅,其他值保持不变。这种情况下,如果采用最大相对误差或最大绝对误差都会得到模型结果不可接受的结论。即使是均方根误差,亦达到0.4 m。对于置信水平α=0.05和α=0.01,式(24)得到的最大统计误差约为0.25 m和0.31 m,远小于式(19)数据序列直接计算的最大误差。与均方根误差相比,亦明显较小。可以认为,此统计检验方法虽不能自动识别和剔除异常数据点,但对其导致的干扰具有明显的弱化效果。
3.3.3 在瓯江模型中的应用图 4为瓯江口北口七里港附近某测点2005年6月洪季的一次实测的流速和流向过程与物理模型试验结果的对比。在此,对流速和流向过程分别应用式(21)—(24)。表 2给出了相关统计量的值。由图 4可以看出,流向过程模型值偏小,流速过程在直观上符合较好。如前所述,由于每个点的偏差常被直观看做是模型点与实测数据线的最近距离,所以看似令人满意的模拟结果可能包含相当大的误差。表 2列出了相关系数、Skill等指标的计算值。对于流速,相关系数和Skill分别为0.975和0.987。一般而言,这样的数值已可以表征很好的符合度。然而,平均误差和均方根误差分别为0.24 m/s和0.29 m/s,最大误差甚至达到0.78 m/s。可见,虽然由相关系数和Skill判断,模型结果是可以接受的,但是平均误差约为20%,远大于《海岸与河口潮流泥沙模拟技术规程》[12]所规定的阈值10%。流向的结果与流速过程类似。结合3.2节的相关系数和Skill对误差的敏感性分析,可以认为采用相关系数结合Skill量化模型的验证效果存在一定的不准确性。表 2中同时列出了基于式(21)—(24)所得统计误差的计算结果。当α=0.05时绝对统计误差为0.15 m/s,相对统计误差为12.9%。由于统计误差要求是在某个置信水平下误差的区间范围,因此就数值上直观而言,统计误差的值比直接计算误差似乎表明模拟结果具有更好的符合性。针对更多数据的检验尚待后续研究。此外,值得注意的是,前述统计误差的计算方法及其对于流速或潮位过程得出的结论对于流向过程不一定适用,这是由于往复流的流向误差的分布与潮位或流速误差的分布不同,转流时的误差(图 4第2个数据点)可能导致误差的分布不满足正态分布假设。利用统计误差对旋转流流向进行验证尚待进一步的研究。
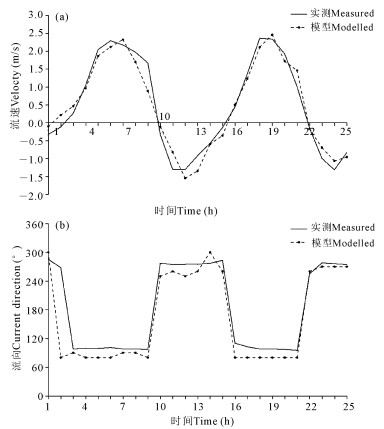
|
| 图 4 流速(a)和流向(b)的实测与模型试验的数值对比 Fig. 4 Measured numerical comparison of flow velocity (a) and flow direction (b) with model test |
| 项目 Item |
最大误差 Maximum error |
MAE | RMS | CC | Skill | 相对统计误差(%) Relative statistical error (%) |
绝对统计误差(m/s) Absolute statistical error (m/s) |
|||
| α=0.05 | α=0.01 | α=0.05 | α=0.01 | |||||||
| 流速 Velocity |
0.78 m/s | 0.24 m/s | 0.29 m/s | 0.975 | 0.987 | 12.9 | 16.5 | 0.15 | 0.19 | |
| 流向 Direction |
188° | 23° | 41° | 0.92 | 0.949 | |||||
4 结论
本文基于数值试验对一系列河口海岸模型验证方法进行了总结和比较。之后,对统计检验方法进行了分析和扩展。结果表明,即使模型误差显著,Skill和相关系数也可能得出较大的量值,这将导致模拟数据和实测数据符合良好的错误结论,最小二乘回归拟合的判定系数对误差的响应也不明显。统计检验是模型验证中的一种有效方法。针对斜率(b)和截距(a)的一般统计检验,如R检验,t检验和F检验,只检验线性关系的显著性而不是量化误差。当预设截距为0或斜率为1时,最小二乘拟合的系数可用于估计相对误差或绝对误差。统计误差于直接计算的误差具有一定的一致性,但比直接计算的误差更稳定。由于往复流流向的误差不一定满足正态分布假设,统计检验法对其不适用。
| [1] |
PURKIANI K, BECHERER J, FLÖSER G, et al. Numerical analysis of stratification and destratification processes in a tidally energetic inlet with an ebb tidal delta[J]. Journal of Geophysical Research:Oceans, 2015, 120(1): 225-243. DOI:10.1002/2014JC010325 |
| [2] |
GRÄWE U, FLÖSERLÖSER G, GERKEMA T, et al. A numerical model for the entire Wadden Sea:Skill assessment and analysis of hydrodynamics[J]. Journal of Geophysical Research:Oceans, 2016, 121(7): 5231-5251. DOI:10.1002/2016JC011655 |
| [3] |
LIN W B, WANG Y G, RUAN X H, et al. Modeling residual circulation and stratification in Oujiang river estuary[J]. China Ocean Engineering, 2012, 26(2): 351-362. DOI:10.1007/s13344-012-0027-z |
| [4] |
MAYER D G, BUTLER D G. Statistical validation[J]. Ecological Modelling, 1993, 68(1/2): 21-32. |
| [5] |
DENT J B, BLACKIE M J, HARRISON S R. Systems simulation in agriculture[M]. US, Barking: Applied Science Publishers, 1979.
|
| [6] |
周纪芗, 茆诗松. 概率论与数理统计[M]. 第3版. 北京: 中国统计出版社, 2007.
|
| [7] |
WILLMOTT C J. On the validation of models[J]. Physical Geography, 1981, 2(2): 184-194. DOI:10.1080/02723646.1981.10642213 |
| [8] |
SCHWAB D J, CLITES A H, MURTHY C R, et al. The effect of wind on transport and circulation in lake St.Clair[J]. Journal of Geophysical Research Atmospheres, 1989, 94(C4): 4947-4958. DOI:10.1029/JC094iC04p04947 |
| [9] |
BELETSKY D, SCHWAB D J. Modeling circulation and thermal structure in Lake Michigan:Annual cycle and interannual variability[J]. Journal of Geophysical Research:Oceans, 2001, 106(C9): 19745-19771. DOI:10.1029/2000JC000691 |
| [10] |
ANDERSON E J, SCHWAB D J. Relationships be-tween wind-driven and hydraulic flow in Lake St.Clair and the St.Clair River Delta[J]. Journal of Great Lakes Research, 2011, 37(1): 147-158. DOI:10.1016/j.jglr.2010.11.007 |
| [11] |
王惠文. 偏最小二乘回归方法及其应用[M]. 北京: 国防工业出版社, 1999.
|
| [12] |
中华人民共和国交通运输部天津水运工程科学研究所.海岸与河口潮流泥沙模拟技术规程[S].北京: 人民交通出版社, 2010.
|


