0 引言

近几年来，由配备有限电池的低功耗设备构成的、通过射频信号进行能量捕获的无线网络受到广泛的关注。针对基于射频信号的能量捕获无线网络(Radio frequency-based energy harvesting wireless networks，RF-EHWN)^[1]，目前的研究主要分为两个方向：一是无线信息与能量的同时传输(Simultaneous wireless information and power transfer，SWIPT)，二是无线供电的通信网络(Wireless powered communication networks，WPCN)。SWIPT关注的是接收端如何制定接收策略来权衡能量捕获和信息接收两个互斥的需求，分为时分切换(Time-switching)和功率分流(Power-splitting)两种方式^[2]。WPCN关注的是单发送端多接收端网络模型下，下行链路捕获到的能量用于上行链路的信息传输。如何制定发送端的发送策略来权衡各用户的上行吞吐量的公平性与最大化^[3]是WPCN研究的热点问题。

目前，SWIPT研究重点主要是接收端的操作策略，大部分研究工作都集中在点对点的单输入单输出系统(Single-input single-output，SISO)信道上。针对不存在同信道干扰的情况，Zhang等^[2]提出时分切换策略和功率分流策略。Zhou等^[3]将Zhang等^[2]提出的功率分流策略扩展为一个动态的功率分流策略，即动态地将射频(Radio frequency，RF)信号随时间以任意比例分成两个流。Zhou^[4]还设计一种非自适应和自适应的功率分流方案，并证明这两种方案都能提供最优解。Ju等^[5]从用户公平性的角度出发，提出一个“共同吞吐量”的性能指标，保证所有用户的传输速率完全相同。Liu等^[6]提出一个基于功率分流的SISO操作策略：在衰落信道增益超过某一阈值时，将所有接收到的信号按照固定比例进行分流，否则将所有信号都分流给信息接收。Liu等^[7]还提出一种基于瞬时信道增益和干扰功率的机会最优时间切换策略，以提高发送功率控制与接收端操作策略的联合优化效率。针对存在同信道干扰的情况，Ng等^[8]考虑通过发射端的功率分流和相关的接收端操作来最大化信息传输的频谱效率(即bit/s/Hz)，并将该问题表述为非凸优化问题，提出了两个接近最优性能的、低复杂度的次优迭代算法，以实现复杂度和性能的平衡。Ng等^[9]对能效进行优化，将信息传输的能量效率最大化(即bit/Joule)的问题表述为多维非凸优化问题，提出一种基于对偶分解和一维搜索的迭代算法。

对于WPCN的研究，大部分是基于“捕获-传输”协议^[10]，将一个单位的通信过程划分为下行的能量传输与捕获和上行的信息传输与解码两个阶段。接收端首先从下行传输广播信号中捕获能量，然后使用捕获到的能量向接入点发送独立的上行传输信息，并且对上下行的时间分配进行联合优化以达到最大化系统吞吐量。Wang等^[11]研究一个具有同频干扰的多输入多输出(Multi-input multi-output，MIMO)下行链路系统，提出使用支持有限个接收端的块对角化预编码方法，并在下行发射功率和空闲用户能量捕获的限制下，最大化信息接收端吞吐量的功率分配，提出一种功率分配的二分搜索方法，并给出最优解存在的必要条件。Ju等^[12]针对具有完全和不完全自干扰消除的情况，分别提出最优和次优的时间、功率分配方案。Alemayehu等^[13]提出一种联合波束形成和资源分配方案，以最大化WPCN的最小容量，同时实现上行链路和下行链路信息传输。

用户协作是提高常规无线通信系统的容量、覆盖范围等性能的有效方式，人们把用户协作通信引入到SWIPT和WPCN系统中，开展相关研究^[14-16]。Ju等^[17]研究如何利用WPCN中的双用户合作来进一步提高网络吞吐量和用户公平性，合理地分配使用部分上行传输的时间和从下行捕获到的能量来帮助中继用户把信息发送到接入点(Access point，AP)，并提出通过联合优化时间和能量的分配来表征近、远用户协作的性能指标，即加权和速率(Weighted sum-rate，WSR)。Bi等^[18]考虑将混合型AP分解为能源节点(Energy node，EN)和接入点AP，通过优化EN和AP的位置来减轻双近远问题所带来的影响。Chen等^[19]在此基础上提出一种新的激励机制，以促进在WPCN中的用户积极参与协作过程。

现有的WPCN只考虑在下行链路中进行能量传输，没有考虑信息传输的需求。在很多应用场景中，信息需要双向传输(例如传感器网络中，下行发送操作指令信息)，因此将“捕获-传输”协议进行拓展，增加下行信息传输的功能是值得考虑的。本文综合考虑接收端、发射端以及两端之间传输协议，将下行无线信息、能量的同时传输与无线供电的通信网络结合起来，提出一种新的在强干扰蜂窝小区中进行能量与信息联合传输的串行设计方案，以实现基站与用户之间的下行能量传输与上下行双向信息传输，提高能量传输的性能。该方案在具有多天线的单基站和单天线的多用户的一般性网络模型中，考虑将SWIPT与WPCN相结合，赋予WPCN下行信息传输的能力，并分成上行、下行两个子问题，通过分别求解最优的上行功率分配和下行波束成形以及时间分配来最大化上下行最小的用户传输速率。

1 网络模型 1.1 网络模型构建思路

在具有多天线的单基站和单天线的多用户的一般性网络模型中，我们在模型的设计上考虑将SWIPT应用于WPCN的下行链路中，即让原本只用于能量传输的下行RF信号携带用户所需的数据信息，需要此数据信息的用户对接收到的RF信号进行信息解码，不需要此数据信息的用户对RF信号进行能量捕获。具体而言，在上行阶段，基站根据收集到的理想的信道状态信息(Channel state information，CSI)来确定各用户的上行能量需求，下行阶段在保证用户能够捕获到足够能量的约束下，通过优化能量与信息传输的时间分配比例和基站的波束成形向量，相对公平地最大化各用户的信息传输能力。其中在下行阶段采用SWIPT中的时分切换(Time switching)方式，将一个单位时间分成若干时隙，并分配给各个用户轮换地进行信息传输，当一个用户在其分配到的时隙进行信息传输时，其他所有用户捕获RF信号的能量。

考虑一个具有强小区间干扰的大规模MIMO系统的蜂窝网络：N个小区，每个小区中有1个配有M个天线的基站和K个配有单天线的用户。将每个小区内所有用户分为F个组，将一个时间单位T分为上行、下行两个阶段：上行阶段为用户向基站发射信号进行信息传输，各个小区间异频传输，不考虑小区间干扰; 下行阶段为基站向用户发射信号进行基于时分切换(Time switching)的SWIPT，其中同组用户具有相同的能量捕获与信息解码的时间分配，各个小区同频传输，具有较强的小区间干扰。

假设在上行阶段各用户发送的信息包括用于上行信道估计的导频，在下行阶段基站发送的信息包括其获得的完全的CSI以及根据信道互易性获得的下行信道估计，并且假设每个基站都可以与其他基站分享其所获得的CSI。在下行阶段，组内各个用户之间采用多载波技术，如正交频分复用技术(Orthogonal frequency division multiplexing，OFDM)。为研究方便，本文将每组用户简化为1个用户，即令F=K。为叙述方便，后文中用cell-i来表示下标为i的小区，用cell-k来表示下标为k的用户。

1.2 信道估计

在上行阶段，所有用户发送导频信号，随后各个基站进行信道估计，cell-i中的基站与cell-j中的用户之间的上行信道系数矩阵为$ {{G}^{(i, j)}}={{H}^{(i, j)}}{{({{B}^{(i, j)}})}^{\frac{1}{2}}}$。其中G^{(i, j)}是M×K矩阵，$ {{[{{G}^{(i, j)}}]}_{mk}}=g_{mk}^{(i, j)}$表示cell-i中基站第m个天线与cell-j中user-k间的上行信道系数，H^{(i, j)}是M×K矩阵，$ {{[{{H}^{(i, j)}}]}_{mk}}=h_{mk}^{(i, j)}\tilde{\ }CN\left( \text{ }0, 1 \right)$表示cell-i中基站第m个天线与cell-j中的user-k之间的上行独立瑞利衰落系数，B^{(i, j)}是K×K的对角阵，其对角元素b_k^{(i, j)}表示cell-i中基站与cell-j中的user-k之间信道的路径损耗。由于$g_{mk}^{(i, j)}=h_{mk}^{(i, j)}\cdot \sqrt{b_{k}^{(i, j)}} $，因此有$g_{mk}^{(i, j)}\tilde{\ }CN\left( 0, b_{k}^{(i, j)} \right) $。假设在一个时间单位内，信道系数不变，并在下一个时间单位依概率改变。根据信道互易性，下行信道矩阵为上行信道矩阵的共轭转置矩阵，即(G^{(i, j)})^H，其中g_k^{(i, j)}是矩阵G^{(i, j)}的第k列，表示cell-i中的基站与cell-j中的user-k之间的上行信道系数矢量。

1.3 小区内时间分配

对于每一个小区，将其所有用户根据其到本小区基站间的信道系数矢量分为F个组，cell-j中的user-k所在的分组f_k^(j)与其到本小区基站的信道系数矢量g_k^{(j, j)}满足映射：

$ f_{k}^{(j)}=\left\{\begin{array}{c}{1,\left\|g_{k}^{(i, j)}\right\|_{2} \in D_{1}^{(j)}} \\ {\vdots} \\ {F,\left\|g_{k}^{(i, j)}\right\|_{2} \in D_{F}^{(j)}}\end{array}\right., $

(1)

cell-j中的user-k在下行阶段的信息传输时间t_k^(j)与其所在的分组f_k^(j)满足映射：

$ t_{k}^{(j)}=\left\{\begin{array}{c}{\tau_{1}^{(j)} T, f_{k}^{(j)}=1} \\ {\vdots} \\ {\tau_{F}^{(j)} T, f_{k}^{(j)}=F}\end{array}\right., $

(2)

且有$\sum\limits_{f=1}^{K}{{}}\tau _{f}^{(j)}=1 $。如图 1所示，其中T为下行阶段的总时间，τ^UL为上行阶段的时间。在下行阶段，第f_k^(j)的用户在其被分配的时间t_k^(j)内对接收到的RF信号进行信息解码，而在其余时间内进行能量捕获。定义cell-j中的下行阶段时间分配矢量$ {{t}^{(j)}}={{\left[ \begin{matrix} t_{1}^{(\text{ }j)} & t_{2}^{(j)} & \ldots & t_{K}^{(\text{ }j)}\text{ } \\ \end{matrix} \right]}^{\text{T}}}$。由于对时间划分实际应用中是离散取值的，即一个单位时间只能被有限地等分，故t_k^(j)的取值范围实际上是有限个离散的取值，t^(j)的取值空间是有限个离散向量的集合，记为t^(j)∈T^K×1。

1.4 上行阶段

在上行阶段的时间τ^UL内，各小区内用户同时向本小区基站进行上行传输。若不考虑用户的跨小区移动，则可以通过小区间用户异频传输来避免小区间干扰，则cell-j中的基站接收到的基带信号为$ {{z}^{(j)}}={{G}^{(j, j)}}{{x}^{(j)}}+{{n}^{(j)}}$，其中$ {{x}^{(j)}}={{[\begin{matrix} \sqrt{p_{1}^{(\text{ }j)}}\cdot s_{1}^{\text{UL}(j)} & \sqrt{p_{2}^{(j)}}\cdot s_{2}^{\text{UL}(j)} & \ldots & \sqrt{p_{K}^{(\text{ }j)}}\cdot s_{K}^{\text{UL}(j)} \\ \end{matrix}]}^{\text{T}}},p_{k}^{(\text{ }j)}$为下行阶段cell-j中的user-k的发射功率，s_k^UL(j)~CN(0, 1)为cell-j中的user-k上传给基站的独立信息，n^(j)~CN(0_M×1, σ²·1_M×1)为环境噪声矢量。对于上行阶段的基站而言，各个用户同时发送信息，考虑采用复杂度较低的线性检测算法来进行检测。经线性检测器A^(j)检测到的信号为

$ {r^{(j)}} = {\left( {{A^{(j)}}} \right)^H}{G^{(j,j)}}{x^{(j)}} + {\left( {{A^{(j)}}} \right)^H}{n^{(j)}}, $

(3)

典型的线性检测算法有

$ (1)最大比合并({\rm{MRC}}):A^{(j)}=G^{(j, j)}, $

(4)

$ (2)迫零({\rm{ZF}}):A^{(j)}=G^{(j, j)}\left(\left(G^{(j, j)}\right)^{H} G^{(j, j)}\right)^{-1}, $

(5)

(3) 最小均方误差(MMSE) ^[20]：

$ \begin{array}{l} \;\;\;\;\;\;{A^{(j)}} = \\ {G^{(j,j)}}{\left( {{{\left( {{G^{(j,j)}}} \right)}^H}{G^{(j,j)}} + \frac{1}{{{p^{{\rm{UL}}}}}}{I_{K \times K}}} \right)^{ - 1}}, \end{array} $

(6)

其中MMSE算法中的p^UL为上行阶段各用户统一的发送功率，由于本文中上行阶段各用户的发送功率不同，需要对MMSE检测重新进行推导。

对于cell-j中的用户发送功率矩阵$ {{P}^{(j)}}=\text{diag}\left\{ \begin{matrix} p_{1}^{(\text{ }j)} & p_{2}^{(j)} & \ldots & p_{K}^{(\text{ }j)} \\ \end{matrix} \right\}$，MMSE检测器为

$ \begin{array}{l} 推导\;1:{A^{(j)}} = \left( {{G^{(j,j)}}{P^{(j)}}{{\left( {{G^{(j,j)}}} \right)}^H} + } \right.\\ {\sigma ^2}{I_{M \times M}}{)^{ - 1}}{G^{(j,j)}}{P^{(j)}}, \end{array} $

(7)

cell-j中的基站经线性检测器A^(j)检测到的cell-j中的user-k的信号为

$ \begin{array}{l} \;\;\;\;\;\;\;\;r_k^{(j)} = {\left( {a_k^{(j)}} \right)^H}g_k^{(j,j)}\sqrt {p_k^{(j)}} s_k^{(j)} + \\ {\left( {a_k^{(j)}} \right)^H}\sum\limits_{l = 1,l \ne k}^K {g_l^{(j,j)}} \sqrt {p_l^{(j)}} s_l^{{\rm{UL}}(j)} + {\left( {a_k^{(j)}} \right)^H}{n^{(j)}}, \end{array} $

(8)

其中a_k^(j)为矩阵A^(j)的第k列。

因此在上行阶段，cell-j中的基站通过检测器A^(j)接收到本小区内user-k的信号与干扰加噪声比(SINR)为

$ \begin{array}{l} \;\;\;\;\;\;{\rm{SINR}}_k^{{\rm{UL}}(j)} = \\ \frac{{{{\left| {{{\left( {a_k^{(j)}} \right)}^H}g_k^{(j,j)}} \right|}^2}p_k^{(j)}}}{{\sum\limits_{l = 1,l \ne k}^K {{{\left| {{{\left( {a_k^{(j)}} \right)}^H}g_l^{(j,j)}} \right|}^2}} p_l^{(j)} + \left\| {a_k^{(j)}} \right\|_2^2{\sigma ^2}}}。\end{array} $

(9)

根据香农公式，cell-j中的user-k的上行传输速率为

$ \begin{array}{l} \;\;\;\;\;\;\;\;R_k^{{\rm{UL}}(j)} = {\tau ^{{\rm{UL}}}} \cdot \\ {\log _2}\left( {\frac{{\sum\limits_{l = 1}^K {{{\left| {{{\left( {a_k^{(j)}} \right)}^H}g_l^{(j,j)}} \right|}^2}} p_l^{(j)} + \left\| {a_k^{(j)}} \right\|_2^2{\sigma ^2}}}{{\sum\limits_{l = 1,l \ne k}^K {{{\left| {{{\left( {a_k^{(j)}} \right)}^H}g_l^{(j,j)}} \right|}^2}} p_l^{(j)} + \left\| {a_k^{(j)}} \right\|_2^2{\sigma ^2}}}} \right)。\end{array} $

(10)

1.5 下行阶段

假设下行阶段小区间同频传输，即考虑小区间干扰，则cell-j中的user-k接收到的携带信息的基带信号为

$ \begin{array}{l} y_k^{(j)} = {\left( {g_k^{(j,j)}} \right)^H}{w^{(j)}}\sqrt {{q^{(i)}}} {s^{{\rm{DL}}(j)}} + \\ \sum\limits_{i = 1,i \ne j}^N {{{\left( {g_k^{\left( {i,j} \right)}} \right)}^{\rm{H}}}{w^{\left( i \right)}}\sqrt {{q^{\left( i \right)}}} {s^{{\rm{DL}}\left( i \right)}}} + n_k^{\left( j \right)}, \end{array} $

(11)

其中，q⁽ⁱ⁾为下行阶段cell-i中的基站的发射功率，w⁽ⁱ⁾为cell-i中基站的M×1的波束成形矢量，有$ \|{{w}^{(i)}}{{\|}_{2}}=1, {{s}^{\text{DL}(i)}}\tilde{\ }CN\left( \text{ }0, 1 \right)$为cell-i中的基站传输的信息，n_k^(j)~CN(0, σ²)为cell-j中的user-k的环境噪声，假设该噪声无法捕获。

1.5.1 下行能量传输

cell-j中的user-k捕获的能量为

$ \begin{array}{*{20}{c}} {e_k^{(j)} = \left( {1 - t_k^{(j)}} \right)\eta _k^{(j)} \cdot }\\ {\sum\limits_{i = 1}^N {{{\left| {\sqrt {{q^{(i)}}} {{\left( {g_k^{(i,j)}} \right)}^H}{w^{(i)}}} \right|}^2}} ,} \end{array} $

(12)

其中η_k^(j)为能量捕获效率，有0 < η_k^(j)≤1。

1.5.2 下行信息传输

cell-j中的user-k的下行信息传输速率为

$ \begin{array}{l} R_k^{{\rm{DL}}(j)} = t_k^{(j)} \cdot \\ {\log _2}\left( {\frac{{\sum\limits_{i = 1}^N {{q^{\left( i \right)}}{{\left| {{{\left( {g_k^{\left( {i,j} \right)}} \right)}^{\rm{H}}}{w^{\left( i \right)}}} \right|}^2}} + {\sigma ^2}}}{{\sum\limits_{i = 1,i \ne j}^N {{q^{\left( i \right)}}{{\left| {{{\left( {g_k^{\left( {i,j} \right)}} \right)}^{\rm{H}}}{w^{\left( i \right)}}} \right|}^2}} + {\sigma ^2}}}} \right)。\end{array} $

(13)

2 问题求解

整个问题求解可以分为上、下行两个子问题，其中上行阶段采用最小速率最大化的方法来求解各小区内各用户的上行发送最优功率，并作为参数输入到下行阶段的问题求解；而下行阶段同样采用最小速率最大化的方法，求解各小区内基站的波束成形矢量，求解各个用户的能量捕获与信息解码的时间分配矢量。下面给出这两个阶段问题求解的优化方法。

2.1 上行阶段优化

在上行阶段，对于j=1, 2, …, N，由于各个小区之间异频传输互不干扰，故可表述为N个独立的问题，即将cell-j中所有用户中最小的上行传输速率R_k^UL(j)最大化：

$ \begin{array}{l} \mathscr{P}_{UL1}^{\left( j \right)}:\mathop {{\rm{maximize}}}\limits_{p_k^{\left( j \right)}} \mathop {\min }\limits_{1 \le k \le K} \left\{ {R_k^{{\rm{UL}}\left( j \right)}} \right\}\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;\mathit{p}_k^{\left( j \right)} \le \mathit{p}_k^{\max \left( j \right)},\forall k \in \left\{ {1,2, \cdots ,K} \right\}。\end{array} $

(14)

因为对于给定的τ^UL，R_k^UL(j)=τ^UL·log₂(1+SINR_k^UL(j))为单调增函数，引入中间变量θ，问题可转化为

$ \begin{gathered} \mathscr{P}_{{\text{UL2}}}^{\left( j \right)}:\mathop {{\text{maximize}}}\limits_{{p^{\left( j \right)}},\theta } \theta \hfill \\ {\text{s}}.\;{\text{t}}.\;\theta \leqslant {\text{SINR}}_k^{{\text{UL}}\left( j \right)},\forall k \in \left\{ {1,2, \cdots ,K} \right\}, \hfill \\ {p^{\left( j \right)}} \preccurlyeq {p^{\max \left( j \right)}} \hfill \\ \end{gathered} $

(15)

其中$ {{p}^{(j)}}=\text{ }{{\left[ \begin{matrix} p_{1}^{(\text{ }j)} & p_{2}^{(j)} & \ldots & p_{K}^{(\text{ }j)} \\ \end{matrix} \right]}^{\text{T}}}, {{p}^{\text{max }(j)}}={{\left[ \begin{matrix} p_{1}^{\text{max }(j)} & p_{2}^{\text{max }(j)} & \ldots & p_{K}^{\text{max }(j)} \\ \end{matrix} \right]}^{\text{T}}}, p_{k}^{\max (j)}$为cell-j中的user-k的上行最大功率。对于ZF、MRC、MMSE 3种检测方法，SINR_k^UL(j)对应有3种表述形式，问题$ \mathscr{P}_{\text{ULI}}^{(j)}$可分别转化$\mathscr{P}_{\text{UL-ZF}}^{(j)}, \mathscr{P}_{\text{UL-MRC}}^{(j)}, \mathscr{P}_{\text{UL-MMSE}}^{(j)}$，即：

$ \begin{gathered} \mathscr{P}_{{\text{UL - ZF}}}^{\left( j \right)}:\mathop {{\text{maximize}}}\limits_{{p^{\left( j \right)}},\theta } \theta \hfill \\ {\text{s}}.\;{\text{t}}.\;\theta \leqslant \frac{1}{{{{\left[ {{{\left( {{{\left( {{G^{\left( {j,j} \right)}}} \right)}^H}{G^{\left( {j,j} \right)}}} \right)}^{ - 1}}} \right]}_{kk}}}} \cdot \hfill \\ \frac{{p_k^{\left( j \right)}}}{{{\sigma ^2}}},\forall k \in \left\{ {1,2, \cdots ,K} \right\} \hfill \\ {p^{\left( j \right)}} \preccurlyeq {p^{\max \left( j \right)}} \hfill \\ \end{gathered}, $

(16)

$ \begin{gathered} \mathscr{P}_{{\text{UL - MRC}}}^{\left( j \right)}:\mathop {{\text{maximize}}}\limits_{{p^{\left( j \right)}},\theta } \theta \hfill \\ {\text{s}}.\;{\text{t}}.\;\theta \leqslant \frac{{\left\| {g_k^{\left( {j,j} \right)}} \right\|_2^2p_k^{\left( j \right)}}}{{\sum\limits_{l = 1,l \ne k}^K {\frac{{{{\left| {{{\left( {g_k^{\left( {j,j} \right)}} \right)}^{\text{H}}}g_l^{\left( {j,j} \right)}} \right|}^2}}}{{\left\| {g_k^{\left( {j,j} \right)}} \right\|_2^2}}p_l^{\left( j \right)}} + {\sigma ^2}}}, \hfill \\ \forall k \in \left\{ {1,2, \cdots ,K} \right\} \hfill \\ {p^{\left( j \right)}} \preccurlyeq {p^{\max \left( j \right)}}, \hfill \\ \end{gathered} $

(17)

$ \begin{gathered} \mathscr{P}_{{\text{UL - MMSE}}}^{\left( j \right)}:\mathop {{\text{maximize}}}\limits_{{p^{\left( j \right)}},\theta } \theta \hfill \\ {\text{s}}.\;{\text{t}}.\;\frac{{{\sigma ^2}\theta }}{{1 + \theta }} \leqslant {\left( {g_k^{\left( {j,j} \right)}} \right)^{\text{H}}}g_k^{\left( {j,j} \right)} - \hfill \\ \frac{{\sum\limits_{l = 1}^K {p_l^{\left( j \right)}{{\left( {g_k^{\left( {j,j} \right)}} \right)}^{\text{H}}}g_l^{\left( {j,j} \right)}{{\left( {g_l^{\left( {j,j} \right)}} \right)}^H}g_k^{\left( {j,j} \right)}} }}{{{\sigma ^2} + {\text{tr}}\left( {\sum\limits_{l = 1}^K {p_l^{\left( j \right)}g_l^{\left( {j,j} \right)}{{\left( {g_l^{\left( {j,j} \right)}} \right)}^{\text{H}}}} } \right)}}, \hfill \\ \forall k \in \left\{ {1,2, \cdots ,K} \right\} \hfill \\ {p^{\left( j \right)}} \preccurlyeq {p^{\max \left( j \right)}}, \hfill \\ \end{gathered} $

(18)

2.2 下行阶段优化

在下行阶段，对于各个小区中的用户(1≤k≤K)下行传输速率的多目标优化问题，通过再次最小最大化(1≤j≤N)方式转化为单目标优化：

$ \begin{gathered} {\mathscr{P}_{{\text{DL1}}}}:\mathop {{\text{maximize}}}\limits_{{w^{\left( j \right)}},{t^{\left( j \right)}}} \mathop {\min }\limits_{1 \leqslant j \leqslant N} \left\{ {\mathop {\min }\limits_{1 \leqslant k \leqslant N} \left\{ {R_k^{{\text{DL}}\left( j \right)}} \right\}} \right\} \hfill \\ {\text{s}}.\;{\text{t}}.\;\;e_k^{\left( j \right)} \leqslant {\tau ^{{\text{UL}}}}p_k^{\left( i \right)},\forall j \in \left\{ {1,2, \cdots ,N} \right\}, \hfill \\ \forall k \in \left\{ {1,2, \cdots ,K} \right\} \hfill \\ \;\;\;\;{t^{\left( j \right)}} \in {T^{K \times 1}} \hfill \\ \;\;\;\;{\left\| {{w^{\left( j \right)}}} \right\|_2} = 1, \hfill \\ \end{gathered} $

(19)

其中：$R_{k}^{\text{DL}(j)}=t_{k}^{(j)}\cdot $

$ \begin{gathered} {\log _2}\left( {1 + \frac{{{q^{\left( j \right)}}{{\left| {{{\left( {g_k^{\left( {j,j} \right)}} \right)}^{\text{H}}}{w^{\left( i \right)}}} \right|}^2}}}{{\sum\limits_{i = 1,i \ne j}^N {{q^{\left( i \right)}}{{\left| {{{\left( {g_k^{\left( {i,j} \right)}} \right)}^{\text{H}}}{w^{\left( i \right)}}} \right|}^2}} + {\sigma ^2}}}} \right), \hfill \\ \;\;\;\;\;\;e_k^{\left( j \right)} = \left( {1 - t_k^{\left( j \right)}} \right)\eta _k^{\left( j \right)} \cdot \hfill \\ \sum\limits_{i = 1}^N {{{\left| {\sqrt {{q^{\left( i \right)}}} {{\left( {g_k^{\left( {i,j} \right)}} \right)}^{\text{H}}}{w^{\left( i \right)}}} \right|}^2}} 。\end{gathered} $

(20)

对于给定的$ t^{(j)}=\left[\begin{array}{llll}{t_{1}^{(j)}} & {t_{2}^{(j)}} & {\dots} & {t_{K}^{(j)}}\end{array}\right]^{\mathrm{T}}$，$ \mathscr{P}_{\text{ULI}}$可以转化为求解去除约束$ t^{(j)} \in T^{K \times 1}$后的$\mathscr{P}_{\mathrm{DL2} }\left(t^{(j)}\right) $，然后通过遍历$ t^{(j)} \in T^{K \times 1}$来找出使$\mathscr{P}_{\mathrm{DL2} }\left(t^{(j)}\right) $可解的t^(j)的取值。

定义(N·M)×1的增广矩阵$ \tilde{w}={{\left[ \begin{matrix} {{({{w}^{\left( 1 \right)}})}^{\text{T}}} & {{({{w}^{\left( 2 \right)}})}^{\text{T}}} & \ldots & \text{ }{{({{w}^{(N)}})}^{\text{T}}} \\ \end{matrix} \right]}^{\text{T}}}$，则有${{w}^{(j)}}={{E}^{(j)}}\tilde{w} $，其中E^(j)为从第(j－1)M+1列到jM列为M×M单位阵、其余元素全部为零的M×(N·M)的矩阵。

$ 定义:A_k^{\left( j \right)} = {q^{\left( j \right)}}{\left( {{E^{\left( j \right)}}} \right)^H}g_k^{\left( {j,j} \right)}{\left( {g_k^{\left( {j,j} \right)}} \right)^H}{E^{\left( j \right)}}, $

(21)

$ \begin{array}{l} B_k^{\left( j \right)} = \sum\limits_{i = 1,i \ne j}^N {{q^{\left( i \right)}}{{\left( {{E^{\left( i \right)}}} \right)}^H}g_k^{\left( {i,j} \right)}{{\left( {g_k^{\left( {i,j} \right)}} \right)}^H}{E^{\left( i \right)}}} + \\ {\sigma ^2}{\left( {{E^{\left( j \right)}}} \right)^H}{E^{\left( j \right)}}, \end{array} $

(22)

$ C_{k}^{(j)}=\eta_{k}^{(j)} \cdot \sum\limits_{i=1}^{N} q^{(i)}\left(E^{(i)}\right)^{H} g_{k}^{(i, j)}\left(g_{k}^{(i, j)}\right)^{H} E^{(i)}, $

(23)

$ {D^{(j)}} = {\left( {{E^{(i)}}} \right)^H}{E^{(i)}}。$

(24)

$ 因此:R_k^{{\rm{DL}}\left( j \right)} = t_k^{\left( j \right)} \cdot {\log _2}\left( {1 + \frac{{{{\tilde w}^H}A_k^{\left( j \right)}\tilde w}}{{{{\tilde w}^H}B_k^{\left( j \right)}\tilde w}}} \right), $

(25)

$ e_k^{(j)} = \left( {1 - t_k^{(j)}} \right){\tilde w^H}C_k^{(j)}\tilde w。$

(26)

因此$ \mathscr{P}_{\mathrm{DL} 2}\left(t^{(j)}\right)$可表述如下：

$ \begin{array}{l} {\mathscr{P}_{{\rm{DL}}2}}\left( {{t^{(j)}}} \right):\\ \mathop {{\rm{maximize}}}\limits_{\tilde w} \mathop {\min }\limits_{1 \le j \le N,1 \le k \le K} \left\{ {t_k^{\left( j \right)} \cdot {{\log }_2}\left( {1 + \frac{{{{\tilde w}^H}A_k^{\left( j \right)}\tilde w}}{{{{\tilde w}^H}B_k^{\left( j \right)}\tilde w}}} \right)} \right\}\\ {\rm{s}}.\;{\rm{t}}.\;\;{{\tilde w}^H}C_k^{\left( j \right)}\tilde w \ge \frac{{{\tau ^{{\rm{UL}}}}p_k^{\left( j \right)}}}{{1 - t_k^{\left( j \right)}}},\forall j \in \left\{ {1,2, \cdots ,N} \right\},\\ \forall k \in \left\{ {1,2, \cdots ,K} \right\}\\ {{\tilde w}^H}{\left( {{E^{\left( j \right)}}} \right)^H}{E^{\left( j \right)}}\tilde w = 1,\forall j \in \left\{ {1,2, \cdots ,N} \right\}。\end{array} $

(27)

引入中间变量θ：

$ \begin{array}{l} {\mathscr{P}_{{\rm{DL3}}}}\left( {{t^{\left( j \right)}}} \right):\mathop {\max {\rm{imize}}}\limits_{\tilde w,\theta } \theta \\ {\rm{s}}.\;{\rm{t}}.\;\;{{\tilde w}^H}A_k^{\left( j \right)}\tilde w \ge \left( {{2^{t_k^{\frac{\theta }{{\left( j \right)}}}}} - 1} \right){{\tilde w}^H}B_k^{\left( j \right)}\tilde w,\\ \forall j \in \left\{ {1,2, \cdots ,N} \right\},\forall k \in \left\{ {1,2, \cdots ,K} \right\}\\ {{\tilde w}^H}C_k^{\left( j \right)}\tilde w \ge \frac{{{\tau ^{{\rm{UL}}}}p_k^{\left( j \right)}}}{{1 - t_k^{\left( j \right)}}},\forall j \in \left\{ {1,2, \cdots ,N} \right\},\\ \forall k \in \left\{ {1,2, \cdots ,K} \right\}\\ {{\tilde w}^H}{D^{\left( j \right)}}\tilde w = 1,\forall j \in \left\{ {1,2, \cdots ,N} \right\}, \end{array} $

(28)

定义一个(N·M)×(N·M)的秩一的矩阵$ W=\tilde{w}{{{\tilde{w}}}^{H}}$，对于给定的θ和t^(j)，问题可转化为

$ \begin{gathered} {\mathscr{P}_{{\text{DL4}}}}\left( {\theta ,{t^{\left( j \right)}}} \right):{\text{Find}}\;W \hfill \\ {\text{s}}.\;{\text{t}}.\;\;tr\left( {\left( {{2^{t_k^{\frac{\theta }{{\left( j \right)}}}}} - 1} \right)B_k^{\left( j \right)}W} \right) \geqslant 0,\forall j \in \left\{ {1,2, \cdots ,N} \right\}, \hfill \\ \forall k \in \left\{ {1,2, \cdots ,K} \right\} \hfill \\ tr\left( {\left( {A_k^{\left( j \right)} - \left( {{2^{t_k^{\frac{\theta }{{\left( j \right)}}}}} - 1} \right)B_k^{\left( j \right)}} \right)W} \right) \geqslant 0, \hfill \\ \forall j \in \left\{ {1,2, \cdots ,N} \right\},\forall k \in \left\{ {1,2, \cdots ,K} \right\} \hfill \\ {\text{tr}}\left( {C_k^{\left( j \right)}W} \right) \geqslant \frac{{{\tau ^{{\text{UL}}}}p_k^{\left( j \right)}}}{{1 - t_k^{\left( j \right)}}},\forall j \in \left\{ {1,2, \cdots ,N} \right\}, \hfill \\ \forall k \in \left\{ {1,2, \cdots ,K} \right\} \hfill \\ {\text{tr}}\left( {{D^{\left( j \right)}}W} \right) = 1,\forall j \in \left\{ {1,2, \cdots ,N} \right\} \hfill \\ W \succcurlyeq 0 \hfill \\ {\text{rank}}\left( W \right) = 1。\end{gathered} $

(29)

此时若$ \mathscr{P}_{\mathrm{DL} 4}\left(\theta, t^{(j)}\right)$忽略约束rank(W)=1，则可通过半定松弛(Semidefinite Relaxation)^[21]方法来求解其最优解W^*。一般地，W^*为满秩矩阵，不满足约束rank(W)=1，我们通过求取W^*的近似秩一矩阵W₁^*作为$\mathscr{P}_{\mathrm{DL} 4}\left(\theta, t^{(j)}\right)$的近似解。令rank(W^*)=r，其特征值为λ₁≥λ₂≥…≥λ_r>0，对应的特征向量为u₁, u₂, …, u_r，则有$ W^{*}=\sum\limits_{i=1}^{r} \lambda_{i} u_{i}$，其中的一个近似秩一矩阵$W_{1}^{*}=\lambda_{1} u_{1} u_{1}^{H} $。由于前述问题中的系数矩阵A_k^(j)、B_k^(j)、C_k^(j)均为稀疏矩阵，导致W^*也为稀疏矩阵，并且满足：

$ {W^ * } = \left[ {\begin{array}{*{20}{c}} {{W^{\left( 1 \right) * }}}&0& \cdots &0\\ 0&{{W^{\left( 2 \right) * }}}& \cdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{W^{\left( N \right) * }}} \end{array}} \right], $

(30)

其中$ W^{(j) *}=E^{(j)} W^{*}\left(E^{(j)}\right)^{H}, j=1, 2, \cdots, N$。对于W^(j)*，其特征值为$\lambda _{1}^{(j)}\ge \lambda _{2}^{(j)}\ge \cdots \ge \lambda _{{{r}^{(j)}}}^{(j)}>0$，对应的特征向量为$ u_{1}^{(j)}, u_{2}^{(j)}, \cdots, u_{r^{(j)}}^{(j)}$，其中的一个近似秩一矩阵可表述为$ W_{1}^{(j) *}=\lambda_{1}^{(j) 1} u_{1}^{(j)}\left(u_{1}^{(j)}\right)^{H}$，因此cell-j中基站的波束成形向量近似解为$w^{(j) *}=\sqrt{\lambda_{1}^{(j)}}_{1} u_{1}^{(j)} $，也即$\mathscr{P}_{\mathrm{DL} 4}\left(\theta, t^{(j)}\right) $的近似解。

因此，我们首先对θ进行二分搜索，对于给定的θ通过遍历$t^{(j)} \in T^{K \times 1} $来尝试求解$\mathscr{P}_{\mathrm{DL} 4}\left(\theta, t^{(j)}\right) $，若可解，则求取使得$\mathscr{P}_{\mathrm{DL} 4}\left(\theta, t^{(j)}\right) $可解的最大值θ_DL^*，并且求取对应的近似解w^(j)*和遍历过程中使得$\mathscr{P}_{\mathrm{DL} 4}\left(\theta, t^{(j)}\right) $可解的t^(j)的取值t^(j)*。

3 仿真结果及分析

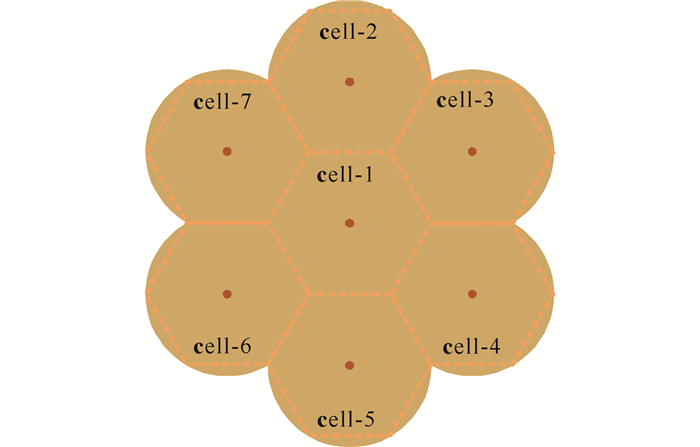
假设小区总数N=7，其几何分布方式如图 2所示，小区半径D=5 m，基站位于小区中心位置，各小区内用户数K=2，cell-i中的user-k到cell-j中基站的距离为d_k^{(i, j)}。假设用户以其所在小区的中心位置为极点的极坐标(d_k^{(j, j)}, α_k^(j))满足均匀分布：d_k^{(j, j)}~U(0, D)，α_k^(j)~U(0, 2π)。假设各小区基站的天线数M=3，基站下行发射功率q^(j)=－100 dBm，各用户能量捕获效率η_k^(j)=0.3，用户最大上行发射功率p_k^max(j)=－120 mdB，用户的信噪比(SNR)为20 dB。假设信道衰落模型为b_k^{(i, j)}=(10·d_k^{(i, j)})^－1.5，即信道系数满足g_mk^{(i, j)}~CN(0, (10·d_k^{(i, j)})^－1.5)，通过蒙特卡洛方法来模拟信道系数的分布概率。

假设下行单位时间T=1，根据文献[22]，取上行时间τ^UL=0.1。假设单位时间T可划分为10个时隙，故离下行时间分配矢量t^(j)的取值有9个，即

$ {t^{(j)}} \in {T^{K \times 1}} = \left\{ {\begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} {0.1}&{0.9} \end{array}} \right]}^{\rm{T}}}}&{{{[0.2\quad 0.8]}^{\rm{T}}}}&{{{\left[ {\begin{array}{*{20}{c}} {0.3}&{0.7} \end{array}} \right]}^{\rm{T}}}}& \cdots &{{{[0.9\quad 0.1]}^{\rm{T}}}} \end{array}} \right\} $

通过3组对比仿真实验进行分析，即上行阶段基站分别采取ZF、MRC、MMSE 3种方法进行检测，对于两种上下行传输的方式：其一是传统的上行阶段各用户以p^(j)=p^max(j)(即均为最大发射功率)进行传输、下行阶段基于p^(j)=p^max(j)各基站以$ {{t}^{(j)}}={{\left[ \begin{matrix} 0.5 & 0.5 \\ \end{matrix} \right]}^{\text{T}}}$ (即各用户平均分配时间)的下行传输，其二是本文所提出的上行阶段各用户以${{p}^{(j)}}=p{{_{\text{ZF}}^{(j)}}^{*}}, p{{_{\text{MRC}}^{(j)}}^{*}} $，或$ p{{_{\text{MMSE}}^{(j)}}^{*}}$ (即基于上行基站检测方式的最优功率)进行传输、下行阶段基于p^(j)=p^max(j)各基站以t^(j)=t^(j)*(即最优时间分配)进行下行传输，对比各自的最小传输速率，仿真实验结果如图 3所示。

根据上述3组仿真结果，可以得出本文所提出的上下行传输方式的最小传输速率与传统方式的比值(表 1)。其中，对于ZF检测而言，由于其最优功率分配为p_ZF^(j)*=p^max(j)，故实验所对比的两种上行传输方式实际上是相同的，从仿真结果上来看，图 2中各个数据在横坐标轴(最小上行传输速率)方向上是一致。对于MMSE检测而言，由公式(5)和(6)可知，MMSE与ZF比较类似，使得上行最优功率分配对上行传输速率的提高只有不到10%左右。而对于下行阶段而言，采取最优时间分配方式进行传输可以将最小传输速率提高60%以上。

4 结论

本文在WPCN中的“捕获-传输”协议基础上，提出一种新的在蜂窝小区中进行能量与信息联合传输的设计方案，将无线信息与能量的同时传输(SWIPT)应用于WPCN的下行传输，实现基站与用户之间的下行能量传输与上下行双向信息传输。通过非线性规划来进行问题描述与优化求解，将整个问题串行地分为上、下行两个子问题。上行阶段通过优化特定的目标函数来求解各小区内各用户的上行发送功率，并作为参数输入到下行阶段的问题求解。下行阶段则通过优化特定的目标函数：对于各小区内的基站，求解其波束成形矢量；对于各个用户分组，求解其能量捕获与信息解码的时间分配矢量。仿真结果表明，与传统的传输方式相比，本方案显著提高用户的最小传输速率。