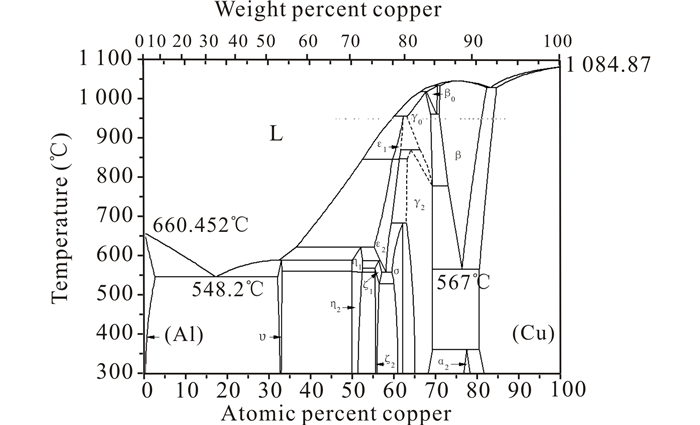
【研究意义】 Cu作为铝合金中常见的合金元素，对铝合金的强度，耐热性以及加工性能起到了良好的强化作用，在航空航天结构件、微电子、焊接、机械加工、粉末冶金等领域有着广泛的应用^[1-4]。由于Al和Cu在性能方面差别显著，并且Al-Cu接头的焊接问题是Al-Cu双金属复合结构实用化的关键^[5]。因此研究二者之间的扩散行为具有十分重要的意义。【前人研究进展】由Al-Cu二元相图(图 1)^[6-7]可知，不同的实验方法和处理条件，得到的中间化合物的数量有所不同。目前有人通过制作Al-Cu薄膜的方法，观察到了一种金属间化合物^[8]，通过扩散焊方法观察到3层不同的组织^[9]，利用扩散偶的方法得到了4种金属间化合物^[10]，以及采用“铆钉法”观察到了6种化合物^[11]。【本研究切入点】截至目前，很少有人对中间化合物的生长行为和扩散系数的计算进行研究。【拟解决的关键问题】本文通过扩散偶的方法，在540℃的退火温度下，观察到了全部的4种IMCs，并对该温度下中间相的生长以及互扩散系数的计算进行了更为详尽的实验和理论分析，为以后进一步的研究提供参考依据。

图 1 (Fig. 1)

图 1 Al-Cu二元相图 Fig.1 The Al-Cu phase diagram[6-7]

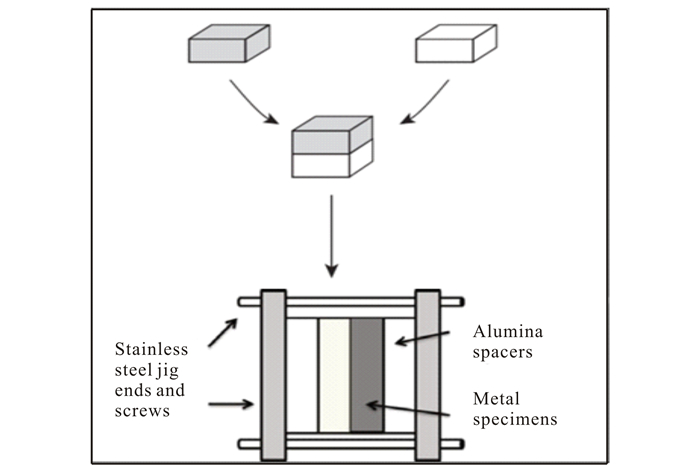
实验中选用Al柱(99.99 wt%)和Cu块(99.99 wt%)作为原始材料。将金属切成5 mm×5 mm×5 mm的立方体。将这些立方体镶嵌后，在酒精中用240~3 000目的砂纸从粗至细依次进行打磨，最后用钻石膏抛光，以此来获得高质量的表面。将磨好的样品超声清洗2~3次，干燥后，用不锈钢夹具将Al块和Cu块捆扎在一起，为了防止金属块与夹具之间的反应以及增大两个金属块之间的受力面积，在Al-Cu扩散偶的上、下表面加一层钽片，最后用螺丝紧固(图 2)。将扩散偶样品密封在真空石英玻璃管中，在540℃的管式炉中分别退火36 h、48 h和60 h。温度误差控制在±2℃的范围内。为保持样品的高温微观结构和局部化学组成，对样品进行淬火处理，最后再镶嵌、抛光。

图 2 (Fig. 2)

图 2 扩散偶的制备示意图 Fig.2 The schematic diagram of diffusion couple

首先在光学显微镜下观察扩散偶是否形成扩散层，然后使用具有波长色散谱(WDS)的JEOL 8230电子探针显微分析仪(EPMA)来获得扩散区中相层的组成分布，来测定每个扩散偶样品中Al和Cu的浓度分布。EPMA加速电压为15 kV，电子束电流是20 nA。

图 3展示了Al-Cu扩散偶样品在540℃下退火48 h的背散射图像，图 4是由EPMA测定的浓度距离曲线。根据Al-Cu二元相图，在540℃的温度下存在4个IMCs，即θ、η₂、ζ₂和γ₁。本实验中，我们可以在所有扩散偶中观察到4种化合物，并且经过EPMA测定，可确定4个金属间化合物分别为Al₂Cu、Al_0.939Cu_0.987、Al₉Cu_11.5和Al₄Cu₉。在背散射图上可以看出，Al-Cu扩散偶在界面处形成了厚度均匀的的扩散层，厚度大约为160 μm，并且扩散层内包含4个衬度不同的亚层，代表 4个中间相。目前的结果与Al-Cu二元相图相吻合。

图 3 (Fig. 3)

图 3 Al-Cu扩散偶在540℃退火48 h的背散射电子图 Fig.3 The BSE image of the interdiffusion zone in the Al-Cu couple annealed at 540℃ for 48 h

图 4 (Fig. 4)

图 4 Al-Cu扩散偶在540℃退火48 h的成分曲线 Fig.4 Concentration profiles of Al-Cu couple annealed at 540℃ for 48 h

在扩散过程中，扩散层的厚度主要受到生长动力学的影响，在相层生长的过程中可以根据层厚来确定相关的动力学参数。一般来说，扩散偶样品中，扩散层的厚度与时间可以通过下面的关系式来表示：

式中，l是扩散层厚度，t是退火时间，k_p是生长常数，n是一个变量，它的取值取决于扩散机制，若为体积扩散控制的生长，n取0.5，若为界面扩散控制的生长，则n取1。

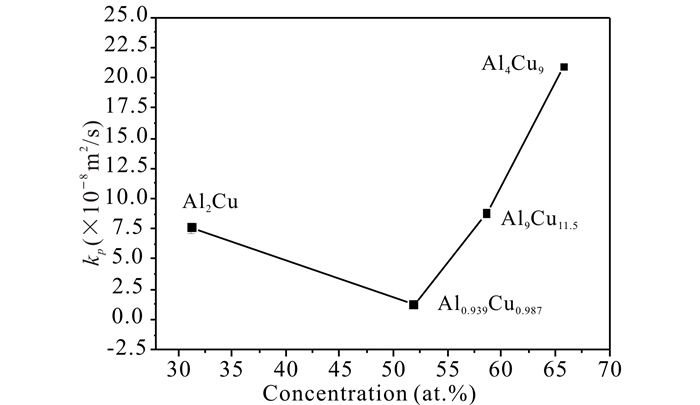
在扩散过程中，初始阶段的生长主要由界面扩散控制，而扩散到一定的厚度时，体积扩散将起主导作用。本实验中，为了验证在540℃下扩散层的生长机制，我们做了该温度下扩散层的厚度和时间平方根的关系图(图 5)，图 6为金属间化合物的生长常数随Cu浓度的变化趋势。该退火温度下不同时间的扩散层的厚度见表 1。显然，扩散层厚度l和退火时间的平方根呈现出很好的线性关系，这也就表明金属间化合物的生长是受体扩散控制的，而体扩散主要为空位扩散机制。

图 5 (Fig. 5)

图 5 540℃扩散层厚度和退火时间平方根之间的关系 Fig.5 Layer thickness vs square root of diffusion anneal time at 540℃

图 6 (Fig. 6)

图 6 540℃金属间化合物的生长常数随Cu浓度的变化趋势 Fig.6 The growth constant of intermetallic compounds varies with the concentration of Cu at 540℃

表 1(Table 1)

表 1 不同退火时间下金属间化合物的厚度(×10-6 m) Table 1 Thickness of intermetallic compounds at different annealing times (×10-6 m) Phase Al2Cu Al0.939Cu0.987 Al9Cu11.5 Al4Cu9 Total 36 h 30.7 3.6 34.2 82.1 150.6 48 h 31.8 5.5 36.4 86.4 160.1 60 h 32.3 5.9 38.4 92.7 169.3
	表 1 不同退火时间下金属间化合物的厚度(×10-6 m) Table 1 Thickness of intermetallic compounds at different annealing times (×10-6 m)

Al-Cu体系中间化合物和扩散层总厚度的生长常数在表 2中给出。通过表 2我们可以看出，随着温度的升高，每个相的生长常数都在升高，表明温度是影响中间化合物生长的主要因素之一。由于Al₄Cu₉相的厚度和生长常数比其他3个相的总和还要大，因此，Al₄Cu₉相阶段的生长主要控制金属间层的生长。

表 2(Table 2)

表 2 金属间化合物的生长常数和扩散系数 Table 2 Growth constants and diffusion coefficients of intermetallic compounds Phase Al2Cu Al0.939Cu0.987 Al9Cu11.5 Al4Cu9 Total kp(m2/s) (7.58±0.443)×10-8 (1.22±0.009)×10-8 (8.74±0.346)×10-8 (2.09±0.080)×10-7 (3.85±0.151)×10-7 Dint(m2/s) 3.14×10-13 1.09×10-13 6.91×10-13 1.48×10-12 ——
	表 2 金属间化合物的生长常数和扩散系数 Table 2 Growth constants and diffusion coefficients of intermetallic compounds

为了更好地了解相互扩散过程，对扩散系数的计算是十分必要的。因为所有中间相的生长都是在很窄的范围内进行的，且每个相的厚度都不是均匀不变的，不可能准确的测量出很小浓度的扩散系数。因此，Wagner^[12]提出了一种用整体扩散系数来表征均匀性范围内的互扩散系数的方法，如下所示：

其中，其中N_i是关于组分i的平均组成，${{N}_{i}}=N_{i}^{''}-N_{i}^{'}$是相关产物相的未知均匀性范围。因此，${{\widetilde{\mathit{D}}}_{\text{int}}}$能够从轮廓图中估算出来。

对于生成金属间化合物的化学扩散，浓度梯度会很小，对于这种情况可以对式(2)进行优化，以此来计算平均扩散系数。计算方法的表达式为^[13]

式中$V_{m}^{v}$是第v相的摩尔体积，在计算中我们认为它是一个常数，它的数值可以由晶格常数计算得到。$N_{i}^{+}、N_{i}^{-}、N_{i}^{\beta }$分别是β相最右侧、最左侧和平均的浓度，Δx_β是β相的宽度，t是退火时间。

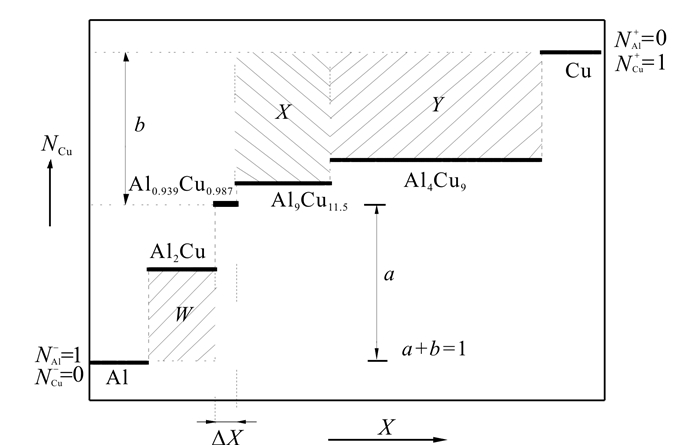
图 7为扩散系数的计算示意图，公式(4)为以η₂相为例的互扩散系数的表达式。通过这个方法，我们可以比较准确地估算每个金属间化合物的平均有效互扩散系数(表 2)。

图 7 (Fig. 7)

图 7 中间相扩散系数的计算示意图 Fig.7 Schematic diagram of calculation of mesophase diffusion coefficient

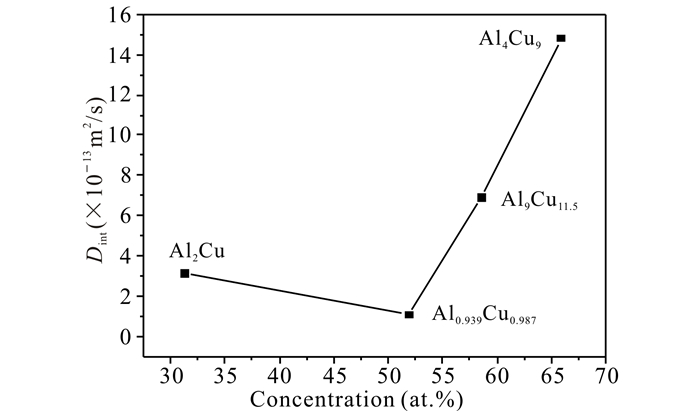
可以看出，扩散系数随温度的升高而增大，并且在温度相同的条件下Al₄Cu₉相的扩散系数最大，Al_0.939Cu_0.987相的扩散系数最小，两相的互扩散系数相差一个数量级左右。4种金属间化合物的扩散系数随Cu浓度的变化趋势如图 8所示。

图 8 (Fig. 8)

图 8 540℃金属间化合物的扩散系数随Cu浓度的变化趋势 Fig.8 Variation trend of intermetallic compound diffusion coefficient with the concentration of Cu at 540℃

本文用扩散偶的方法对Al-Cu二元体系在540℃时的扩散行为进行研究。在所有样品中都可以观察到4种金属间化合物θ(Al₂Cu)、η₂(Al_0.939Cu_0.987)、ζ₂(Al₉Cu_11.5)和γ₁(Al₄Cu₉)。金属间化合物的生长符合抛物线生长规律，并且我们估算了各相的抛物线生长常数。金属间化合物的生长主要受到体扩散的控制。对中间相的扩散系数的计算方法进行了详细的介绍。研究表明，Al₄Cu₉的生长常数和扩散系数都是4个中间化合物中最大的，而且随着温度的升高，生长常数和扩散系数也在增加。