【研究意义】钦州湾位于广西壮族自治区南部钦州市以南,由内湾(茅尾海)和外湾(狭义的钦州湾)组成,湾内岛屿众多,岸线曲折,具备建设大型港口的自然资源条件。根据钦州港总体规划及临港工业区发展规划,钦州港的港口定位是地区性重要港口,远期将发展成为工业服务为主的多功能现代化国际贸易深水港,到2020年,钦州港港口功能区需填海造地58.3 km2。因此,研究钦州湾围填海工程引起的泥沙扩散情况对海洋环境保护有重要意义。【前人研究进展】李树华等[1-2],陈波等[3-4],鲍献文等[5],宋德海等[6],游慕贤等[7]和孙永根等[8]通过观测数据和数值模型对钦州湾的水动力特征进行了研究,但有关钦州湾泥沙扩散的研究不多。王玉海等[9-10]通过历史观测数据和FVCOM模型研究了围填海工程对钦州湾水下地形冲淤演变的影响,提出大量工程的叠加效应不能忽略。董德信等[11]利用Mike模型模拟了2008年和2012年钦州湾岸线变化对悬浮泥沙扩散和底质冲淤变化的影响。孙永根等[12]通过2007年和2010年的实测泥沙数据分析了钦州湾的泥沙分布特征,提出悬浮泥沙主要受潮流控制。【本研究切入点】随着钦州湾大量围填海工程的实施,有必要构建一个蓄泥坑来储泥,为下一个工程提供原料,但这种海上工程产生的泥沙扩散对周围环境会产生怎样的影响还没有文献进行描述。【拟解决的关键问题】基于ECOMSED模型,本研究详细分析蓄泥坑引起的水动力变化和泥沙扩散特征,并进行多种围挡施工的情景模拟,试图找出对环境影响最小的施工方法。
1 模型的建立 1.1 模型采用的ECOMSED模型,共包含6个模块:水动力模块、黏性和非黏性泥沙输运模块、沉积物示踪模块、可溶性粒子输运模块、热通量模块和风浪模块,该模型在模拟浅海污染物和泥沙输运方面有独特的优势。该模型采用了基于静力学假设和Boussinesq近似下的海洋封闭方程组;在水平方向上采用曲线正交网格,即Arakawa C网格;在垂直方向上采用sigma坐标,在拟合底地形方面比z坐标更准确,同时垂向上嵌套了2.5阶湍封闭模型。模型的计算通过内外模的分离,提高了计算速度,在计算时其水平项和时间变化上采用显式差分,垂向上采用隐式差分。
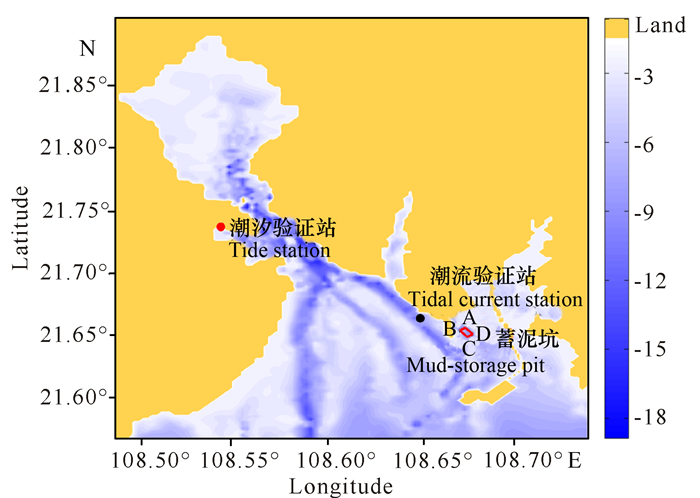
模型计算区域位于108.48°~108.84°E,21.5675°~21.9°N(图 1)。水平方向网格数为134×105,水平分辨率为0.15′,约为258 m。由于钦州湾的水深较浅,因此垂向上仅分成7个sigma层。开边界采用辐射边界条件,以潮汐调和常数驱动。本研究采用K1,O1,P1,M2,S2和N2等6个分潮,调和常数来自俄勒冈大学的中国海潮汐模型(http://volkov.oce.orst.edu/tides/YS.html),该模型在中国海的水平分辨率为1/30°,其中K1和M2的均方根误差(RMS)分别为1.63 cm和4.16 cm[13]。水深场采用海图水深,由于海图水深基准面为最低低潮面,因此需要将数据转化成平均海平面下的水深。
|
红色和黑色圆圈分别代表潮位和潮流验证点 Red circle:Water level station; Black circle:Tidal current station 图 1 钦州湾水深分布 Fig.1 The bathymetry in Qinzhou Bay |
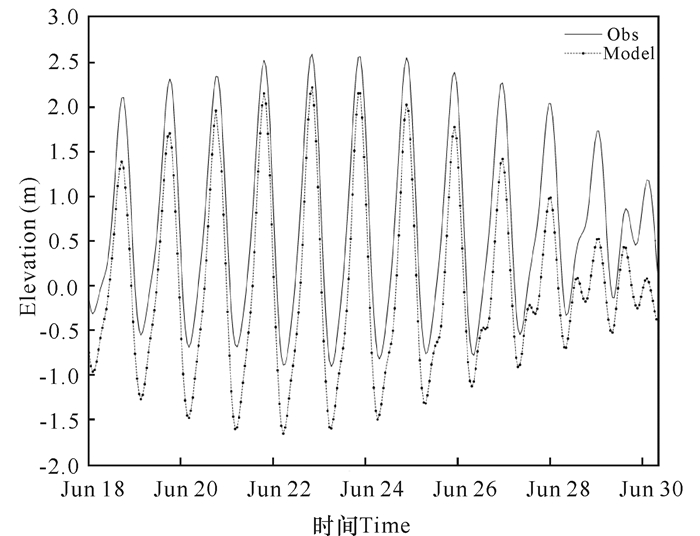
图 1为钦州湾水深分布图,其中潮位验证点位于龙门(图 1中的红色圆圈),经纬度为108.54°E,21.73°N。图 2为观测和模型的潮位对比结果,观测时间为2009年1月18日至1月30日。可以看出观测潮位值与模型结果位相一致,变化同步,基本吻合。众所周知,实测的潮位值不仅包括周期性的变化,还包括一些扰动,因此模型与观测值的偏差在所难免,只要在一定幅度内都是可以接受的。
|
实线:实测值; 点划线:模拟值 Solid line:Observation value; Dash line:Simulated value 图 2 龙门站实测和模拟潮位比较 Fig.2 Comparison of observed and modeled water level at Longmen station |
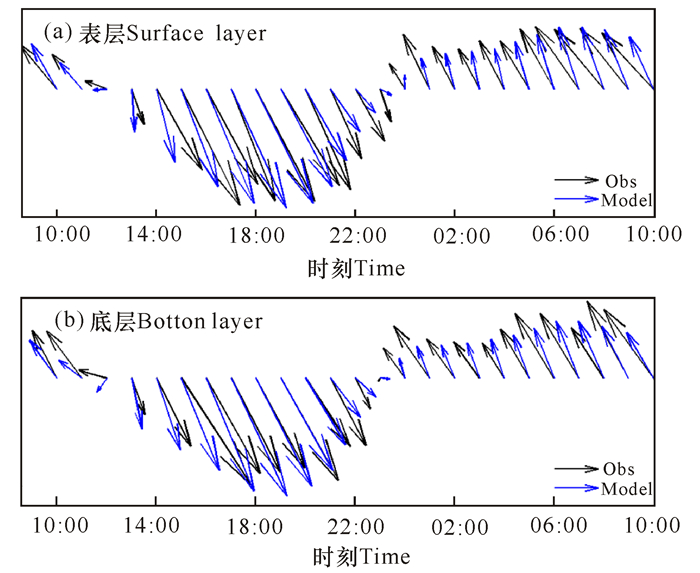
选取钦州湾东南部离岸较远的海流观测点来验证模型的准确性,站点位置如图 1中的黑色圆圈所示,经纬度为108.6481°E,21.6625°N,海流观测时间为2009年11月10日的上午10:00至11月11日的上午10:00。观测表明,钦州湾的表层平均落潮流速为0.6 m/s,平均涨潮流速为0.36 m/s,落潮时间为11 h,涨潮时间为14 h。底层的转向流时刻、涨潮时间、落潮时间与表层基本一致。受底摩擦力影响,底层的流速值小于表层流速,底层的平均落潮流和涨潮流的流速分别为0.46 m/s和0.29 m/s。从图 3可以看出观测值与模型值基本吻合,但模型值比观测值略小,这与本研究只采用潮汐驱动未考虑季风等强迫因子有关。同时观测值和模型结果都显示钦州湾呈典型的全日潮流特征,落潮流流速略大于涨潮流流速。
|
黑色线:实测值; 蓝色线:模型值 Black:Observation value; Blue:Simulated value 图 3 钦州湾表层和底层海流观测值和模型值验证结果 Fig.3 Comparison of simulated and observed tidal current in the surface and bottom layer in Qinzhou Bay, respectively |
由于钦州湾的浅滩较多,所以在ECOMSED模型中加入干/湿网格判据,其中水动力模型的具体设置如下:
设置最小水深ε=0.1 m,当(Di-1,j+Di,j)*0.5≤ε时水点干出,若(Di-1,j+Di,j)*0.5>ε时参与计算,其中D=H+η,H为相对于平均海平面的水深,η代表水位。
若(Di-1,j+Di,j)*0.5>ε,当Di-1,j>0且Di,j>0时,ui,j用动量方程计算,其它情况设为0;当Di,j-1>0且Di,j>0时,vi,j用动量方程计算,其它情况设为0。
1.3 泥沙输运模型设置ECOMSED可以模拟粘性和非粘性泥沙的输移,粘性泥沙由粘土、粉砂和有机物质组成,其再悬浮、沉积和输运用SED模块模拟。非粘性泥沙主要是细砂,使用van Rijn程序[14]计算。底床屏蔽的影响也引入了非粘性泥沙的输运模拟。这里床砂质的输移没有被考虑,因为它不会明显影响水体的光学性质。泥沙输移模块可以预测下列时空分布:(1)粘性与非粘性沙的悬沙浓度;(2)沙床高程的变化;(3)沙-水界面通量;(4)沙床组成的变化。具体控制方程如下:
其中泥沙的控制方程为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\frac{{\partial {C_k}}}{{\partial t}}{\rm{ }} + \frac{{\partial U{C_k}}}{{\partial x}} + \frac{{\partial V{C_k}}}{{\partial y}} + \frac{{\partial (W - {W_{s, k}}){C_k}}}{{\partial z}} = \\ \frac{\partial }{{\partial x}}({A_H}\frac{{\partial {C_k}}}{{\partial x}}) + \frac{\partial }{{\partial y}}({A_H}\frac{{\partial {C_k}}}{{\partial y}}) + \frac{\partial }{{\partial z}}({K_H}\frac{{\partial {C_k}}}{{\partial z}}) + S{\rm{。}} \end{array} $ | (1) |
自由表面边界条件:
| $ {K_H}\frac{{\partial {C_k}}}{{\partial z}} = 0, z \to \eta {\rm{。}} $ | (2) |
底边界条件:
| $ {K_H}\frac{{\partial {C_k}}}{{\partial z}} = {E_k} - {D_k}, z \to - H{\rm{。}} $ | (3) |
侧边界条件:
| $ \frac{{\partial {C_k}}}{{\partial n}} = 0, $ | (4) |
其中U, V, W分别为x向,y向及z向的流速,Ws,k为泥沙的沉降速度,Ck为悬浮的粘性或非粘性泥沙的浓度,AH为水平扩散系数,KH为湍扩散系数,Ek和Dk分别为再悬浮通量和沉降通量,η为水位高度,H为水深,S为泥沙源强。
泥沙再悬浮通量表达式为
| $ {E_q} = \frac{{(s{q_s} - qz{C_z})\Delta t}}{{\Delta x\Delta y}}, $ | (5) |
其中Cz为海底层的悬浮泥沙浓度,而qs的计算公式为
| $ {q_s} = Fzu{C_a}{\rm{。}} $ | (6) |
另外,泥沙沉降通量的表达式为
| $ {D_2} = {W_{s, 2}}{C_2}, $ | (7) |
其中D2为非粘性泥沙的沉降通量,而Ws,2为沉降速度,C2为海底的悬浮泥沙浓度。
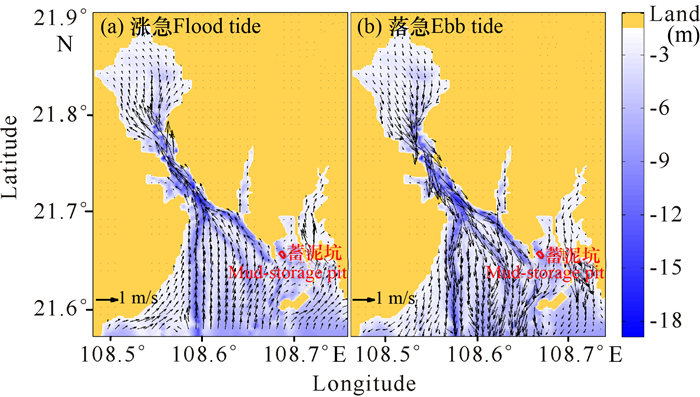
2 结果与分析 2.1 钦州湾流场分布从图 4可以发现钦州湾潮流运动形式以往复流为主,涨潮中间时大部分海域流向以偏北方向为主,涨潮流从湾口汇入龙门峡口,至茅尾海后呈放射状散开,流向总体较均匀,局部受地形影响而发生偏转。开阔水域流速较大,流向较均匀,浅滩、岛屿周围以及岸边流速相对较小,流向多变;航道和深槽处流速最大,流向与航道、深槽走向基本一致。最大潮流流速为1.85 m/s,对应流向347°,平均流速0.34 m/s,平均流向为148°。落潮中间时钦州湾大部分海域的潮流为偏南向,落潮流从茅尾海汇入龙门峡口,至钦州外湾后呈放射状散开。最大潮流流速为2.34 m/s,对应流向160°,平均流速为0.46 m/s,平均流向为176°。落潮流大于涨潮流。涨潮时,保税港区航道附近涨落潮潮流分为两支,一支顺着公路流向廘耳环江附近海域,另一支绕过保税港区顺着航道至金鼓江口,再分两支,一支流入金鼓江,溯江而上;另一支则继续沿着航道过龙门进入茅尾海;落潮时过程则反之,水流沿水道、航道以及公路两侧流向钦州外湾,潮流呈现典型往复流特征。无论是涨落潮,航道附近的流速均较其它区域大。
|
(a)涨潮中间时; (b)落潮中间时 (a)In the middle of flood tide; (b)In the middle of ebb tide 图 4 钦州湾大潮期流场分布 Fig.4 The distribution of tidal current during spring tide in Qinzhou Bay |
蓄泥坑长度为710 m,宽度为400 m,面积约为28.41万m2(位置如图 1红色标记所示),对应的4点位置分别为A(108.6729°E,21.6549°N)、B(108.6699°E,21.6527°N)、C(108.6739°E,21.6476°N)、D(108.6770°E,21.6498°N)。为此,需要分析蓄泥坑对周围流场的影响,由于钦州湾落潮流大于涨潮流,因此本研究选取落潮中间时刻来分析蓄泥坑工程前后的流场变化。从图 5可以发现蓄泥坑的北部基本为西南向流,东部基本为南向流,南部和西部为东南向流。
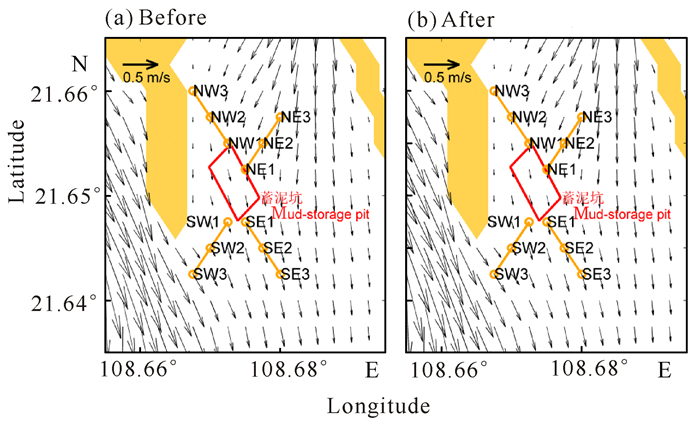
|
图 5 表层落潮中间时蓄泥坑工程前后流场分布特征 Fig.5 The distribution characteristics of surface current before and after construction of mud-storage pit in the middle of ebb tide |
为了详细分析工程前后的流场变化,本研究在4个角分别选取3个站点来分析流速和流向变化(图 5),结果如表 1所示。表层落潮中间时,工程前后流速偏差最大的两个站为NE1和NW1站,其流速偏差分别达到2.68 cm/s和1.65 cm/s,而且这两个站工程前后的流向偏差分别为5.20°和7.91°,同时NE2站的流向偏差也达到了6.89°。总的来讲,蓄泥坑东北部的流速和流向影响最大,平均流速偏差为1.40 cm/s,平均流向偏差为5.05°。表层涨潮中间时(未展示),蓄泥坑西北部的NW1站和NW2站影响较大,流速偏差和流向偏差分别为(0.6 cm/s,7.34°)和(0.35 cm/s,3.71°)。
| 表 1 表层落潮中间时蓄泥坑工程前后流速流向变化 Table 1 The variation of surface current speed and direction before and after construction of mud-storage pit in the middle of ebb tide |
底层的流场分布与表层基本相似,蓄泥坑的北部为西南向流,东部为南向流,而南部和西部为东南向流。与表层落潮中间时一样,底层落潮中间时(图 6)工程前后蓄泥坑东北部的流速流向偏差最大,平均流速偏差为0.53 cm/s,平均流向偏差为4.55°(表 2)。表层与底层变化基本相同,蓄泥坑东北部的流速偏差都为10%左右。但与表层相比,底层的NW1站流速变化更大,其底层流速偏差为24%,而表层流速偏差仅为16.2%。
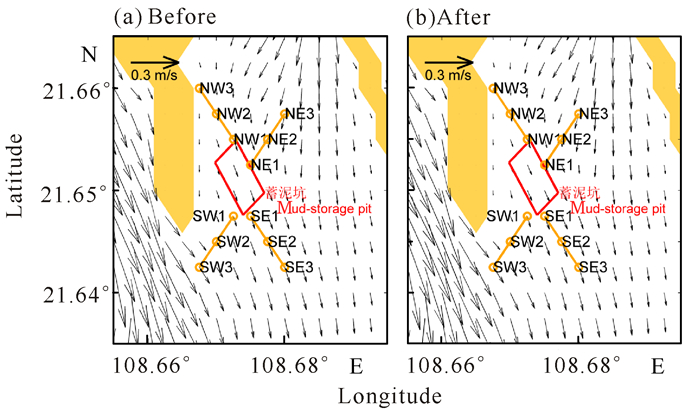
|
图 6 底层落潮中间时刻蓄泥坑工程前后流场分布特征 Fig.6 The distritution characteristics of bottom current before and after construction of mud-storage pit in the middle of ebb tide |
| 表 2 底层落潮中间时蓄泥坑工程前后断面流速流向变化 Table 2 The variation of bottom current speed and direction before and after construction of mud-storage pit in the middle of ebb tide |
本研究在水动力模型基础上,嵌套泥沙输运模型模拟蓄泥坑挖泥期泥沙对周围环境的影响,由于主要模拟蓄泥坑挖泥期产生的悬浮泥沙对周围环境的影响,因此背景泥沙浓度设为0,开边界泥沙浓度也设为0。
另外,蓄泥坑采用规格为4 500 m3/h的耙吸式挖泥船挖泥,而耙吸式挖泥船挖泥过程搅动水体产生的悬浮泥沙量与挖泥船类型与大小、耙头种类、水力吸入能力的大小、作业现场的波浪与水流、现场水盐度、底质粒径分布有关。为减小溢流悬浮泥沙源强,在满仓溢流处设置过滤沉淀槽,槽壁内外加过滤网,进入槽内含泥沙水体沉淀后进入内侧二次沉淀槽,沉淀后通过溢流管排放,溢流管排放口设置在海底面上0.5 m处。通过二次沉淀过滤,溢流水体含泥量约为10~15 kg/m3,按含泥量最大15 kg/m3,计算当采用4 500 m3/h耙吸式挖泥船作业时,满舱溢流泥沙量(Q值)最大为18.75 kg/s。
根据2014年12月《钦州港30万吨级进港航道支航道工程疏浚物倾倒吹填拟设蓄泥坑周边海域海洋环境质量评估报告》,该区域砂(2~0.063 mm)和粉砂(0.063~0.004 mm)的比例约为62%和32%,因此本研究的泥沙中值粒径设为1.1 mm。另外,计算泥沙沉速的公式较多(张瑞瑾[15],钱宁和万兆惠[16]),且多数实验在理想状态下,而实际海洋中泥沙沉降受海流扰动,泥沙颗粒互相干扰等因素影响,因此本研究取保守值0.5 mm/s。模拟一个月后,泥沙扩散基本趋于稳定,取垂向平均结果来进行分析(图 7)。浓度为10 mg/L、50 mg/L、100 mg/L的悬浮泥沙扩散面积分别为70.88 km2、36.64 km2及22.93 km2,影响范围较大。其中10 mg/L的包络线向西和向南最远端扩散了6.67 km和6.2 km,已影响到保留区和航道,而东边由于三墩公路的阻挡不会影响旅游保护区。
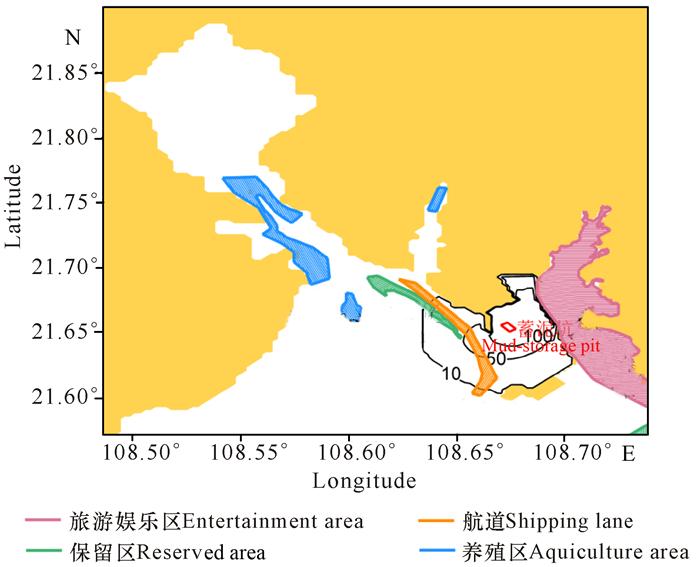
|
图 7 蓄泥坑挖泥引起的泥沙扩散分布 Fig.7 The diffusion distribution of SS during the construction of mud-storage pit |
为此,本研究进行了4个围挡模拟实验(图 8)。在东开口和西开口实验中,泥沙扩散面积与无围挡实验基本相同;而南开口和北开口实验中,泥沙扩散面积明显减小(表 3)。南开口实验中(图 8b),溢流口选在西南角,浓度为10 mg/L悬浮泥沙的面积仅为无围挡实验的70.9%,而50 mg/L和100 mg/L悬浮泥沙的面积仅为无围挡实验的76.2%和78.2%。北开口实验中,泥沙扩散的影响面积最小,其泥沙包络线明显小于无围挡实验(图 8d)。其中10 mg/L、50 mg/L、100 mg/L悬浮泥沙的扩散面积分别为31.01 km2、15.12 km2及12.52 km2,只为无围挡实验的42.3%,41.3%以及54.6%。10 mg/L悬浮泥沙的包络线向西和向南最远端扩散了4.7 km和4.4 km,只对航道和保留区的南端有所影响。
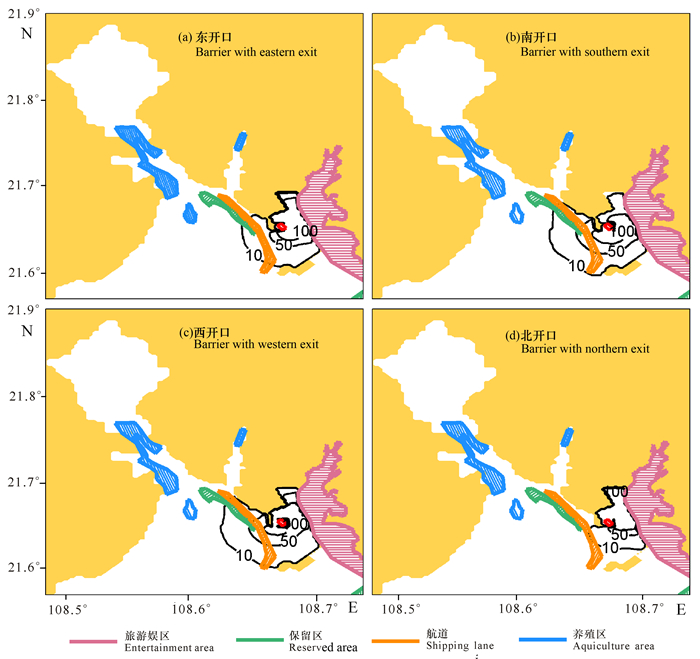
|
图 8 4个敏感性实验的泥沙扩散分布 Fig.8 The distribution of SS in the four sensitivity experiments |
| 表 3 蓄泥坑挖泥围挡实验结果分析 Table 3 Analysis of experimental results on mud-storage pit |
本研究基于三维ECOMSED模型分析了钦州湾背景流场,并基于水动力场模拟了蓄泥坑开挖期间的泥沙扩散特征,并进一步通过敏感性实验测试了不同围挡实验对减少泥沙扩散面积的效果。结果发现:
钦州湾潮流场呈往复流特征,涨潮中间时大部分海域流向以偏北方向为主,最大潮流流速为1.85 m/s,对应流向347°,平均流速0.34 m/s,平均流向为148°。落潮中间时钦州湾大部分海域的潮流为偏南向,最大潮流流速为2.34 m/s,对应流向160°,平均流速为0.46 m/s,平均流向为176°。落潮流大于涨潮流。无论是涨落潮,航道附近的流速均较其他区域大。
落潮中间时蓄泥坑的北部基本为西南向流,东部基本为南向流,南部和西部为东南向流。无论表层还是底层,蓄泥坑东北部的流场在工程前后变化较大,流速偏差约为10%。表层和底层的平均流向偏差分别为5.05°和4.55°。
无围挡实验中,10 mg/L、50 mg/L、100 mg/L悬浮泥沙的扩散面积分别为70.88 km2、36.64 km2及22.93 km2,影响范围较大。其中10 mg/L悬浮泥沙的包络线已影响到保留区和航道。围挡实验中,东开口和西开口泥沙扩散面积与无围挡实验基本相同。而南开口和北开口泥沙扩散面积明显减小,尤其北开口实验中10 mg/mL的悬浮泥沙包络线面积仅为无围挡实验的42.3%, 因此采用三面围挡仅北端开口的施工可以显著降低泥沙扩散对周围海洋环境的影响。
| [1] |
李树华, 童万平. 钦州湾潮流和污染物扩散的数值模型(Ⅰ)钦州湾潮流的数值模拟[J]. 海洋环境科学, 1987, 6(2): 30-37. LI S H, TONG W P. Numerical model of tidal current and pollutant diffusion in the Qinzhou Bay:Numerical modeling of tidal current in the Qinzhou Bay[J]. Marine Environment Science, 1987, 6(2): 30-37. |
| [2] |
李树华, 夏华永, 梁少红, 等. 广西重点港湾的潮流和余流[J]. 广西科学, 2001, 8(1): 74-79. LI S H, XIA H Y, LIANG S H, et al. Tidal currents and residual currents in the key harbors of Guangxi[J]. Guangxi Sciences, 2001, 8(1): 74-79. |
| [3] |
陈波, 邱绍芳, 葛文标, 等. 广西沿岸主要海湾潮流的数值计算[J]. 广西科学, 2001, 8(4): 295-300. CHEN B, QIU S F, GE W B, et al. Numerical calculation about the tidal currents in the main bays of Guangxi[J]. Guangxi Sciences, 2001, 8(4): 295-300. |
| [4] |
陈波, 侍茂崇, 邱绍芳. 广西主要港湾余流特征及其对物质输运的影响[J]. 海洋湖沼通报, 2003(1): 13-21. CHEN B, SHI M C, QIU S F. Characteristics of residual currents and their influence on the material transformation in five main bays of Guangxi coast[J]. Transactions of Oceanology and Limnology, 2003(1): 13-21. |
| [5] |
鲍献文, 陈波, 侍茂崇, 等. 钦州湾三维潮流数值模拟[J]. 广西科学, 2004, 11(4): 375-378, 384. BAO X W, CHEN B, SHI M C, et al. The numerical value simulation of the three dimensional tide of the Qinzhou Bay[J]. Guangxi Sciences, 2004, 11(4): 375-378, 384. |
| [6] |
宋德海, 鲍献文, 朱学明. 基于FVCOM的钦州湾三维潮流数值模拟[J]. 热带海洋学报, 2009, 28(2): 7-14. SONG D H, BAO X W, ZHU X M. Three-dimensional numerical simulation of tidal current in the Qinzhou Bay[J]. Journal of Tropical Oceanography, 2009, 28(2): 7-14. |
| [7] |
游慕贤, 游立新. 钦州湾围滩工程前后潮流场的数值模拟[J]. 水道港口, 2009, 30(6): 394-401. YOU M X, YOU L X. Numerical simulation of tidal current field before and after engineering project in Qinzhou Bay[J]. Journal of Waterway and Harbor, 2009, 30(6): 394-401. |
| [8] |
孙永根, 高俊国, 朱晓明. 钦州保税港区填海造地工程对海洋环境的影响[J]. 海洋科学, 2012, 36(12): 84-89. SUN Y G, GAO J G, ZHU X M. Effect of reclamation engineering in Qinzhou Bond Harbor on marine environment of Qinzhou Bay[J]. Marine Sciences, 2012, 36(12): 84-89. |
| [9] |
王玉海, 王崇浩, 刘大滨, 等. 钦州湾水道稳定性的初步研究[J]. 水运工程, 2010(8): 76-80. WANG Y H, WANG C H, LIU D B, et al. Preliminary study on channel stability in Qinzhou Bay[J]. Port & Waterway Engineering, 2010(8): 76-80. |
| [10] |
王玉海. 钦州湾滩槽地貌体系演化数值模拟研究[J]. 水运工程, 2013(1): 45-50. WANG Y H. Numerical modeling morphodynamics of channel-shoal system in Qinzhou Bay[J]. Port & Waterway Engineering, 2013(1): 45-50. |
| [11] |
董德信, 李谊纯, 陈宪云, 等. 海洋工程对钦州湾岸线地形及泥沙冲淤的影响[J]. 广西科学, 2015, 22(3): 266-273. DONG D X, LI Y C, CHEN X Y, et al. Impacts of ocean engineering on shoreline, topography and deposition-erosion environment in Qinzhou Gulf[J]. Guangxi Sciences, 2015, 22(3): 266-273. |
| [12] |
孙永根, 丰爱平, 王恩康, 等. 钦州湾悬浮泥沙特征[J]. 海洋地质与第四纪地质, 2016, 36(1): 79-86. SUN Y G, FENG A P, WANG E K, et al. Characters of the suspended load in Qinzhou Bay[J]. Marine Geology & Quaternary Geology, 2016, 36(1): 79-86. |
| [13] |
ZU T T, GAN J P, EROFEEVA S Y. Numerical study of the tide and tidal dynamics in the South China Sea[J]. Deep-Sea Res Ⅰ, 2008, 55: 137-154. DOI:10.1016/j.dsr.2007.10.007 |
| [14] |
VAN RIJN L C. Sediment transport, part Ⅱ:Suspended load transport[J]. Journal of Hydraulic Engineering, 1984, 110(11): 1613-1641. DOI:10.1061/(ASCE)0733-9429(1984)110:11(1613) |
| [15] |
张瑞瑾. 河流泥沙动力学[M]. 北京: 中国水利水电出版社, 1998. ZHANG R J. River sediment dynamics[M]. Beijing: China Water Power Press, 1998. |
| [16] |
钱宁, 万兆惠. 泥沙运动力学[M]. 北京: 科学出版社, 1983. QIAN N, WAN Z H. Mechanics of sediment transport[M]. Beijing: Science Press, 1983. |
 2018, Vol. 25
2018, Vol. 25 


