2. 钦州学院,钦州市港口航道与海岸工程重点实验室,广西钦州 535011
2. Key Laboratory of Habor, Coastal and Offshore Engineering, Qinzhou University, Qinzhou, Guangxi, 535011, China
我国河口、海岸区多为粉沙淤泥覆盖,在风浪掀沙和潮流输沙作用下,有较多泥沙悬浮和输移。目前,我国已着手开展全国海岸和近岸海域整治与修复工作,其中一项重要内容即近岸海域泥沙输运及底床冲淤演变规律的研究。泥沙输运过程影响海洋地貌演变,是河口、近海海洋工程中的重要问题。海洋生态动力过程中,泥沙输运过程影响碳、营养物和污染物的输运和吸收、生物多样性等。悬浮颗粒消弱光,限制初级生产力,改变海洋生态系统。而近底水沙交界面附近沉积层的再悬浮过程,释放营养通量、颗粒有机氮,进而影响海洋生态循环过程[1]。对于水沙交界面附近(图 1)的淤积率D和冲刷率E,国外学者做了大量的实验和现场测量[2-7]。底沙与悬沙以何种方式进行交换,在悬沙与底床泥沙的交换过程中,冲刷的同时是否伴随着悬沙的淤积,淤积和冲刷究竟是怎样的一个过程等均有待进一步的探讨,这对于了解近底泥沙通量至关重要。对于非粘颗粒泥沙,淤积和冲刷的同步性已经较为明确,由于较大的颗粒粒径和颗粒密度,水流无法一直保持泥沙颗粒的悬浮,所以采用Einstein建议的公式(E-D)[8]。但对于粘性细颗粒泥沙,淤积与冲刷的同步性问题一直处于争论过程,需要进一步分析研究。本文从近底泥沙通量描述方法出发,在分析总结几个泥沙系列实验基础上,认为细颗粒泥沙淤积与冲刷过程是同时发生的,从而进一步完善了水沙界面处泥沙交换现象的物理图谱。

|
图 1 水沙交界面 Fig.1 The exchange interface of water and sediment |
近底泥沙通量即悬沙和底沙的交换,是不平衡输沙的一个关键问题,至今尚未彻底解决。确定含沙量s的关键问题是确定近底泥沙通量Fs。悬沙运动方程的底部边界条件,即近底泥沙通量为[9-10]
| $ {F_s} = - \omega {s_{ - H}} - {{\rm{ \mathsf{ ε} }}_z}\frac{{\partial s}}{{\partial z}}{{\rm{|}}_{ - H}}{\rm{。}} $ | (1) |
将公式(1)简化为
| $ {F_s} = {\alpha _1}\omega {s^*} - {\alpha _2}\omega {s_0} = - \alpha \;\omega ({s_0} - {s^*}), $ | (2) |
式中,α1、α2和α为系数,S0为悬沙浓度,S*为挟沙力,ω为泥沙沉速。
对于挟沙力方法,当悬沙浓度s0大于挟沙力s*时,底床发生淤积;反之,则冲刷;相等时处于微冲微淤的平衡状态。
1.2 切应力方法切应力方法描述近底泥沙通量Fs的一般形式为
| $ {F_s} = \left\{ \begin{array}{l} \omega {s_0}{P_{dep}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\tau _b} \le {\tau _{cd}}\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\tau _{cd}} < {\tau _b} < {\tau _{ce}}\\ M({\tau _b}/{\tau _{ce}} - 1)\;\;\;\;\;\;{\tau _b} \ge {\tau _{ce}} \end{array} \right., $ | (3) |
式中,Pdep=(1-τb/τcd)为沉降概率,τb为底部切应力,τcd为临界淤积切应力,τce为临界冲刷切应力,M为冲刷系数。
切应力方法物理意义较为明确:当水体底部切应力大于临界冲刷切应力时,床面发生冲刷;当底部切应力小于临界淤积切应力时,底床淤积;其他情况则处于不冲不淤的平衡状态。
1.3 统一形式李瑞杰等[11]认为从悬沙运动方程和近底泥沙通量Fs本身物理意义来讲,挟沙力和切应力方法是一致的。两者均表征悬沙运动的特性,以及由近底泥沙通量引起的水体中含沙量的变化,都能够准确描述泥沙冲刷平衡过程。因此,两种方法之间必然存在某种关系。罗锋[10]对近底泥沙通量的不同提法及各自的不同描述作了详细的回顾和总结,并进行了归类分析。
| $ {F_s} = \left\{ \begin{array}{l} {\alpha _d}\omega {s_0}(\frac{{{s^*}}}{{{s_d}}} - 1)\;\;\;\;\;\;\;\;\;\;{s^*} \le {s_d}\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{s_d} < {s^*} < {s_e}\\ {\alpha _e}\omega {s_0}(\frac{{{s^*}}}{{{s_e}}} - 1)\;\;\;\;\;\;\;\;\;\;{s^*} \ge {s_e} \end{array} \right., $ | (4) |
式中,αe为冲刷系数,αd为沉降系数;sd*、se*为近底临界挟沙力,等于临界状态下的近底含沙量sd、se。
从式(4)可以看出,若sd=se=s0,αd=αe=α,则式(4)即简化为式(2)成为常用的挟沙力公式,即挟沙力方法和切应力方法从形式上是统一的。可以看出,两种方法既可以准确描述同一物理现象,又有统一的数学表达形式,两者之间存在一定的一致性。两者均表征悬沙运动的特性,以及由近底泥沙通量引起的水体中含沙量的变化,都能够准确描述泥沙冲刷平衡过程。
2 淤积与冲刷的同步性探讨 2.1 系列经典实验分析目前,广泛应用的粘性泥沙的淤积率公式基于两个系列沉积实验。最早由Krone[12]设计直水槽实验实现,水槽长33 m,宽1 m,水深为0.33 m;随后由Partheniades等[13-14]、Mehta等[15-16]、Kuijper等[3]学者在环形水槽中实现。这里重新回顾几个系列实验的发生条件[5-6, 17],并对结论做进一步研究。
Krone[12]通过直水槽系列实验拟合普适公式:
| $ \begin{array}{l} \frac{{dh\overline s }}{{dt}} = - D{\rm{ }} = - {\omega _s}{C_{bed}}{P_{dep}},{\tau _b} < {\tau _{cd}};\\ {P_{dep}} = \left\{ \begin{array}{l} (1 - {\tau _b}/{\tau _{cd}})\\ 0 \end{array} \right.,\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {{\tau _b} < {\tau _{cd}}}\\ {{\tau _b} \ge {\tau _{cd}}} \end{array}{\rm{。}} \end{array} $ | (5) |
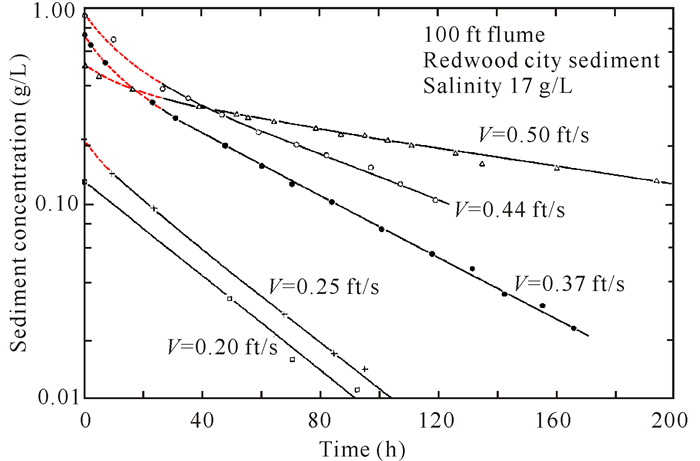
该公式认为所有泥沙在一定流速条件下, 即τb < τcd时沉降(图 2)。Nowell等[17]在中性和非中性化学条件下,做了不同粒径非粘性粉沙颗粒的冲刷和沉降实验,观测到临界淤积切应力和临界冲刷切应力不同,τb>τce时泥沙不再沉降。然而这个实验是在层流条件下进行的,不能清晰地解释紊流特性下的现象。Partheniades[18]通过旋转环形水槽3组实验,认为沉积和冲刷不会同时发生。其中,第一组为环形水槽在一定旋转速度下的淤积实验,达到平衡浓度后,将含有悬沙的水换成清水,相同的实验条件下发现清水未发生变化,由此得出:淤积条件下,不会发生冲刷;第二组实验和第一组类似,但只是将含有悬沙的水部分换成清水,相同条件下新的平衡浓度变小;第三组实验中,底床在另一转速下冲刷,达到平衡条件后悬沙包含有冲刷的底沙,换成清水后没有变化,由此认为:冲刷条件下不会发生淤积。
Mehta等[2]的直水槽实验发现悬沙未完全沉降,Kuijper等[3]在有限长的直水槽中也出现类似的现象。Mehta等[15-16]通过环形水槽实验也发现,当τb < τcd时,并不是所有的泥沙淤积,而是形成一个平衡浓度。Mehta和Lott[4]在假定一定粒径条件下,对Krone[12]的公式重新分析;随后Verbeek等[5]利用连续的ωs和τcd值成功得出类似的结论;Teeter[6]利用多组份模型区别粘性颗粒和非粘性粉沙颗粒,可以得出Mehta等[15-16]的结论。
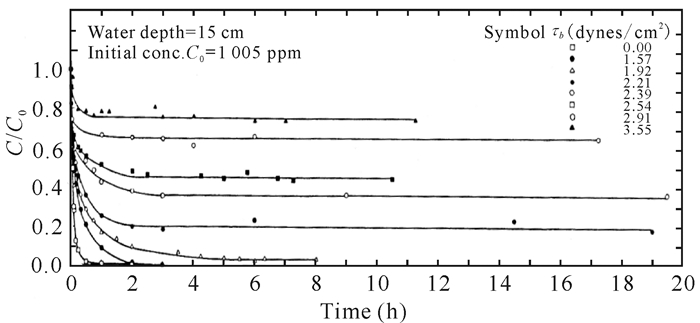
第二系列的沉降实验在环形水槽进行,较早由Partheniades及其团队[13-14]实现,随后Mehta等[15-16]和Kuijper等[3]也实现。Mehta等[15-16]和Partheniades等[13-14]设计的旋转环形水槽宽0.2 m,深0.45 m,平均直径1.5 m。得出了与Krone[12]实验相反的结论:当τb < τcd时,并非所有泥沙发生淤积,而是形成一个平衡浓度(图 3)。
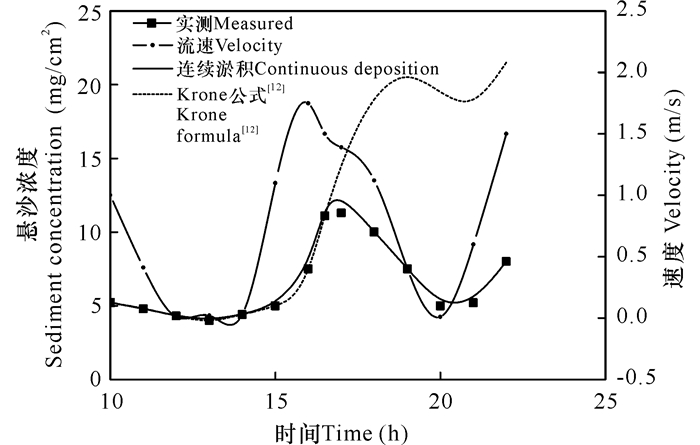
2.2 悬沙的连续沉降Sanford和Halka[7]分析了一系列Chesapeake湾潮流条件下的现场测量结果,发现潮流开始减速时,悬沙浓度开始减小,而这无法用Krone[12]的淤积公式描述。因为由Krone[12]的淤积公式和冲刷公式计算的悬沙浓度将会增加,直到底床切应力(水流速度)减小到临界淤积切应力(τb < τcd),如图 4所示。Sanford和Halka[7]在Long Island Sound、San Francisco Bay、Eastern Scheldt以及许多英国的河口分析得出相同的结论。
|
图 4 实测和计算含沙量比较 Fig.4 Measured and predicted total suspended sediment concentration |
分析我国瓯江河口流速和含沙量的现场测量,以及数值模拟结果,考虑悬沙的连续沉降可以较好地模拟瓯江河口含沙量场和泥沙输运特征[19]。若淤积公式采用公式(6),即认为悬沙连续沉降,则克服了Krone[12]淤积公式应用于河口、海岸水域时的偏离现象,能较好地模拟观测结果(图 4)。淤积率D表达为底床淤积泥沙通量:
| $ \begin{array}{*{20}{l}} {D = {\omega _s}{C_{bed}}, } \end{array} $ | (6) |
式中,Cbed和ωs分别为底床水沙交界面附近的悬沙浓度和沉降速度,公式(6)中可以考虑垂向浓度梯度对Cbed的影响,及絮凝对ωs的影响。
2.3 同步性探讨基于Krone[12]经典普适公式的切应力公式(3)及统一公式(4)表明近底泥沙冲刷和淤积不会同时发生。从经典系列实验条件及结论分析,冲刷和淤积不能同时发生只是在实验条件下合理,Krone[12]的数据的精度有待考究,特别是光滑水槽的床面切应力很难测量,τb小的误差会有实质性的影响[20]。然而随后的诸多实验,并未发现完全沉降现象,冲刷和淤积可能同时存在。
结合Sanford等[7]在一些河口、海湾的分析,认为近底水沙交界面附近,沉降始终是发生的,即水沙交界面附近淤积和侵蚀同时发生。从二维悬沙扩散方程的推导过程来看,方程中可以直观地看出,挟沙力方法实际为净通量,即冲刷和淤积是同时发生的。
同时,由于新淤积泥沙容易发生再悬浮,而这种现象在物理概念上是再悬浮过程。由于水槽中泥沙的沉降速度很小,垂向几乎无浓度梯度;低浓度(<0.3 g/L)下,淤积通量小于潜在的冲刷通量,可以解释Krone[12]的淤积实验中的沉降曲线问题。
同时,由于新淤积泥沙容易发生再悬浮,而这种现象在物理概念上是再悬浮过程。由于水槽中泥沙的沉降速度很小,垂向几乎无浓度梯度;低浓度(<0.3 g/L)下,淤积通量小于潜在的冲刷通量,可以解释Krone[12]的淤积实验中的沉降曲线问题。
水沙交界面处的泥沙交换机理应为:自然界床面切应力是随机的,可以利用偏斜概率密度函数[20]描述;新淤积的粘性泥沙的可冲刷性随着时间减小,而临界冲刷切应力由于固结和物理-化学效应随着时间增大。
3 结论“冲刷和淤积不能同时发生”的结论强烈依赖于实验条件,不能解释现场测量结果;另外,物理过程上也不能圆满解释冲刷和淤积不能同时发生的问题。实际工程应用中,由Krone[12]淤积公式和Partheniades等[13-14]冲刷共同确定的水沙交换过程可能不能正确描述其物理过程。
从二维悬沙扩散方程的推导过程来看,挟沙力方法实际为净通量,即冲刷和淤积是同时发生的;Mehta等[15-16],Kuijper等[3],Verbeek等[5],Teeter[6],Partheniades等[13-14]的实验过程也显示冲刷和淤积可能同时存在。
不同于经典的粘性泥沙理论,冲刷和淤积同时发生,即Fs=E-D;考虑冲刷和淤积过程的同步性,近底水沙交界面淤积公式采用D=ωsCbed,即认为水沙交界面泥沙连续沉降,新淤积细颗粒泥沙容易发生再悬浮[12]。
对于冲刷与淤积的同步性问题,进一步的工作将利用我国河口、海岸实测水文、泥沙资料展开分析,并从数值模拟角度分析连续淤积公式与实测资料的拟合关系。
| [1] |
陈长胜. 海洋生态系统动力学与模型[M]. 北京: 高等教育出版社, 2003. CHEN C S. Marine ecosystem dynamics and models[M]. Beijing: Higher Education Press, 2003. |
| [2] |
MEHTA A J, PARCHURE T M, DIXIT J G, et al. Resuspension potential of deposited cohesive sediments beds[C]//Proceedings of the Sixth Biennial International Estuarine Research Conference, Gleneden Beach, Oregon, November 1-6, 1981. New York: Academic Press, 1982: 591-609.
|
| [3] |
VERBEEK H, KUIJPER C, CORNELISSE J M, et al. Deposition of graded natural muds in the Netherlands[M]//MEHTA A J. Nearshore and estuarine cohesive sediment transport. American Washington DC: Geophysical Union, 2013: 185-204.
|
| [4] |
MEHTA A J, LOTT J W. Sorting of fine sediment during deposition[C]//Proceedings of the Conference on Advances in Understanding Coastal Sediment Processes. New York: Am Soc Civ Eng, 1987.
|
| [5] |
VERBEEK H, KUIJPER C, CORNELISSE J M, et al. Depostion of graded natural muds in the Netherlands[M]//MEHTA A J (ed. ). Nearshore and estuarine cohesive sediment transport. American Geophysical Union, Coastal and Estuarine Studies, 1993: 185-204.
|
| [6] |
TEETER A M. Clay-silt sediment modeling using multiple grain classes. Part Ⅱ: Application to shallow water resuspension and deposition[C]//MCANALLY W H, MEHTA A J (ed. ). Coastal and estuarine fine sediment processes. Elsevier, 2000, 3: 173-187.
|
| [7] |
SANFORD L P, HALKA J P. Assessing the paradigm of mutually exclusive erosion and deposition of mud, with examples from upper Chesapeake Bay[J]. Marine Geology, 1993, 114(1/2): 37-57. |
| [8] |
爱因斯坦. 明渠水流的挟沙能力[M]. 钱宁译. 北京: 水利出版社, 1956. EINSTEIN H A.The bed-load function for sediment transportation in open channel flows[M]. QIAN N (trans).Beijing:China Water & Power Press, 1956. |
| [9] |
丁平兴, 史峰岩, 孔亚珍. 波-流共同作用下的三维悬沙扩散方程[J]. 科学通报, 1999, 44(12): 1339-1342. DING P X, SHI F Y, KONG Y Z. Three-dimensional suspended sediment diffusion equations under the combined action of wave and flow[J]. Chinese Science Bulletin, 1999, 44(12): 1339-1342. DOI:10.3321/j.issn:0023-074X.1999.12.023 |
| [10] |
罗锋. 悬沙运动方程及其近底泥沙通量研究[D]. 南京: 河海大学, 2008. LUO F. Suspended sediment movement equation and its near-end sediment flux[D]. Nanjing: Hohai University, 2008. |
| [11] |
李瑞杰, 罗锋, 朱文谨. 悬沙运动方程及其近底泥沙通量[J]. 中国科学:E辑:技术科学, 2008, 38(11): 1995-2000. LI R J, LUO F, ZHU W J. Suspended sediment transport equation and its near-end sediment flux[J]. Science in China:Series E:Technological Sciences, 2008, 38(11): 1995-2000. |
| [12] |
EINSTEIN H A, KRONE R B. Experiments to determine modes of cohesive sediment transport in salt water[J]. Journal of Geophysical Research, 1962, 67(4): 1451-1461. DOI:10.1029/JZ067i004p01451 |
| [13] |
PARTHENIADES E, CROSS Ⅲ R H, AYORA A. Further results on the deposition of cohesive sediments[J]. Investigative Ophthalmology & Visual Science, 1968, 43(2): 1469. |
| [14] |
PARTHENIADES E. The present state of knowledge and needs for future research on cohesive sediment dynamies[C]//3rd International Symposium on River Sedimentation, School of Engineering, the University of Mississippi, University, 1986: 3-25.
|
| [15] |
MEHTA A J. On estuarine cohesive sediment suspension behavior[J]. Journal of Geophysical Research Oceans, 1989, 94(C10): 14303-14314. DOI:10.1029/JC094iC10p14303 |
| [16] |
MEHTA A J, PARTHENIADES E. An investigation of the depositional properties of flocculated fine sediments[J]. Journal of Hydraulic Research, 1975, 13(4): 361-381. DOI:10.1080/00221687509499694 |
| [17] |
NOWELL A R M, JUMARS P A, SELF R F L, et al. The effects of sediment transport and deposition on infauna: Results obtained in a specially designed flume[M]. LOPEZ G R, TAGHON G L, LEVINTON J S (eds. ). Ecology of marine deposit feeders. New York: Springer-Verlag, 1989: 247-268.
|
| [18] |
PATHENIADES E. Erosion and deposition of cohesive soils[J]. World Journal of Biological Psychiatry the Official Journal of the World Federation of Societies of Biological Psychiatry, 1965, 1(4): 190-192. |
| [19] |
刘金贵. 近岸泥沙输运工程及其三维数值模拟研究[D]. 南京: 河海大学, 2010. LIU J G. Study on sediment transport engineering and three-dimensional numerical simulation of nearshore[D]. Nanjing: Hohai University, 2010. |
| [20] |
WINTERWERP J C, VAN KESTEREN W G M. Introduction to the physics of cohesive sediment in the marine environment[M]. New York: Elsevier Science, 2005.
|
 2018, Vol. 25
2018, Vol. 25