【研究意义】 在状态反馈控制策略的设计中, 受控系统的状态是其重要的组成部分.许多控制系统的全部状态信息往往无法测量或者需要较大的测量成本.而状态观测器是基于部分量测信息重构原动态系统的状态的装置, 在反馈控制、故障诊断及系统监控等方面具有重要的应用[1-6]. 【前人研究进展】 基于观测器的控制策略更适用于解决这类系统的控制问题.而基于观测器的反馈控制的基本框架是先设计相应的状态观测器重构原系统的状态, 然后利用观测器的状态设计控制器以实现反馈控制.近年来, 基于观测器的控制设计问题已成为现代控制理论的研究热点之一.Yang[7]和Lin等[8]研究范数有界的不确定系统基于观测器的反馈镇定问题, 并以矩阵不等式给出了闭环系统的稳定性判据.Lien[9]采用线性矩阵不等式(LMI)方法, 研究了参数不确定性的线性系统基于观测器的反馈控制问题, 并给出基于LMI的控制器设计算法.Abolmasoumi等[10]基于模式相关的Lyapunov泛函研究Markov跳变系统基于观测器的H∞控制问题.Chen等[11-12]提出脉冲观测器和自适应脉冲观测器, 研究了不确定系统的输出反馈控制问题, 并给出控制器的参数化设计算法. 【本研究切入点】在实际系统中, 受控系统的量测输出总会受到随机噪声的干扰[13].随机噪声的存在, 可能会导致观测器无法重构原系统的状态, 进而无法设计有效的控制器.上述文献中, 量测输出存在的不确定性均要求满足范数有界条件.在分析与设计中, 不确定性与随机扰动不同, 前者直接采用标准的鲁棒控制技术处理, 后者的研究方法较为复杂, 有卡尔曼滤波理论、高斯滤波算法、最小方差滤波算法及多项式滤波方法等.然而, 这些方法一般只考虑离散系统.而且卡尔曼滤波和高斯滤波通常将随机干扰作为加性噪声处理.实际控制系统中, 乘性量测噪声也是不容忽视的.如吴骁航等[14]指出, 由于受到闪烁效应的影响, 机动目标跟踪系统的测量输出会产生乘性噪声. 【拟解决的关键问题】 本文针对具有乘性噪声测量输出的线性时不变系统, 讨论基于观测器的反馈控制器设计问题.首先, 对具有白噪声测量输出的线性系统, 设计相应的观测器.其次, 构造误差系统与受控系统复合的闭环系统, 并将其建模为Itô型随机微分方程.引入幂次复合型Lyapunov函数, 建立了该随机系统的均方稳定性和几乎必然稳定性的判别准则.同时给出了观测器增益矩阵与控制器增益矩阵的设计算法.最后, 通过小车上的倒立摆验证了本文所提出方法的有效性.
符号说明:矩阵P>0(≥0, < 0, ≤0)表示P为正定(半正定、负定、半负定)矩阵; E表示数学期望; Prob{A}表示事件A发生的概率; λmax (P), λmin(P)分别表示矩阵P的最大和最小特征值; ‖·‖表示为欧几里德范数.
1 问题描述考虑线性时不变系统:
| $ \left\{ \begin{array}{l} \dot x\left( t \right) = Ax\left( t \right) + Bu\left( t \right),\\ x\left( {{t_0}} \right) = {x_0}, \end{array} \right. $ | (1) |
其中, x(t)∈ ℝn为系统的状态向量; A∈ ℝn×n为已知的常系数矩阵; B∈ ℝn×m, m < n为系统的控制输入矩阵; u(t)∈ ℝm×n为系统的控制输入; x0∈ ℝn为系统的初值.本文考虑该系统的状态测量输出受到随机噪声干扰, 并具有如下形式:
| $ y\left( t \right) = Cx\left( t \right) + Dx\left( t \right)\xi \left( t \right), $ | (2) |
其中C, D∈ ℝmo×n为常数矩阵; ξ(t)∈ ℝ为状态测量中产生的白噪声, 满足如下假设:
(H) 噪声过程{ξ(t)}t≥t0满足
针对系统(1)及测量输出(2), 设计基于观测器的控制器如下:
| $ \left\{ \begin{array}{l} \dot {\hat x}\left( t \right) = A\hat x\left( t \right) + Bu\left( t \right) + L\left( {\hat y\left( t \right) - y\left( t \right)} \right),\\ \hat y\left( t \right) = C\hat x\left( t \right),\\ u\left( t \right) = K\hat x\left( t \right),\\ \hat x\left( {{t_0}} \right) = {{\hat x}_0}. \end{array} \right. $ | (3) |
其中,
定义误差系统e(t)=
| $ \left\{ \begin{array}{l} \left[ \begin{array}{l} \dot e\left( t \right)\\ \dot x\left( t \right) \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {A + LC}&0\\ {BK}&{A + BK} \end{array}} \right]\left[ \begin{array}{l} e\left( t \right)\\ x\left( t \right) \end{array} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} 0&{ - LD}\\ 0&0 \end{array}} \right]\left[ \begin{array}{l} e\left( t \right)\\ x\left( t \right) \end{array} \right]\xi \left( t \right),\\ \left[ \begin{array}{l} e\left( {{t_0}} \right)\\ x\left( {{t_0}} \right) \end{array} \right] = \left[ \begin{array}{l} {e_0}\\ {x_0} \end{array} \right]. \end{array} \right. $ |
其中e0=
| $ \left\{ \begin{array}{l} {\rm{d}}z\left( t \right) = \bar Az\left( t \right){\rm{d}}t + \bar Dz\left( t \right){\rm{d}}w\left( t \right),\\ z\left( {{t_0}} \right) = {z_0}. \end{array} \right. $ | (4) |
至此, 系统(1)的控制问题归结为寻找合适的控制增益矩阵K和观测器矩阵L, 使得闭环随机系统(4)为全局渐近稳定性问题.注意到, 源于量测噪声驱动因素, 观测器(3)为随机系统, 其解为随机过程, 进而诱导受控系统(1)也是随机系统.因此, 不能单纯地从确定系统的角度分析系统(1)的稳定性问题, 相应的稳定性需要采用数学期望或者概率对其解的数字特征进行刻画.本文主要关注均方稳定性和几乎必然稳定性.为此, 根据文献[13], 给出随机系统的均方指数稳定性和几乎必然指数稳定性的定义.
定义1 称随机系统(4)是均方指数稳定的, 如果存在正标量M和γ, 使得
| $ E{\left\| {z\left( t \right)} \right\|^2} \le M{\left\| {{z_0}} \right\|^2}{e^{ - \gamma \left( {t - {t_0}} \right)}},\forall t \ge {t_0}. $ |
定义2 称随机系统(4)是几乎必然指数稳定的, 如果存在正标γ, 使得对任意z0∈ ℝn, 都有
| $ \mathop {\lim \sup }\limits_{t \to + \infty } \frac{1}{t}\ln \left\| {z\left( t \right)} \right\| \le \gamma ,{\rm{a}}.\;{\rm{s}}.. $ |
引入复合Lyapunov函数方法, 分析系统(4)的均方指数稳定性和几乎必然稳定性问题, 并在稳定性条件的基础上探索控制器的参数化设计方法.
定理1 考虑闭环系统(4).对给定的标量q∈(0, 1]及增益矩阵K和L, 若存在正定矩阵P∈ ℝ2n×2n, 及标量c, 使得如下线性矩阵不等式成立:
| $ \begin{array}{l} 0.5{c^2}\left( {1 - q} \right)P + P\bar A + {{\bar A}^{\rm{T}}}P + {{\bar D}^{\rm{T}}}P\bar D - c\left( {1 - } \right.\\ \left. q \right)\left( {P\bar D + {{\bar D}^{\rm{T}}}P} \right) < 0, \end{array} $ | (5) |
则闭环系统(4)是几乎必然指数稳定的.特别地, 当q=1时, 闭环系统(4)是均方指数稳定的.
为了证明定理1, 需要引入一个引理.
引理1 若随机微分方程(4)的初值满足z0≠0, 则它的解满足Prob{z(t; t0, z0)≠0, t≥t0}=1.
该引理可直接由文献[13]引理3.2得出.下面给出定理1的详细证明.
证明 一方面, 线性矩阵不等式(5)蕴含着, 存在充分小的γ>0使得
| $ \begin{array}{l} \mathit{\Xi }\left( \gamma \right) = \left[ {\gamma + 0.5{c^2}\left( {1 - q} \right)} \right]P + P\bar A + {{\bar A}^{\rm{T}}}P + \\ {{\bar D}^{\rm{T}}}P\bar D - c\left( {1 - q} \right)\left( {P\bar D + {{\bar D}^{\rm{T}}}P} \right) < 0. \end{array} $ | (6) |
另一方面, 若z0=0, 则z(t)=0.因此我们只需证明当z0≠0, z(t)→0.由引理1得, 对任意的非零初值, 系统(4)中几乎所有的样本解都满足非零性.所以, 针对闭环系统(4), 引入复合Lyapunov函数W(t)=eqγ(t-t0)[V(t)]q, 其中V(t)
| $ {\rm{d}}V\left( t \right) = LV\left( {z\left( t \right)} \right){\rm{d}}t + HV\left( {z\left( t \right)} \right){\rm{d}}w\left( t \right), $ | (7) |
其中LV(z)=zT[PA+ATP+DTPD]z及HV(z)=zT[PD+DTP]z.对W(t)沿着随机微分方程(7)的轨线利用Itô公式, 得到
| $ \begin{array}{l} {\rm{d}}W\left( t \right) = q{e^{q\gamma \left( {t - {t_0}} \right)}}{V^{q - 1}}\left( t \right)\left[ {\gamma V\left( t \right) + LV\left( t \right) + } \right.\\ \left. {\frac{1}{2}\left( {q - 1} \right)\frac{{{{\left[ {HV\left( {z\left( t \right)} \right)} \right]}^2}}}{{V\left( t \right)}}} \right]{\rm{d}}t + \\ q{e^{q\gamma \left( {t - {t_0}} \right)}}{V^{q - 1}}\left( t \right)HV\left( {z\left( t \right)} \right){\rm{d}}w\left( t \right) = \\ q{e^{q\gamma \left( {t - {t_0}} \right)}}{V^{q - 1}}\left( t \right)\left[ {\gamma V\left( t \right) + LV\left( t \right) + \frac{1}{2}{c^2}\left( {1 - q} \right)V\left( t \right) - } \right.\\ c\left( {1 - q} \right)HV\left( {z\left( t \right)} \right) - \frac{1}{2}\left( {1 - } \right.\\ \left. q \right)\frac{{{{\left[ {HV\left( {z\left( t \right)} \right) - cV\left( t \right)} \right]}^2}}}{{V\left( t \right)}}{\rm{d}}t + \\ q{e^{q\gamma \left( {t - {t_0}} \right)}}{V^{q - 1}}\left( t \right)HV\left( {z\left( t \right)} \right){\rm{d}}w\left( t \right). \end{array} $ |
再利用线性矩阵不等式(6)及上述不等式, 可以推出
| $ \begin{array}{l} {\rm{d}}W\left( t \right) \le q{e^{q\gamma \left( {t - {t_0}} \right)}}{V^{q - 1}}\left( t \right){z^{\rm{T}}}\left( t \right)\Xi \left( \gamma \right)z\left( t \right){\rm{d}}t + \\ q{e^{q\gamma \left( {t - {t_0}} \right)}}{V^{q - 1}}\left( t \right)HV\left( {z\left( t \right)} \right){\rm{d}}w\left( t \right) \le \\ q{e^{q\gamma \left( {t - {t_0}} \right)}}{V^{q - 1}}\left( t \right)HV\left( {z\left( t \right)} \right){\rm{d}}w\left( t \right). \end{array} $ | (8) |
对不等式(8)两边从t0到t积分并取数学期望, 则有EW(t)≤W(t0), 从而有
| $ E{\left\| {z\left( t \right)} \right\|^{2q}} \le {\left[ {{\lambda _{\max }}\left( P \right)/{\lambda _{\min }}\left( P \right)} \right]^q}\left\| {{z_0}} \right\|{e^{ - q\gamma \left( {t - {t_0}} \right)}}. $ | (9) |
所以闭环系统(4)是全局2q阶矩指数稳定.由文献[13]定理4.2知, 闭环系统(4)为全局几乎必然指数稳定.显然, 当q=1时, 闭环系统(4)是全局均方指数稳定.
注1 从定理1的条件可以看出, 当p∈(0, 1)时, 扩散项可能对系统的稳定性起镇定作用.这反映了信道中的测量噪声不完全对系统起破坏作用的现象.
定理2 考虑具有测量输出(2)的线性系统(1)以及基于观测器的反馈控制器(3).对给定的标量q∈(0, 1], 若存在n×n阶矩阵P1>0, P2>0, n×m0阶矩阵L及标量c, 使得如下矩阵不等式成立:
| $ \left[ {\begin{array}{*{20}{c}} {{\Psi _1} + \bar LC + {C^{\rm{T}}}{{\bar L}^{\rm{T}}}}&{{K^{\rm{T}}}{B^{\rm{T}}}{P_2} + c\left( {1 - q} \right)\bar LD}&0\\ * &{{\Psi _2} + {P_2}BK + {K^{\rm{T}}}{B^{\rm{T}}}{P_2}}&{{D^{\rm{T}}}{{\bar L}^{\rm{T}}}}\\ *&* &{ - {P_1}} \end{array}} \right] < 0, $ | (10) |
其中Ψi=0.5c2(1-q)Pi+PiA+ATPi, i=1, 2, 则基于观测器的反馈控制器(3)能够几乎必然指数镇定系统(1).特别地, 当q=1时, 基于观测器的反馈控制器(3)能够均方指数镇定系统(1).相应的控制增益矩阵和观测器增益矩阵分别为K和L=P1-1L.
证明 令P=diag(P1, P2)及L=P1L, 利用Schur补引理即可证明矩阵不等式(10)等价于(5)式.
定理2的条件是关于矩阵变量P2和K的双线性矩阵不等式.因此, 不能直接用Matlab LMI工具箱求解.注意到矩阵不等式(10)中, 如果固定P2或K, 则它为LMI.利用这一点, 引入松弛变量设计交替优化算法[15]求解.即
Step 1:初始化q, c, l=0, P2=P20, 最大迭代次数N及足够大的正数υmax .
Step 2:求解如下优化问题
| $ \begin{array}{l} \min \upsilon = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{\nu _{ij}}} } ,\\ {\rm{subject}}\;{\rm{to}}\left\{ \begin{array}{l} {\rm{LMI}}\left( {10} \right),\\ - {\nu _{ij}} \le {k_{ij}} \le {\nu _{ij}},\\ {\nu _{ij}} \ge 0,\\ \;\;\;\;\;\;i = 1,2, \cdots ,m,j = 1,2, \cdots ,n. \end{array} \right. \end{array} $ | (11) |
其中K=(kij)m×n.如果优化问题有可行解, 则记为(υl, P1l, Kl, Ll).否则返回Step 1.
Step 3:如果υl≥υmax或者l≤N, 则停止, 输出K=Kl-1, L=(P1l-1)-1Ll-1.否则记υmax =υ, 并执行Step 4.
Step 4:令K=Kl, 求解LMI, 并记可行解为(P1l, P2l, Ll), 令P2=P2l, l=l+1, 返回Step 2.
注2 上述算法给出了控制增益矩阵和观测器增益矩阵的一种设计方法.然而该算法依赖于初值的选取.如果初值选取不合适, 可能导致优化问题(11)无可行解.为了避免这种情况, 可以采用非线性半定优化求解器PENLAB[16]求解.
3 数值实例考虑倒立摆的线性化模型:
| $ \begin{array}{l} A = \left[ {\begin{array}{*{20}{c}} 0&1&0&0\\ 0&{ - \frac{{\left( {I + m{l^2}} \right)b}}{p}}&{\frac{{{m^2}g{l^2}}}{p}}&0\\ 0&0&0&1\\ 0&{ - \frac{{mlb}}{p}}&{\frac{{mgl\left( {M + m} \right)}}{p}}&0 \end{array}} \right],\\ B = \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{{I + m{l^2}}}{p}}\\ 0\\ {\frac{{ml}}{p}} \end{array}} \right], \end{array} $ |
其中p=I(M+m)+Mml2, M=0.5 kg为小车的质量, m=0.5 kg为摆杆的质量, b=0.1 N/m/s为小车的摩察系数, I=0.006 kg·m2为摆杆惯量, l=0.3 m为摆杆转动轴心到质心长度, g=9.8 m/s2为重力加速度, x1表示小车的位置, x2表示小车的速度, x3表示摆动角度, x4表示其角速度.假设该倒立摆模型的测量输出满足(2), 其中C=[1 0 0 0], D=[1 1 0.6 0.1]×10-3.应用定理2并结合双线性矩阵不等式的求解算法, 可求解得到控制增益矩阵和观测器增益矩阵分别为
| $ \begin{array}{l} K = \left[ {\begin{array}{*{20}{c}} {0.88}&{1.25}&{ - 17.17}&{ - 1.15} \end{array}} \right],L = \\ {\left[ {\begin{array}{*{20}{c}} { - 14.33}&{ - 103.26}&{ - 97.73}&{ - 698.08} \end{array}} \right]^{\rm{T}}}. \end{array} $ |
数值仿真中, 选取初始条件x0=[0.3 -0.1 0 -0.5] T及
|
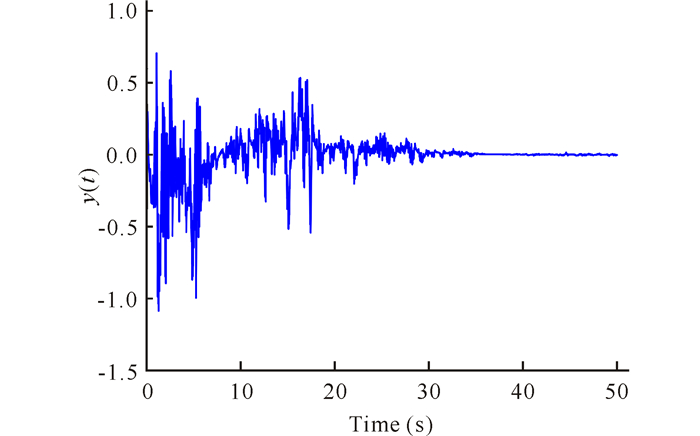
图 1 闭环系统的测量输出 Fig.1 The measured output of the closed-loop system |
|
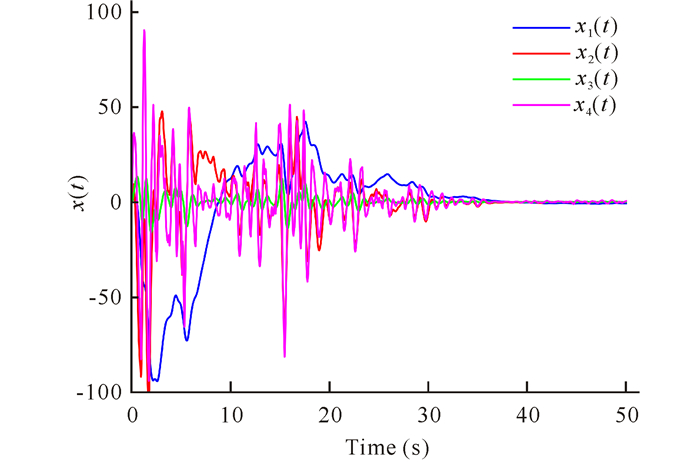
图 2 闭环系统的样本轨线 Fig.2 Sample path trajectories of the closed-loop system |
|
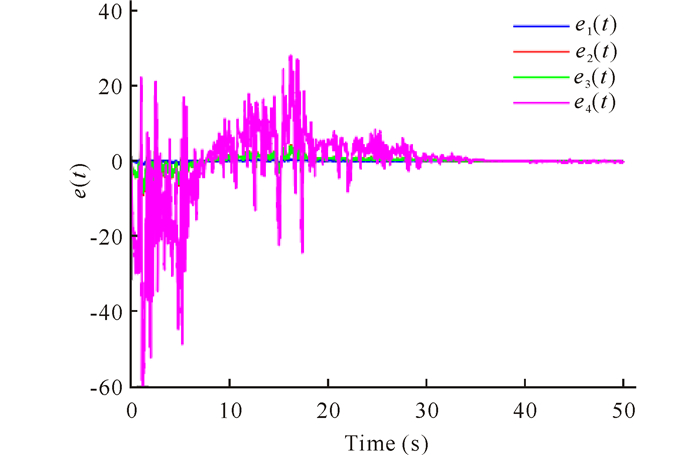
图 3 误差系统的样本轨线 Fig.3 Sample path trajectories of the error system |
本文研究了具有乘性量测噪声的线性系统基于观测器的输出反馈控制问题.利用复合Lyapunov函数方法, 建立了闭环系统的均方指数稳定性与几乎必然指数稳定性判据, 并给出了控制增益矩阵与观测器增益矩阵的设计算法.该稳定性判据揭示了量测噪声并不总是有害于系统的稳定性, 在几乎必然稳定意义下, 乘性量测噪声对系统稳定性起积极作用的客观规律.
| [1] |
SCHMITENDORF W E. Design of observer-based robust stabilizing controllers[J]. Automatica, 1988, 24(5): 693-696. DOI:10.1016/0005-1098(88)90117-3 |
| [2] |
HUANG G J, CHEN W H. A revisit to the design of switched observers for switched linear systems with unknown inputs[J]. International Journal of Control, Automation and Systems, 2014, 12(5): 954-962. DOI:10.1007/s12555-013-0121-x |
| [3] |
CHEN W H, LI D X, LU X. Impulsive observers with variable update intervals for Lipschitz nonlinear time-delay systems[J]. International Journal of Systems Science, 2013, 44(10): 1934-1947. DOI:10.1080/00207721.2012.670305 |
| [4] |
CHEN W H, LI D X, LU X. Impulsive functional observers for linear systems[J]. International Journal of Control, Automation and Systems, 2011, 9(5): 987. DOI:10.1007/s12555-011-0521-8 |
| [5] |
黄敢基, 罗世贤, 钟佳成. 线性系统的间歇观测器设计[J]. 广西科学, 2015, 22(4): 425-429. HUANG G J, LUO S X, ZHONG J C. Intermittent observer design for linear systems[J]. Guangxi Sciences, 2015, 22(4): 425-429, 437. |
| [6] |
沈艳军, 胡俊波. 一类非线性系统连续非光滑自适应观测器设计[J]. 广西科学, 2015, 22(4): 421-424. SHEN Y J, HU J B. Continuous but nonsmooth adaptive observer design for a class of nonlinear systems[J]. Guangxi Sciences, 2015, 22(4): 421-424. |
| [7] |
YANG S K, CHEN C L. Observer-based robust controller design for a linear system with time-varying perturbations[J]. Journal of Mathematical Analysis and Applications, 1997, 213(2): 642-661. DOI:10.1006/jmaa.1997.5566 |
| [8] |
LIN Z, GUAN X, LIU Y, et al. Observer-based robust control for uncertain systems with time-varying delay[J]. IMA Journal of Mathematical Control and Information, 2001, 18(3): 439-450. DOI:10.1093/imamci/18.3.439 |
| [9] |
LIEN C H. Robust observer-based control of systems with state perturbations via LMI approach[J]. IEEE Transactions on Automatic Control, 2004, 49(8): 1365-1370. DOI:10.1109/TAC.2004.832660 |
| [10] |
ABOLMASOUMI A H, MOMENI H R. Robust obse-rver-based H∞ control of a Markovian jump system with different delay and system modes[J]. International Journal of Control, Automation and Systems, 2011, 9(4): 768-776. DOI:10.1007/s12555-011-0419-5 |
| [11] |
CHEN W H, YANG W, LU X. Impulsive observerba-sed stabilisation of uncertain linear systems[J]. IET Control Theory & Applications, 2013, 8(3): 149-159. |
| [12] |
CHEN W H, YANG W, ZHENG W X. Adaptive impulsive observers for nonlinear systems:Revisited[J]. Automatica, 2015, 61: 232-240. DOI:10.1016/j.automatica.2015.08.018 |
| [13] |
MAO X. Stochastic differential equations and applications[M]. Chichester: Horwood Publishing, 2007.
|
| [14] |
吴骁航, 宋申民. 具有乘性噪声和随机量测时滞的目标跟踪算法[J]. 中国惯性技术学报, 2017, 25(1): 128-135. WU X H, SONG S M. Target tracking algorithm for system with multiplicative noises and randomly delayed measurements[J]. Journal of Chinese Inertial Technology, 2017, 25(1): 128-135. |
| [15] |
CHEN W H, JIANG Z, LU X, et al. H∞ synchronization for complex dynamical networks with coupling delays using distributed impulsive control[J]. Nonlinear Analysis:Hybrid Systems, 2015, 17: 111-127. DOI:10.1016/j.nahs.2015.02.004 |
| [16] |
FIALA J, KŎCVARA M, STINGL M. PENLAB: A MATLAB solver for nonlinear semidefinite optimization[J]. arXiv Preprint arXiv: 1311. 5240, 2013.
|
 2017, Vol. 24
2017, Vol. 24 


