2. 广西高校工业过程智能控制技术重点实验室,广西柳州 545006
2. Key Laboratory of Industrial Process Intelligent Control Technology of Guangxi Higher Education Institutes, Liuzhou, Guangxi, 545006, China
【研究意义】在自然界和许多工程领域中,存在诸多扩散耦合现象,特别是在生物化学工程、材料工程以及电力工程中。例如,化学反应器中物质的分布状态[1]、半导体材料中杂质的扩散过程[2]及电力传输线间的电磁耦合现象[3]。目前,人工智能技术蓬勃发展,扩散耦合的系统由于其在智能交通、网络通信、社会经济等各领域的广泛应用而受到高度重视[4-6]。扩散耦合的网络系统一般由偏微分方程所描述,可建模为具扩散耦合的偏微分系统。迭代学习控制是一种先进的智能跟踪控制算法,其基本思想是在有限时间区间上利用之前的控制经验去调节当前的控制输入以实现精确跟踪的目的[7]。自1984年由Arimoto开创性地提出迭代学习控制以来,其在理论分析和实际应用中均取得了丰硕的成果[8-11]。【前人研究进展】目前,对偏微分系统的学习跟踪控制分析框架大致如下:从分析方法来看,一类是简化模型的方法[12-14]。如Choi等[12]研究了将一类线性双曲型偏微分系统降阶成常微分系统,然后根据离散时间近似得到简化后的模型,进一步设计了开环P型控制器;Cichy等[13]考虑将抛物分布参数系统进行C-N离散化得到了偏差分系统,然后设计学习控制器并研究其轨迹跟踪问题;Xiao等[14]利用Galerkins方法及特征谱理论对拟线性偏微分系统进行模型简化,并相应地提出了基于特征谱的学习控制策略。另一类是建立系统输入输出关系[15-16]。由于迭代学习控制一般是基于输入和输出关系来设计控制器的,因而Huang等通过直接构建系统解的表达形式来设计P型学习控制器[15],又利用拉氏变换将时域内的偏微分系统变换到频域内,然后构建系统输入和输出关系设计迭代学习控制算法,进一步分析频域内的跟踪误差的学习收敛性[16]。从控制方式的角度来看,一类是分布式控制策略[17-19],根据所设计的分布式迭代学习控制器,对输出误差在L2范数意义下的收敛性进行分析。Dai等[18]针对不确定的线性抛物型偏微分系统设计了闭环P型学习律,并提出了跟踪误差的收敛性条件。另一类是边界控制策略[20-21]。Huang等[20]设计稳态P型迭代学习控制器,研究了一类单输入单输出拟线性偏微分方程的边界流速控制问题。许多工业控制过程中普遍存在时滞现象,时滞也是影响系统控制性能的重要因素。时滞系统在控制方面也有不少研究成果[22-24]。如Chen等[23]对具有状态时滞的非线性系统设计了可变区间的脉冲观测器。【本研究切入点】根据N个具有空间扩散耦合的定常偏微分时滞系统转换成超向量形式的等价学习系统。基于超向量形式的学习系统设计开闭环P型迭代学习控制器,然后研究系统跟踪误差的收敛性。最后,用数值仿真来验证所提学习算法的有效性。【拟解决的关键问题】 基于超向量形式的等价系统建立起迭代学习控制框架,并对其学习跟踪误差的收敛性进行分析,保证系统跟踪误差沿迭代轴方向收敛。
符号约定:n维列向量W=(w1, w2, …, wn)T的范数为
考虑如下N个扩散耦合的线性定常偏微分时滞系统:
| $ \left\{ \begin{array}{l} \frac{{\partial {Z^\alpha }\left( {x,t} \right)}}{{\partial t}} = {A_\tau }{Z^\alpha }\left( {x,t - {\tau _\alpha }} \right) + B{\nabla ^2}{Z^\alpha }\left( {x,t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{\alpha \ne i} {{D_{i\alpha }}{\nabla ^2}\left( {{Z^i}\left( {x,t} \right) - {Z^\alpha }\left( {x,t} \right)} \right)} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;H{u^\alpha }\left( {x,t} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1.{\rm{a}}} \right)\\ {y^\alpha }\left( {x,t} \right) = C{Z^\alpha }\left( {x,t} \right) + G{u^\alpha }\left( {x,t} \right),\;\;\;\;\;\;\;\;\;\left( {1.{\rm{b}}} \right) \end{array} \right. $ |
这里α=1, 2, …, N, 空间变量x=(x1, x2)T∈Ω⊂ℝ2,时间变量t∈[0, T],系统状态变量为Zα(·, ·)∈ℝn, uα(·, ·)∈ℝs为系统控制输入,yα(·, ·)∈ℝl为系统输出。Aτ∈ℝn×n, H∈ℝn×s, C∈ℝl×n, G∈ℝl×s是适维定常矩阵,B∈ℝn×n为扩散系数矩阵。时滞系数τα∈[0, τ](α=1, 2, …, N),其中τ为有界常数。Diα∈ℝn×n为N个状态变量间的耦合系数矩阵且满足Dαi=Diα, α≠i, i=1, …, N。
系统(1)对应的初边值条件如下:
| $ {Z^\alpha }\left( {x,t} \right) = 0,\left( {x,t} \right) \in \partial \mathit{\Omega } \times \left[ { - \tau ,T} \right], $ | (2) |
| $ {Z^\alpha }\left( {x,t} \right) = \varphi _0^\alpha \left( {x,t} \right),\left( {x,t} \right) \in \mathit{\Omega } \times \left[ { - \tau ,0} \right]。$ | (3) |
注记1:系统(1)由N个具有空间扩散耦合的偏微分系统组成,每个偏微分系统可表示现实世界中的网络的结点、生物神经元等,因而它可用来描述一类复杂网络系统,如互联网拓扑结构[4]、生物神经元网络[5]等。一般的,由于两个系统状态之间相对扩散耦合强度一致,所在这里要求耦合矩阵满足Dαi=Diα。
1.1 系统简化将α=1, 2, …, N分别代入式(1)中满足,
| $ \begin{array}{l} \frac{\partial }{{\partial t}}{Z^1}\left( {x,t} \right) = {A_\tau }{Z^1}\left( {x,t - {\tau _1}} \right) + B\Delta {Z^1}\left( {x,t} \right) + \\ {D_{12}}{\nabla ^2}\left( {{Z^2}\left( {x,t} \right) - {Z^1}\left( {x,t} \right)} \right) + {D_{13}}{\nabla ^2}\left( {{Z^3}\left( {x,t} \right) - } \right.\\ \left. {{Z^1}\left( {x,t} \right)} \right) \cdots + {D_{1N}}{\nabla ^2}\left( {{Z^N}\left( {x,t} \right) - {Z^1}\left( {x,t} \right)} \right) + \\ H{u^1}\left( {x,t} \right), \end{array} $ |
| $ {y^1}\left( {x,t} \right) = C{Z^1}\left( {x,t} \right) + G{u^1}\left( {x,t} \right), $ |
| $ \begin{array}{l} \frac{\partial }{{\partial t}}{Z^2}\left( {x,t} \right) = {A_\tau }{Z^2}\left( {x,t - {\tau _2}} \right) + B\Delta {Z^2}\left( {x,t} \right) + \\ {D_{21}}{\nabla ^2}\left( {{Z^1}\left( {x,t} \right) - {Z^2}\left( {x,t} \right)} \right) + {D_{23}}{\nabla ^2}\left( {{Z^3}\left( {x,t} \right) - } \right.\\ \left. {{Z^2}\left( {x,t} \right)} \right) \cdots + {D_{2N}}{\nabla ^2}\left( {{Z^N}\left( {x,t} \right) - {Z^2}\left( {x,t} \right)} \right) + \\ H{u^2}\left( {x,t} \right), \end{array} $ |
| $ {y^2}\left( {x,t} \right) = C{Z^2}\left( {x,t} \right) + G{u^2}\left( {x,t} \right), $ |
| $ \begin{array}{l} \frac{\partial }{{\partial t}}{Z^3}\left( {x,t} \right) = {A_\tau }{Z^3}\left( {x,t - {\tau _3}} \right) + B{\nabla ^2}{Z^3}\left( {x,t} \right) + \\ {D_{31}}{\nabla ^2}\left( {{Z^1}\left( {x,t} \right) - {Z^3}\left( {x,t} \right)} \right) + {D_{32}}\Delta \left( {{Z^2}\left( {x,t} \right) - } \right.\\ \left. {{Z^3}\left( {x,t} \right)} \right) \cdots + {D_{3N}}{\nabla ^2}\left( {{Z^N}\left( {x,t} \right) - {Z^3}\left( {x,t} \right)} \right) + \\ H{u^3}\left( {x,t} \right), \end{array} $ |
| $ {y^3}\left( {x,t} \right) = C{Z^3}\left( {x,t} \right) + G{u^3}\left( {x,t} \right), $ |
| $ \begin{array}{l} \frac{\partial }{{\partial t}}{Z^N}\left( {x,t} \right) = {A_\tau }{Z^N}\left( {x,t - {\tau _N}} \right) + B{\nabla ^2}{Z^N}\left( {x,t} \right) + \\ {D_{N1}}{\nabla ^2}\left( {{Z^1}\left( {x,t} \right) - {Z^N}\left( {x,t} \right)} \right) + {D_{N2}}{\nabla ^2}\left( {{Z^2}\left( {x,t} \right) - } \right.\\ \left. {{Z^N}\left( {x,t} \right)} \right) \cdots + {D_{NN - 1}}{\nabla ^2}\left( {{Z^{N - 1}}\left( {x,t} \right) - {Z^N}\left( {x,t} \right)} \right) + \\ H{u^N}\left( {x,t} \right), \end{array} $ |
| $ {y^N}\left( {x,t} \right) = C{Z^N}\left( {x,t} \right) + G{u^N}\left( {x,t} \right), $ |
引入如下超向量形式:
| $ u\left( {x,t} \right) = {\left[ {{u^1}\left( {x,t} \right),{u^2}\left( {x,t} \right), \cdots ,{u^N}\left( {x,t} \right)} \right]^{\rm{T}}}, $ |
| $ Z\left( {x,t} \right) = {\left[ {{Z^1}\left( {x,t} \right),{Z^2}\left( {x,t} \right), \cdots ,{Z^N}\left( {x,t} \right)} \right]^{\rm{T}}}, $ |
| $ \begin{array}{l} Z\left( {x,t - \tau } \right) = \left[ {{Z^1}\left( {x,t - {\tau _1}} \right),{Z^2}\left( {x,t - {\tau _2}} \right), \cdots ,} \right.\\ {\left. {{Z^N}\left( {x,t - {\tau _N}} \right)} \right]^{\rm{T}}},y\left( {x,t} \right) = \left[ {{y^1}\left( {x,t} \right),{y^2}\left( {x,t} \right), \cdots ,} \right.\\ {\left. {{y^N}\left( {x,t} \right)} \right]^{\rm{T}}}。\end{array} $ |
则上述N个扩散耦合的偏微分时滞系统可以表示成如下形式:
| $ \left\{ \begin{array}{l} \frac{{\partial Z\left( {x,t} \right)}}{{\partial t}} = {{\bar A}_\tau }Z\left( {x,t - \tau } \right) + \bar D{\nabla ^2}Z\left( {x,t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\bar Hu\left( {x,t} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {4,{\rm{a}}} \right)\\ y\left( {x,t} \right) = \bar CZ\left( {x,t} \right) + \bar Gu\left( {x,t} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {4,{\rm{b}}} \right) \end{array} \right. $ |
其中Z(·, ·)∈ℝnN, y(·, ·)∈ℝlN, u(·, ·)∈ℝsN,
| $ {{\bar A}_\tau } = \left[ {\begin{array}{*{20}{c}} {{A_\tau }}&{}&{}&{}\\ {}&{{A_\tau }}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{A_\tau }} \end{array}} \right], $ |
| $ \bar H = \left[ {\begin{array}{*{20}{c}} H&{}&{}&{}\\ {}&H&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&H \end{array}} \right],\bar B = \left[ {\begin{array}{*{20}{c}} B&{}&{}&{}\\ {}&B&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&B \end{array}} \right], $ |
| $ \bar C = \left[ {\begin{array}{*{20}{c}} C&{}&{}&{}\\ {}&C&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&C \end{array}} \right],\bar G = \left[ {\begin{array}{*{20}{c}} G&{}&{}&{}\\ {}&G&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&G \end{array}} \right], $ |
| $ \begin{array}{l} \bar D = \\ \left[ {\begin{array}{*{20}{c}} {B - \sum\limits_{\alpha \ne 1} {{D_{1\alpha }}} }&{{D_{12}}}& \cdots &{{D_{1N}}}\\ {{D_{21}}}&{B - \sum\limits_{\alpha \ne N} {{D_{2\alpha }}} }& \cdots &{{D_{2N}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{D_{N1}}}&{{D_{N2}}}& \cdots &{B - \sum\limits_{\alpha \ne N} {{D_{N\alpha }}} } \end{array}} \right]。\end{array} $ |
则系统(4)对应的初边值条件如下:
| $ Z\left( {x,t} \right) = 0,\left( {x,t} \right) \in \partial \mathit{\Omega } \times \left[ { - \tau ,T} \right], $ | (5) |
| $ Z\left( {x,t} \right) = {\varphi _0}\left( {x,t} \right),\left( {x,t} \right) \in \mathit{\Omega } \times \left[ { - \tau ,0} \right]。$ | (6) |
这里φ0(·, ·)∈ℝnN。
1.2 问题陈述及准备对于具扩散耦合偏微分时滞系统(4),假设它在有限时间T内是可重复运行的,则该学习系统满足如下形式:
| $ \left\{ \begin{array}{l} \frac{{\partial {Z_k}\left( {x,t} \right)}}{{\partial t}} = {{\bar A}_\tau }{Z_k}\left( {x,t - \tau } \right) + \bar D\Delta {Z_k}\left( {x,t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\bar H{u_k}\left( {x,t} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {7,{\rm{a}}} \right)\\ {y_k}\left( {x,t} \right) = \bar C{Z_k}\left( {x,t} \right) + \bar G{u_k}\left( {x,t} \right),\;\;\;\;\;\;\;\;\;\;\;\;\left( {7,{\rm{b}}} \right) \end{array} \right. $ |
这里k为迭代次数,满足k=1, 2, 3, …。
本研究的控制目标是寻找期望输入ud(x, t),使得对于系统给定的期望输出yd(x, t),通过在有限的运行时间内不断地迭代使得系统实际输出yk(x, t)与期望输出相对应。
由于系统模型的无穷维特性,这使得对系统的控制有一定的难度,为了寻找控制输入序列{uk(x, t)},最终使得
| $ {u_{k + 1}}\left( {x,t} \right) = {u_k}\left( {x,t} \right) + \Gamma \left( t \right){e_k}\left( {x,t} \right) + L\left( t \right){e_{k + 1}}\left( {x,t} \right), $ | (8) |
式中,Γ(t), L(t)是待确定的学习增益矩阵,输出误差ek(x, t)定义为yd(x, t)-yk(x, t)。
假设1 在迭代学习过程中,学习系统(7)的初边值条件可被重置,即
| $ {Z_k}\left( {x,t} \right) = 0,\left( {x,t} \right) \in \partial \mathit{\Omega } \times \left[ { - \tau ,T} \right], $ | (9) |
| $ {Z_k}\left( {x,t} \right) = {\varphi _0}\left( {x,t} \right) = {Z_d}\left( {x,t} \right) \in \mathit{\Omega } \times \left[ { - \tau ,0} \right]。$ | (10) |
假设2 针对给定的期望跟踪目标yd(x, t),存在唯一的控制输入ud(x, t), 使得:
| $ \left\{ \begin{array}{l} \frac{{\partial {Z_d}\left( {x,t} \right)}}{{\partial t}} = {{\bar A}_\tau }{Z_d}\left( {x,t - \tau } \right) + \bar D\Delta {Z_d}\left( {x,t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\bar H{u_d}\left( {x,t} \right),\\ {y_d}\left( {x,t} \right) = \bar C{Z_d}\left( {x,t} \right) + \bar G{u_d}\left( {x,t} \right), \end{array} \right. $ |
下面给出引理1,这对后面定理的证明过程起到了重要的作用。
引理1[5]假设U={x:|xi| < li}(i=1, 2), n维向量函数z(x)∈C2(U)且在z(x)|əU=0,则满足下式:
| $ \int_U {{z^{\rm{T}}}\left( x \right){\nabla ^2}z\left( x \right){\rm{d}}x} \le - \left( {\frac{1}{{l_1^2}} + \frac{1}{{l_2^2}}} \right)\int_U {{z^{\rm{T}}}\left( x \right)z\left( x \right){\rm{d}}x} 。$ | (11) |
为了下节定理证明的简洁性,引入如下的标记:
| $ {{\bar u}_k}\left( {x,t} \right) \buildrel \Delta \over = {u_{k + 1}}\left( {x,t} \right) - {u_k}\left( {x,t} \right), $ |
| $ {{\bar Z}_k}\left( {x,t} \right) \buildrel \Delta \over = {Z_{k + 1}}\left( {x,t} \right) - {Z_k}\left( {x,t} \right)。$ |
首先,对定常系数的具扩散耦合的偏微分时滞系统采用开闭环P型学习律,给出输出误差的收敛条件,然后推广到时变系统的情况。最后,分析开环P型学习律下的误差收敛性。
2.1 定常系数的扩散耦合系统对定常的学习系统(7)利用开闭环P型学习律进行收敛性分析,给出定理1。
定理1 若可重复运行的定常学习系统(7)满足假设1~2,系统矩阵D≥0,开闭环学习控制器(8)中的增益矩阵Γ(t), L(t)满足如下不等式:
| $ {\left\| {{{\left( {I + \bar GL\left( t \right)} \right)}^{ - 1}}\left( {I + \bar G\Gamma \left( t \right)} \right)} \right\|^2} \le \rho ,2\rho \in \left[ {0,1} \right),\forall t\left[ {0,T} \right], $ | (12) |
则当迭代次数趋于无穷大时,系统跟踪误差的L2范数一致收敛到零,即
| $ \mathop {\lim }\limits_{k \to \infty } {\left\| {{e_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}} = 0,\forall t \in \left[ {0,T} \right]。$ |
证明 根据输出误差的定义及开闭环学习律(8)式,可得:
| $ \begin{array}{l} \;\;{e_{k + 1}}\left( {x,t} \right) = {e_k}\left( {x,t} \right) - {y_{k + 1}}\left( {x,t} \right) + {y_k}\left( {x,t} \right) = \\ {e_k}\left( {x,t} \right) - \bar C{Z_{k + 1}}\left( {x,t} \right) - \bar G{u_{k + 1}}\left( {x,t} \right) + \bar C{Z_k}\left( {x,t} \right) = \\ \bar G{u_k}\left( {x,t} \right), \end{array} $ |
| $ \begin{array}{l} {e_{k + 1}}\left( {x,t} \right) = {e_k}\left( {x,t} \right) - \bar C\left( {{Z_{k + 1}}\left( {x,t} \right) - {Z_k}\left( {x,t} \right)} \right) - \\ \bar G\left( {{u_{k + 1}}\left( {x,t} \right) - {u_k}\left( {x,t} \right)} \right) = \left( {I - \bar G\Gamma \left( t \right)} \right){e_k}\left( {x,t} \right) - \\ \bar C{{\bar Z}_k}\left( {x,t} \right) - \bar GL\left( t \right){e_{k + 1}}\left( {x,t} \right), \end{array} $ | (13) |
则可由(13)式得:
| $ \begin{array}{l} {e_{k + 1}}\left( {x,t} \right) = {\left( {1 + \bar GL\left( t \right)} \right)^{ - 1}}\left( {I - \bar G\Gamma \left( t \right)} \right){e_k}\left( {x,t} \right) - \\ {\left( {1 + \bar GL\left( t \right)} \right)^{ - 1}}\bar C{{\bar Z}_k}\left( {x,t} \right) = {{\bar e}_k}\left( {x,t} \right) + {{\bar C}_k}\left( {x,t} \right), \end{array} $ | (14) |
这里
| $ \begin{array}{l} {{\bar e}_k}\left( {x,t} \right) = {\left( {1 + \bar GL\left( t \right)} \right)^{ - 1}}\left( {I - \bar G\Gamma \left( t \right)} \right){e_k}\left( {x,t} \right),\\ {{\bar C}_k}\left( {x,t} \right) = - {\left( {1 + \bar GL\left( t \right)} \right)^{ - 1}}\bar C{{\bar Z}_k}\left( {x,t} \right)。\end{array} $ |
在(14)式两边同时左乘ek+1T(x, t),有
| $ \begin{array}{l} e_{k + 1}^{\rm{T}}\left( {x,t} \right){e_{k + 1}}\left( {x,t} \right) = \left( {{{\bar e}_k}\left( {x,t} \right) + } \right.\\ {\left. {{{\bar C}_k}\left( {x,t} \right)} \right)^{\rm{T}}}\left( {{{\bar e}_k}\left( {x,t} \right) + {{\bar C}_k}\left( {x,t} \right)} \right) \le 2\left( {\bar e_k^{\rm{T}}\left( {x,t} \right){{\bar e}_k}\left( {x,} \right.} \right.\\ \left. {\left. t \right) + \bar C_k^{\rm{T}}\left( {x,t} \right){{\bar C}_k}\left( {x,t} \right)} \right) = 2{\left\| {{{\bar e}_k}\left( {x,t} \right)} \right\|^2} + \\ 2{\left\| {{{\bar C}_k}\left( {x,t} \right)} \right\|^2} \le 2\rho {\left\| {{e_k}\left( {x,t} \right)} \right\|^2} + \\ 2{b_c}{\left\| {{{\bar Z}_k}\left( {x,t} \right)} \right\|^2}, \end{array} $ | (15) |
其中
对(15)式的空间变量x在Ω上进行积分,根据L2范数的定义有
| $ \begin{array}{l} \left\| {{e_{k + 1}}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 \le 2\rho \left\| {{e_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 + \\ 2{b_c}\left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2。\end{array} $ | (16) |
从式(16)易知,要估计‖ek+1(·, t)‖
根据(7.a)式,将第k+1次迭代过程减去第k次迭代过程可得:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {{Z_{k + 1}}\left( {x,t} \right) - {Z_k}\left( {x,t} \right)} \right) = \bar D\Delta \left( {{Z_{k + 1}}\left( {x,t} \right) - } \right.\\ \left. {{Z_k}\left( {x,t} \right)} \right) + \bar A\left( {{Z_{k + 1}}\left( {x,t - \tau } \right) - {Z_k}\left( {x,t - \tau } \right)} \right) + \\ H\left( {{u_{k + 1}}\left( {x,t} \right) - {u_k}\left( {x,t} \right)} \right), \end{array} $ | (17) |
并用(Zk+1(x, t)-Zk(x, t))T左乘(17)式两边,可以得到如下的表达式:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\bar Z_k^{\rm{T}}\left( {x,t} \right) - {{\bar Z}_k}\left( {x,t} \right)} \right) = \bar Z_k^{\rm{T}}\left( {x,t} \right)\bar D\Delta {{\bar Z}_k}\left( {x,t} \right) + \\ \bar Z_k^{\rm{T}}\left( {x,t} \right){{\bar A}_\tau }{{\bar Z}_k}\left( {x,t - \tau } \right) + \bar Z_k^{\rm{T}}\left( {x,t} \right){\overline {Hu} _k}\left( {x,t} \right), \end{array} $ |
上式两边分别对x在Ω上积分,得:
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2} \right) = 2\int_\mathit{\Omega } {\bar Z_k^{\rm{T}}\left( {x,t} \right)\bar D\Delta {{\bar Z}_k}\left( {x,} \right.} \\ \left. t \right){\rm{d}}x + 2\int_\mathit{\Omega } {\bar Z_k^{\rm{T}}\left( {x,t} \right){{\bar A}_\tau }{{\bar Z}_k}\left( {x,t - \tau } \right){\rm{d}}x} + \\ 2\int_\mathit{\Omega } {\bar Z_k^{\rm{T}}\left( {x,t} \right)H{{\bar u}_k}\left( {x,t} \right){\rm{d}}x} = {I_1} + {I_2} + {I_3}。\end{array} $ | (18) |
下面分别对Ii(i=1, 2, 3)进行处理。
根据定理1中系统矩阵D≥0,则存在一个矩阵Q使得D=QTQ。
对I1,运用引理1得:
| $ \begin{array}{l} {I_1} = 2\int_\mathit{\Omega } {\bar Z_k^{\rm{T}}\left( {x,t} \right)\bar D\Delta {{\bar Z}_k}\left( {x,t} \right){\rm{d}}x} = 2\int_\mathit{\Omega } {\bar Z_k^{\rm{T}}\left( {x,} \right.} \\ \left. t \right)\left( {{Q^{\rm{T}}}Q} \right)\Delta {{\bar Z}_k}\left( {x,t} \right){\rm{d}}x = - \left( {\frac{2}{{l_1^2}} + \frac{2}{{l_2^2}}} \right)\int_\mathit{\Omega } {\left( {Q{{\bar Z}_k}\left( {x,} \right.} \right.} \\ {\left. {\left. t \right)} \right)^{\rm{T}}}\left( {Q{{\bar Z}_k}\left( {x,t} \right)} \right){\rm{d}}x \le 0。\end{array} $ | (19) |
对I2有
| $ \begin{array}{l} {I_2} = 2\int_\mathit{\Omega } {\bar Z_k^{\rm{T}}\left( {x,t} \right){{\bar A}_\tau }{{\bar Z}_k}\left( {x,t - \tau } \right){\rm{d}}x} \le \\ {\lambda _{\max }}\left( {\bar A_\tau ^{\rm{T}}{{\bar A}_\tau }} \right)\left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 + \left\| {{{\bar Z}_k}\left( { \cdot ,t - \tau } \right)} \right\|_{{{\rm{L}}^2}}^2。\end{array} $ | (20) |
对I3,运用Höder不等式可得:
| $ \begin{array}{l} {I_3} = 2\int_\mathit{\Omega } {\bar Z_k^{\rm{T}}\left( {x,t} \right)\bar H{{\bar u}_k}\left( {x,t} \right){\rm{d}}x} \le \left\| {{{\bar Z}_k}\left( { \cdot ,} \right.} \right.\\ \left. {\left. t \right)} \right\|_{{{\rm{L}}^2}}^2 + {\lambda _{\max }}\left( {{{\bar H}^{\rm{T}}}\bar H} \right)\left\| {{{\bar u}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2。\end{array} $ | (21) |
通过式(18)—(21)可知,
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2} \right) \le \left( {1 + } \right.\\ \left. {{\lambda _{\max }}\left( {\bar A_\tau ^{\rm{T}}{{\bar A}_\tau }} \right)} \right)\left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 + \left\| {{{\bar Z}_k}\left( { \cdot ,t - \tau } \right)} \right\|_{{{\rm{L}}^2}}^2 + \\ {\lambda _{\max }}\left( {{{\bar H}^{\rm{T}}}\bar H} \right)\left\| {{{\bar u}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2, \end{array} $ |
即
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2} \right) \le h\left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 + \\ \left\| {{{\bar Z}_k}\left( { \cdot ,t - \tau } \right)} \right\|_{{{\rm{L}}^2}}^2 + g\left\| {{{\bar u}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2, \end{array} $ | (22) |
这里,h=λmax(AτTAτ)+1, g=λmax (HTH)。
在(22)式两端对t进行积分,可得:
| $ \begin{array}{l} \left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 \le \left\| {{{\bar Z}_k}\left( { \cdot ,0} \right)} \right\|_{{{\rm{L}}^2}}^2 + \int_0^t {h\left\| {{{\bar Z}_k}\left( { \cdot ,} \right.} \right.} \\ \left. {\left. s \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s + \int_0^t {g\left\| {{{\bar u}_k}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} + \int_0^t {h\left\| {{{\bar Z}_k}\left( { \cdot ,s - } \right.} \right.} \\ \left. {\left. \tau \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s。\end{array} $ | (23) |
将初值条件(9)式代入(23)式得:
| $ \begin{array}{l} \left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 \le \int_0^t {h\left\| {{{\bar Z}_k}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} + \\ \int_0^t {g\left\| {{{\bar u}_k}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} + \int_0^t {\left\| {{{\bar Z}_k}\left( { \cdot ,s - \tau } \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} , \end{array} $ | (24) |
下面对时滞项进行处理,注意Zk(x, t-τ)=[Zk1(x, t-τ1), Zk2(x, t-τ2), …, ZkN(x, t-τN)]T, 则
| $ \begin{array}{l} \int_0^t {\left\| {{{\bar Z}_k}\left( { \cdot ,s - \tau } \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} = \int_0^t {\left\| {\bar Z_k^1\left( { \cdot ,s - } \right.} \right.} \\ \left. {\left. {{\tau _1}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s + \int_0^t {\left\| {\bar Z_k^2\left( { \cdot ,s - {\tau _2}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} + \cdots + \\ \int_0^t {\left\| {\bar Z_k^N\left( { \cdot ,s - {\tau _N}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} = \sum\limits_{i = 1}^N {\int_0^t {\left\| {\bar Z_k^i\left( { \cdot ,s - } \right.} \right.} } \\ \left. {\left. {{\tau _i}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s, \end{array} $ | (25) |
对(25)式中,当i=1时,
| $ \begin{array}{l} \int_0^t {\left\| {\bar Z_k^1\left( { \cdot ,s - {\tau _1}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} = \int_0^t {\left\| {Z_{k + 1}^1\left( { \cdot ,s - {\tau _1}} \right) - } \right.} \\ \left. {Z_k^1\left( { \cdot ,s - {\tau _1}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s = \int_{ - {\tau _1}}^{t - {\tau _1}} {\left\| {Z_{k + 1}^1\left( { \cdot ,s} \right) - Z_k^1\left( { \cdot ,} \right.} \right.} \\ \left. {\left. s \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s, \end{array} $ | (26) |
若0≤t≤τ1时,根据初值条件(10),则式(26)有
| $ \begin{array}{l} \int_0^t {\left\| {\bar Z_k^1\left( { \cdot ,s - {\tau _1}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} = \int_{ - {\tau _1}}^{t - {\tau _1}} {\left\| {Z_{k + 1}^1\left( { \cdot ,s} \right) - } \right.} \\ \left. {Z_k^1\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s = 0。\end{array} $ | (27) |
若τ1≤t时,那么
| $ \begin{array}{l} \int_0^t {\left\| {\bar Z_k^1\left( { \cdot ,s - {\tau _1}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} = \int_{ - {\tau _1}}^{t - {\tau _1}} {\left\| {Z_{k + 1}^1\left( { \cdot ,s} \right) - } \right.} \\ \left. {Z_k^1\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s = \int_{ - {\tau _1}}^0 {\left\| {Z_{k + 1}^1\left( { \cdot ,s} \right) - Z_k^1\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} + \\ \int_0^{t - {\tau _1}} {\left\| {Z_{k + 1}^1\left( { \cdot ,s} \right) - Z_k^1\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} = \int_0^{t - {\tau _1}} {\left\| {Z_{k + 1}^1\left( { \cdot ,} \right.} \right.} \\ \left. {\left. s \right) - Z_{k + 1}^1\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s \le \int_0^t {\left\| {Z_{k + 1}^1\left( { \cdot ,s} \right) - Z_k^1\left( { \cdot ,} \right.} \right.} \\ \left. {\left. s \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s \le \int_0^t {\left\| {Z_k^1\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} , \end{array} $ | (28) |
因此,根据式(26)—(28),可得:
| $ \int_0^t {\left\| {\bar Z_k^1\left( { \cdot ,s - {\tau _1}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} \le \int_0^t {\left\| {\bar Z_k^1\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} , $ | (29) |
类似时滞项i=1的处理方法,i=2, 3, …, N也有类似的结果,所以
| $ \begin{array}{l} \int_0^t {\left\| {{{\bar Z}_k}\left( { \cdot ,s - \tau } \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} = \sum\limits_{i = 1}^N {\int_0^t {\left\| {\bar Z_k^i\left( { \cdot ,s - } \right.} \right.} } \\ \left. {\left. {{\tau _i}} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s \le \sum\limits_{i = 1}^N {\int_0^t {\left\| {\bar Z_k^i\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} } \le \\ \int_0^t {\left\| {{{\bar Z}_k}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} , \end{array} $ | (30) |
根据式(30)和式(24)中,那么
| $ \begin{array}{l} \left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 \le \int_0^t {a\left\| {{{\bar Z}_k}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} + \\ \int_0^t {g\left\| {{{\bar u}_k}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} , \end{array} $ | (31) |
这里a=h+1。
对式(31)利用Bellman-Gronwall引理得:
| $ \left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 \le g\int_0^t {{e^{a\left( {t - s} \right)}}\left\| {{{\bar u}_k}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s} , $ | (32) |
由式(8)开闭环P型迭代学习律可知,
| $ \begin{array}{l} \left\| {{{\bar u}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 \le 2{b_\Gamma }\left\| {{e_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 + \\ 2{b_l}\left\| {{e_{k + 1}}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2, \end{array} $ | (33) |
这里bΓ=
将式(33)带入式(32)可得如下:
| $ \begin{array}{l} \left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2 \le 2g\int_0^t {{e^{a\left( {t - s} \right)}}\left( {{b_\Gamma }\left\| {{e_k}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2 + } \right.} \\ \left. {{b_l}\left\| {{e_{k + 1}}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2} \right){\rm{d}}s, \end{array} $ | (34) |
令M1=max {2gbΓ, 2gbl},则(34)有
| $ \begin{array}{l} \left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2\int_0^t {{e^{a\left( {t - s} \right)}}\left( {{M_1}\left\| {{e_k}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2 + } \right.} \\ {M_1}\left\| {{e_{k + 1}}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{\rm{d}}s。\end{array} $ | (35) |
选择适当大的λ使得λ>a,并用e-λt乘以式(35)两边,可得到:
| $ \begin{array}{l} \left\| {{{\bar Z}_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}^2{e^{ - \lambda t}} \le {M_1}\int_0^t {{e^{ - \left( {\lambda - a} \right)\left( {t - s} \right)}}\left( {\left\| {{e_k}\left( { \cdot ,} \right.} \right.} \right.} \\ \left. {\left. {\left. s \right)} \right\|_{{{\rm{L}}^2}}^2{e^{ - \lambda s}} + \left\| {{e_{k + 1}}\left( { \cdot ,s} \right)} \right\|_{{{\rm{L}}^2}}^2{e^{ - \lambda s}}} \right){\rm{d}}s。\end{array} $ | (36) |
根据(L2, λ)范数的定义,式(36)两边取上确界变为
| $ \begin{array}{l} \left\| {{{\bar Z}_k}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2 \le \frac{{{M_1}}}{{\lambda - a}}\left\| {{e_k}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2 + \\ \frac{{{M_1}}}{{\lambda - a}}\left\| {{e_{k + 1}}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2, \end{array} $ | (37) |
在式(16)两边同乘e-λt(λ>a),然后两边同时取上确界得,
| $ \begin{array}{l} \left\| {{e_{k + 1}}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2 \le 2\rho \left\| {{e_k}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2 + \\ 2{b_c}\left\| {{{\bar Z}_k}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2。\end{array} $ | (38) |
将式(37)代入式(38)得:
| $ \begin{array}{l} \left\| {{e_{k + 1}}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2 \le 2\rho \left\| {{e_k}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2 + \\ \frac{{2{b_c}{M_1}}}{{\lambda - a}}\left\| {{e_k}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2 + \frac{{2{b_c}{M_1}}}{{\lambda - a}}\left\| {{e_{k + 1}}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2。\end{array} $ | (39) |
则,由式(39)有
| $ \left\| {{e_{k + 1}}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2 \le \frac{{2\rho + \frac{{2{b_c}{M_1}}}{{\lambda - a}}}}{{1 - \frac{{2{b_c}{M_1}}}{{\lambda - a}}}}\left\| {{e_k}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2, $ | (40) |
根据定理1的条件2ρ < 1知,则选取充分大的λ使得
| $ \mathop {\lim }\limits_{k \to \infty } \left\| {{e_k}} \right\|_{\left( {{{\rm{L}}^2},\lambda } \right)}^2 = 0,\forall t \in \left[ {0,T} \right]. $ | (41) |
由式(41)和(L2, λ)范数的定义易得:
| $ \mathop {\lim }\limits_{k \to \infty } {\left\| {{e_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}} = 0,\forall t \in \left[ {0,T} \right]. $ | (42) |
定理1证明结束。
若开闭环学习控制器的L(t)为零,则为开环学习控制器,误差收敛性有如下推论。
推论1 若定常被控学习系统(7)满足假设1~2,系统矩阵D≥0, 且开环学习控制器中的增益矩阵Γ(t)满足如下不等式:
| $ {\left\| {I - \bar G\Gamma \left( t \right)} \right\|^2} \le \rho ,2\rho \in \left[ {0,1} \right),\forall t \in \left[ {0,T} \right], $ | (43) |
则当迭代次数趋于无穷大时,系统输出误差的L2范数一致收敛到零,即
| $ \mathop {\lim }\limits_{k \to \infty } {\left\| {{e_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}} = 0,\forall t \in \left[ {0,T} \right]。$ |
证明 只需将开闭环控制器的闭环增益设定为零即可,其余过程类似定理1的证明。
2.2 时变系数的扩散耦合系统本小节将开闭环P型控制器拓展到时变的具扩散耦合系统(7),得到如下的定理。
定理2 若时变系数的学习系统(7)满足假设1~2,系统矩阵D(t)≥0,且开闭环学习控制器(8)中的增益矩阵Γ(t), L(t)满足如下不等式:
| $ \begin{array}{l} {\left\| {{{\left( {I + \bar G\left( t \right)L\left( t \right)} \right)}^{ - 1}}\left( {I + \bar G\left( t \right)\Gamma \left( t \right)} \right)} \right\|^2} \le \rho ,2\rho \in \\ \left[ {0,1} \right),\forall t \in \left[ {0,T} \right], \end{array} $ | (44) |
则当迭代次数趋于无穷大时,系统跟踪误差的L2范数一致收敛到零,即
| $ \mathop {\lim }\limits_{k \to \infty } {\left\| {{e_k}\left( { \cdot ,t} \right)} \right\|_{{{\rm{L}}^2}}} = 0,\forall t \in \left[ {0,T} \right]。$ |
证明 此证明过程类似定理1的证明,此处省略。
3 数值仿真选取如下的两个具扩散耦合的单输入单输出时滞偏微分系统:
| $ \left\{ \begin{array}{l} \frac{{\partial {Z^1}\left( {x,t} \right)}}{{\partial t}} = {A_\tau }{Z^1}\left( {x,t - {\tau _1}} \right) + B{\nabla ^2}{Z^1}\left( {x,t} \right) + \\ \;\;\;\;\;\;{D_{12}}{\nabla ^2}\left( {{Z^2}\left( {x,t} \right) - {Z^1}\left( {x,t} \right)} \right) + H{u^1}\left( {x,t} \right),\\ {y^1}\left( {x,t} \right) = C{Z^1}\left( {x,t} \right) + G{u^2}\left( {x,t} \right),\\ \frac{{\partial {Z^2}\left( {x,t} \right)}}{{\partial t}} = {A_\tau }{Z^2}\left( {x,t - {\tau _2}} \right) + B{\nabla ^2}{Z^2}\left( {x,t} \right) + \\ \;\;\;\;\;\;{D_{21}}{\nabla ^2}\left( {{Z^1}\left( {x,t} \right) - {Z^2}\left( {x,t} \right)} \right) + H{u^2}\left( {x,t} \right),\\ {y^2}\left( {x,t} \right) = C{Z^2}\left( {x,t} \right) + G{u^2}\left( {x,t} \right), \end{array} \right. $ |
其中(x, t)∈[0, 1]×[0, 1],
| $ \begin{array}{l} A = 0.6t,B = 0.6,{D_{21}} = {D_{12}} = 0.2,H = 0.8t,C = \\ 0.5{e^{ - 3t}},G = 1.2{e^{ - 1.9t}}, \end{array} $ |
时滞系数τ1=τ2=0.2。
令
| $ Z\left( {x,t - \tau } \right) = \left[ \begin{array}{l} {Z^1}\left( {x,t - {\tau _1}} \right)\\ {Z^2}\left( {x,t - {\tau _2}} \right) \end{array} \right], $ |
| $ u\left( {x,t} \right) = \left[ \begin{array}{l} {u^1}\left( {x,t} \right)\\ {u^2}\left( {x,t} \right) \end{array} \right],y\left( {x,t} \right) = \left[ \begin{array}{l} {y^1}\left( {x,t} \right)\\ {y^2}\left( {x,t} \right) \end{array} \right], $ |
则系统等价形式为
| $ \left\{ \begin{array}{l} \frac{{\partial Z\left( {x,t} \right)}}{{\partial t}} = {{\bar A}_z}Z\left( {x,t - \tau } \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\bar D{\nabla ^2}Z\left( {x,t} \right) + Hu\left( {x,t} \right),\\ y\left( {x,t} \right) = \bar CZ\left( {x,t} \right) + \bar Gu\left( {x,t} \right), \end{array} \right. $ |
式子系统矩阵为
| $ {{\bar A}_\tau } = \left[ {\begin{array}{*{20}{c}} {0.6t}&0\\ 0&{0.6t} \end{array}} \right],\bar D = \left[ {\begin{array}{*{20}{c}} {0.4}&{0.2}\\ {0.2}&{0.4} \end{array}} \right], $ |
| $ \bar C = \left[ {\begin{array}{*{20}{c}} {0.5{e^{ - 3t}}}&0\\ 0&{0.5{e^{ - 3t}}} \end{array}} \right], $ |
| $ \bar H = \left[ {\begin{array}{*{20}{c}} {0.8t}&0\\ 0&{0.8t} \end{array}} \right],\bar G = \left[ {\begin{array}{*{20}{c}} {1.2{e^{ - 1.9t}}}&0\\ 0&{1.2{e^{ - 1.9t}}} \end{array}} \right]。$ |
采取如下开闭环P型控制器及开环P型控制器:
| $ \begin{array}{l} {u_{k + 1}}\left( {x,t} \right) = {u_k}\left( {x,t} \right) + \Gamma \left( t \right){e_k}\left( {x,t} \right) + \\ L\left( t \right){e_{k + 1}}\left( {x,t} \right), \end{array} $ |
| $ {u_{k + 1}}\left( {x,t} \right) = {u_k}\left( {x,t} \right) + \Gamma \left( t \right){e_k}\left( {x,t} \right), $ |
其中
| $ \Gamma \left( t \right) = \left[ {\begin{array}{*{20}{c}} {1.2}&{0.01{e^{ - 1.5t}}}\\ 0&{1.19} \end{array}} \right], $ |
| $ L\left( t \right) = \left[ {\begin{array}{*{20}{c}} {0.9}&{0.03{e^{ - 2t}}}\\ 0&{1.15} \end{array}} \right]。$ |
给定期望跟踪轨迹为
| $ \begin{array}{l} {y_d}\left( {x,t} \right) = \left[ {\begin{array}{*{20}{c}} {y_d^1\left( {x,t} \right)}\\ {y_d^2\left( {x,t} \right)} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {3\left( {1 - {e^{ - 2t}}} \right)\sin \left( {3\pi x} \right)}\\ {4\sin \left( {6x} \right)\sin \left( {1.5\pi t} \right)} \end{array}} \right]。\end{array} $ |
通过以上的系统参数计算,可以得出下面的不等式:
| $ \begin{array}{l} {\left\| {{{\left( {I + \bar GL\left( t \right)} \right)}^{ - 1}}\left( {I + \bar G\Gamma \left( t \right)} \right)} \right\|^2} < 0.5,\\ {\left\| {I - \bar G\Gamma \left( t \right)} \right\|^2} < 0.5,\forall t \in \left[ {0,1} \right]。\end{array} $ |
上式两个不等式表明该仿真系统参数满足在开闭环P型学习律和开环P型学习律作用下系统跟踪误差的收敛性条件。
数值仿真步骤如下:首先,设定系统状态初边值条件为Z(x, 0)=0和Z(0, t)=Z(1, t)=0及第一次迭代控制输入u1(x, t)=0,将控制输入代到采用前向差分离散化后的系统状态方程中,得到当次的系统输出y1(x, t),然后算出当次的跟踪误差e1(x, t)=yd(x, t)-y1(x, t),进而把前一次的状态信息送入学习控制器中可计算出下次迭代的控制输入u2(x, t),如此循环往复,直到系统跟踪误差小于给定的精度值则停止迭代。
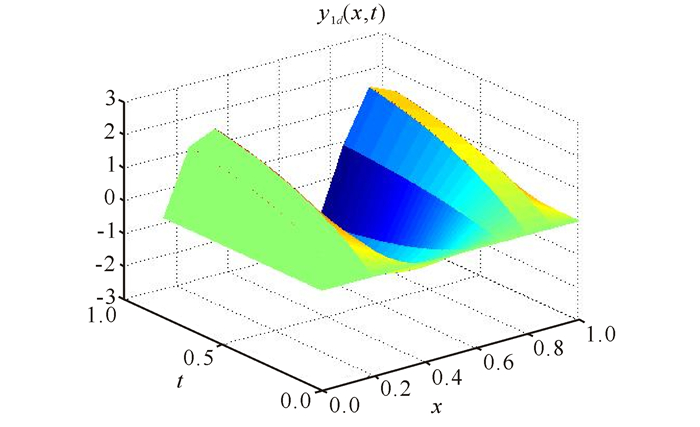
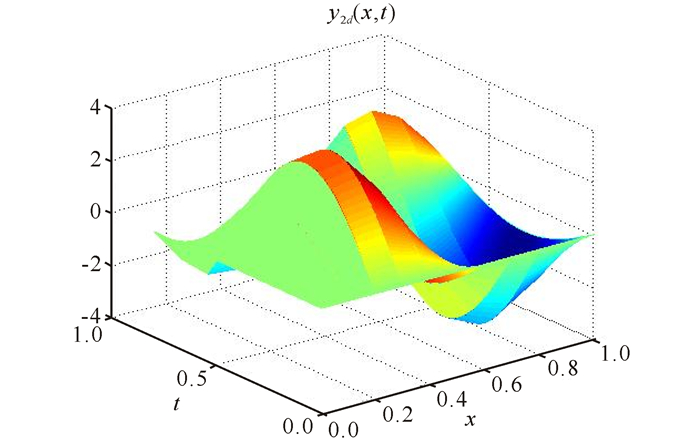
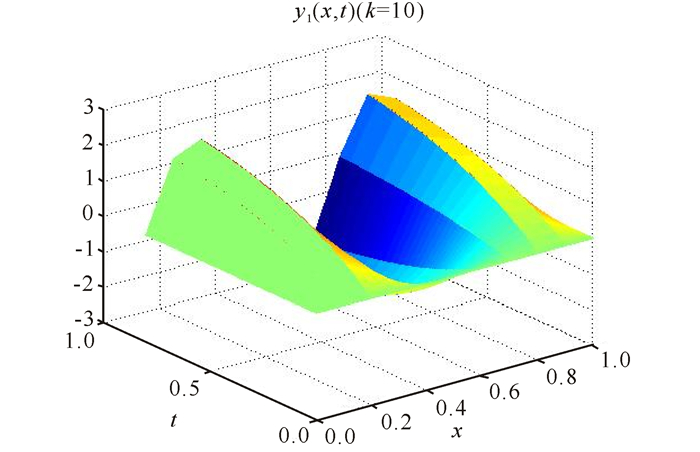
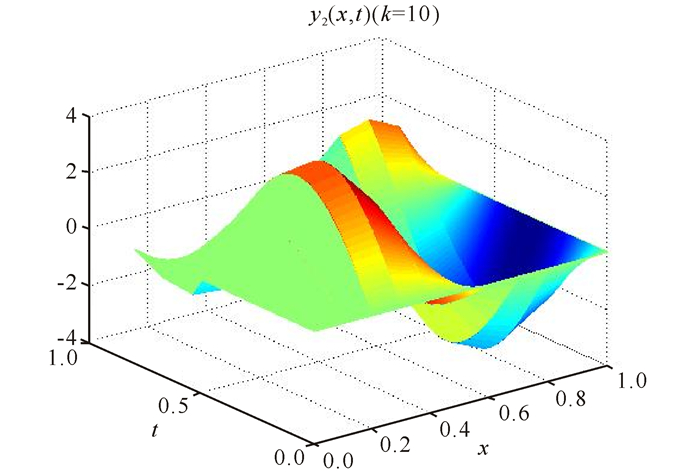
经过上述的仿真步骤,可得到如下的仿真图形,其中图 1~7为采用开闭环P型学习控制器的仿真结果。图 8为在开环P型迭代学习控制器作用下的结果。
|
图 1 期望曲面y1d(x, t) Fig.1 Desired surface y1d(x, t) |
|
图 2 期望曲面y2d(x, t) Fig.2 Desired surface y2d(x, t) |
|
图 3 实际跟踪曲面y1(x, t)(k=10) Fig.3 Actual tracking surface y1(x, t)(k=10) |
|
图 4 实际跟踪曲面y2(x, t)(k=10) Fig.4 Actual tracking surface y2(x, t)(k=10) |
|
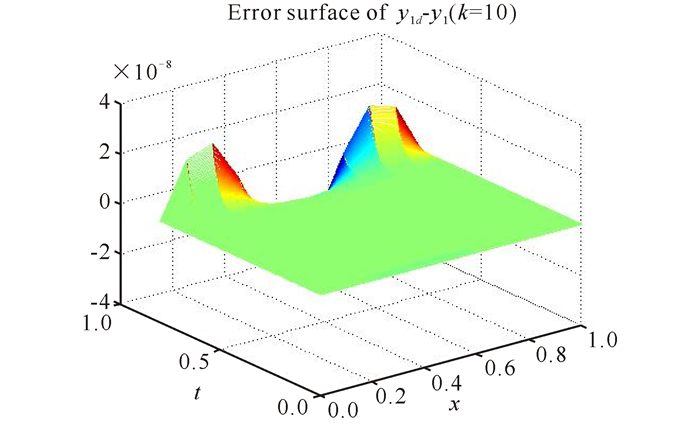
图 5 开闭环学习律下误差曲面y1d-y1(k=10) Fig.5 Error surface y1d-y1(k=10) under open-closed-loop learning law |
|
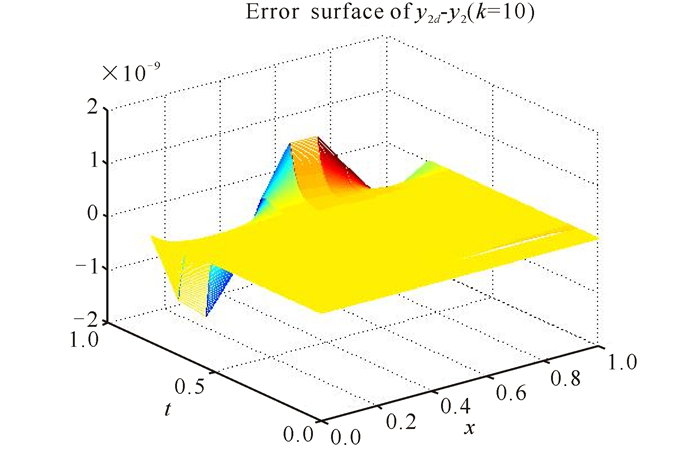
图 6 开闭环学习律下误差曲面y2d-y2(k=10) Fig.6 Error surface y2d-y2(k=10)under open-closed-loop learning law |
|
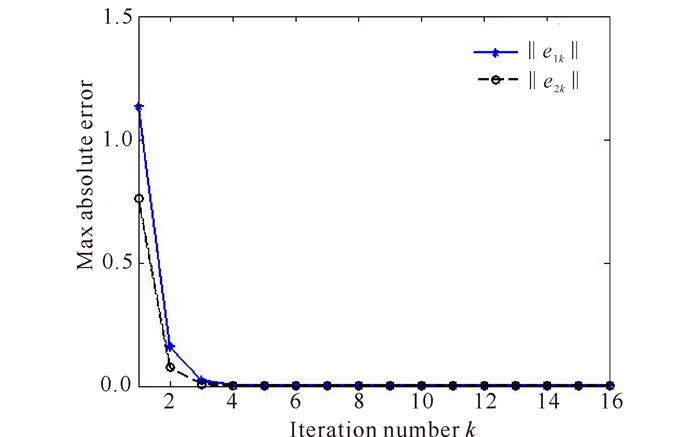
图 7 开闭环学习律下误差-迭代曲线 Fig.7 Error-iteration curve under open-closed-loop learning law |
|
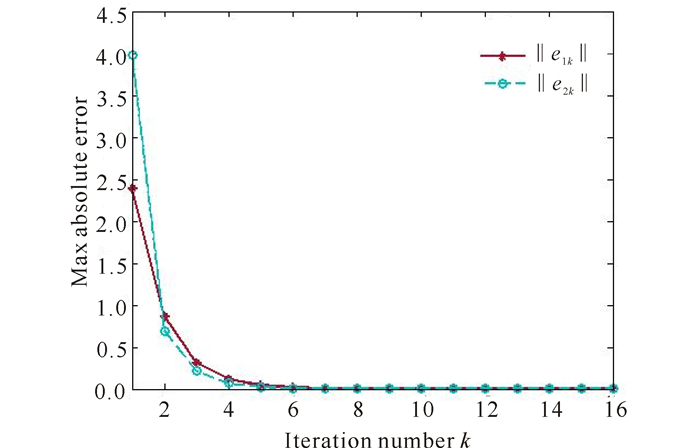
图 8 开环学习律下误差-迭代曲线 Fig.8 Error-iteration curve under open-loop learning law |
上面的仿真图中,图 1和图 2表示的是期望输出曲面y1d(x, t)和y2d(x, t),图 3和图 4表示的是迭代10次时实际输出曲面y1(x, t)(k=10)和y2(x, t)(k=10)。图 1~4表明迭代10次时的输出曲面已经和期望曲面十分相似。由图 5和图 6可以发现,在开闭环控制器作用下迭代10次时的最大跟踪误差分别为2.560 5×10-8和3.534 3×10-9。图 7和图 8分别描述了不同迭代次数下开闭环控制器和开环控制器作用下的最大误差曲线。图 7和图 8表明开闭环控制器的收敛速度相对于开环控制器要更快。该数值仿真表明,所提两种开闭环P型学习算法对具扩散耦合的偏微分系统跟踪控制是有效的。
4 结论本文研究了N个具有空间扩散耦合的偏微分时滞系统的轨迹跟踪问题,设计了开闭环P型迭代学习控制算法,并相应地给出了系统输出误差在L2范数意义下收敛的充分条件。同时,将定常学习系统的结论推广到了时变学习系统的情形。最后,通过两个具扩散耦合的偏微分时滞系统的数值仿真,验证了所给出结论的有效性。
| [1] |
LI H X, QI C K. Modeling of distributed parameter systems for applications-A synthesized review from time-space separation[J]. Journal of Process Control, 2010, 20(8): 891-901. DOI:10.1016/j.jprocont.2010.06.016 |
| [2] |
LI X Y, MAO W J. Finite-time stability and stabilisation of distributed parameter systems[J]. IET Control Theory & Applications, 2017, 11(5): 640-646. |
| [3] |
GAN Q T, XU R. Stability and hopf bifurcation of a delayed reaction-diffusion neural network[J]. Mathematical Methods in the Applied Sciences, 2011, 34(12): 1450-1459. DOI:10.1002/mma.v34.12 |
| [4] |
WU K N, ZHAO B X, YAO Y. Synchronization of coupled neutral-type delay partial differential systems[J]. Circuits, Systems & Signal Processing, 2016, 35(2): 443-458. |
| [5] |
WU K N, CHEN B S. Synchronization of partial differential systems via diffusion coupling[J]. IEEE Transactions on Circuits and Systems Ⅰ:Regular Papers, 2012, 59(11): 2655-2668. DOI:10.1109/TCSI.2012.2190670 |
| [6] |
WANG J L, WU H N, HUANG T, et al. Pinning control strategies for synchronization of linearly coupled neural networks with reaction-diffusion terms[J]. IEEE Trans Neural Netw Learn Syst, 2016, 27(4): 749-761. DOI:10.1109/TNNLS.2015.2423853 |
| [7] |
孙明轩, 黄宝健. 迭代学习控制[M]. 北京: 国防工业出版社, 1999. SUN M X, HUANG B J. Iterative learning control[M]. Beijing: National Defence Industrial Press, 1999. |
| [8] |
谢胜利, 田森平, 谢振东. 迭代学习控制的理论与应用[M]. 北京: 科学出版社, 2005. XIE S L, TIAN S P, XIE Z D. Theory and application of iterative learning control[M]. Beijing: Science Press, 2005. |
| [9] |
CHI R H, HOU Z S, JIN S T, et al. A data-driven iterative feedback tuning approach of alinea for freeway traffic ramp metering with paramics simulations[J]. IEEE Transactions on Industrial Informatics, 2013, 9(4): 2310-2317. DOI:10.1109/TII.2013.2238548 |
| [10] |
LUO B, WU H N, LI H X. Adaptive optimal control of highly dissipative nonlinear spatially distributed processes with neuro-dynamic programming[J]. IEEE Trans Neural Netw Learn Syst, 2015, 26(4): 684-696. DOI:10.1109/TNNLS.2014.2320744 |
| [11] |
WANG Y Q, ZHOU D H, GAO F R. Iterative learning model predictive control for multi-phase batch processes[J]. Journal of Process Control, 2008, 18(6): 543-557. DOI:10.1016/j.jprocont.2007.10.014 |
| [12] |
CHOI J, SEO B J, LEE K S. Constrained digital regulation of hyperbolic PDE systems:A learning control approach[J]. Korean Journal of Chemical Engineering, 2001, 18(5): 606-611. DOI:10.1007/BF02706375 |
| [13] |
CICHY B, GALKOWSKI K, ROGERS E. Iterative learning control for spatio-temporal dynamics using crank-nicholson discretization[J]. Multidimensional Systems and Signal Processing, 2012, 23(1): 185-208. |
| [14] |
XIAO T F, LI H X. Eigenspectrum-based iterative learning control for a class of distributed parameter system[J]. IEEE Transactions On Automatic Control, 2016, 62(1): 834-836. |
| [15] |
HUANG D Q, XU J X, LI X F, et al. D-type anticipatory iterative learning control for a class of inhomogeneous heat equations[J]. Automatica, 2013, 49(8): 2397-2408. DOI:10.1016/j.automatica.2013.05.005 |
| [16] |
HUANG D Q, LI X F, XU J X, et al. Iterative learning control of inhomogeneous distributed parameter systems-frequency domain design and analysis[J]. Systems & Control Letters, 2014, 72: 22-29. |
| [17] |
DAI X S, XU C, TIAN S P, et al. Iterative learning control for MIMO second-order hyperbolic distributed parameter systems with uncertainties[J]. Advances in Difference Equations, 2016(1): 94. |
| [18] |
DAI X S, TIAN S P, PENG Y J, et al. Closed-loop P-type iterative learning control of uncertain linear distributed parameter systems[J]. IEEE/CAA Journal of Automatica Sinica, 2014, 1(3): 267-273. DOI:10.1109/JAS.2014.7004684 |
| [19] |
FU Q, GU P P, WU J R. Iterative learning control for one-dimensional fourth order distributed parameter systems[J]. Science China:Information Sciences, 2017, 60(1): 012204. DOI:10.1007/s11432-015-1031-6 |
| [20] |
HUANG D Q, XU J X. Steady-state iterative learning control for a class of nonlinear PDE processes[J]. Journal of Process Control, 2011, 21(8): 1155-1163. DOI:10.1016/j.jprocont.2011.06.018 |
| [21] |
HE W, HUANG T T, HUANG D Q, et al. Adaptive boundary iterative learning control for an Euler-Bernoulli beam system with input constraint[J]. IEEE Trans Neural Netw Learn Syst, 2017(99): 1-11. |
| [22] |
LI J M, ZHANG W Y, CHEN M L. Synchronization of delayed reaction-diffusion neural networks via an adaptive learning control approach[J]. Computers and Mathematics with Applications, 2013, 65: 1775-1785. DOI:10.1016/j.camwa.2013.03.016 |
| [23] |
CHEN W H, LI D X, LU X M. Impulsive observers with variable update intervals for Lipschitz nonlinear time-delay systems[J]. International Journal of Systems Science, 2013, 44(10): 1934-1947. DOI:10.1080/00207721.2012.670305 |
| [24] |
CHEN W H, GUAN Z H, LU X M. Guaranteed cost control for uncertain discrete-time Markovian jump systems with mode-dependent time-delays[J]. Control Theory & Applications, 2004, 21(4): 2270-2277. |
 2017, Vol. 24
2017, Vol. 24 


