0 引言

【研究意义】在鸟群的列队飞行、鱼群的聚集游动、昆虫和微生物的集体觅食等自然现象中，生物常常会表现出每个个体不具备的宏观、有序的群体智能行为。受此启发，科学家把具有一定自主能力的实体定义为智能体，而智能体之间通过信息传递进行交互作用，实现单个智能体所不能完成的各种艰巨、复杂、精度要求高的任务。但是，由于通信网络的不确定，使得在信息交换中出现了大量的信息延迟和丢失现象，导致多智能体系统协同问题变得复杂，因此有必要开展相关的研究。【前人研究进展】多智能体系统的一致性跟踪主要是通过智能体与其邻居或领航者之间进行信息交换，并按照设计的分布式一致性跟踪算法进行数据处理，使得所有智能体的状态能够跟踪领航者的实时动态^[1-7]。Ren等^[8]通过把参考输入信号看成虚拟的领航者，并基于参考输入分别为定常信号和时变信号，给出能够使多智能体系统达到跟踪目标的连续跟踪算法。Xie等^[9]研究具有虚拟领航者和通信时延的二阶多智能体一致性跟踪问题。考虑在离散时间多智能体系统中，智能体之间存在通信带宽、能量约束和不可靠通信信道等问题的影响，因此Ren等^[10-11]还研究了一阶多智能体系统的采样信号协调跟踪问题，并提出一种类似比例-微分(PI-like)的跟踪算法，用于跟踪具有时变时延的参考输入信号。实际上，多智能体系统中存在两类时延：智能体之间信息传输存在的随机时延称为通信时延；智能体本身存在的多个局部信息采集与计算导致的随机时延统称为输入时延。这两类时延的存在，导致很多不充分考虑时延的研究成果^[12-15]保守性较大。Cui等^[16], Ni等^[17]和Xiao等^[18]进而研究了具有通信时变时延的离散时间多智能体系统的一致性问题。Tian等^[19]利用频域分析方法研究了同时具有通信时变时延和输入时延的离散时间多智能体系统的一致性问题，并得出系统一致性条件仅与输入时延有关，而与通信时延无关的结论。【本研究切入点】 针对同时存在通信时变时延和输入时变时延的一阶离散时间多智能体系统，设计具有较小保守性的一致性跟踪协议，得到了该多智能体系统满足渐近一致性跟踪的充分条件。【拟解决的关键问题】证明具有两类时变时延的多智能体系统建模和渐近一致性跟踪充分条件，进而得到保守性更小的一致性跟踪条件。

1 多智能体系统建模

采用图论知识来简洁描述智能体之间信息交换的过程。令G={V, E, A}表示一个加权有向图，其中V={v₁, …, v_N}表示图G是由N个节点组成的集合，E⊆V×V表示图G的边集合，所有节点的下标集合可以表示为Ι={1, 2, …, N}，图G的邻接矩阵为A={a_ij}∈$\mathfrak{R}$^N×N，其中矩阵元素a_ij为节点v_i与节点v_j之间的连接权重，当v_i可以获得v_j的信息时，取a_ij>0，否则a_ij=0，若节点v_i自身有反馈跟踪控制律时，则取a_ii>0，否则a_ii=0。定义节点v_i的邻居集合为N_i={v_j∈V:(v_i, v_j)∈E}。

考虑一阶离散时间多智能体系统模型:

$ {x_i}\left( {k + 1} \right) = {x_i}\left( k \right) + {u_i}\left( k \right),\;\;\;\;i \in I。$

(1)

这里x_i∈$\mathfrak{R}$和u_i∈$\mathfrak{R}$分别为多智能体i的状态和输入控制信号。在研究中采用的离散跟踪控制律为

$ {u_i}\left( k \right) = - {a_{ii}}\left( {{x_i}\left( k \right) - a\left( k \right)} \right) + \sum\limits_{{v_j} \in {N_i}} {{a_{ij}}\left( {{x_j}\left( k \right) - {x_i}\left( k \right)} \right)} 。$

(2)

这里，N_i表示智能体i的邻居节点集合，a_ij>0是有向图G={V, E, A}的邻接矩阵A的矩阵元素，a_ii>0为控制增益，α(k)表示时变跟踪信号，当α(k)=α时，则为定常跟踪信号。

假定智能体i存在输入时延T_ii，则系统(1)可改写为

$ {x_i}\left( {k + 1} \right) = {x_i}\left( k \right) + {u_i}\left( {k - {T_{ii}}} \right),\;\;\;i \in I。$

(3)

令智能体本身的输入时延与智能体之间的通信时延之和为T_ij，则具有时延的一致性跟踪算法为

$ \begin{array}{l} {u_i}\left( {k - {T_{ii}}} \right) = - {a_{ii}}\left( {{x_i}\left( {k - {T_{ii}}} \right) - a\left( k \right)} \right) + \\ \sum\limits_{{v_j} \in {N_i}} {{a_{ij}}\left( {{x_j}\left( {k - {T_{ii}}} \right) - {x_i}\left( {k - {T_{ii}}} \right)} \right)} 。\end{array} $

因为T_ii≤T_ij，为便于处理，在跟踪算法的一致性项用中用x_i(k-T_ij)替换x_i(k-T_ii)，则上式可改写为

$ \begin{array}{l} {u_i}\left( k \right) = - {a_{ii}}\left( {{x_i}\left( {k - {T_{ii}}} \right) - \alpha \left( k \right)} \right) + \\ \sum\limits_{{v_j} \in {N_i}} {{a_{ij}}\left( {{x_j}\left( {k - {T_{ij}}} \right) - {x_i}\left( {k - {T_{ij}}} \right)} \right)} 。\end{array} $

(4)

令两类时变时延分别表示为T_ii=(m-1)T+ε₁，T_ij=(n-1)T+ε₂，式中T为采样周期, T_ii>0, T_ij>0。变量m和n均为非负整数, ε₁, ε₂∈(0, T)。则T_ii, T_ij可以近似转化为采样周期的整数倍，即T_ii=mT，T_ij=nT.这里，m≤n。因此，(4)式的闭环系统可以写为

$ \begin{array}{l} {x_i}\left( {k + 1} \right) = {x_i}\left( k \right) - {a_{ii}}\left[ {{x_i}\left( {k - m} \right) - \alpha \left( k \right)} \right] + \\ \sum\limits_{{v_j} \in {N_i}} {{a_{ij}}\left[ {{x_j}\left( {k - n} \right) - {x_i}\left( {k - n} \right)} \right]} ,\;\;\;i \in I。\end{array} $

(5)

为方便设计分布式一致性跟踪算法，介绍如下引理。

引理1 (圆盘定理)^[20]  设A=(a_ij)为任一N阶复数矩阵, 则A的特征值都在复数平面上的N个圆盘

$ \left| {z - {a_{ii}}} \right| \le {R_i},\left( {i = 1,2, \cdots ,N} \right) $

的并集内。这里的R_i=|a_i1|+|a_i2|+…+|a_{i, i-1}|+|a_{i, i+1}|+…+|a_iN|。

引理2^[19]  以下不等式：

$ \frac{{\sin \left( {\frac{{2D + 1}}{2}\omega } \right)}}{{\sin \left( {\frac{\omega }{2}} \right)}} \le 2D + 1, $

在D为非负整数和ω∈[-π, π]时成立。

2 具有通信和输入时延的一致性跟踪算法

利用频域分析方法和矩阵理论，得到具有两类时延的多智能体系统(5)渐近一致的充分条件。

定理1  假设由N个智能体组成的多智能体系统(5)，系统通信拓扑G={V, E, A}为有向连通图，如果满足充分条件:

$ {K_{ii}}\left( {2m + 1} \right) + {K_{ij}}\left( {2n + 1} \right) < 2, $

其中，K_ii=a_ii为智能体i的反馈增益，${K_{ij}} = \sum\limits_{{v_j} \in {N_i}} {{a_{ij}}} $为智能体i的邻接加权和，则该多智能体系统能够实现渐近一致性跟踪。

证明  对(5)式进行z变换，可以得到:

$ \begin{array}{l} z{X_i}\left( z \right) = {X_i}\left( z \right) - {a_{ii}}\left[ {{z^{ - m}}{X_i}\left( z \right) - \alpha \left( z \right)} \right] + \\ \sum\limits_{{v_j} \in {N_i}} {{a_{ij}}\left[ {{z^{ - n}}{X_j}\left( z \right) - {z^{ - n}}{X_i}\left( z \right)} \right]} , \end{array} $

(6)

其中，X_i(z)和α(z)分别是x_i(k)和α(k)的z变换形式。定义一个N维的正定矩阵$\tilde L\left( z \right) = \left\{ {{{\tilde l}_{ij}}\left( z \right)} \right\}$如下：

$ {{\tilde l}_{ij}}\left( z \right) = \left\{ \begin{array}{l} - {a_{ij}}{z^{ - n}},{v_j} \in {N_i};\\ {a_{ii}}{z^{ - m}} + \sum\limits_{{v_j} \in {N_i}} {{a_{ij}}{z^{ - n}}} ,i = j;\\ 0,{\rm{others}}{\rm{。}} \end{array} \right. $

令X(z)=[X₁(z), …, X_N(z)]^T，Q=diag(a₁₁, …, a_NN)。那么(6)式可以写成增广矩阵的形式:

$ zX\left( z \right) = X\left( z \right) + Q\alpha \left( z \right) - \tilde L\left( z \right)X\left( z \right), $

以α(z)为输入，X(z)为输出，则系统(6)的闭环特征方程为$p\left( z \right) = \det \left[{I + \left( {1/\left( {z-1} \right)} \right)\tilde L\left( z \right)} \right]$。根据稳定性定理，若能证明p(z)=0的所有特征根的模均小于1，则该系统能够达到渐近一致。

由广义奈奎斯特稳定判据知，对于ω∈[-π, π]，当(1/(e^jω-1))${\tilde L}$(e^jω)的所有极点λ((1/(e^jω-1))${\tilde L}$(e^jω))不包含点(-1, j0)时，p(z)=0所有根的模均小于1。而根据引理1，λ((1/(e^jω-1))${\tilde L}$(e^jω))在以下N个圆盘的并集内：

$ \begin{array}{l} {D_i} = \\ \left\{ {\left| {\xi - \frac{{{a_{ii}}{e^{ - j\omega m}} + \sum\limits_{{v_j} \in {N_i}} {{a_{ij}}{e^{ - j\omega n}}} }}{{{e^{j\omega }} - 1}}} \right| \le \sum\limits_{{v_j} \in {N_i}} {\left| {\frac{{{a_{ij}}{e^{ - j\omega n}}}}{{{e^{j\omega }} - 1}}} \right|} } \right\}。\end{array} $

令K_ii=a_ii, ${K_{ij}} = \sum\limits_{{v_j} \in {N_i}} {{a_{ij}}} $。定义

$ {G_i}\left( \omega \right) = \frac{{{K_{ii}}{e^{ - j\omega n}} + {K_{ij}}{e^{ - j\omega n}}}}{{{e^{j\omega }} - 1}}。$

容易看出，G_i(ω)是圆盘D_i的中心。那么对于ω∈[-π, π]，当a≥1时，点(-a, j0)不在圆盘D_i内。因此，当ω∈[-π, π], a≥1时，以下不等式成立:

$ \left| { - a + j0 - \frac{{{K_{ii}}{e^{ - j\omega n}} + {K_{ij}}{e^{ - j\omega n}}}}{{{e^{j\omega }} - 1}}} \right| > \left| {\frac{{{K_{ij}}{e^{ - j\omega n}}}}{{{e^{j\omega }} - 1}}} \right|。$

根据以上不等式可以得到:

$ \begin{array}{l} f\left( a \right) = {\left| { - a + j0 - \frac{{{K_{ii}}{e^{ - j\omega n}} + {K_{ij}}{e^{ - j\omega n}}}}{{{e^{j\omega }} - 1}}} \right|^2} - \\ {\left| {\frac{{{K_{ij}}{e^{ - j\omega n}}}}{{{e^{j\omega }} - 1}}} \right|^2} = \left\{ {4{{\sin }^2}\left( {\frac{\omega }{2}} \right){a^2} - } \right.\\ 4\left[ {{K_{ii}}\sin \left( {\frac{\omega }{2}} \right)\sin \left( {\frac{{2m + 1}}{2}\omega } \right) + } \right.\\ \left. {{K_{ij}}\sin \left( {\frac{\omega }{2}} \right)\sin \left( {\frac{{2n + 1}}{2}\omega } \right)} \right]a + K_{ii}^2 + \\ \left. {2{K_{ii}}{K_{ij}}\cos \left[ {\left( {n - m} \right)\omega } \right]} \right\}/4{\sin ^2}\left( {\frac{\omega }{2}} \right) > 0。\end{array} $

容易看出，f(a)是一个一元二次函数，其开口朝上。

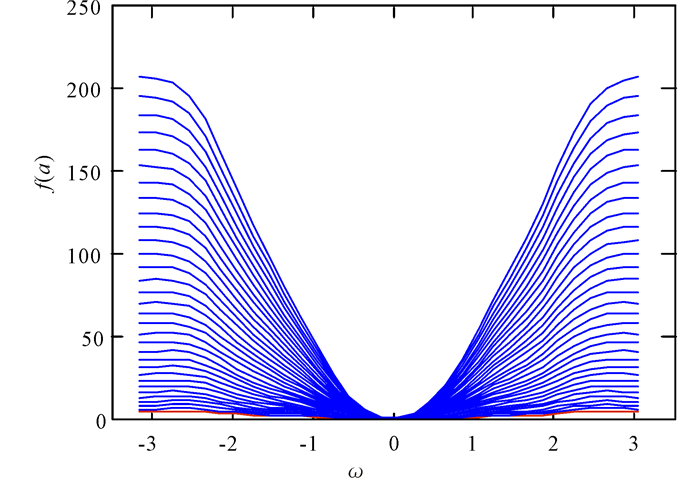
为了说明f(a)和ω∈[-π, π]之间的对应关系，令m=1, n=4，K_ii=0.1, K_ij=0.15, 且ω的步长为0.2时，则两者的函数关系如图 1所示。

当|ω|较小时，f(a)的值较小，反之则相应值较大；同时f(1)时为该曲线族底部，即当a≥1时，f(a)>0，则f(1)>0。选择f^′(1)>0，则有如下条件：

$ \begin{array}{l} f'\left( 1 \right) = \\ \frac{{8{{\sin }^2}\left( {\frac{\omega }{2}} \right) - 4\left[ {{K_{ii}}\sin \left( {\frac{\omega }{2}} \right)\sin \left( {\frac{{2m + 1}}{2}\omega } \right) + {K_{ij}}\sin \left( {\frac{\omega }{2}} \right)\sin \left( {\frac{{2n + 1}}{2}\omega } \right)} \right]}}{{4{{\sin }^2}\left( {\frac{\omega }{2}} \right)}} = \\ 2 - {K_{ii}}\frac{{\sin \left( {\frac{{2m + 1}}{2}\omega } \right)}}{{\sin \left( {\frac{\omega }{2}} \right)}} - {K_{ij}}\frac{{\sin \left( {\frac{{2n + 1}}{2}\omega } \right)}}{{\sin \left( {\frac{\omega }{2}} \right)}} \end{array} $

根据引理2，可以得到$\sin \left( {\frac{{2m + 1}}{2}\omega } \right)/\sin \left( {\frac{\omega }{2}} \right) \le 2m + 1$，$\sin \left( {\frac{{2n + 1}}{2}\omega } \right)/\sin \left( {\frac{\omega }{2}} \right) \le 2n + 1$。当ω∈[-π, π]时成立，那么有

$ \begin{array}{l} \frac{{{K_{ii}}\sin \left( {\frac{{2m + 1}}{2}\omega } \right) + {K_{ij}}\sin \left( {\frac{{2n + 1}}{2}\omega } \right)}}{{\sin \left( {\frac{\omega }{2}} \right)}} \le \\ {K_{ii}}\left( {2m + 1} \right) + {K_{ij}}\left( {2n + 1} \right) < 2。\end{array} $

即如果满足此条件约束，多智能体系统(5)能够实现渐近一致跟踪。

注意1  定理1同样适用于仅具有单时变时延的情况，令m=0，则仅考虑通信时延，令m=n，则仅考虑输入时延，令n=m=0，则不考虑时延。

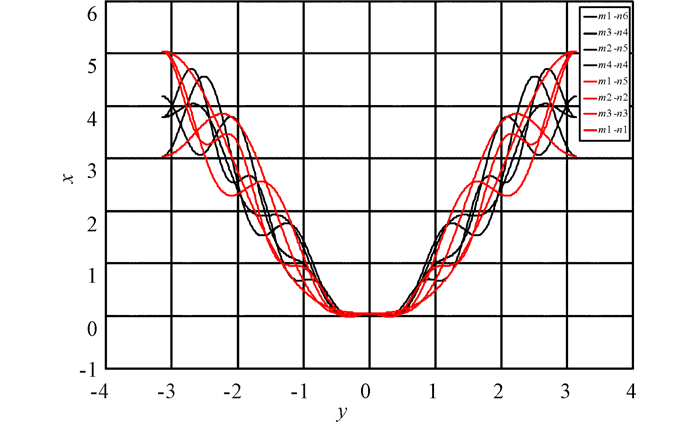
考虑到定理1是在假设f(1)>0, f^′(1)>0同时成立的条件下，仅根据f^′(1)>0得到的不等式条件。实际上，由于ω∈[-π, π]的影响，特别是在输入时延和通信时延m, n较大的时候，会出现在f^′(1)>0的情况下，ω∈(0 1)中的少部分值使得f(1) < 0，具体情况如图 2所示。这里m1-n6表示输入时延为m=1，输入与网络通信综合时延为n=6。

由图 2知，在满足定理1条件的前提下，部分满足f(1) < 0条件的多智能体仍然能够达到渐近一致性跟踪，如第5、第7条函数曲线。只有当f(1)的最小值小于一定的界限，多智能体系统跟踪曲线才会发散。

所以针对定理1，有如下推论。

推论1  假设由N个智能体组成的体系统(5)，通信拓扑G={V, E, A}为有向连通图，如果满足充分条件:

$ \left\{ \begin{array}{l} 4{\sin ^2}\left( {\frac{\omega }{2}} \right) - 4\left[ {{K_{ii}}\sin \left( {\frac{\omega }{2}} \right)\sin \left( {\frac{{2m + 1}}{2}\omega } \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {{K_{ij}}\sin \left( {\frac{\omega }{2}} \right)\sin \left( {\frac{{2n + 1}}{2}\omega } \right)} \right] + \\ \;\;\;\;\;\;\;\;K_{ii}^2 + 2{K_{ii}}{K_{ij}}\cos \left[ {\left( {n - m} \right)\omega } \right] > - \xi ,\\ {K_{ii}}\left( {2m + 1} \right) + {K_{ij}}\left( {2n + 1} \right) < 2。\end{array} \right. $

其中，ζ∈$\mathfrak{R}$⁺, ω∈[-π, π], m≤n。其他符号与定理1相同, 则系统(5)的能够实现渐近一致跟踪。

3 仿真实例

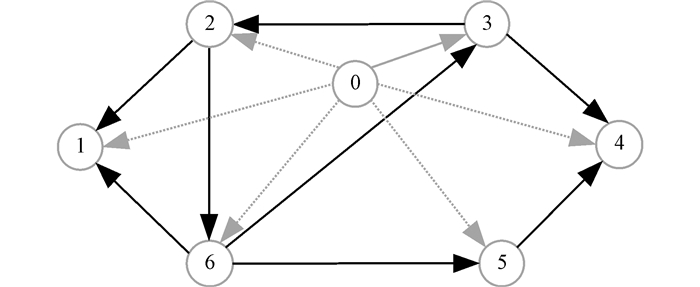
例  考虑由6个智能体组成的多智能体系统，其信息交换拓扑如图 3所示。各权值系数分别为a₁₁=a₂₂=…=a₆₆=0.1, a₁₂=0.1, a₁₆=0.05, a₂₃=0.15, a₃₆=0.1, a₄₃=0.05, a₄₅=0.1, a₅₆=0.15, a₆₂=0.15。节点0为跟踪信号，对应的虚线连接表示与其连接的智能体能够收到跟踪信号。各智能体的初始状态设为x(0)=(8, 6, 5, 3, 0, -2)^T。

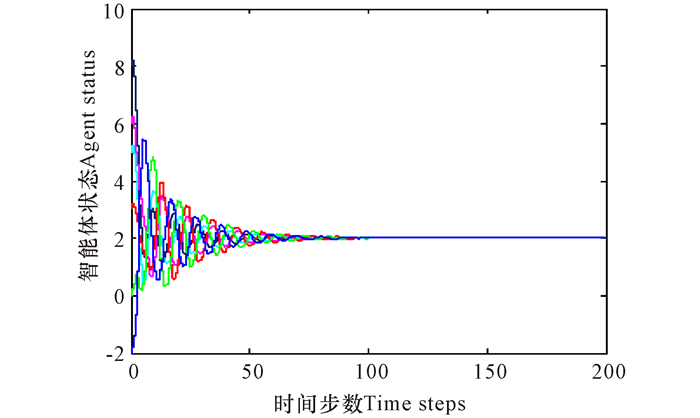
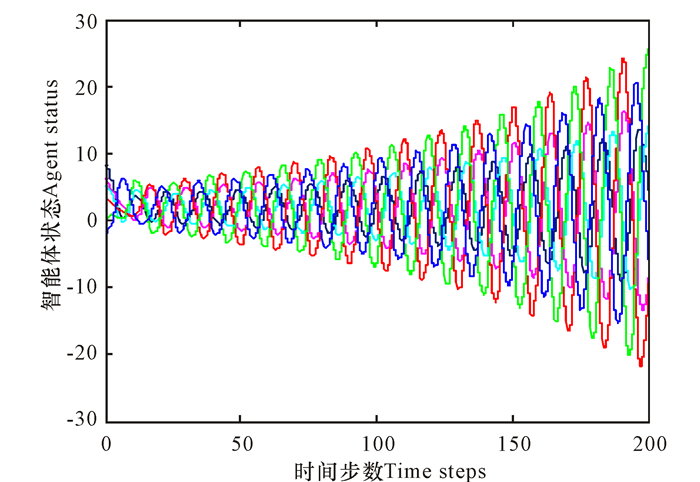
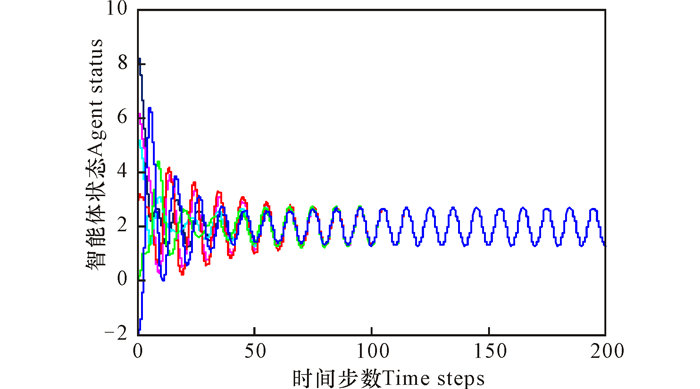
当定常参考信号α(k)=2和时变参考信号α(k)=sin (k)+2时，首先考虑所有智能体均能收到跟踪信号，其仿真结果如图 4~6所示。仿真表明，在满足定理1的条件下，系统的一致性跟踪问题能得到很好的解决；同时根据推论1，得到在这种情形下的最小界限值为ζ=0.0056。图 5显示，在不满足定理1的条件下，系统是发散的，不能做到渐近一致跟踪。

4 结论

在多智能体系统同时存在时变通信时延与输入时延的情况下，推导出使得该系统达到渐近一致性跟踪的充分条件，为有效解决一阶离散多智能体系统的定常跟踪和时变跟踪问题提供一种可行性方法。与常规的一致性跟踪协议相比，本研究所提出的协议中没有将输入时延做简化处理，从而减少了系统的保守性。同时也得出了多智能体一致性跟踪问题不仅与通信时延有关，也与输入时延有关的结论。仿真结果表明，只要选择合适的参数，多智能体系统便可以很好地实现对定常或时变参考信号的一致性跟踪。