【研究意义】研发使用高效率太阳电池是解决能源危机和环境污染的一个有效方式,现成为当今国际研究的热点之一[1-2]。目前用于制作太阳电池的Si、Ge、GaAs等常规材料都不能完全覆盖太阳光谱,从而制约了太阳电池的发展。第三代半导体GaN及其系列材料(包括InN、GaN、AlN及其合金)的出现,使太阳电池效率的进一步提高成为可能[3]。尤其是直接带隙半导体材料InGaN,可以通过改变In组分,实现带隙宽度从0.7 eV (InN)到3.4 eV (GaN)连续可调[4-5],所对应的吸收光谱的波长大约为365~1 770 nm,从紫外波段一直延伸到红外波段,几乎覆盖整个太阳光谱,因此它能够很好地吸收在太阳光谱范围内的各个频率的光子,从而转化为电能,为高效的光电转换提供了材料基础。另外,InGaN的吸收系数较高(约105 cm-1)[6],几百纳米的InGaN层即可吸收极大部分入射光,相比之下,硅却至少需要几百个微米厚,侧面表明InGaN是一种节约资源的材料;而且,InGaN还具有电子和空穴的有效质量低、电子迁移率高、饱和速度快[7]等一系列优点,是制备多结电池等复杂器件所需的重要性质;除此之外,InGaN材料的化学稳定性、机械强度、耐高温、耐腐蚀性能都十分优越,还具有抗辐射性能,可以在恶劣环境甚至在太空中工作,潜力巨大,可制备成空间太阳电池[8]。因此,InGaN材料在制备高效低成本太阳电池方面具有诸多潜力,从而成为人们研究的热点课题之一。【前人研究进展】很多研究小组在过去几年里制备或模拟了多种结构的太阳电池器件[9],但是实际转换效率并不理想,普遍在1%~3%[10-13]。Yang等[14]制备并分析了低In组分的InGaN单结太阳电池,但并没有对全太阳光谱下电池的工作特性进行研究。Zhang等[15]优化了In0.65Ga0.35N单结太阳电池, 但对于太阳电池中的杂质和缺陷没有进行详细讨论。周梅等[16]模拟并分析了p-InGaN层厚度对p-i-n结构InGaN太阳电池性能的影响和机理,指出选择较薄的p-InGaN层有利于提高p-i-n结构InGaN太阳电池的效率。文博等[17]通过计算证明了将InGaN材料分别应用于单结、双结和三结太阳电池中,电池的转换效率皆有很大提高,并计算得到了InxGa1-xN单、双和三结太阳电池的最佳禁带宽度和组分。【本研究切入点】由于高In组分InGaN材料的生长较为困难,故本研究借助计算机软件从理论上对InGaN太阳电池进行模拟和计算,研究各个参数对电池性能的影响,为制备高效太阳电池提供理论基础。【拟解决的关键问题】本研究采用AMPS-1D软件,从理论上根据解连续性方程以及泊松方程模拟计算InGaN/Si异质单结太阳电池器件的光电转换性能随p-Si衬底掺杂浓度变化的规律,并分析其物理机制。
1 材料与方法 1.1 软件介绍本模拟计算运用了太阳电池模拟软件AMPS-1D,全称是Analysis of Microelectronic and Photonic Structures-One Dimensional,即一维光电子和微电子器件结构分析模拟软件[18]。AMPS-1D模拟分析的基本原理方程有3个:泊松方程、电子连续性方程和空穴连续性方程[19]。泊松方程的计算公式如下:
| $ \begin{array}{l} \frac{{\rm{d}}}{{{\rm{d}}x}}\left[{\varepsilon \left( x \right)\frac{{{\rm{d}}\psi \left( x \right)}}{{{\rm{d}}x}}} \right] = q\left[{p\left( x \right)-n\left( x \right) + N_D^ + \left( x \right)-} \right.\\ \left. {N_A^-\left( x \right) + {p_t}\left( x \right) - {n_t}\left( x \right)} \right], \end{array} $ | (1) |
式中,ε为介电常数,ψ为静电势,n(x)、p(x)为电子和空穴浓度,nt(x)、pt(x)为复合中心电子和空穴的浓度。
电子连续性方程计算公式如下:
| $ \frac{1}{q}\left[{\frac{{{\rm{d}}{J_n}\left( x \right)}}{{{\rm{d}}x}}} \right] = -{G_L}\left( x \right) + R\left( x \right)。$ | (2) |
空穴连续性方程计算公式如下:
| $ \frac{1}{q}\left[{\frac{{{\rm{d}}{J_p}\left( x \right)}}{{{\rm{d}}x}}} \right] = {G_L}\left( x \right) -R\left( x \right)。$ | (3) |
式2)和式3)中,
AMPS-1D输入界面有两个计算模式:DOS model和Lifetime model,为了计算的方便和准确性,此次模拟采用的是DOS model[20]。计算时,输入各种光学参数,即可根据控制变量法,模拟出不同情况下太阳电池的光电转换率乃至其他的光学参数。InxGa1-xN系列合金的物理特性和光学特性都与In组分大小密切相关,通过GaN和InN参数的线性拟合,可以获得InGaN的部分参数(表 1)。
| 表 1 InxGa1-xN系列合金的各项参数计算公式 Table 1 The calculation formula of each parameter about InxGa1-xN series alloys |
对于电子亲和势χ (Electron affinity, 单位eV),有[21]:
| $ \chi = \chi \left( {{\rm{GaN}}} \right) + 0.7\left( {{E_{\rm{g}}}\left( {{\rm{GaN}}} \right)-{E_{\rm{g}}}\left( {{\rm{InGaN}}} \right)} \right), $ | (4) |
式中χ(GaN)=4.1 eV。
对于迁移率(Mobilities),具有如下形式[22]:
| $ {\mu _i}\left( N \right) = {\mu _{\min, i}} + \frac{{{\mu _{\max, i}}-{\mu _{\min, i}}}}{{1 + {{\left( {\frac{N}{{{N_{g, i}}}}} \right)}^{{\gamma _i}}}}}, $ | (5) |
式中i代表电子或空穴,表示载流子类型;N为掺杂浓度;μmax, i、μmin, i,Ng, i, γi都是由材料本身决定的参数,如表 2所示。
| 表 2 InGaN的迁移率公式中的各参数取值[22] Table 2 The value of each parameter in the mobilities formula of InGaN[22] |
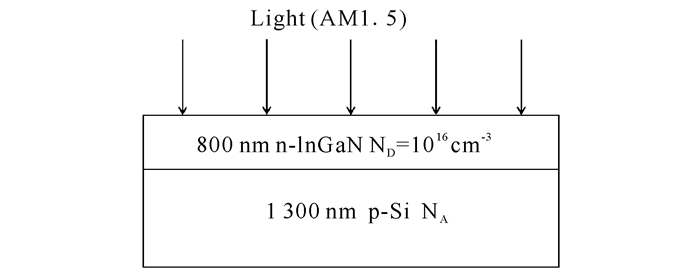
本计算所模拟的InGaN/Si异质单结太阳电池为垂直结构,由厚度为1 300 nm的p-Si层和厚度为800 nm的n-InGaN层构成(图 1)。
|
图 1 InGaN/Si异质单结太阳电池的结构示意图 Fig.1 Schematic diagram of InGaN/Si single-heterojunction solar cells structure |
在模拟过程中,设定InGaN中的In组分为65%(Eg=1.32 eV),同时设定n-InGaN的掺杂浓度为1016 cm-3且保持不变,通过改变p-Si的掺杂浓度NA的值,得到相应条件下的电流密度JSC、光电转换效率Eff、填充因子FF和开路电压VOC的数据,绘制JSC、Eff、FF和VOC与p-Si掺杂浓度NA之间的变化关系曲线,分析造成这些变化的原因。设定条件后的In0.65Ga0.35N/Si异质单结太阳电池的有关基本参数设置如表 3所示。
| 表 3 In0.65Ga0.35N/Si异质单结太阳电池的基本参数设置 Table 3 Basic parameter settings of In0.65Ga0.35N/Si heterojunction solar cells in AMPS-1D |
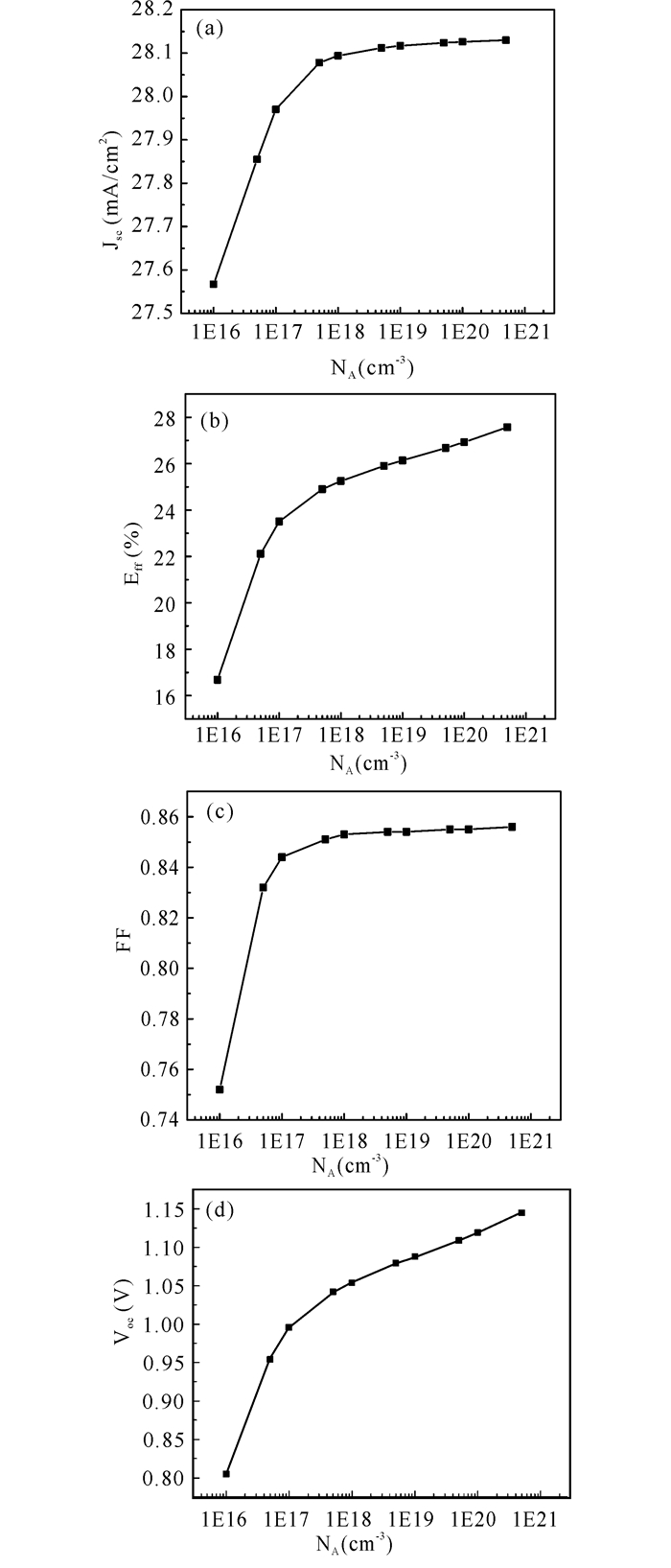
如图 2所示,In0.65Ga0.35N/Si异质单结太阳电池的电流密度JSC随着p-Si掺杂浓度NA的增大而增大,但在掺杂浓度较低时,略微增大掺杂浓度,电流密度便会呈明显升高的趋势;在一定高的掺杂浓度范围内(NA>5.00×1017 cm-3时),增大掺杂浓度,电流密度基本保持不变(图 2a)。在低的p-Si掺杂浓度下模拟得到的太阳电池的光电转换效率较低,仅为16.68%,而当掺杂浓度升高时,光电转换效率得到显著提高(图 2b)。值得一提的是,本实验只模拟到p-Si掺杂浓度NA为5×1020 cm-3,并不意味着越来越高的掺杂浓度就一定有更高的光电转换效率,具体情况还有待进一步探讨。在掺杂浓度较低时填充因子也较低,但随着掺杂浓度的增加,填充因子的值将增大,并且在高浓度的范围内(NA>5.00×1017 cm-3时)保持在0.85左右且变化不大;开路电压的值也与掺杂浓度的大小呈正相关关系,随着掺杂浓度的增加,开路电压VOC的值缓慢增大(图 2c~d)。
|
图 2 JSC(a)、Eff (b)、FF(c)和VOC (d)与掺杂浓度NA的变化关系 Fig.2 Relationship between JSC (a), Eff(b), FF (c) and VOC (d) and doping concentration NA |
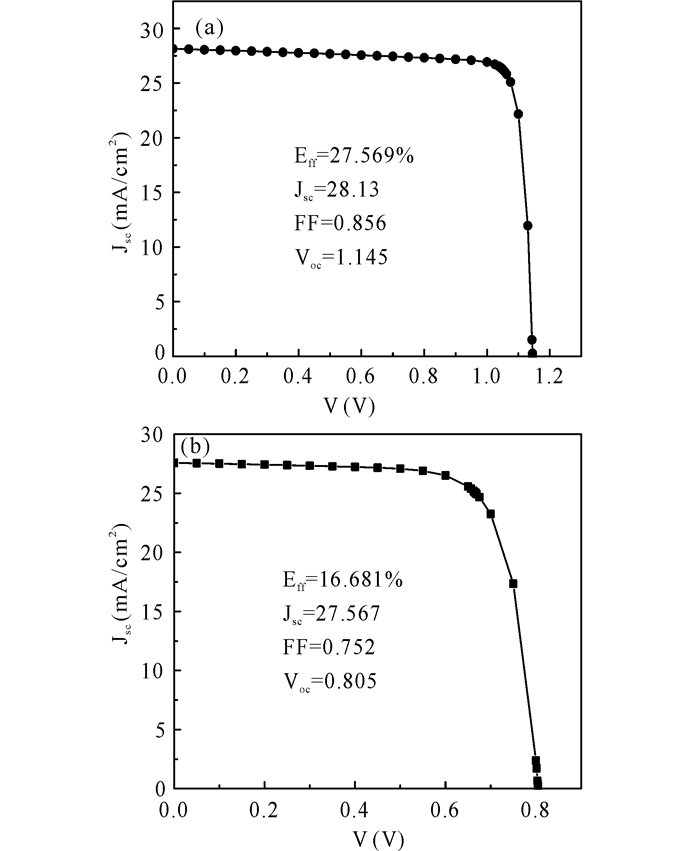
由图 3a可以看出,在NA=5×1020 cm-3的高掺杂浓度下,电池的开路电压约为1.15 V,电流密度约为28 mA/cm2,光电转换效率达到了27.569%,说明此状态下的电池工作性能良好;对比图 3b可以看到,在NA=1×1016 cm-3的低掺杂浓度下,电池的开路电压约为0.8 V,电流密度约为27 mA/cm2,光电转换效率为16.681%,远低于具有高掺杂浓度的p-Si衬底的异质单结太阳电池。
|
(a)NA=5×1020 cm-3; (b) NA=1×1016 cm-3 图 3 不同p-Si衬底掺杂浓度下的太阳电池J-V曲线 Fig.3 The J-V curve of solar cells at different doping concentrations of p-type Si substrate |
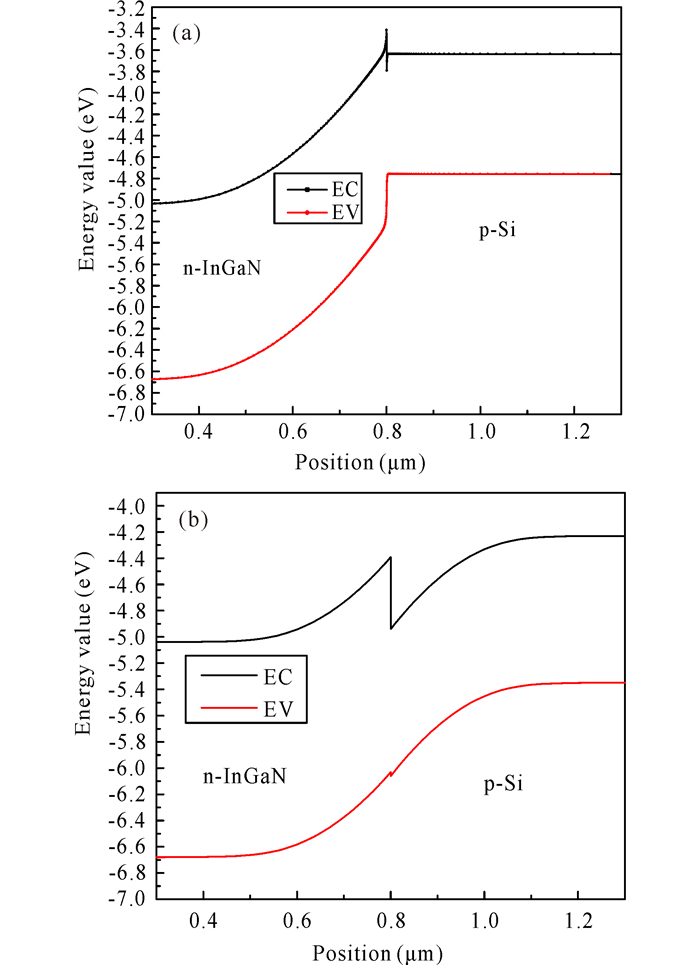
由图 4可知,导带EC有一处尖峰势垒,正是这个尖峰势垒影响了电子的正常移动。由于InGaN/Si为异质结结构,其交界面能带是不连续的,当电子从p区移动到n区时会受到尖峰势垒的阻碍,势能差使得电子无法正常移动。当掺杂浓度较高时,对应的窄带材料区域的掺杂浓度就会高,势垒落在另外一个区域,即宽带的空间电荷区,此时的尖峰势垒高度是正值,有利于电子等粒子的通过;相反,相应的低浓度掺杂电池的尖峰势垒高度为负值,电子会在尖峰势垒处聚集,不利于通过,所以在一定程度上低掺杂浓度的太阳电池的光电转换效率会比高掺杂浓度的太阳电池的效率要低。
|
(a)NA=5×1020 cm-3; (b)NA=1×1016 cm-3 图 4 不同p-Si衬底掺杂浓度下的平衡能带图 Fig.4 Equilibrium band diagram at different doping concentrations of p-type Si substrate |
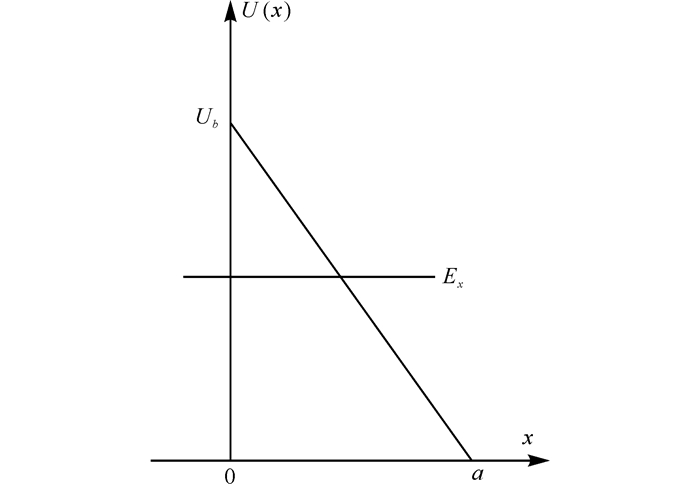
另外,尖峰势垒本身的高度和宽度也会影响载流子的移动。尖峰势垒在量子力学中可以等价为一个三角形势垒,如图 5所示。关于高度和宽度的影响关系可以用量子力学的内容去说明。对于三角形势垒的计算有下列情况:
|
图 5 三角形势垒示意图 Fig.5 Schematic diagram of triangular barrier |
三角形势垒计算公式为
| $ a = \frac{{{U_0}}}{{q{F_x}}}, $ | (6) |
其中U0为势垒的高度,a为势垒的宽度,Fx为电场。
而三角形势垒的隧穿效率计算公式为
| $ D\left( {{E_x}} \right) = \exp \left[{-\frac{{4\sqrt {2m_2^*} }}{{3q\hbar {F_x}}}{{\left( {{U_0}-{E_x}} \right)}^{\frac{3}{2}}}} \right], $ | (7) |
其中2m2*为有效的粒子质量,
| $ D\left( {{E_x}} \right) = \exp \left[{-\frac{{4\sqrt {2m_2^*} }}{{3q\hbar {F_x}}}U_0^{\frac{3}{2}}} \right], $ | (8) |
联立式(5)和式(7)两个公式可以推出:
| $ D\left( {{E_x}} \right) = \exp \left[{-\frac{{4a\sqrt {2m_2^*} }}{{3\hbar }}U_0^{\frac{3}{2}}} \right]。$ | (9) |
由公式(9)可以清楚地看到,当增大势垒高度U0和宽度a时,隧穿效率D(Ex)将减小,清楚地解释了在较低的掺杂浓度(NA=1×1016cm-3)下,尖峰势垒的高度和宽度都比高掺杂浓度(NA=5×1020cm-3)时大得多,所以异质结的隧穿效率很低,因而电池的光电转换效率也很低。
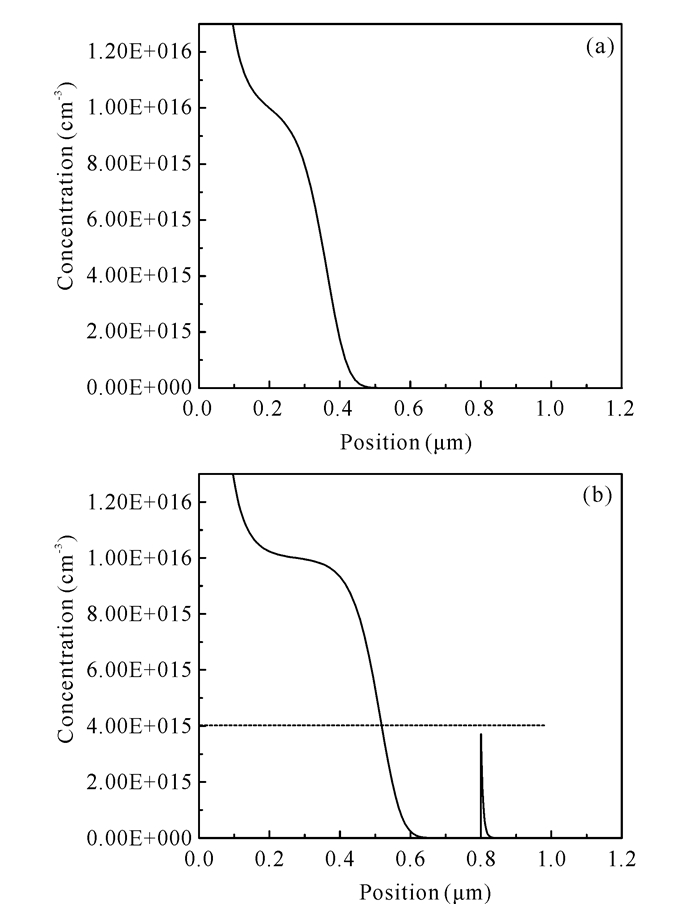
由图 6可以看出,在较高的掺杂浓度(NA=5×1020cm-3)下,p-Si衬底的电子分布比较均匀;在较低的掺杂浓度(NA=1×1016 cm-3)下,在0.8 μm的位置有大量的电子聚集,说明低掺杂浓度的太阳电池尖峰势垒的势能差比较大,不利于电子的正常移动,故光电转换效率较低。
|
(a) NA=5×1020 cm-3; (b) NA=1×1016 cm-3 图 6 不同p-Si衬底掺杂浓度下的E-L电子分布 Fig.6 E-L electron distribution at different doping concentrations of p-type Si substrate |
利用AMPS-1D模拟软件研究了p-Si的掺杂浓度对InGaN/Si异质单结太阳电池性能的影响,主要结论如下:
1) p-Si衬底的掺杂浓度对InGaN/Si异质单结太阳电池的性能有明显影响。随着掺杂浓度NA的升高,电流密度JSC和填充因子FF随之升高,当到达一定高的掺杂浓度范围时(NA>5.00×1017 cm-3),JSC基本保持不变,约为28.12 mA/cm2;FF保持在0.85左右,变化不大;随着掺杂浓度NA的升高,开路电压VOC和光电转换效率Eff缓慢增大,与NA大小呈正相关关系,但并不意味着更高的掺杂浓度就一定能获得更高的光电转换效率,有待进一步探究。
2) 高掺杂浓度下的太阳电池具有较好的光电转换效率。低掺杂浓度的太阳电池光电转换效率较低,是因为其对应的尖峰势垒高度和宽度均较大,影响了光生载流子的输运。
| [1] |
广西科学院学报编辑部. 中国新能源产业异军突起[J]. 广西科学院学报, 2011, 27(2): 87. The Editorial Office of Journal of Guangxi Academy of Sciences. Rapid development of New Energy in China[J]. Journal of Guangxi Academy of Sciences, 2011, 27(2): 87. |
| [2] |
黄志民. 开发广西太阳能资源的可行性[J]. 广西科学院学报, 1992, 8(1): 94-98. HUANG Z M. The feasibility of developing Guangxi's solar energy resource[J]. Journal of Guangxi Academy of Sciences, 1992, 8(1): 94-98. |
| [3] |
李福宾, 林硕, 李建功, 等. GaN肖特基紫外探测器的电流输运研究[J]. 广西科学, 2009, 16(2): 158-160. LI F B, LIN S, LI J G, et al. Current transport of GaN Schottky UV detectors[J]. Guangxi Sciences, 2009, 16(2): 158-160. |
| [4] |
WU J, WALUKIEWICZ W, YU K M, et al. Unusual properties of the fundamental band gap of InN[J]. Appl Phys Lett, 2002, 80(21): 3967-3969. DOI:10.1063/1.1482786 |
| [5] |
DAVYDOV V Y, KLOCHIKHIN A A, EMTSEV V V, et al. Band gap of hexagonal InN and InGaN alloys[J]. Phys Stat Sol:B, 2002, 234(3): 787-795. DOI:10.1002/(ISSN)1521-3951 |
| [6] |
DAVYDOV V Y, KLOCHIKHIN A A, SEISYAN R P, et al. Absorption and emission of hexagonal InN.Evidence of narrow fundamental band gap[J]. Phys Stat Sol:B, 2002, 229(3): R1-R3. DOI:10.1002/(ISSN)1521-3951 |
| [7] |
WU J, WALUKIEWICZ W, YU K M, et al. Superior radiation resistance of In1-xGaxN alloys:Full-solar-spectrum photovoltaic material system[J]. Journal of Applied Physics, 2003, 94(10): 6477-6482. DOI:10.1063/1.1618353 |
| [8] |
AGER Ⅲ J W, WALUKIEWICZ W. High efficiency, radiation-hard solar cells[R]. Lawrence Berkeley National Laboratory Report, 2004.
|
| [9] |
WU M H, CHANG S P, CHANG S J, et al. Characteristics of GaN/InGaN double-heterostructure photovoltaic cells[J]. International Journal of Photoenergy, 2012(1): 174-178. |
| [10] |
BAE S Y, SHIM J P, LEE D S, et al. Improved photovoltaic effects of a vertical-type InGaN/GaN multiple quantum well solar cell[J]. Jpn J Appl Phys, 2011, 50(9): 092301. DOI:10.1143/JJAP.50.092301 |
| [11] |
BAI J, YANG C C, ATHANASIOU M, et al. Efficiency enhancement of InGaN/GaN solar cells with nanostructures[J]. Appl Phys Lett, 2014, 104(5): 051129. DOI:10.1063/1.4864640 |
| [12] |
CHANG Y A, CHEN F M, TSAI Y L, et al. Fabrication and characterization of back-side illuminated InGaN/GaN solar cells with periodic viaholes etching and Bragg mirror processes[J]. Optics Express, 2014, 22(5): A1334-A1342. |
| [13] |
CAI X, WANG Y, CHEN B, et al. Investigation of InGaN p-i-n homojunction and heterojunction solar cells[J]. IEEE Photonics Technology Letters, 2013, 25(1): 59-62. DOI:10.1109/LPT.2012.2227702 |
| [14] |
YANG C B, WANG X L, XIAO H L, et al. Photovoltaic effects in InGaN structures with p-n junctions[J]. Physica Status Solidi:A, 2007, 204: 4288-4291. DOI:10.1002/pssa.v204:12 |
| [15] |
ZHANG X B, WANG X L, XIAO H L, et al. Simulation of In0.65Ga0.35N single-junction solar cell[J]. Journal of Physics D:Applied Physics, 2007, 40(23): 7335-7338. DOI:10.1088/0022-3727/40/23/013 |
| [16] |
周梅, 赵德刚. 结构参数对p-i-n结构InGaN太阳能电池性能的影响及机理[J]. 物理学报, 2012, 61(16): 168402. ZHOU M, ZHAO D G. Influence of structure parameters on the performance of p-i-n InGaN solar cell[J]. Acta Physica Sinica, 2012, 61(16): 168402. DOI:10.7498/aps.61.168402 |
| [17] |
文博, 周建军, 江若琏, 等. InGaN太阳电池转换效率的理论计算[J]. 半导体学报, 2007, 28(9): 1392-1395. WEN B, ZHOU J J, JIANG R L, et al. Theoretical calculation of conversion efficiency of InGaN solar cells[J]. Chinese Journal of Semiconductors, 2007, 28(9): 1392-1395. |
| [18] |
张聪亮. 硅基薄膜太阳电池的数值模拟[D]. 温州: 温州大学, 2011. ZHANG C L. Numerical simulation of silicon-based thin-film solar cells[D]. Wenzhou: Wenzhou University, 2011. |
| [19] |
LIN S, LI X R, PAN H Q, et al. Numerical analysis of InxGa1-xN/SnS and AlxGa1-xN/SnS heterojunction solar cells[J]. Energy Conversion and Management, 2016, 119(1): 361-367. |
| [20] |
张利超. InGaN基太阳电池的结构设计及极化效应研究[D]. 石家庄: 河北科技大学, 2015. ZHANG L C. Structural design and polarization effect of InGaN-based solar cells[D]. Shijiazhuang: Hebei University of Science and Technology, 2015. |
| [21] |
LEVINSHTEIN M E, RUMYANTSEV S L, SHUR M S. Properties of advanced semiconductor materials[M]. Chichester, UK: Wiley, 2001.
|
| [22] |
MNATSAKANOV T T, LEVINSHTEIN M E, POMORTSEVA L I, et al. Carrier mobility model for GaN[J]. Solid-State Electronics, 2003, 47(1): 111-115. DOI:10.1016/S0038-1101(02)00256-3 |
 2017, Vol. 24
2017, Vol. 24 


