【研究意义】近年来，钽碳化物由于其具有优异的物理性质，如高硬度和高熔点，高导热和导电系数，良好的热稳定性和耐腐蚀性能，使其在切削工具、硬质合金、国防科技、航天航空等领域内得到广泛应用^[1-2]。【前人研究进展】目前TaC被用作硬质合金烧结晶粒长大抑制剂，对抑制晶粒长大有明显效果^[3]。有研究指出与TaC比较，Ta₂C的塑性较好，抗氧化性能更好，但强度较低^[4-5]。据报道，基于密度泛函理论的第一性原理计算可用于计算钽碳化物的电子结构、弹性常数等物理性质^[6-8]。其中，Yu等^[8]利用USPEX软件结合VASP对40余种Ta和C的二元化合物进行模拟计算和结构稳定性预测，发现TaC、Ta₂C、Ta₆C₅是稳定的结构，而Ta₄C₃和Ta₃C₂的能量稍高。【本研究切入点】然而实验上，只发现TaC、Ta₂C和Ta₄C₃ 3种化合物。截止目前为止，很少有理论对这些化合物在高温高压下的热力学性质进行研究。【拟解决的关键问题】本研究拟利用第一性原理结合德拜模型对TaC、Ta₂C和Ta₄C₃ 3个化合物的弹性常数、电子结构以及高温高压下热力学性质进行计算研究，为进一步开展研究提供参考。

采用基于密度泛函理论的第一性原理计算软件VASP^[9-10]对研究对象进行计算。在计算中采用投影缀加波方法(PAW)^[11-12]，交换关联势则采用广义梯度近似下的PBE方案^[13]，布里渊区积分采用Monkhorst Pack方法^[14]。在本研究计算中截断能设置为600 eV，能量收敛精度为1×10^-6 eV。计算结果误差小于1.0 meV/atom。有关计算弹性常数以及德拜模型的方法参见文献[15-17]。

利用第一性原理计算的3个化合物的晶格常数和形成焓列在表 1中，为了进行比较，晶格常数实验值和形成焓的其他理论值也列于其中。比较发现本研究计算的晶格常数和Villars等^[18]的实验值非常吻合，表明本研究计算结果正确。形成焓也与Yu等^[8]所计算的值一致。为了进一步研究3个化合物的力学性质，本研究计算了3个化合物的单晶弹性常数，计算值列于表 1中。将本研究获得的弹性常数计算值与Sahnoun等^[6]和Yu等^[8]所计算的值进行比较发现，对于TaC的弹性常数，Sahnoun等^[6]获得的C₄₄明显比本研究以及Yu等^[8]的计算值大将近1倍，而本研究的计算值和Yu等^[8]的一致。Ta₂C和Ta₄C₃的弹性常数与Yu等^[8]的计算值比较发现，除了Ta₄C₃的C₁₄有差别外，其他都一致。经过反复验证，本研究的计算过程和计算结果正确。

表 1(Table 1)

表 1 Ta-C系3个二元化合物的晶格常数、形成焓ΔH、弹性常数Cij Table 1 The lattice constants, enthalpy of formation ΔH, elastic constants Cij of 3 binary compounds of Ta-C system 化合物 Compounds 晶格常数 Lattice constants(Å) ΔH(eV/atom) 弹性常数 Elastic constants (GPa) a c C11 C12 C13 C14 C33 C44 TaC 4.475 4.46[18] -0.586 -0.59[8] 749.7 732.86[6] 737[8] 135.2 112.04[6] 141[8] 172.7 315.47[6] 175[8] Ta2C 3.119 3.10[18] 4.955 4.94[18] -0.603 -0.60[8] 478.2 479[8] 171.4 164[8] 147.3 149[8] -49.9 -45[8] 517.0 500[8] 133.2 133[8] Ta4C3 3.145 3.12[18] 30.852 30.06[18] -0.617 -0.62[8] 552.5 571[8] 175.2 156[8] 172.2 169[8] -70 47[8] 534.1 537[8] 182.9 179[8]

表 1 Ta-C系3个二元化合物的晶格常数、形成焓ΔH、弹性常数Cij Table 1 The lattice constants, enthalpy of formation ΔH, elastic constants Cij of 3 binary compounds of Ta-C system

经比较发现，本研究获得的多晶体积模量、剪切模量以及杨氏模量等计算值和Yu等^[8]的计算值一致，TaC的体积模量最大，其次是Ta₄C₃，最后是Ta₂C，杨氏模量和剪切模量也和体积模量具有一样的趋势(表 2)。由图 1可以看出，由于TaC具有立方晶系的结构，因此杨氏模量在各个方向都具有相同的值，呈球形，各向异性小；而Ta₂C和Ta₄C₃两个化合物由于具有三角晶系的结构，因此，这两个化合物的杨氏模量具有各向异性值，Ta₂C呈扁平状，而Ta₄C₃在Z轴上带有上下两个尖角。从B/G值来看，TaC的脆性最大，其次是Ta₄C₃，最后是Ta₂C，因此本研究计算也证实了Wang等^[4]和Leon等^[5]所得到的结论：与TaC比较，Ta₂C的塑性较好，但强度较低。

表 2(Table 2)

表 2 Ta-C系3个二元化合物的体积模量B、剪切模量G、杨氏模量E、B/G值、泊松比σ、声速和德拜温度Θ Table 2 The bulk modulus B, shear modulus G, Young's modulus E, B/G value, Poisson's ratio σ, sound speed, Debye temperature Θ of 3 binary compounds of Ta-C system 化合物 Compounds B (GPa) G (GPa) E (GPa) B/G σ 声速Sound speed (m/s) Θ (K) vl vt vm TaC 340.1 339.67[8] 217.9 216.90[8] 538.7 1.56 0.236 6 638.3 3 902.6 4 325.6 569.2 Ta2C 267.3 264.66[8] 142.3 148.08[8] 362.6 1.88 0.274 5 542.1 3 092.8 3 443.4 425.0 Ta4C3 297.5 296[8] 174.6 187[8] 438.2 1.70 0.255 6 035.3 3 463.4 3 847.0 493.8

表 2 Ta-C系3个二元化合物的体积模量B、剪切模量G、杨氏模量E、B/G值、泊松比σ、声速和德拜温度Θ Table 2 The bulk modulus B, shear modulus G, Young's modulus E, B/G value, Poisson's ratio σ, sound speed, Debye temperature Θ of 3 binary compounds of Ta-C system

图 1 (Fig. 1)

图 1 3个化合物TaC、Ta2C、Ta4C3的杨氏模量各向异性 Fig.1 Anisotropy of Young's modulus for three compounds TaC, Ta2C and Ta4C3

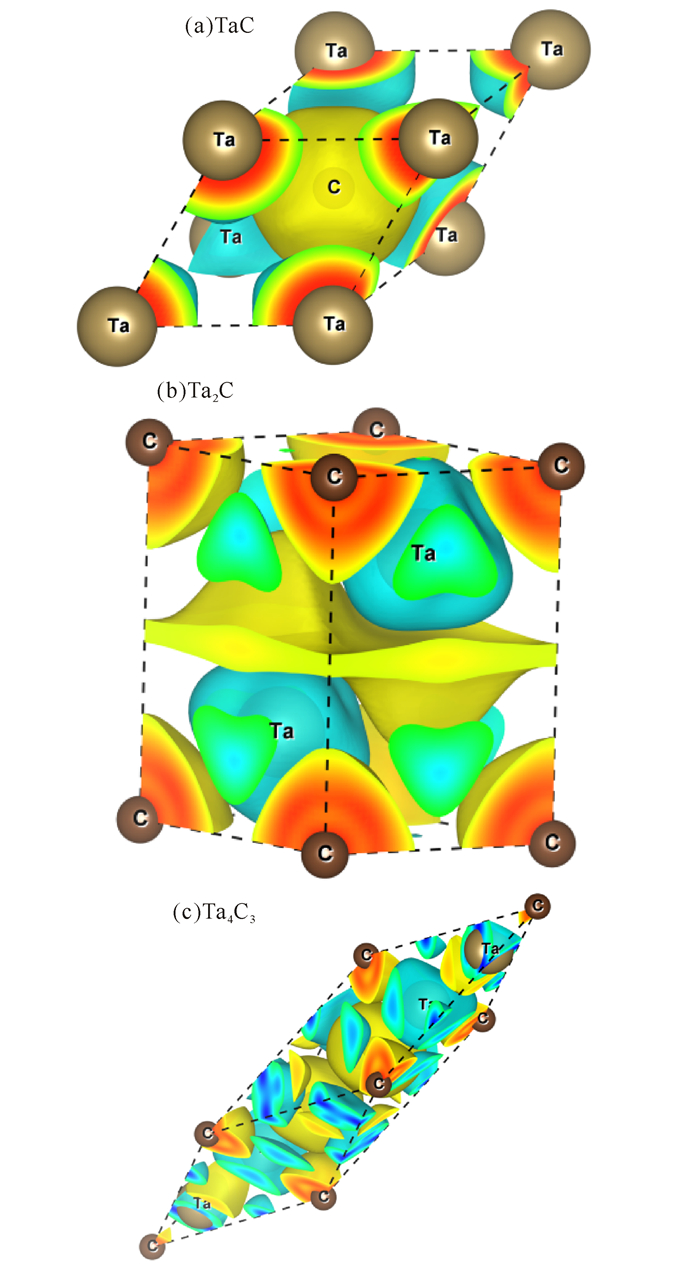
如图 2所示，计算显示3个化合物都呈现金属性质，费米面附近都是由Ta的d态电子主导。在-15~-10 eV区间，态密度主要是由C的s态电子贡献；在-10~0 eV区间，C的p态电子和Ta的p态以及d态电子共同贡献并产生杂化效应；在费米能级以上主要来自Ta的d态电子的贡献。由图 3可知，Ta和C之间结合类型是离子键的结合方式，和Yu等^[8]给出的共价键结合方式不同。因为电子都在各个原子周围，原子间并没有电子的集中情况。

图 2 (Fig. 2)

(a)TaC; (b) Ta2C; (c) Ta4C3 图 2 3个化合物TaC、Ta2C、Ta4C3的电子态密度 Fig.2 The electronic density of states for three compounds TaC, Ta2C and Ta4C3

图 3 (Fig. 3)

图 3 3个化合物TaC、Ta2C、Ta4C3的电荷密度分布 Fig.3 The charge densities of three compounds TaC, Ta2C and Ta4C3

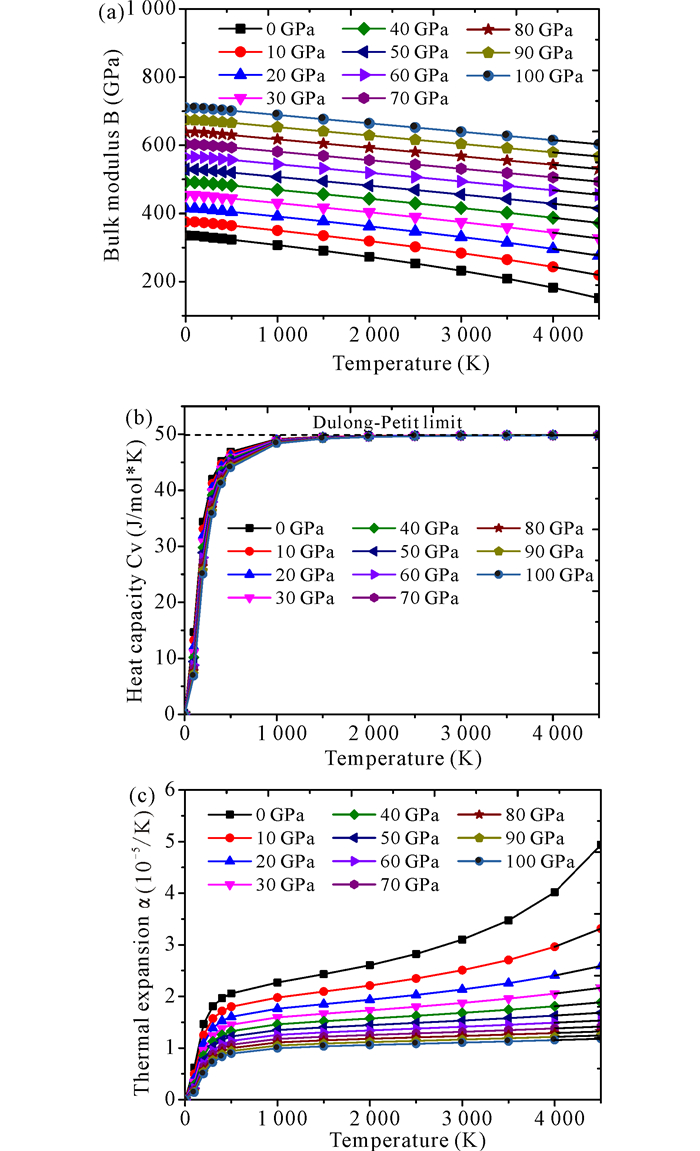
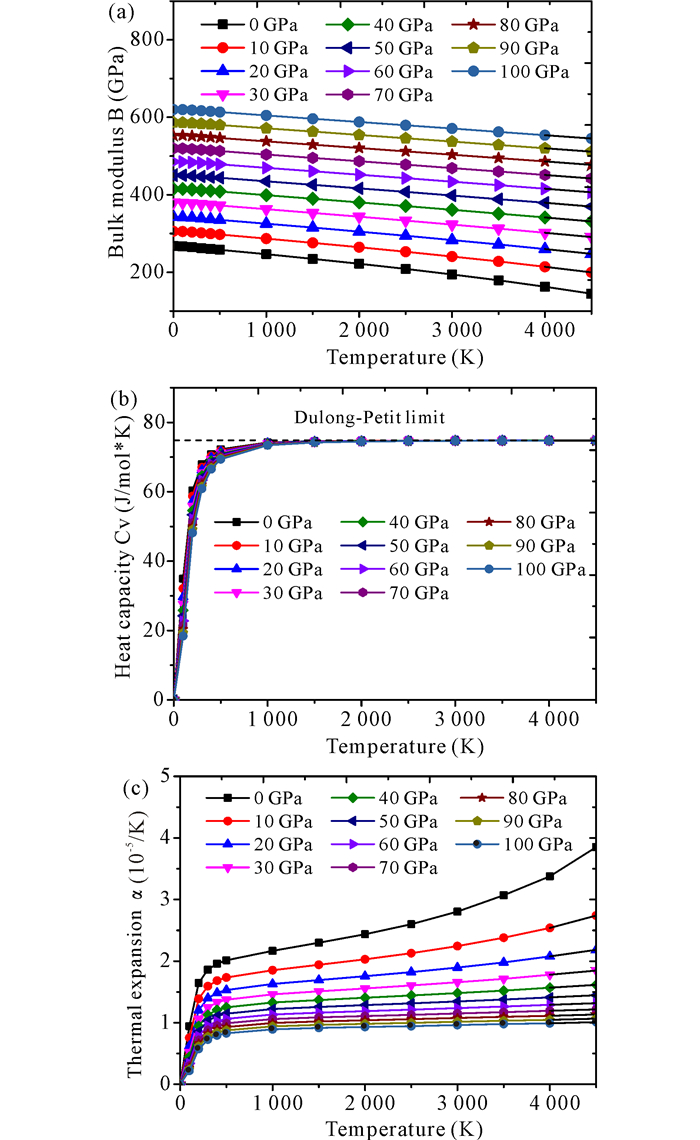
为了获得钽碳化物在高温高压下的性能，利用徳拜模型计算高温(0~4 500 K)高压(0~100 GPa)下3个化合物的体积模量、热容以及热膨胀系数随压强和温度增加的变化情况。结果如图 4~6所示，TaC的体积模量随着温度的增加而减小，随着压强的增加而增大，并且体积模量在高压下随温度增加而减小的幅度比低压下的幅度小。热容的计算值显示随着温度的增加，热容从0增加到一定的值，无限接近杜隆-珀蒂极限值，并且高温下，无论压强怎么变化，其极限值是一样的，即压强不改变热容极限值。但是在1 000 K以下，压强对热容的影响是压强越大热容值越小。热膨胀系数计算值显示随着温度的增加，热膨胀系数也在增加，而随着压强的增加，热膨胀系数减小；并且热膨胀系数在高压下随温度的变化率减小。由此可见，高压下热膨胀系数比低压下的热膨胀系数低。其余两个化合物呈现和TaC类似的变化趋势。

图 4 (Fig. 4)

图 4 TaC的体积模量、热容量以及热膨胀系数随温度和压强的变化 Fig.4 Bulk modulus, heat capacity and thermal expansion coefficient vs temperature at various pressures of TaC

图 5 (Fig. 5)

图 5 Ta2C的体积模量、热容量以及热膨胀系数随温度和压强的变化 Fig.5 Bulk modulus, heat capacity and thermal expansion coefficient vs temperature at various pressures of Ta2C

图 6 (Fig. 6)

图 6 Ta4C3的体积模量、比热容以及热膨胀系数随温度和压强的变化 Fig.6 Bulk modulus, heat capacity and thermal expansion coefficient vs temperature at various pressures of Ta4C3

用基于密度泛函理论的第一性原理方法计算了Ta-C二元系中3个化合物的晶格常数、形成焓、电子结构、弹性性质等，并结合德拜模型获得了高温高压下3个化合物的热物理性能。结论如下：TaC、Ta₂C以及Ta₄C₃3个化合物的晶格常数、形成焓以及弹性常数计算值和实验值或其他理论值吻合。弹性模量的计算值表明，TaC的体积模量、剪切模量和杨氏模量最大，其次是Ta₄C₃，最后是Ta₂C；同时TaC的脆性最大，Ta₂C的延展性最好。电子结构特性显示Ta的d态电子与C的p态电子杂化，具有离子键的特征。体积模量随温度增加而减小，随压强增加而增大；热容随温度增加而增大并无限接近杜隆-珀蒂极限值，压强对热容的影响低温下显著而高温下影响小；随着温度的增加，热膨胀系数增加，高压下热膨胀系数变化率减小。