2. 广西大学物理科学与工程技术学院,广西南宁 530004
2. College of Physics Science and Engineering, Guangxi University, Nanning, Guangxi, 530004, China
【研究意义】三叉晶界是三条晶界相遇时形成的线缺陷,具有不同于晶界的独特热力学和动力学性质[1]。三叉晶界作为新相形核、空洞和腐蚀的首选位置以及溶质原子扩散的有利通道[2],在晶粒长大及塑性变形过程中起重要作用。因此研究三叉晶界的迁移过程及其影响因素具有重要意义。【前人研究进展】目前,已有学者对三叉晶界迁移进行实验研究。1998年,Czubayko等[3]利用电子背散射衍射(EBSD)原位观察金属锌(Zn)的三叉晶界运动过程,并观察到三叉晶界迁移动力学向晶界迁移动力学的转变。2001年,Protasova等[4]研究发现金属铝(Al)中三叉晶界的缓慢移动能够控制晶界系统的运动。2005年,Mattissen等[5]利用扫描电镜(SEM)原位研究Al中三叉晶界对晶粒长大动力学的影响,发现三叉晶界对晶界运动和晶粒长大动力学均有显著影响。2017年,尹文红等[6]采用EBSD技术研究不同变形量高纯Al退火后三叉晶界及晶界的迁移行为。结果表明,三叉晶界及其晶界的迁移量随着变形量的增加而增大,且三叉晶界的迁移距离比晶界的小。但上述研究尚未达到原子尺度。由于晶界通常只有几个原子层厚,难以通过实验直接原位观测,因此计算机模拟已经成为研究该问题的重要方法。在三叉晶界的原子尺度模拟方面,分子动力学(Molecular Dynamics,MD)是常用方法之一。1999年,Upmanyu等[7]利用MD研究了单个三叉晶界的迁移过程,结果表明动态三叉晶界角度与晶粒尺寸和晶界取向差有关。2009年,Frolov等[1]采用MD模拟了三叉晶界的自扩散过程,研究表明三叉晶界扩散比晶界扩散更快。2014年,Trautt和Mishin[8]采用MD研究了三晶系统中晶界运动和晶粒旋转现象,结果表明三叉晶界不能阻止晶粒旋转,但可以显著减缓旋转过程。【本研究切入点】尽管MD在材料的原子尺度模拟方面取得了很多进展[9],但该方法主要适用于原子振动的时间尺度(10-14~10-12 s),难以扩展到原子扩散的时间尺度(10-6 s)。2002年,Elder等[10]基于经典密度泛函理论(CDFT)提出的晶体相场(Phase Field Crystal,PFC)模型克服了MD的上述缺点,不仅能够在原子空间尺度和扩散时间尺度上研究材料微观结构演化,还能够自洽地耦合弹性能和各向异性等特征[11]。因此,PFC模型自提出以来得到了广泛应用和发展,已被用于研究晶体形核[12]、准晶生长[13]、动态回复[14]、裂纹扩展[15-17]和金属互连电迁移[18-19]等现象。目前,虽然已有学者利用PFC方法研究了将一个圆形晶粒嵌入双晶系统中圆形晶粒的收缩过程,以及三叉晶界处位错的反应及应变[20-21]。但利用PFC方法研究恒定曲率条件下三叉晶界的迁移过程,还未见报道。【拟解决的关键问题】本研究采用PFC方法研究包含一个环形晶粒的三晶系统中三叉晶界的迁移过程,探究晶界曲率对三叉晶界迁移的影响。
1 模型与方法 1.1 PFC模型PFC模型采用具有周期结构特征的局域原子密度作为序参量。在固液系统中,无量纲的自由能函数F可以构造为[11]
| $ F{\rm{ = }}\int {\left\{ {\frac{\psi }{2}\left[{\gamma {\rm{ + }}{{\left( {1{\rm{ + }}{\nabla ^2}} \right)}^2}} \right]\psi {\rm{ + }}\frac{{{\psi ^4}}}{4}} \right\}{\rm{d}}r}, $ | (1) |
式中,γ为与温度相关的唯象参数;∇2为Laplace算符;ψ为原子密度,其通用形式可表示为[11]
| $ \psi \left( {r, t} \right) = \sum\limits_{n, m} {{a_{n, m}}{e^{i{{\vec G}_{n, m}} \cdot \vec r}}} + {\psi _0}, $ | (2) |
式中,右边第1项反映晶格原子的周期结构特征,第2项ψ0为平均原子密度,反映液相的原子均匀无序特征;
| $ {\vec b_1} = \frac{{2\pi }}{{{r_0}\sqrt 3 /2}}\left( {\sqrt 3 /2\hat x + \hat y/2} \right), {\vec b_2} = \frac{{2\pi }}{{{r_0}\sqrt 3 /2}}\hat y, $ | (3) |
式中,r0为最近邻原子间距,
二维情况下,三角相的原子密度ψ的表达式为[11]
| $ \begin{array}{l} \psi = A\left[{\cos \left( {{q_t}x} \right)\cos \left( {{q_t}y/\sqrt 3 } \right)-} \right.\\ \left. {\cos \left( {2{q_t}y/\sqrt 3 } \right)/2} \right] + {\psi _0}, \end{array} $ | (4) |
式中,A为反映原子密度周期结构的振幅;qt为波数,满足qt=2π/r0。将(4)式代入(1)式,并对A和qt分别求导,求出自由能密度函数的极值,便可求得A和qt的值[11]
| $ A = 4/15\left( {3{\psi _0} + \sqrt {-15\gamma-36\psi _0^2} } \right), {q_t} = \sqrt 3 /2, $ | (5) |
原子密度ψ是一个保守场变量,其随时间演化用Cahn-Hilliard动力学方程描述[11]
| $ \begin{array}{l} \frac{{\partial \psi }}{{\partial t}} = {\nabla ^2}\frac{{\delta F}}{{\delta \psi }} + \zeta = {\nabla ^2}\left\{ {{\psi ^3} + \left[{\gamma + \left( {1 + } \right.} \right.} \right.\\ \left. {\left. {{{\left. {{\nabla ^2}} \right)}^2}} \right]\psi } \right\} + \zeta, \end{array} $ | (6) |
式中,ζ为满足两点相关性的Gauss噪声。在本研究中不考虑噪声的作用。
为提高计算效率,可采用半隐式Fourier谱方法[22]求解动力学方程,可得
| $ {\hat \psi _{n + 1}} = \frac{{{{\hat \psi }_n}- {k^2}\Delta t\hat \psi _n^3}}{{1 + {k^2}\Delta t\left[{\gamma + {{\left( {1-{k^2}} \right)}^2}} \right]}}, $ | (7) |
式中,
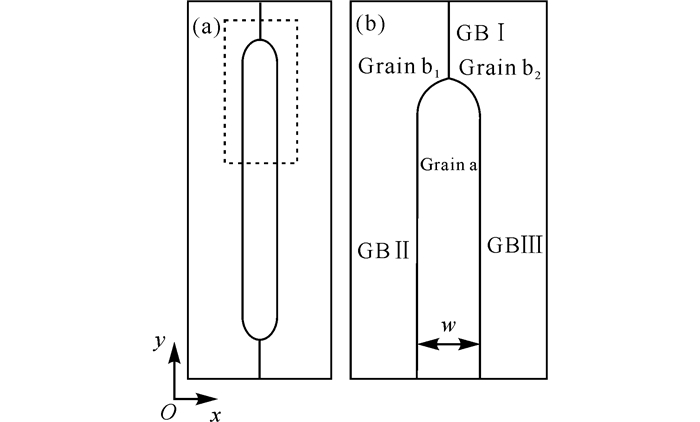
图 1中将一个环形晶粒(晶粒a)嵌入到双晶(晶粒b1和b2)系统中,组成一个三晶系统。晶粒a、b1和b2三者相交形成三叉点,其中晶粒a的宽度为w,其顶部的晶界曲率为κ(κ=2/w)。计算时将连续空间离散为四方网格,计算区域网格为Lx△x×Ly△y,取空间步长△x=△y=π/4,时间步长Δt=0.5,时间步用ts表示。具体参数设置:采用三角相表征晶体相,选取(ψ0, γ)=(0.21, -0.12);尺寸Lx×Ly为800×1 600,晶粒a、b1和b2的取向角度分别为0°、22.5°和-22.5°。晶粒a与晶粒b1、b2之间的晶界(GBⅡ和GBⅢ)为非对称倾侧晶界,取向差分别为±22.5°;晶粒b1和b2之间的晶界(GBⅠ)为对称倾侧晶界,取向差为45°。
|
(b)为(a)中方框的放大图 (b) is the magnified image of the box in (a) 图 1 模拟所用的几何构型示意图 Fig.1 Schematic diagram of the geometry employed in the simulation |
为了清晰地显示三叉晶界的迁移过程,重点对图 1b所示区域进行观测,其尺寸为400×600,约3.23×103个原子。从图 1b可见,晶界Ⅰ(GBⅠ)是一条平直晶界,晶界Ⅱ(GBⅡ)和晶界Ⅲ(GBⅢ)都是由一段弧形晶界和平直晶界组成。
2 结果与分析 2.1 三叉晶界迁移过程图 2为环形晶粒宽度w=14r0时三叉晶界的迁移过程。由图 2可见,在演化初期环形晶粒顶部的晶界曲率发生了部分变化(图 2a和b),之后晶界曲率保持稳定(图 2b~d)。这是因为初态的三叉晶界为不稳定状态(相邻晶界夹角不为120°),当相邻晶界夹角达到120°的稳态时,三叉晶界形状保持稳定。由于环形晶界曲率的驱动作用,环形晶粒顶部的弧形晶界不断向其曲率中心收缩(图 2a~d),直至三叉晶界消失,变成一条平直晶界(图 2e)。在整个演化过程中,晶界Ⅱ和晶界Ⅲ中平直晶界始终保持平直,说明三叉晶界迁移具有自相似性。从图 2还可见,3个晶粒的取向角度在演化过程中均保持不变,表明晶粒均未发生旋转。

|
(a)t=250 ts; (b)t=2 000 ts; (c)t=12 000 ts; (d)t=26 000 ts; (e)t=43 000 ts 图 2 三叉晶界的演化过程(w=14r0) Fig.2 The evolution process of a triple junction at w=14r0 |
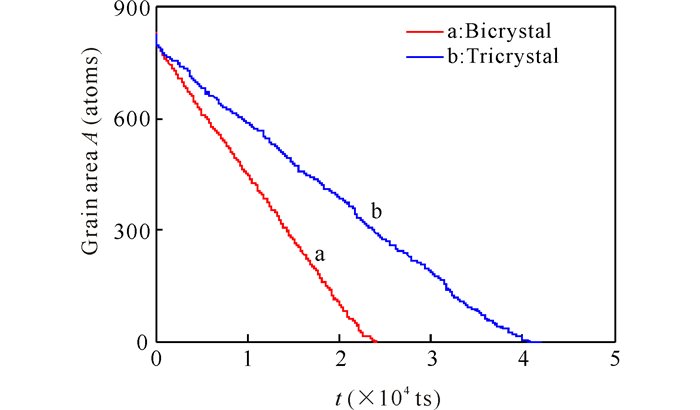
为了研究三叉晶界对晶界运动的影响,将图 1中晶粒b1和b2的取向角度取相同值(都为22.5°),则系统变为双晶系统(无三叉晶界)。双晶和三晶系统的晶界运动分别为晶界迁移和三叉晶界迁移。在相同条件下,双晶和三晶系统中环形晶粒面积A与演化时间t的关系曲线(A-t曲线)如图 3所示。可见,两种情况下A-t曲线均线性下降,其中三晶系统的下降速度明显小于双晶系统,可见前者的晶界迁移速率明显低于后者。这说明了三叉晶界对晶界迁移具有拖拽作用,与Czubayko等[3]和尹文红等[6]的实验结果吻合。
|
图 3 双晶和三晶系统中环形晶粒的面积与时间的关系(w=14r0) Fig.3 Curves between loop grain area A and time t in bicrystal and tricrystal system at w=14r0 |
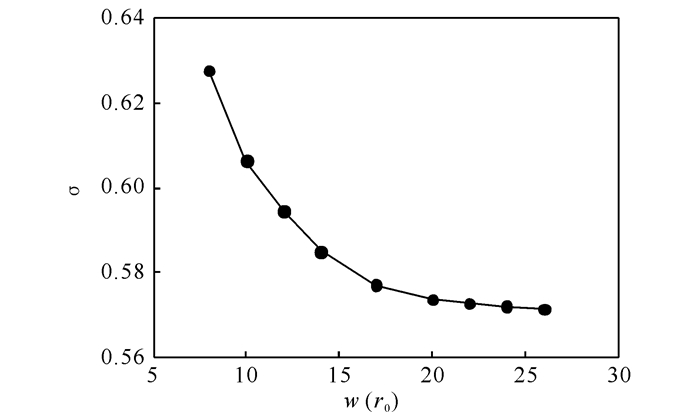
为了研究环形晶粒宽度w对三叉晶界拖曳作用的影响,环形晶粒宽度设为8r0≤w≤26r0,并计算A-t曲线的斜率,统计结果如图 4所示。图 4中纵坐标σ=ktj/kgb,其中ktj和kgb分别为三晶和双晶系统中A-t曲线的斜率。从图 4可见,w取不同值时,比值σ均小于1,且随着宽度w的增加,σ值不断减小。说明环形晶粒尺寸越大(晶界曲率越小),曲率驱动晶界迁移的速率越小,三叉晶界的拖拽作用就越明显。
|
图 4 斜率比σ(=ktj/kgb)与环形晶粒宽度w的关系 Fig.4 The curve between slop ratio σ(=ktj/kgb) and loop grain width w |
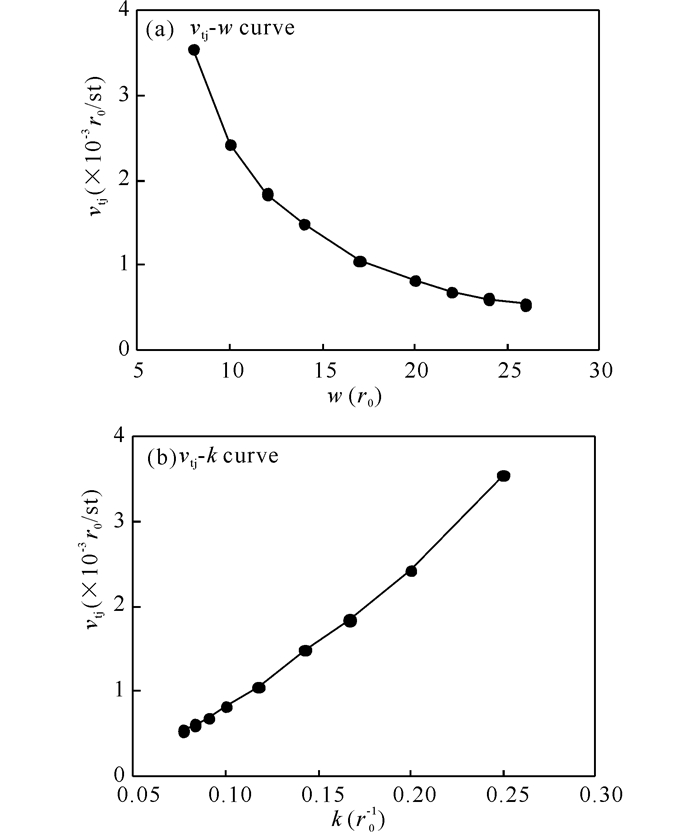
为了研究三叉晶界曲率对晶界迁移的影响,环形晶粒宽度设为8r0≤w≤26r0。从图 5a可见,随着环形晶粒宽度的增加,三叉晶界迁移速率不断减小。这是由于环形晶粒宽度越大,晶界迁移的驱动力就越小,导致晶界迁移越慢。由图 5b可见,随着晶界曲率k的增加,三叉晶界迁移速率vtj近似呈线性增加,表明三叉晶界迁移速率与晶界曲率成正比。该结果与经典晶界迁移理论[23]吻合。
|
图 5 三叉晶界迁移速率vtj与环形晶粒宽度w及其晶界曲率k的关系 Fig.5 Curves between migration rate vtj of triple junction and loop grain width w, and its grain boundary curvature k |
本研究采用PFC方法研究了将一个环形晶粒嵌入到双晶系统中三叉晶界的迁移过程,讨论了晶界曲率对三叉晶界迁移的影响。得到如下结论:1)在演化过程中,三叉晶界迁移具有自相似性,未发生晶粒旋转现象。2)晶界曲率影响三叉晶界迁移速率,并且两者成正比关系。3)三叉晶界对晶界迁移有拖曳作用,晶界曲率越小,三叉晶界的拖拽作用越明显。
| [1] |
FROLOV T, MISHIN Y. Molecular dynamics modeling of self-diffusion along a triple junction[J]. Physical Review B, 2009, 79(17): 174110. DOI:10.1103/PhysRevB.79.174110 |
| [2] |
GOTTSTEIN G, SHVINDLERMAN L S, ZHAO B. Thermodynamics and kinetics of grain boundary triple junctions in metals:Recent developments[J]. Scripta Materialia, 2010, 62(12): 914-917. DOI:10.1016/j.scriptamat.2010.03.017 |
| [3] |
CZUBAYKO U, SURSAEVA V G, GOTTSTEIN G, et al. Influence of triple junctions on grain boundary motion[J]. Acta Materialia, 1998, 46(16): 5863-5871. DOI:10.1016/S1359-6454(98)00241-9 |
| [4] |
PROTASOVA S G, GOTTSTEIN G, MOLODOV D A, et al. Triple junction motion in aluminum tricrystals[J]. Acta Materialia, 2001, 49(13): 2519-2525. DOI:10.1016/S1359-6454(01)00142-2 |
| [5] |
MATTISSEN D, MOLODOV D A, SHVINDLERMAN L S, et al. Drag effect of triple junctions on grain boundary and grain growth kinetics in aluminium[J]. Acta Materialia, 2005, 53(7): 2049-2057. DOI:10.1016/j.actamat.2005.01.016 |
| [6] |
尹文红, 王卫国, 方晓英, 等. 轧制变形量对高纯铝三叉晶界、晶界形变及退火行为的影响[J]. 上海大学学报:自然科学版, 2017, 23(3): 414-421. YIN W H, WANG W G, FANG X Y, et al. Effect of cold rolling reduction on deformation and annealing behavior of triple junctions and grain boundaries in high-purity aluminum[J]. Journal of Shanghai University:Natural Science, 2017, 23(3): 414-421. |
| [7] |
UPMANYU M, SROLOVITZ D J, SHVINDLERMAN L S, et al. Triple junction mobility:A molecular dynamics study[J]. Interface Science, 1999, 7(3): 307-319. |
| [8] |
TRAUTT Z T, MISHIN Y. Capillary-driven grain boundary motion and grain rotation in a tricrystal:A molecular dynamics study[J]. Acta Materialia, 2014, 65: 19-31. DOI:10.1016/j.actamat.2013.11.059 |
| [9] |
RAPAPORT D C. The art of molecular dynamics simulation[M]. 2nd ed. Cambridge: Cambridge University Press, 2004.
|
| [10] |
ELDER K, KATAKOWSKI M, HAATAJA M, et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88(24): 245701. DOI:10.1103/PhysRevLett.88.245701 |
| [11] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5): 51605. DOI:10.1103/PhysRevE.70.051605 |
| [12] |
TANG S, WANG J C, SVENDSEN B, et al. Competitive bcc and fcc crystal nucleation from non-equilibrium liquids studied by phase-field crystal simulation[J]. Acta Materialia, 2017, 139: 196-204. DOI:10.1016/j.actamat.2017.08.015 |
| [13] |
SCHMIEDEBERG M, ACHIM C V, HIELSCHER J, et al. Dislocation-free growth of quasicrystals from two seeds due to additional phasonic degrees of freedom[J]. Physical Review E, 2017, 96(1): 12602. DOI:10.1103/PhysRevE.96.012602 |
| [14] |
GAO Y J, HUANG L L, DENG Q Q, et al. Phase field crystal simulation of dislocation configuration evolution in dynamic recovery in two dimensions[J]. Acta Materialia, 2016, 117: 238-251. DOI:10.1016/j.actamat.2016.06.021 |
| [15] |
GAO Y, DENG Q, HUANG L, et al. Atomistic modeling for mechanism of crack cleavage extension on nano-scale[J]. Computational Materials Science, 2017, 130: 64-75. DOI:10.1016/j.commatsci.2017.01.003 |
| [16] |
毛鸿, 罗志荣, 黄世叶, 等. 材料裂纹扩展分叉机理的晶体相场法研究[J]. 广西科学, 2015, 22(5): 499-505. MAO H, LUO Z R, HUANG S Y, et al. Phase-field-crystal modeling for crack propagation and branch of materials[J]. Guangxi Sciences, 2015, 22(5): 499-505. |
| [17] |
卢昱江, 孔令一, 邓芊芊, 等. 微裂纹起裂扩展机理的晶体相场模拟[J]. 广西科学院学报, 2017, 33(4): 240-245. LU Y J, KONG L Y, DENG Q Q, et al. Phase field crystal simulation of nucleation and propagation of micro-cracks[J]. Journal of Guangxi Academy of Sciences, 2017, 33(4): 240-245. |
| [18] |
CHEN C, CHEN Z, ZHANG J, et al. Phase-field crystal modeling of shape transition of strained islands in heteroepitaxy[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(11): 2042-2048. DOI:10.1007/s11433-012-4896-1 |
| [19] |
黄礼琳, 华平, 王玉玲, 等. 凸曲率衬底外延生长界面演化的晶体相场模拟[J]. 广西科学, 2014, 21(3): 241-246. HUANG L L, HUA P, WANG Y L, et al. Simulation of epitaxial growth interface on convex substrate using phase field crystal method[J]. Guangxi Sciences, 2014, 21(3): 241-246. |
| [20] |
WU K A, VOORHEES P W. Phase field crystal simulations of nanocrystalline grain growth in two dimensions[J]. Acta Materialia, 2012, 60(1): 407-419. DOI:10.1016/j.actamat.2011.09.035 |
| [21] |
MCREYNOLDS K, WU K A, VOORHEES P. Grain growth and grain translation in crystals[J]. Acta Materialia, 2016, 120: 264-272. DOI:10.1016/j.actamat.2016.08.056 |
| [22] |
CHENG M W, WARREN J A. An efficient algorithm for solving the phase field crystal model[J]. Journal of Computational Physics, 2008, 227(12): 6241-6248. DOI:10.1016/j.jcp.2008.03.012 |
| [23] |
SUTTON A P, BALLUFFI R W. Interfaces in crystalline materials[M]. Oxford: Oxford University Press, 1995.
|
 2017, Vol. 24
2017, Vol. 24 


