2. 广西相对论天体物理重点实验室,广西南宁 530004
2. Guangxi Key Laboratory for the Relativistic Astrophysics, Guangxi University, Nanning, Guangxi, 530004, China
【研究意义】我国已经成为世界汽车大国,由于道路交通系统控制不完善和大量汽车出行导致交通拥堵的发生,降低了城市交通的通行能力。交通问题成为大中城市的社会问题,许多学者和工程师都为提高交通能力做出了不同的解决方案,从交通网络的重新规划建设到现有交通网络的优化控制及交通诱导和交通流建模等各个方面进行研究,为城市智能化的发展提供了理论,并促进有效控制城市道路交通拥堵,为人们出行带来方便,同时降低能源消耗减少空气污染。【前人研究进展】交通流的拥堵问题是当前科学研究的重点,许多学者为此提出了不同的交通流模型,其中微观的模型有跟驰模型、元胞自动机模型[1-5],介观模型有Boltzmann模型[6]等,以及宏观的流体力学模型[7-8]和格子流体力学模型[9-12]。宏观模型将交通流中的车辆假设为可压缩流体介质,将交通中的车辆位置和速度变量转化成流体的平均密度ρ和平均速度v对交通流的动力学行为进行描述。1955年,Lighthill和Whitham[7]在《论运动学波》发表了交通流宏观理论,在该理论中利用流体力学的质量守恒的连续性方程,同时假设车流速度与密度满足平衡速密关系,构成了交通流流体力学模型。并且Richards[8]也独立地提出了该理论,人们将其统称为LWR模型。由于在实际中,车流经历弛豫时间才达到平衡,而LWR模型车流的速度总是处于一个平衡状态或瞬间就达到平衡状态,这个过程不符合实际交通。在1969年,Payne[13]通过将Newell[14]提出的跟驰模型进行宏观转化得到了交通流高阶动力学模型来取代LWR模型中的平衡速密关系,并且与交通流连续性方程构成了交通流高阶动力学模型。然而实际交通中交通波的传播不等于车速,要求高阶连续性方程的特征速度小于或等于车速,即实际交通具有各向异性的特性。1995年Daganzo[15]指出Payne模型具有各向同性,干扰波的传播速度大于车速,后车会影响前车的行驶。为了解决交通流动力学的各向异性问题,2000年,Aw和Rascle[16]通过修改密度梯度项,提出了首个各向异性的高阶动力学模型,2002年Zhang[17]将微观跟驰模型进行宏观化,导出了新的各向异性的宏观方程。Jiang等[18]根据全速度差模型推导出各向异性的宏观动力学模型, 以速度梯度取代Payne模型的密度梯度项。Xue等[19]考虑了车流通过弛豫时间和驾驶员反应时间达到平衡,得出平衡速密关系,导出新的动力学模型。交通流各向异性的高阶流体力学模型具有各向异性的特性,而且解决了交通流车辆类气体倒退的问题。【本研究切入点】根据优化速度模型提出具有延迟效应的速度差反馈控制模型, 通过宏观化, 导出新的各向异性的交通流宏观动力学方程, 研究在宏观层面上具有延迟效应的交通流宏观的动力学行为, 同时研究延迟效应对交通拥堵的影响。【拟解决的关键问题】基于延迟效应速度差反馈控制模型推导出高阶流体力学模型, 在具有延迟效应的控制作用下抑制交通拥堵。
1 模型建立基于时间延迟的速度差优化速度模型为
| $ \frac{{{\rm{d}}{v_j}\left( t \right)}}{{{\rm{d}}t}} = a\left( {V\left( {\Delta {x_j}\left( t \right)} \right) - {v_j}\left( t \right)} \right) + \lambda \left( {{v_{j + 1}}\left( t \right) - {v_j}\left( {t - {T_d}} \right)} \right), $ | (1) |
其中Td表示延迟时间,λ是反是反馈控制增益。在方程(1) 中,将微观的车间距离转换成密度的宏观量可表示为
| $ {v_j}\left( t \right) \to v\left( {x,t} \right),{v_{j + 1}}\left( t \right) \to v\left( {x + \Delta ,t} \right),V\left( {\frac{1}{\rho }} \right) = {V_e}\left( \rho \right), $ |
| $ V'\left( {\frac{1}{\rho }} \right) = - {\rho ^2}{{V'}_e}\left( \rho \right),a = \frac{1}{T},\lambda = \frac{1}{\tau }, $ |
其中T表示车辆的弛豫时间,τ表示车辆在行驶Δ距离消耗的时间。那么对于微观方程(1) 式等式左侧可以转化为
| $ {v_{j + 1}}\left( t \right) = v\left( {x,t} \right) + \Delta {\partial _x}v + \frac{{{\Delta ^2}}}{2}\partial _x^2v, $ |
| $ {v_j} = \left( {t - {T_d}} \right) = v\left( {x,t} \right) - {T_d}{\partial _t}v + \frac{{T_d^2}}{2}\partial _t^2v。$ |
将上式相关量都代入到微观方程(1) 后化简,得到如下宏观动力学方程:
| $ \begin{array}{l} \;\;\;\;\;\;\frac{{\partial v}}{{\partial t}} + \frac{{\left( {v - {c_0}} \right)}}{\alpha }\frac{{\partial v}}{{\partial x}} = \frac{{\left( {{V_e}\left( \rho \right) - {v_j}\left( t \right)} \right)}}{{\alpha T}} + \frac{{{\Delta ^2}}}{{2\tau \alpha }}\partial _x^2v - \\ \frac{{T_d^2}}{{2\tau \alpha }}\partial _t^2v + \frac{1}{{\alpha T}}\left( {\frac{{{\rho _x}}}{{2\rho }} + \frac{{{\rho _{xx}}}}{{6{\rho ^2}}}} \right){{V'}_e}\left( \rho \right)。\end{array} $ | (2) |
而交通流满足如下连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho v} \right)}}{{\partial x}} = 0。$ | (3) |
因此,考虑了时间延迟效应的交通流宏观流体力学模型由方程(2) 和(3) 组成。其中
| $ {Q_t} + A\left( Q \right){Q_x} = E, $ | (4) |
其中上式中的量可表示为
| $ Q = \left[ {\begin{array}{*{20}{c}} \rho \\ v \end{array}} \right], $ |
方程组的系数矩阵可表示为
| $ A\left( Q \right) = \left( {\begin{array}{*{20}{c}} v&\rho \\ 0&{\frac{{v - {c_0}}}{\alpha }} \end{array}} \right), $ |
等式右边的矩阵表达为
| $ \begin{array}{l} E = \\ \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{{\left( {{V_e}\left( \rho \right) - {v_j}\left( t \right)} \right)}}{{\alpha T}} + \frac{{{\Delta ^2}}}{{2\tau \alpha }}\partial _x^2v - \frac{{T_d^2}}{{2\tau \alpha }}\partial _t^2v + \frac{1}{{\alpha T}}\left( {\frac{{{\rho _x}}}{{2\rho }} + \frac{{{\rho _{xx}}}}{{6{\rho ^2}}}} \right){{V'}_e}\left( \rho \right)} \end{array}} \right], \end{array} $ |
为了求解出方程组的特征值,那么系数矩阵满足特征方程:|A(Q)-λI|=0,该行列式的特征解为
| $ {\lambda _1} = v,{\lambda _2} = \frac{{v - {c_0}}}{\alpha }。$ |
从特征值可以明确地看出系统扰动传播的特征速度各不相同,均小于或者等于车速,那么考虑了延迟效应的交通流宏观模型具有各向异性的特性。
2 线性稳定性分析在初始状态交通流的密度和速度都加入一个小扰动,则其扰动的形式可表示为
| $ \left( \begin{array}{l} \rho \left( {x,t} \right)\\ v\left( {x,t} \right) \end{array} \right) = \left( \begin{array}{l} {\rho _0}\\ {v_0} \end{array} \right) + \sum\limits_k {\left( \begin{array}{l} {{\hat \rho }_k}\\ {{\hat v}_k} \end{array} \right)\exp \left( {ikx + {\sigma _k}t} \right)} 。$ | (5) |
将式(5) 分别代入到方程(3) 和(2) 中,那么模型的微扰方程的形式在简化后分别得到:
| $ \left( {{\sigma _k}t + ik{v_0}} \right){{\hat \rho }_k} + ik{\rho _0}{{\hat v}_k} = 0, $ | (6) |
| $ \begin{array}{l} {{\hat v}_k}{\sigma _k} + \frac{{\left( {{v_0} - {c_0}} \right)}}{\alpha }{{\hat v}_k}ik = \frac{{{{\hat \rho }_k}{{V'}_e}\left( {{\rho _0}} \right) - {{\hat v}_k}}}{{\alpha T}} + \frac{{{\Delta ^2}}}{{2\tau \alpha }}\\ {\left( {ik} \right)^2}{{\hat v}_k} + \chi , \end{array} $ | (7) |
其中
| $ \begin{array}{l} \left( {{\sigma _k} + \frac{{{v_0} - {c_0}}}{\alpha }ik} \right)\left( {{\sigma _k} + ik{v_0}} \right) = \frac{{ - ik{\rho _0}{{V'}_e}\left( {{\rho _0}} \right)}}{{\alpha T}} - \\ \frac{{\left( {{\sigma _k} + ik{v_0}} \right)}}{{\alpha T}} + \frac{{{\Delta ^2}}}{{2\tau \alpha }}\left( {{}^ik} \right)2\left( {{\sigma _k} + ik{v_0}} \right) - \\ \frac{{T_d^2}}{{2\tau \alpha }}\sigma _k^2\left( {{\sigma _k} + ik{v_0}} \right) - \frac{{ik{\rho _0}}}{{\alpha T}}\left( {\frac{{ik}}{{2{\rho _0}}} + \frac{{{{\left( {ik} \right)}^2}}}{{4\rho _0^2}}} \right){{V'}_e}\left( {{\rho _0}} \right)。\end{array} $ | (8) |
为确定方程(8) 中σk的取值,需要将其以ik的幂级数展开为σk=σ1ik+σ2(ik)2+…,为了简化计算,σk的幂级数展开到二阶项后代入到方程(8) 中,可进一步化简为
| $ \begin{array}{l} \left( {\frac{{{\rho _0}{{V'}_e}\left( {{\rho _0}} \right)}}{{\alpha T}} + \frac{{{\sigma _1} + {v_0}}}{{\alpha T}}} \right)ik + \left( {\sigma _1^2 + \frac{{\left( {{v_0} - {c_0}} \right)}}{\alpha }{\sigma _1} + } \right.\\ \left. {{\sigma _1}{v_0} + \frac{{\left( {{v_0} - {c_0}} \right)}}{\alpha }{v_0} + \frac{{{\sigma _2}}}{{\alpha T}} + \frac{{{{V'}_e}\left( {{\rho _0}} \right)}}{{2\alpha T}}} \right)\left( {{}^ik} \right)2 = 0。\end{array} $ | (9) |
为了使上式成立,幂级数中的一阶项ik和二阶项(ik)2前的指数都为0,那么可得如下方程组:
| $ \frac{{{\rho _0}{{V'}_e}\left( {{\rho _0}} \right)}}{{\alpha T}} + \frac{{{\sigma _1} + {v_0}}}{{\alpha T}} = 0, $ | (10) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\sigma _1^2 + \frac{{{v_0} - {c_0}}}{\alpha }{\sigma _1} + {\sigma _1}{v_0} + \frac{{{v_0} - {c_0}}}{\alpha }{v_0} + \frac{{{\sigma _2}}}{{\alpha T}} + \\ \frac{{{{V'}_e}\left( {{\rho _0}} \right)}}{{2\alpha T}} = 0。\end{array} $ | (11) |
联立方程(10) 和(11) 可解得σ1和σ2的值如下:
| $ {\sigma _1} = - {v_0} - {\rho _0}{{V'}_e}\left( {{\rho _0}} \right), $ |
| $ {\sigma _2} = \frac{{\left( { - \alpha {v_0} - \alpha {\rho _0}{{V'}_e}\left( {{\rho _0}} \right) + {v_0} + {c_0}} \right){\rho _0}}}{a} - \frac{1}{2}。$ |
为了使系统处于稳定状态,要求σ2>0,求得系统的稳定性条件为
| $ 2{\rho _0} = \left( {{v_0} + {c_0} - \alpha {v_0} - \alpha {\rho _0}{{V'}_e}\left( {{\rho _0}} \right)} \right) > a。$ | (12) |
已经求解出σ1和σ2,便可以确定σk的实部和虚部分别表示如下:
| $ \begin{array}{l} \mathit{Re}\left( {{\sigma _k}} \right) \approx \left( {\frac{{\left( {\alpha {v_0} + \alpha {\rho _0}{{V'}_e}\left( {{\rho _0}} \right) - {v_0} - {c_0}} \right){\rho _0}}}{a} + } \right.\\ \left. {\frac{1}{2}} \right){k^2} - O\left( {{k^4}} \right),\\ \mathit{Im}\left( {{\sigma _k}} \right) \approx - \left( {{\rho _0}{{V'}_e}\left( {{\rho _0}} \right) + {v_0}} \right)k + O\left( {{k^3}} \right)。\end{array} $ | (13) |
从(13) 式中显示出小扰动的传播临界速度c(ρ0)为c(ρ0)=ρ0V′e(ρ0)+v0,与文献[18]的传播速度相同。
3 非线性分析对交通系统引入一个新的坐标系,该坐标转换[22]为如下形式:
| $ z = x - ct。$ | (14) |
那么由上式的变换,可得关于坐标位置和时间的变量为x=z+ct,t=(x-z)/c。将方程(14) 代入到方程(3) 和(2) 中分别得到如下转换的方程式:
| $ - c{\rho _z} + {q_z} = 0, $ | (15) |
| $ \begin{array}{l} \;\;\;\;\;\; - c{v_z} + v{v_z} = \frac{{\left( {{V_e}\left( \rho \right) - v} \right)}}{{\alpha T}} + \frac{{{\Delta ^2}{v_{zz}}}}{{2\tau \alpha }} - \frac{{T_d^2{v_{zz}}}}{{2\tau \alpha }} + \\ \frac{{{{V'}_e}\left( \rho \right)}}{{\alpha T}}\left( {\frac{{{\rho _z}}}{{2\rho }} + \frac{{{\rho _{zz}}}}{{6{\rho ^2}}}} \right)。\end{array} $ | (16) |
由于交通流流量定义为交通流的密度与流速的乘积q=ρv,如果交通流流量以稳定态时的流量作泰勒展开,取到二阶项,则得:q=ρVe(ρ)+b1ρz+b2ρzz。将流量定义式代入到方程(15) 式中可求得交通流流速对变量z作一阶导数和二阶导数如下表示:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;{v_z} = \frac{{c{\rho _z}}}{\rho } - \frac{{q{\rho _z}}}{{{\rho ^2}}},{v_{zz}} = c{\rho ^{ - 1}}{\rho _{zz}} - c{\rho ^{ - 2}}\rho _z^2 - q{\rho ^{ - 2}}{\rho _{zz}} + \\ 2q{\rho ^{ - 3}}\rho _z^2。\end{array} $ |
将流量的泰勒展开式和交通流流速的一阶导数和二阶导数代入到方程(16) 中可得:
| $ \begin{array}{l} \;\;\;\;\;\;\left( { - {c^2} + 2{V_e}\left( \rho \right)c - V_e^2\left( \rho \right) + \frac{{{b_1}}}{{\alpha T}} - \frac{{{{V'}_e}\left( \rho \right)}}{{\alpha T}}} \right){\rho _z} + \\ \left[ {\frac{{{b_2}}}{{\alpha T}} - \frac{{{{V'}_e}\left( \rho \right)}}{{6\rho \alpha T}} - \left( {\frac{{{\Delta ^2}}}{{2\tau \alpha }} - \frac{{T_d^2}}{{2\tau \alpha }}} \right)c + \left( {\frac{{{\Delta ^2}}}{{2\tau \alpha }} - \frac{{T_d^2}}{{2\tau \alpha }}} \right){V_e}\left( \rho \right)} \right]{\rho _{zz}} = 0。\end{array} $ | (17) |
由于ρz和ρzz都不为零,那么等式(17) 式中ρz和ρzz前面的系数为零,那么就可以得到如下方程组:
| $ \left\{ \begin{array}{l} - {c^2} + 2{V_e}\left( \rho \right)c - V_e^2\left( \rho \right) + \frac{{{b_1}}}{{\alpha T}} - \frac{{{{V'}_e}\left( \rho \right)}}{{2\alpha T}} = 0\\ \frac{{{b_2}}}{{\alpha T}} - \frac{{{{V'}_e}\left( \rho \right)}}{{6\rho \alpha T}} - \left( {\frac{{{\Delta ^2}}}{{2\tau \alpha }} - \frac{{T_d^2}}{{2\tau \alpha }}} \right)c + \left( {\frac{{{\Delta ^2}}}{{2\tau \alpha }} - } \right.\\ \left. {\;\;\;\;\;\;\;\;\frac{{T_d^2}}{{2\tau \alpha }}} \right){V_e}\left( \rho \right) = 0 \end{array} \right.。$ | (18) |
解方程组(18) 可得b1和b2的值为
| $ \left\{ \begin{array}{l} {b_1} = \alpha T{c^2} - 2{V_e}\left( \rho \right)c\alpha T + \alpha TV_e^2\left( \rho \right) + \frac{{{{V'}_e}\left( \rho \right)}}{2}\\ {b_2} = \frac{{{{V'}_e}\left( \rho \right)}}{{6\rho }} + \left( {\frac{{{\Delta ^2}}}{{2\tau \alpha }} - \frac{{T_d^2}}{{2\tau \alpha }}} \right)c\alpha T - \left( {\frac{{{\Delta ^2}}}{{2\tau \alpha }} - } \right.\\ \left. {\;\;\;\;\;\;\;\;\frac{{T_d^2}}{{2\tau \alpha }}} \right){V_e}\left( \rho \right)\alpha T \end{array} \right.。$ |
密度可表示为稳定态密度ρ0与微扰
| $ \begin{array}{l} \;\;\;\;\;\;\rho {V_e}\left( \rho \right) \approx {\rho _0}{V_e}\left( {{\rho _0}} \right) + {\left( {\rho {V_e}} \right)_\rho }\left| {_{\rho = {\rho _0}}} \right.\hat \rho + \\ \frac{1}{2}{\left( {\rho {V_e}} \right)_{\rho \rho }}\left| {_{\rho = {\rho _0}}} \right.{{\hat \rho }^2}。\end{array} $ | (19) |
将方程(19) 代入到流量展开式中q=ρVe(ρ)+b1ρz+b2ρzz,并将流量展开式代入到(15) 式时,得:
| $ \begin{array}{l} \;\;\;\;\;\;\;\; - c{\rho _z} + \left( {{{\left( {\rho {V_e}} \right)}_\rho }\left| {_{\rho = {\rho _0}}} \right. + {{\left( {\rho {V_e}} \right)}_{\rho \rho }}\left| {_{\rho = {\rho _0}}} \right.\rho } \right){\rho _z} + {b_1}{\rho _{zz}} + \\ {b_2}{\rho _{zzz}} = 0。\end{array} $ | (20) |
为了将方程(20) 转换为KdV-Burgers方程,需要做相应坐标转换,则令X=mx,T=-mt。同时令U表示为
| $ \begin{array}{l} \;\;\;\;U = - \left( {{{\left( {\rho {V_e}} \right)}_\rho }\left| {_{\rho = {\rho _0}}} \right. + {{\left( {\rho {V_e}} \right)}_{\rho \rho }}\left| {_{\rho = {\rho _0}}} \right.\rho } \right) = \\ - \left[ {{{\left( {\rho {V_e}} \right)}_\rho } + {{\left( {\rho {V_e}} \right)}_{\rho \rho }}\rho } \right]。\end{array} $ | (21) |
在已知(21) 式后,可求得如下关于密度,及密度的导数各个相关量,表示如下:
| $ \begin{array}{l} \rho = \frac{{ - {{\left( {\rho {V_e}} \right)}_\rho }}}{{{{\left( {\rho {V_e}} \right)}_{\rho \rho }}}} - \frac{U}{{{{\left( {\rho {V_e}} \right)}_{\rho \rho }}}},{\rho _z} = - \frac{{m{U_T}}}{{c{{\left( {\rho {V_e}} \right)}_{\rho \rho }}}},\\ {\rho _z} = - \frac{{m{U_X}}}{{{{\left( {\rho {V_e}} \right)}_{\rho \rho }}}},{\rho _{zz}} = - \frac{{{m^2}{U_{XX}}}}{{{{\left( {\rho {V_e}} \right)}_{\rho \rho }}}},\\ {\rho _{zzz}} = - \frac{{{m^3}{U_{XXX}}}}{{{{\left( {\rho {V_e}} \right)}_{\rho \rho }}}}。\end{array} $ |
将以上相关量代入到(20) 式中,化简后得到KdV-Burgers方程如下:
| $ {U_T} + U{U_X} + {m_1}{U_{XX}} + {m_2}{U_{XXX}} = 0, $ |
其中有m1=-b1m,m2=-b2m2,那么对于标准的KdV-Burgers方程,其中的一个解为
| $ U = - \frac{{3m_1^2}}{{25{m_2}}}{\left[ {1 + \tan \mathit{h}\left( { \pm \frac{{{m_1}}}{{10{m^2}}}} \right)\left( {X + \frac{{6m_1^2}}{{25{m_2}}}T + {\xi _0}} \right)} \right]^2}, $ |
其中ξ0表示任意常数。密度波解可表示为
| $ \rho = \frac{{3m_1^2}}{{25{m_2}{{\left( {\rho {V_e}} \right)}_{\rho \rho }}}}{\left[ {1 + \tan \mathit{h}\left( { \pm \frac{{{m_1}}}{{10{m^2}}}} \right)\left( {X + \frac{{6m_1^2}}{{25{m_2}}}T + {\xi _0}} \right)} \right]^2} - \frac{{{{\left( {\rho {V_e}} \right)}_\rho }}}{{{{\left( {\rho {V_e}} \right)}_{\rho \rho }}}}。$ |
对于考虑了延迟效应的速度差模型推导出的相应的宏观模型,模拟在不同的密度下,研究系统的交通流密度的变化情况。对于方程(2) 和(3),设定其模拟的初始条件可表示为
| $ a = 0.1,L = 32.2{\rm{km}},\Delta x = 100,\Delta t = 1,\Delta {\rho _0} = 0.01,{c_0} = 10。$ |
初始密度值采用Herrmann和Kerner[23]提出的平均密度函数可表示为
| $ \begin{array}{l} \;\;\;\;\;\;\rho \left( {x,0} \right) = {\rho _0} + \Delta {\rho _0}\left\{ {\cos {\mathit{h}^{ - 2}}\left[ {\frac{{160}}{L}\left( {x - \frac{{5L}}{{16}}} \right)} \right] - } \right.\\ \left. {\frac{1}{4}\cos {\mathit{h}^{ - 2}}\left[ {\frac{{40}}{L}\left( {x - \frac{{11L}}{{32}}} \right)} \right]} \right\}。\end{array} $ |
采用Kerner和Konhäuser[24]提出的优化速度-密度函数可表示为
| $ \begin{array}{l} \;\;\;\;\;\;\;{V_e}\left( \rho \right) = \\ {v_f}\left[ {{{\left( {1 + \exp \frac{{\rho /{\rho _m} - 0.25}}{{0.06}}} \right)}^{ - 1}} - 3.72 \times {{10}^{ - 6}}} \right]。\end{array} $ |
优化速度-密度函数其相应的一阶导数经过求解可得:
| $ {{V'}_e}\left( \rho \right) = - \frac{{1/{\rho _m}}}{{0.06}}{v_f}{\left( {1 + \exp \frac{{\rho /{\rho _m} - 0.25}}{{0.06}}} \right)^{ - 2}}\exp \frac{{\rho /{\rho _m} - 0.25}}{{0.06}}。$ |
将以上的初始状态的所有条件代入到模型中,同时需要对模型进行相应的离散。研究中对偏微分方程采用了迎风格式离散模型。对于模型的连续性方程(3),离散格式为
| $ \rho _j^{i + 1} = \rho _j^i + \frac{{\Delta t}}{{\Delta x}}\rho _j^i\left( {v_j^i - v_{j + 1}^i} \right) + \frac{{\Delta t}}{{\Delta x}}v_j^i\left( {\rho _{j - 1}^i - \rho _j^i} \right)。$ | (22) |
当vji<c0时, 模型方程(2) 可采用向前差分格式,具体表示如下:
| $ \begin{array}{l} \;\;\;\;\;\;v_j^{i + 1} = \frac{{v_j^i}}{A} - \Delta t\frac{{\left( {v_j^i - {c_0}} \right)}}{\alpha }\frac{{v_{j + 1}^i - v_j^i}}{{A\Delta x}} + \\ \frac{{\Delta t\left( {{V_e}\left( {\rho _j^i} \right) - v_j^i} \right)}}{{A\alpha T}} + \frac{{\Delta t{\Delta ^2}}}{{2A\tau \alpha }}\frac{{v_{j + 1}^i - 2v_j^i + v_{j - 1}^i}}{{{{\left( {\Delta x} \right)}^2}}} - \\ \frac{{T_d^2}}{{2A\tau \alpha }}\frac{{\left( {v_j^{i - 1} - 2v_j^i} \right)}}{{\Delta t}} + \frac{{\Delta t{{V'}_e}\left( {\rho _j^i} \right)}}{{A\alpha T}}\left( {\frac{{\rho _{j + 1}^i - \rho _j^i}}{{2\rho _j^i\Delta x}} + } \right.\\ \left. {\frac{{\rho _{j + 1}^i - 2\rho _j^i + \rho _{j - 1}^i}}{{6{{\left( {\rho _j^i} \right)}^2}{{\left( {\Delta x} \right)}^2}}}} \right)。\end{array} $ | (23) |
当vji>c0时, 模型方程(2) 采用了向后差分格式,表示如下:
| $ \begin{array}{l} \;\;\;\;\;\;v_j^{i + 1} = \frac{{v_j^i}}{A} - \Delta t\frac{{\left( {v_j^i - {c_0}} \right)}}{\alpha }\frac{{v_j^i - v_{j - 1}^i}}{{A\Delta x}} + \\ \frac{{\Delta t\left( {{V_e}\left( {\rho _j^i} \right) - v_j^i} \right)}}{{A\alpha T}} + \frac{{\Delta t{\Delta ^2}}}{{2A\tau \alpha }}\frac{{v_{j + 1}^i - 2v_j^i + v_{j - 1}^i}}{{{{\left( {\Delta x} \right)}^2}}} - \\ \frac{{T_d^2}}{{2A\tau \alpha }}\frac{{\left( {v_j^{i - 1} - 2v_j^i} \right)}}{{\Delta t}} + \frac{{\Delta t{{V'}_e}\left( {\rho _j^i} \right)}}{{A\alpha T}}\left( {\frac{{\rho _{j + 1}^i - \rho _j^i}}{{2\rho _j^i\Delta x}} + } \right.\\ \left. {\frac{{\rho _{j + 1}^i - 2\rho _j^i + \rho _{j - 1}^i}}{{6{{\left( {\rho _j^i} \right)}^2}{{\left( {\Delta x} \right)}^2}}}} \right), \end{array} $ | (24) |
其中
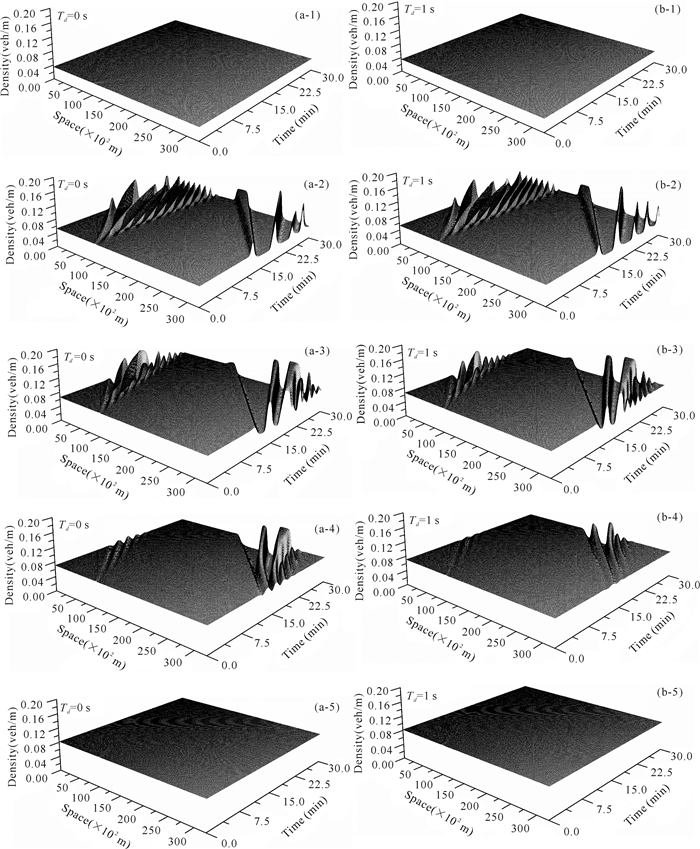
图 1a-1到图 1a-5延迟时间Td为0 s,稳定态的密度ρ0的取值分别为0.035 veh/m,0.053 veh/m,0.066 veh/m,0.071 veh/m,0.082 veh/m。在不同的稳定态密度的情况下,图 1a-1和图 1a-5在运行时系统都处于一个稳定的状态,表明宏观系统中,低密度和高密度的状态下,系统是稳定的。而在模拟的数据中,0.035 veh/m<ρ0<0.071 veh/m时,系统在运行中将会出现交通拥堵,形成时停时走的交通状态。
|
图 1 交通流在不同延迟时间和初始密度下的时间演化图 Fig.1 Temporal evolution of traffic with different delay time and initial density |
图 1b-1到图 1b-5延迟时间Td为1 s,且稳定态的密度ρ0取值分别对应于图 1a-1到图 1a-5中的密度。和图 1a-1和图 1a-5的情况类似,在低密度和高密度状态下,系统在演变过程中都是稳定的。在初始稳态密度为0.035 veh/m<ρ0<0.071 veh/m时,道路还是会出现相应的时停时走的状态,但是相较于图 1a-4,图 1b-4所形成的不稳定状态范围在缩小,表明系统稳定状态的范围在扩大,因此延迟效应下的宏观模型更有利于系统的稳定。
5 结论本研究对具有延迟效应的速度差反馈控制方程进行宏观化得到相应的高阶动力学方程, 同时为了使交通流系统方程闭合, 引入了守恒连续性方程。然后, 对高阶宏观流体力学方程进行了线性稳定性分析, 得出系统的稳定性条件。通过非线性分析, 导出描述密度波的KdV-Burgers方程, 并给出相应的密度波解。在数值模拟中采用了迎风格式离散模型, 研究在不同的延迟时间和密度下系统的成簇效应和系统稳定性, 研究发现考虑延迟时间后, 成簇效应的密度范围相应缩小, 系统的稳定性区域得到了进一步的扩大, 表明了时间延迟效应有利于交通流系统的稳定。
| [1] |
CHOWDHURY D, SANTEN L, SCHADSCHNEIDER A, et al. Statistical physics of vehicular traffic and some related systems[J]. Phys Rep, 2000, 329(4/6): 199-329. |
| [2] |
HELBING D. Traffic and related self-driven many-particle systems[J]. Rev Mod Phys, 2001, 73(4): 1067-1141. DOI:10.1103/RevModPhys.73.1067 |
| [3] |
KERNER B S. The physics of traffic[M]. Berlin Heidelberg: Springer, 2004.
|
| [4] |
盘薇, 贾丽斯, 薛郁. 信号灯随机更新的城市交通网络模型[J]. 广西科学, 2016, 23(3): 189-193. PAN W, JIA S L, XUE Y. Signal controlled urban traffic network model with random update rule[J]. Guangxi Sciences, 2016, 23(3): 189-193. |
| [5] |
贾丽斯, 盘薇, 陈栋, 等. 交通瓶颈处局域密度时间序列的长程相关性[J]. 广西科学, 2016, 23(3): 216-222. JIA S L, PAN W, CHEN D, et al. Long-range correlation analysis of time series at traffic bottleneck[J]. Guangxi Sciences, 2016, 23(3): 216-222. |
| [6] |
PRIGOGINE I, ANDREWS F C. A Boltzmann-like approach for traffic flow[J]. Operations Research, 1960, 8(6): 789-797. DOI:10.1287/opre.8.6.789 |
| [7] |
LIGHTHILL M J, WHITHAM G B. On kinematic waves.I.Flood movement in long rivers[J]. Proc Roy Soc A Math Phys Eng Sci, 1955, 299(1178): 281-345. |
| [8] |
RICHARDS P I. Shock waves on the highway[J]. Operations Research, 1956, 4(1): 42-51. DOI:10.1287/opre.4.1.42 |
| [9] |
NAGATANI T. Modified KdV equation for jamming transition in the continuum models of traffic[J]. Physica A:Statistical Mechanics and Its Applications, 1998, 261(3/4): 599-607. |
| [10] |
NAGATANI T. TDGL and MKdV equations for jam-ming transition in the lattice models of traffic[J]. Physica A:Statistical Mechanics and Its Applications, 1999, 264(3/4): 581-592. |
| [11] |
薛郁. 优化车流的交通流格子模型[J]. 物理学报, 2004, 53(1): 25-30. XUE Y. Lattice models of the optimal traffic current[J]. Acta Physica Sinica, 2004, 53(1): 25-30. DOI:10.7498/aps.53.25 |
| [12] |
李瑞鑫, 郭言, 薛郁. 基于格子流体力学模型的交通拥堵反[J]. 广西科学, 2016, 23(3): 206-211-211. LI R X, GUO Y, XUE Y. Comparison of feedback control schemes for traffic jam based on lattice hydrodynamic traffic model[J]. Guangxi Sciences, 2016, 23(3): 206-211-211. |
| [13] |
PAYNE H J.Models of freeway traffic and control [C]//BEKEY G A (ed.).Mathematical models of public systems.Proc.1971 SCI conference.Simulation Councils Proceedings Series, 1971, 1:51-61.
|
| [14] |
NEWELL G F. Nonlinear effects in the dynamics of car following[J]. Operations Research, 1961, 9(2): 209-229. DOI:10.1287/opre.9.2.209 |
| [15] |
DAGANZO C F. Requiem for second-order fluid approximations of traffic flow[J]. Transportation Research Part B:Methodological, 1995, 29(4): 277-286. DOI:10.1016/0191-2615(95)00007-Z |
| [16] |
AW A, RASCLE M. Resurrection of "second order" models of traffic flow[J]. SIAM J Appl Math, 2000, 60(3): 916-938. DOI:10.1137/S0036139997332099 |
| [17] |
ZHANG H M. A non-equilibrium traffic model devoid of gas-like behavior[J]. Transportation Research Part B:Methodological, 2002, 36(3): 275-290. DOI:10.1016/S0191-2615(00)00050-3 |
| [18] |
JIANG R, WU Q S, ZHU Z J. A new continuum model for traffic flow and numerical tests[J]. Transportation Research Part B:Methodological, 2002, 36(5): 405-419. DOI:10.1016/S0191-2615(01)00010-8 |
| [19] |
XUE Y, DAI S Q. Continuum traffic model with the consideration of two delay time scales[J]. Phys Rev E, 2003, 68(6): 066123-1. DOI:10.1103/PhysRevE.68.066123 |
| [20] |
BERG P, MASON A, WOODS A. Continuum approach to car-following models[J]. Phys Rev E, 2000, 61(2): 1056-1066. DOI:10.1103/PhysRevE.61.1056 |
| [21] |
LIU G Q, LYRINTZIS A, MICHALOPOULOS P. Improved high-order model for freeway traffic flow[J]. Transportation Research Record:Journal of the Transportation Research Board, 1998, 1644: 37-46. DOI:10.3141/1644-05 |
| [22] |
BERG P, WOODS A W. On-ramp simulations and solitary waves of a car-following model[J]. Phys Rev E, 2001, 64(3): 035602-1-035602-4. |
| [23] |
HERRMANN M, KERNER B S. Local cluster effect in different traffic flow models[J]. Physica A:Statistical Mechanics and Its Applications, 1998, 255(1/2): 163-188. |
| [24] |
KERNER B S, KONHÄUSER P. Cluster effect in initially homogeneous traffic flow[J]. Phys Rev E, 1993, 48(4): R2335-R2338. DOI:10.1103/PhysRevE.48.R2335 |
 2017, Vol. 24
2017, Vol. 24 


