2. 广西相对论天体物理重点实验室,广西南宁 530004
2. Guangxi Key Laboratory for the Relativistic Astrophysics, Guangxi University, Nanning, Guangxi, 530004, China
【研究意义】随着科学研究的发展,已经有许多学者研究和讨论同步现象及其相关问题,其范围涵盖了化学、物理、生物等自然科学和工程学、社会学行为等诸多领域,它们都与同步的基本性质关系密切。同步存在于大自然中各种自然发生的集体现象,正如我们发现的一些具体问题亦存在同步现象,如:约瑟夫森结[1]、纳米力学[2]、萤火虫的闪动[3]、心脏起搏器[4]、帕金森氏综合症[5]、反冲原子激光器[6]等。在研究中,同步的核心问题在于复杂系统,而复杂网络动力学系统中耦合振子的相位同步行为一直都是热门的研究话题之一。【前人研究进展】控制论奠基人Wiener最先开始研究集体同步行为,然而他使用的数学方法(基于傅里叶积分)被认为是不可行的。紧随着,Winfree给出了一个新的观点:将同步问题简化成相位变化的问题。日本学者Kuramoto基于Winfree的观点简化出一个包含N个性质几乎相同的极限环振子的耦合系统,其模型也成为了研究耦合振子相位同步的最经典的模型之一,动力学方程为
| $ {\dot \theta _i} = {w_i} + \frac{K}{N}\sum\nolimits_{j = 1}^N {\sin \left( {{\theta _j}-{\theta _i}} \right), i = 1, 2, \cdots, N, } $ | (1) |
其中θi表示第i个振子的相位, wi表示第i个振子瞬时相位的固有频率,K代表节点之间的耦合强度,其值大于0。虽然Kuramoto将方程进行了简化,但方程(1) 仍旧无法计算出解析解。Kuramoto利用平均场理论,假设振子之间为全局耦合,振子的固有频率wi通常满足一定的分布函数g(ω)(如高斯,洛伦兹分布等)且与它的平均频率Ω(t=0)=∑wi/N对称。为了能够直观刻画相位动力学,获得系统中振子之间相位的同步程度,引入序参量
| $ Z = \mathit{R}{\mathit{e}^{\mathit{i}\phi }} = \frac{1}{N}\sum\nolimits_{j = 1}^n {{e^{i{\theta _j}}}}, $ | (2) |
其中Z为复序参量,表征系统的有序程度;R用来描述系统的相干性,ϕ为序参量;为平均相位。随着时间的增加,当系统达到完全同步时(θi(t)=θj(t), ∀i, j∈1, …,N), R=1, 在热力学极限(N→∞)下,R=0, 而当振子没有达到同步时, 振子之间的相位无相干性。对于任意有限N,可以引入一个平均频率Ωi(对于所有i,
| $ {\mathit{\Omega }_i} = \left\langle {\dot \theta } \right\rangle = \frac{1}{T}\int_0^T {{{\dot \theta }_i}\left( t \right){\rm{d}}t, } $ | (3) |
其中〈·〉为时间平均,T为演化时间,dt为时间步长。当两个振子达到同步时,其平均频率相等,两个振子的相位差不随着时间变化,即达到锁相。通过同步分岔树[7]来理解系统的同步过程:随着耦合强度的增加,固有频率相近的振子会先行同步形成小集团,进而集团之间相互耦合达到同步,最终所有振子的平均频率均相等[8]。平均场Kuramoto模型被应用于局域耦合、振幅效应、非简谐耦合、混沌振子等研究,其中最被人熟知的就是局域耦合振子模型。
Zheng等[7]的研究处于无耦合作用下随机固有频率粒子的周期性运动状态,在不稳定锁相态出现时观察到了振子同步相位滑移和量化相位转变,通过增加耦合,分岔树出现从高维准周期到混乱再到高维准周期的周期现象,不同的混沌振子和混沌成簇相位同步的序参量在此结构中起着重要作用。Wu等[9]提出最近邻对称耦合的Kuramoto方程,发现在临界耦合强度Kc时发生同步的概率呈现对数正态分布,通过定义空间频率构型粗糙度(roughness)物理量,发现两种类型的同步,分别对应小粗糙度的多重成簇(multiple-clustering)同步和对应大粗糙度的单一中心成簇(single-center-clustering)同步。Ji等[10]论证了在一个二阶Kuramoto模型中的节点经过一系列转变趋向一个同步宏观状态,称之为成簇爆炸式同步。通过在无相关网络中使用平均场解析爆炸式同步机制,证实新发现与数值模拟结果一致,从根本上加深了对微观机制趋向同步的理解。Zhang等[11]提出了在一般复杂网络中存在的一个爆炸式同步框架。该框架中,假设振子耦合强度与振子固有频率正相关,先前的研究被包含在特例中。通过替换爆炸式同步的2个必要条件(无标度网络拓扑和振子固有频率与振子的度正相关),从根本上深入理解微观机制趋向同步。Zhu等[12]模拟了在加权静态网络中的Kuramoto模型,发现当网络边缘强度与一对振子两段频率差为线性相关时,微观相关指数β=1,度分布指数γ>3时为一阶相变,2<γ≤3时为二阶相变。还发现当微观相关指数β从正数变为负数时,在均匀网络(γ→∞)爆炸式同步会变成连续相变,该发现为理解爆炸性行为提供了一个新的研究角度。Huang等[13]证实了在弱局域耦合系统下长程相关性的存在。Li等[14]研究了含有一阶、二阶相互作用的Kuramoto模型,用振子相位分布特性来描述不同的吸引子,通过观察序参量、相分布的向前向后延长的转换图发现,单峰相分布的同步状态是最稳定的,均匀分布双峰相分布的成簇同步是最不稳定的。Ji等[15]研究拓扑对二阶Kuramoto振子组成的网络动力学的影响。根据无标度网络中的一些拓扑性质,提出了成簇爆炸式同步(Cluster Explosive Synchronization,CES),通过淬火无序研究了不连续转变的鲁棒性,得出相位相干性随淬火无序强度的增大而减小的结论。从根本上加深了对处于固有频率和局域结构关联的约束下拓扑和动力学之间相互作用的理解。黄霞等[8]提出单向最近邻环上非线性振子的动力学模型来研究单向耦合振子的动力学行为,发现在非对称耦合作用下频率分岔树同步区呈现多定态分支现象。Huang等[16]考虑在无标度网络中耦合相振子Kuramoto模型的爆炸式同步,假定振子固有频率与度相关且系统中含有位错,结果发现延迟同步现象,且相变类型也发生改变。基于星图的研究方法提出了一种自洽方法去研究延迟同步机制且在实验中可改变位错这一可控参量。【本研究切入点】在平均场Kuramoto模型的基础上,考虑非对称的局域耦合,同时考虑到次近邻振子来讨论系统动力学行为。【拟解决的关键问题】基于平均场的Kuramoto局域耦合振子模型,建立次近邻单向耦合非线性振子的动力学模型,探讨次近邻耦合振子动力学行为。
1 模型建立局域耦合中只考虑最近邻振子之间相互作用的动力学方程为[7]
| $ \dot \theta = {w_i} + \frac{K}{3}\left[{\sin \left( {{\theta _{i + 1}}-{\theta _i}} \right) + \sin \left( {{\theta _{i-1}}-{\theta _i}} \right)} \right], $ | (4) |
可以看到全局耦合振子平均场方程(1) 和最近邻耦合方程(4) 在周期边界条件下(θN+1=θ1, θN=θ0)都是左右对称耦合。
一维闭合环上Kuramoto相振子在非对称最近邻耦合作用下同步区域出现多定态现象,其动力学方程为[8]
| $ \dot \theta = {w_i} + 2K\sin \left( {{\theta _{i + 1}}-\theta } \right), i = 1, 2, \cdots, N。$ | (5) |
本研究讨论的是一维闭合环上次近邻Kuramoto相振子在非对耦合作用下的同步动力学行为,其模型可表示为
| $ \begin{array}{l} \;\;\;\;\dot \theta = {w_i} + 3K\left( {\sin \left( {{\theta _{i + 2}}-{\theta _i}} \right) + \sin \left( {{\theta _{i + 1}}-{\theta _i}} \right)} \right), i = \\ 1, 2, \cdots, N。\end{array} $ | (6) |
为了便于讨论,不失一般性,设所有振子的固有频率的平均值为0。如若固有频率的平均值不为0,可以将平均频率Ω作w的平移[17],使得系统整体行为特征保持不变。同时考虑周期性边界条件(θN+1=θ1, θN=θ0),使得形成的耦合振子系统是一个单向耦合环。
2 数值模拟首先对方程(3) 的宏观参量平均频率Ω进行分析,为了便于讨论,不失一般性,取所有振子的固有频率的平均值为0,定义每一个振子的固有频率wi在[-1, 1]随机取值,初始相位取[0, 2π]范围内任意值。分别选取振子数较少(N=6, 7) 和振子数较多(N=20, 50) 的耦合极限环系统数值模拟。
图 1为模拟N=6, N=7, N=20, N=50系统得到的平均频率Ω与振子耦合强度K的分岔树。对于N=6的系统,当耦合强度K从0慢慢开始增加时,6个振子的平均频率慢慢向中间靠拢,直到都汇聚到频率w=0上,产生同步现象,并且随着时间和耦合强度的增加不发生改变(图 1a)。在非同步区,虽然振子的初始相位不同,系统耦合强度不同,但对于所有不同N的系统,同步分岔树呈现单一的动力学状态,即具有遍历性。在同步区,图中均存在平均频率Ω=0的同步态,除此之外,系统中还存在其他的同步定态,即耦合振子系统在达到同步时出现了多个同步定态共存的现象(图 1b~d)。研究发现这一现象与振子固有频率的分布情况无关,当考虑振子的固有频率为其他分布(如Lorentz分布、高斯分布等)情况时,系统也会出现多定态分支现象[8]。通过比较文献[8],发现当考虑次近邻振子后,系统的临界耦合强度Kc值变小了,由此可知次近邻单向耦合振子对系统的同步行为有影响。

|
图 1 不同振子数系统平均频率Ω随耦合强度K变化的同步分岔树 Fig.1 Bifurcation trees of average frequency for different system sizes |
图 2考虑了与图 1对应系统的序参量R。随着耦合强度的增强,序参量R从非零值逐渐增加到1,系统从非同步态经历二级非平衡相变逐渐达到完全同步态。虽然初始时刻相位在[0,2π]随机取值,但对于同一耦合强度,最终结果只有一个对应的序参量R值(图 2a)。对于N>6系统,可以发现同步区域内除了存在R趋近于1这个分支外,还存在其他的分支,随着耦合强度的增加这些分支开始逐渐减小并趋向于0,即存在多个不同的同步态,而且随着系统的扩大,序参量R会越来越趋向于0(图 2b~d)。

|
图 2 不同振子数系统序参量R随耦合强度K变化的关系 Fig.2 The plots of R versus K for different systems sizes |
选取图 1和图 2中N=7的系统,并将图中相同区域放大,如图 3。在图 3中发现,对于平均频率不为0的定态分支, 其平均频率与耦合强度之间呈线性增加关系。同时发现当系统处于平均频率为0的定态分支时,序参量趋于1,而系统处于平均频率不为0的其他定态分支时,序参量向0趋近,可知此定态下振子的相位没有被锁定到相同值上。
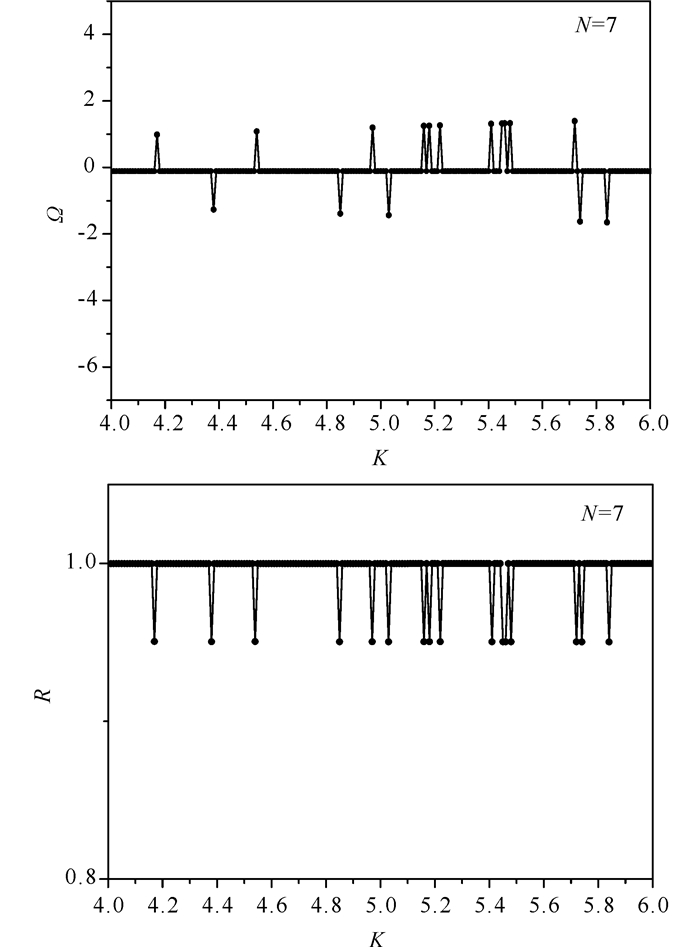
|
图 3 图 1(b)和图 2(b)的局部放大图 Fig.3 Partial enlarged plots of figure 1(b) and figure 2(b) |
通过数值模拟可知,当处于不同大小的系统状态时,系统中非线性振子的动力学行为就会有所不同。当N≤6时,系统达到同步单一同步态,当N>6时,系统就会出现多个不同的同步态。
3 理论分析和数值计算分析耦合振子较少的单向非对称耦合系统,对于N=3的单向耦合情形,引入相差ϕ1=θ2-θ1和ϕ2=θ3-θ2,得到如下相差方程:
| $ \begin{array}{l} {\phi _1} = \Delta {w_{21}} + 3K\left( {\sin {\phi _2}-2\sin {\phi _1}-\sin \left( {{\phi _1} + {\phi _2}} \right)} \right), \\ {\phi _2} = \Delta {w_{22}} + 3K\left( {\sin {\phi _1}-2\sin {\phi _2} - \sin \left( {{\phi _1} + {\phi _2}} \right)} \right), \end{array} $ | (7) |
其中Δw21=w2-w1,Δw22=w3-w2, 3个振子的固有频差为0,耦合强度取为2,从而保证系统满足同步条件。分析发现当耦合强度足够大时系统存在3个不动点,为(0,0),(0, π), (0, -π), 对于二维系统, 雅克比矩阵定义为
| $ I\left( \begin{array}{l} \frac{{\theta {{\dot \phi }_1}}}{{\theta {\phi _{}}1}}\;\;\frac{{\theta {{\dot \phi }_1}}}{{\theta {\phi _2}}}\\ \frac{{\theta {{\dot \phi }_2}}}{{\theta {\phi _1}}}\;\;\frac{{\theta {{\dot \phi }_2}}}{{\theta {\phi _2}}} \end{array} \right), $ |
则方程(7) 对应的雅可比矩阵为
| $ \begin{array}{l} \;\;I = \\ 3K\left( \begin{array}{l} -2\cos {\phi _1}-\cos \left( {{\phi _1} + {\phi _2}} \right)\;\;\;\;\cos {\phi _2}-\cos \left( {{\phi _1} + {\phi _2}} \right)\\ \;\;\;\cos {\phi _1} - \cos \left( {{\phi _1} + {\phi _2}} \right)\;\;\;\;\; - 2\cos {\phi _2} - \cos \left( {\phi 1 + {\phi _2}} \right) \end{array} \right)。\end{array} $ |
分析这些点的稳定性,对于(0,0) 不动点,其对应的本征值为λ=-3,由于本征值只有实部且小于0,该点是稳定结点,对于(0,±π),对应的本征值为λ1=-1, λ2=3,实部有大于0和小于0两种情况,根据非线性动力学可知,(0,±π)为不稳定鞍点,因此N=3系统不会出现多定态分支。通过理论分析发现,在少体系统中,同步区只存在单一同步态且序参量只有R=1这一条分支。
4 结论本研究利用Kuramoto局域耦合模型研究一维闭合环上次近邻单向耦合振子在非对称耦合作用下同步动力学行为,发现在单向耦合环上,非线性振子的频率分岔树同步区出现多定态分支现象,比较证明单向耦合次近邻振子对同步存在影响。理论分析了少体系统, 结果表明非零稳态出现分支现象与系统的大小有关。对于非同步区的动力学行为,由于较为复杂,我们将在今后的工作中做深入研究。
| [1] |
WIESENFELD K, COLET P, STROGATZ S H. Synch-ronization transitions in a disordered Josephson Series Array[J]. Physical Review Letters, 1996, 76(3): 404-407. DOI:10.1103/PhysRevLett.76.404 |
| [2] |
CROSS M C, ZUMDIECK A, LIFSHITZ R, et al. Synchronization by nonlinear frequency pulling[J]. Physical Review Letters, 2004, 93(22): 224101. DOI:10.1103/PhysRevLett.93.224101 |
| [3] |
ERMENTROUT B. An adaptive model for synchrony in the firefly Pteroptyx malaccae[J]. Journal of Mathematical Biology, 1991, 29(6): 571-585. DOI:10.1007/BF00164052 |
| [4] |
VINOGRADOVA T M, LYASHKOV A E, ZHU W Z, et al. High basal protein kinase A-dependent phosphorylation drives rhythmic internal Ca2+ store oscillations and spontaneous beating of cardiac pacemaker cells[J]. Circulation Research, 2006, 98(4): 505-514. DOI:10.1161/01.RES.0000204575.94040.d1 |
| [5] |
STAM C J. Nonlinear dynamical analysis of EEG and MEG:Review of an emerging field[J]. Clinical Neurophysiology, 2005, 116(10): 2266-2301. DOI:10.1016/j.clinph.2005.06.011 |
| [6] |
JAVALOYES J, PERRIN M, POLITI A. Collective atomic recoil laser as a synchronization transition[J]. Physical Review E, 2008, 78(1): 011108. DOI:10.1103/PhysRevE.78.011108 |
| [7] |
ZHENG Z G, HU G, HU B. Phase slips and phase synchronization of coupled oscillators[J]. Physical Review Letters, 1998, 81(24): 5318-5321. DOI:10.1103/PhysRevLett.81.5318 |
| [8] |
黄霞, 徐灿, 孙玉庭, 等. 耦合振子系统的多稳态同步分析[J]. 物理学报, 2015, 64(17): 170504. HUANG X, XU C, SUN Y T, et al. Multiple synchronous states in a ring of coupled phase oscillators[J]. Acta Physica Sinica, 2015, 64(17): 170504. DOI:10.7498/aps.64.170504 |
| [9] |
WU Y, XIAO J H, HU G, et al. Synchronizing large number of nonidentical oscillators with small coupling[J]. EPL (Europhysics Letters), 2012, 97(4): 40005. DOI:10.1209/0295-5075/97/40005 |
| [10] |
JI P, PERON T K, MENCK P J, et al. Cluster explosive synchronization in complex networks[J]. Physical Review Letters, 2013, 110(21): 218701. DOI:10.1103/PhysRevLett.110.218701 |
| [11] |
ZHANG X Y, HU X, KURTHS J, et al. Explosive synchronization in a general complex network[J]. Physical Review E, 2013, 88(1): 010802. DOI:10.1103/PhysRevE.88.010802 |
| [12] |
ZHU L H, TIAN L, SHI D N. Explosive transitions to synchronization in weighted static scale-free networks[J]. The European Physical Journal B, 2013, 86(11): 451. DOI:10.1140/epjb/e2013-40807-6 |
| [13] |
HUANG X, ZHAN M, LI F, et al. Single-clustering synchronization in a ring of Kuramoto oscillators[J]. Journal of Physics A:Mathematical and Theoretical, 2014, 47(12): 125101. DOI:10.1088/1751-8113/47/12/125101 |
| [14] |
LI K R, MA S, LI H H, et al. Transition to synchronization in a Kuramoto model with the first-and second-order interaction terms[J]. Physical Review E, 2014, 89(3): 032917. DOI:10.1103/PhysRevE.89.032917 |
| [15] |
JI P, PERON T K, RODRIGUES F A, et al. Analysis of cluster explosive synchronization in complex networks[J]. Physical Review E, 2014, 90(6): 062810. DOI:10.1103/PhysRevE.90.062810 |
| [16] |
HUANG X, GAO J, SUN Y T, et al. Effects of frustration on explosive synchronization[J]. Frontiers of Physics, 2016, 11(6): 110504. DOI:10.1007/s11467-016-0597-y |
| [17] |
MURUGANANDAM P, FERREIRA F F, ELNASH-AR H F, et al. Analytical calculation of the transition to complete phase synchronization in coupled oscillators[J]. Pramana, 2008, 70(6): 1143-1151. DOI:10.1007/s12043-008-0119-8 |
 2017, Vol. 24
2017, Vol. 24 


