【研究意义】牛鞭效应是供应链管理中的一个重要现象,这一现象表现为供应链中需求信息逐级放大并存在时间上的延迟。这种延迟使得上游企业对需求预测的准确率降低,因而造成库存的波动,引发企业运作成本增加和顾客满意度下降等一系列问题。【前人研究进展】为削弱牛鞭效应,国内外学者提出许多增强供应链系统稳定性的方法,如系统动力学、控制论、统计物理等[1-7]。这些方法从不同角度对供应链稳定性进行深入分析。目前,在这些方法中利用统计物理和非线性力学研究供应链系统稳定性非常活跃[3-23]。统计物理将供应链系统抽象为一个多粒子或多成分的系统。在这个系统中,供应链各节点间物料的流通存在一定的时间延迟,因而造成各级供应商库存的波动和系统的不稳定[8-19]。2004年,Nagatani和Helbing[16]将物料流与交通流理论中的车辆流进行类比,提出供应链物料守恒模型。该模型通过优化进货函数预测未来时刻的库存量,以此减少库存波动增强系统稳定性,从而降低牛鞭效应的影响。随后,Donner等[20]利用推方式(push)、拉方式(pull)及其两者混合策略预测系统库存,并对3种策略下的供应链稳定性进行分析。Konishi等[21]提出一种自适应调整策略来避免供应不足或过剩。【本研究切入点】上述策略在一定程度上都降低了牛鞭效应的影响,增强了系统的稳定性[4-22]。但是利用这些策略进行预测时不可避免地会出现一些误差,而这些误差在供应链中会被供应商逐级放大,进而导致系统库存大幅波动。因此,本研究从库存预测误差对供应链稳定性的影响着手,研究两种不同的预测策略及产生的误差对于供应链稳定性的影响。【拟解决的关键问题】首先给出线性稳定性分析,其次通过数值模拟,讨论基于库存的预测策略和基于需求市场的预测策略对系统稳定性的影响,最后基于上述结果对库存管理提供一些建议。
1 供应链模型在供应链中,每个企业在接受上游企业提供的原材料和半成品的同时,也在向下游企业供应自己的制成品。这些制成品对下游企业来讲,又是原料和半成品。为获得生存与发展,企业必须持续不断地从上游企业获得原材料和半成品等必需品,同时向下游企业输出本企业的制成品[3]。因此,本研究假定供应链系统内企业之间原材料的传输是连续的,其拓扑结构如图 1所示。供应商i从上游供应商i-1处获取商品,加工后并销往下游供应商i+1,其中Ni表示供应商i的库存量,λi表示第i个供应商从其上游第i-1个供应商得到的收货率,同时它也是第i-1个供应商给下游第i个供应商的发货率[4]。N0表示原材料,Nu+1表示市场需求。

|
图 1 线性供应链结构 Fig.1 Illustration of the linear supply chain |
在本研究中,考虑一个供应链由u个供应商组成,供应商的库存量Ni随时间变化并且满足下面的关系[3-19]:
| $ \frac{{{\rm{d}}{N_i}}}{{{\rm{d}}t}} = {\lambda _i}\left( t \right) - {\lambda _{i + 1}}\left( t \right)。$ | (1) |
假设在一定的延迟时间(自适应时间)T内,发货率的瞬时变化率与实际的发货率及期望的发货率之间的偏差成正比,即
| $ \frac{{{\rm{d}}{\lambda _i}}}{{{\rm{d}}t}} = \frac{1}{T}\left[ {{W_i}\left( t \right) - {\lambda _i}\left( t \right)} \right], $ | (2) |
Wi为期望订货率,随供应链中各级库存Ni的增加而减少。它在一定程度上反映各级供应商的订单管理策略。
为减少库存波动降低牛鞭效应,Nagatani和Helbing[16]提出具有预期效益的库存管理策略。该模型假定期望订货率不仅依赖于供应链节点当前的库存量,而且也依赖于库存量未来一段时间的变化量,即
| $ \begin{array}{l} \;\;\;\;\;\;\;\;{W_i}\left( t \right) = {W_i}\left( {\left\{ {{N_i}\left( t \right)} \right\},\left\{ {{\rm{d}}{N_j}\left( t \right)/{\rm{d}}t} \right\}} \right) = \\ W\left( {{N_{\left( i \right)}}\left( t \right)} \right), \end{array} $ | (3) |
其中N(i)(t)为现有库存量的预估值:
| $ {N_{\left( i \right)}}\left( t \right) = \sum\limits_{l = - n}^n {{c_l}\left( {{N_{i + l}} + \tau \frac{{{\rm{d}}{N_{i + l}}}}{{{\rm{d}}t}}} \right)} 。$ | (4) |
这种策略既考虑了供应商库存的当前状况以及未来一段时间内(τ)的预期变化,也考虑了其上下游供应商库存的当前状况和未来一段时间内的预期变化。该策略考虑的信息比较全面,在一定程度上增强了系统的稳定性。但是这种策略过于理想化,上下游供应链的库存量一般很难准确获取,并且未来一段时间库存的变化量也很难估计。
在实际中,供应链上的各级供应商对需求市场的变化并不敏感,或者信息沟通不畅使他们对需求市场的具体变化一无所知,各供应商往往根据经验对现有库存进行估计。在经济形势展望乐观情形下,库存估计值往往以一定比例增加;在经济形势展望悲观情形下,库存估计值往往以一定比例减小[1],即
| $ {N_{\left( i \right)}}\left( t \right) = {N_i}\left( t \right)\left( {1 + r} \right), $ | (5) |
其中r为估算比率。
此外,需求市场的任何变动都有可能造成生产过剩或不足。因此,供应商在估计自身库存量变化时往往会考虑供应链终端需求市场的变化。但是需求市场的变化传递到上游供应商时往往存在一定的延迟,并且在传递的过程中,这些信息会被逐级放大或扭曲。因此各供应商对于自身库存变化的估计,往往是供应链终端需求市场变化的几倍[24-26],即
| $ {N_{\left( i \right)}} = {N_i}\left( t \right) + K{E_{u + 1}}\left( t \right), $ | (6) |
其中Eu+1(t)为t时刻需求市场的变化;K为放大系数,衡量将需求市场变化量放大的程度。
对于上述两种策略(基于库存的预测策略和基于需求市场的预测策略),不管采用哪种策略,未来时刻的实际需求量与预测值之间总存在偏差εi,即
| $ {N_{\left( i \right)}} = {N_i}\left( t \right) + {\varepsilon _i}\left( t \right)。$ | (7) |
如果供应链各节点实时跟踪市场需求变化,并且能及时调整自身库存,也就是各供应商库存的变化量与供应链终端需求市场的变化量一致,即N(i)=Ni(t)+Eu+1(t),那么偏差εi=0,供应链整个库存就不会波动,系统处于恒稳态。
2 线性稳定性分析在恒稳态情况下,初始状态为Ni=N0,λi=λ0。假定δNi(t)和δλi(t)是系统的小扰动,与初始状态之间满足以下关系[16-19]:
| $ {N_i}\left( t \right) = {N_0} + \delta {N_i}\left( t \right), $ | (8) |
| $ {\lambda _i}\left( t \right) = {\lambda _0} + \delta {\lambda _i}\left( t \right)。$ | (9) |
将方程(8) 与(9) 代入方程(1)、(2) 和(5),可得系统的扰动方程:
| $ \frac{{{\rm{d}}\delta {N_i}\left( t \right)}}{{{\rm{d}}t}} = \delta {\lambda _i}\left( t \right) - \delta {\lambda _{i + 1}}\left( t \right), $ | (10) |
| $ T\frac{{{\rm{d}}\delta {\lambda _i}\left( t \right)}}{{{\rm{d}}t}} = W'\left( {{N_0}} \right)\left( {1 + r} \right)\delta {N_i}\left( t \right) - \delta {\lambda _i}\left( t \right), $ | (11) |
其中W′(N0)是期望订货函数在Ni=N0处的导数。
将δNi(t)=Xexp (iIk+zt)与δλi(t)=Yexp (iIk+zt)(其中
| $ zX = \left( {1 - {e^{Ik}}} \right)Y, $ | (12) |
| $ zTY = W'\left( {{N_0}} \right)\left( {1 + r} \right)X - Y。$ | (13) |
由此可以看出,当Ik→0, z→0时,z的首项是Ik的整数阶次幂。设z的长波形扩展为z=z1(Ik)+z2(Ik)2+z3(Ik)3+…,则通过方程(12) 与(13) 可得:
| $ {z_1} = - \left( {1 + r} \right)W'\left( {{N_0}} \right), $ | (14) |
| $ {z_2} = - z_1^2T - \frac{1}{2}W'\left( {{N_0}} \right)\left( {1 + r} \right)。$ | (15) |
如果z2<0,则对于长波长的模(对应于小的波数k的模),系统在平衡点是不稳定的;如果z2>0,系统在平衡点是稳定的。因此系统的稳定性条件为
| $ T < \frac{1}{{2\left( {1 + r} \right)\left| {W'\left( {{N_0}} \right)} \right|}}。$ | (16) |
当供应链的延迟时间T满足上述关系时,扰动对供应链影响甚微,系统是稳定的。当供应链的延迟时间T不满足上述关系时,扰动沿供应链向上下游传播,供应链系统不稳定。如图 2所示,稳定线曲线是供应链分配系统稳定区域与不稳定区域的分界,随着误差系数r的增大,曲线向下拓展,系统不稳定区域逐渐增大(Nc为系统库存临界点)。
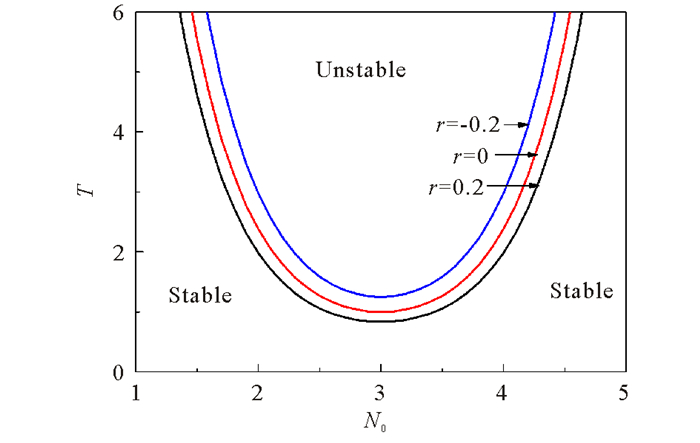
|
图 2 供应链稳定曲线(Nc=3) Fig.2 Stability curve of supply chain (Nc=3) |
对于基于需求市场的预测策略,我们同样进行线性稳定性分析,稳定性条件为
| $ T < \frac{1}{{2\left| {W'\left( {{N_0}} \right)} \right|}}, $ | (17) |
这与基于库存的预测策略结果类似,是公式(16) 中r=0的情形。
3 模拟与分析对方程(1) 和(2) 进行欧拉积分,时间步长选为Δt=0.01。为减小边界的影响,选取200个供应链节点。原材料的初始订货率为
| $ {\lambda _0} = W\left( {{N_0}} \right)。$ | (18) |
市场需求瞬息万变,设市场需求边界条件为
| $ {N_{u + 1}}\left( t \right) = {N_0} + {E_{u + 1}}\left( t \right) = {N_0} + \frac{{\xi \left( t \right)}}{2}, $ | (19) |
其中ξ(t)是白噪声,它满足<ξ(t)>=0和<ξ(t)ξ(t′)>=δtt′/4。
| $ W\left( {{N_{\left( i \right)}}} \right) = 1 - \left[ {\tanh \left( {{N_{\left( i \right)}} - {N_c}} \right) + \tanh \left( {{N_c}} \right)} \right]/2, $ | (20) |
这里Nc为系统库存临界点,在本研究中Nc=3。
3.1 预测误差对供应链稳定性的影响如果供应链各节点实时跟踪市场需求变化,并且能及时调整自身库存,也就是各供应商库存的变化量与供应链终端需求市场的变化量一致,即N(i)=Ni(t)+Eu+1(t),那么供应链整个库存就不会波动,系统处于恒稳态(图 3a)。但是一旦各供应商库存的变化量与需求市场的变化量不一致,出现预测误差(εi),那么供应链系统将失稳(图 3b、c)。靠近供应链需求市场的供应商,对市场需求变化的反应相对较快,误差带来的扰动容易被系统吸收,这些库存没有出现波动。而远离供应链需求市场的供应商,受到需求市场及其下游供应链库存误差的累积影响,使其库存出现较大幅度的波动,牛鞭效应明显。当误差较小时,靠近需求市场的供应链是稳定的,远离需求市场的供应链是不稳定的。随着误差的增大,供应商库存波动的数量增多,系统不稳定区域逐渐扩大。因此,完全消除牛鞭效应非常困难,但是采取必要的策略可以削弱牛鞭效应的影响范围,至少可以使系统达到部分稳态。
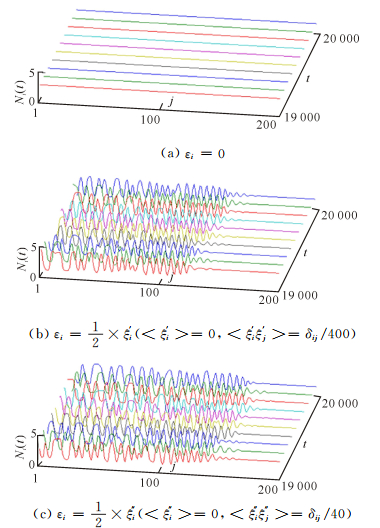
|
图 3 不同误差影响下供应链库存波动曲线(T=2,Nc=3) Fig.3 Inventory oscillation of supply chain under different errors (T=2, Nc=3) |
此外,考虑供应链库存波动随延迟时间(自适应时间)的变化。从图 4可以看出,供应链库存波动出现在延迟时间T=1.2时。随后随着延迟时间的增大,系统库存波动开始大幅增大。对比不同误差范围下的库存波动,两者基本一致,只是在临界点附近出现偏差。结合图 3和图 4不难发现,误差大小仅仅影响供应链稳定区域供应商的数量,对不稳定区域库存幅度的变化影响不大。
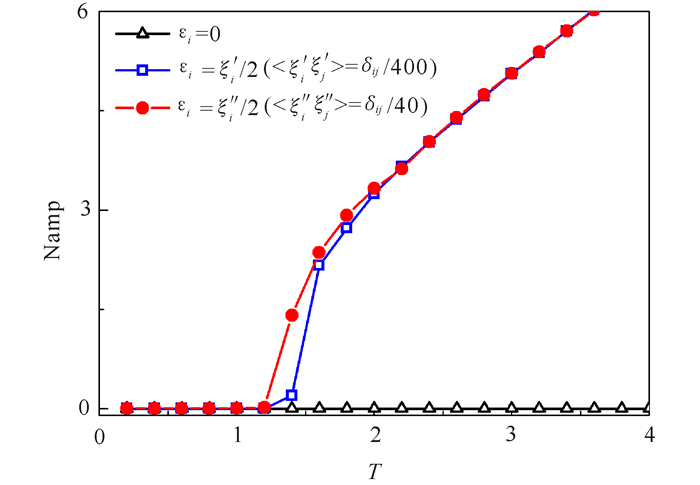
|
图 4 不同误差影响下供应链库存波动幅度随延迟时间的变化 Fig.4 Amplitude variation of supply chain inventory with delay time under different errors |
在实际中,供应链上各级供应商对市场需求的变化并不敏感,或者信息沟通不畅使他们对市场需求具体变化一无所知,他们往往根据经验对现有库存进行粗略估计,或增大或减小一定比例[1],即N(i)=(1+r)Ni(t)。在经济形势展望乐观情形下,他们会增大库存(r>0),因此相应的预测值就会偏大;在经济形势展望悲观情形下,他们会减小库存(r<0),因此相应的预测值就会偏小。在这种情况下,预测误差εi=(1+r)Ni(t)-(Ni(t)+Eu+1)=rNi(t)-Eu+1。
图 5给出不同估算比率下供应商库存的变化情况,临界点出现在r=-0.4。当估算比率r<-0.4时,供应商都在试图减产,库存量减少使得系统供不应求,各供应商的库存量不会出现波动,系统处于稳定状态。但是随着估算比率r的增大,预测的误差值随之增大,库存量预测值增多使得生产过剩,库存开始出现波动,系统处于不稳定状态。在线性稳定性分析中,稳定性曲线将系统分为稳定和不稳定区域;而在模拟中,随着估算比率的增大,系统由稳定状态转变为不稳定状态,两者结论基本一致。
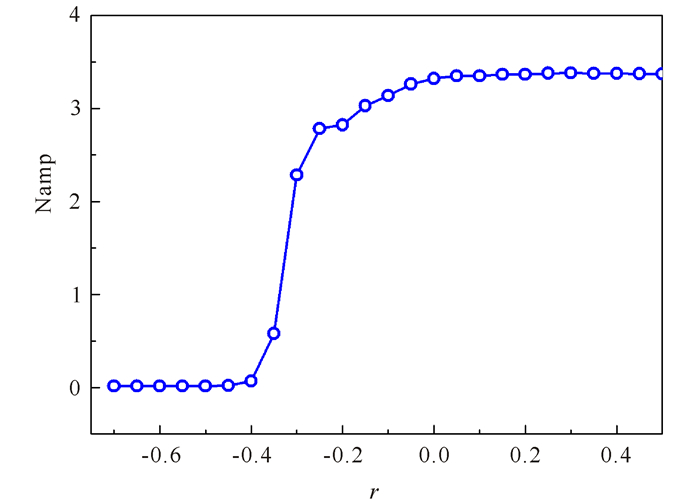
|
图 5 供应链库存波动幅度随估算比率的变化 Fig.5 Amplitude variation of supply chain inventory with estimated ratio |
同样地,当延迟时间较小时,供应商对需求市场的反应迅速,各供应商库存量波动容易被系统吸收,系统处于稳定状态。随着延迟时间的增大,库存波动随延迟时间大幅增大。对比不同的估算比率,变化趋势基本一致,只是在临界点出现差异(图 6)。当估算比率r=0.2时,临界点出现在T=1附近;当估算比率r=-0.2时,临界点出现在T=1.4附近。这说明适当降低估算比率可以增强系统的稳定性。
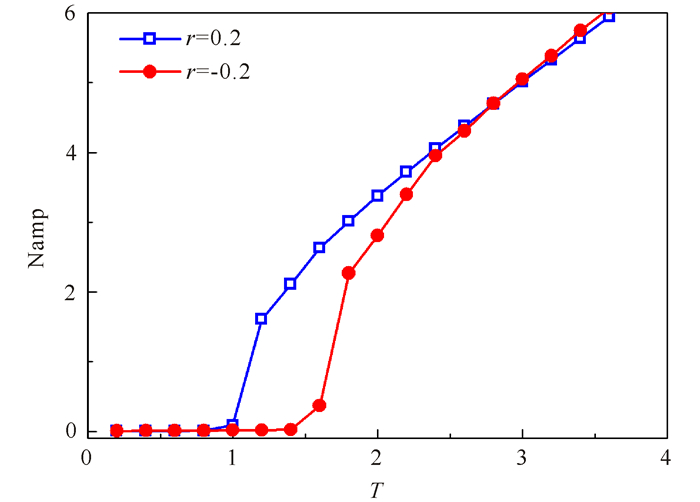
|
图 6 基于库存的预测策略下供应链库存波动幅度随延迟时间的变化 Fig.6 Amplitude variation of supply chain inventory with the delay time in varied inventory forecasting strategy |
市场需求的变化传递到上游供应商时往往存在一定的延迟,并且在传递的过程中,这些信息会被逐级放大或扭曲。因此各供应商对于自身库存变化的预测,往往是供应链末端需求市场变化的几倍[27],即N(i)=Ni(t)+KEu+1(t)。因此预测误差在这种情况下变为εi=(K-1)Eu+1(t)。当K=1时,各供应商库存的变化量与需求市场变化量一致,系统处于恒稳态。
如图 7所示,当K<10时,各供应商对库存变化的估计值相对较小,低库存量无法满足市场的需求,系统处于不稳态。当K>10时,各供应商对库存变化的估计值相对较大,高库存量可以消除需求市场波动产生的扰动,系统转为稳态。由此可见,根据需求市场的变化量对于供应商库存的估计值越大,系统越容易达到稳态。但是这种稳态造成的后果是库存量过大,容易造成生产过剩, 引发企业运作成本增加。这一结论与牛鞭效应结论吻合。值得注意的是,随着放大系数的增大,这种策略下库存的预测误差随之增大,但是系统却趋向稳定。导致这一现象的原因在于牛鞭效应,需求市场的变化信息在传递的过程中被放大或扭曲,高库存降低了预测误差对于系统稳定性的影响。这也是在实际中供应商普遍采用高库存降低供应链波动的动机所在。
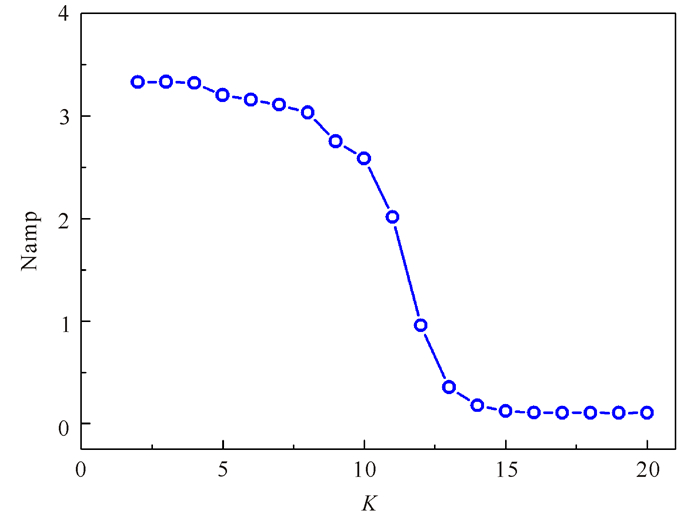
|
图 7 供应链库存波动幅度随放大率的变化 Fig.7 Amplitude variation of supply chain inventory with magnification |
类似地,由图 8可知供应链库存波动的临界点出现在T=1.4附近。随着延迟时间的增大,库存波动随延迟时间大幅增大。对比不同放大率的情形,供应链库存波动幅度基本一致,只是在临界点附近出现偏差。在临界点附近,高放大率下的供应链库存波动幅度低于低放大率下的情形。这就说明增大放大率,可以提高系统的稳定性,这与图 7结论一致。
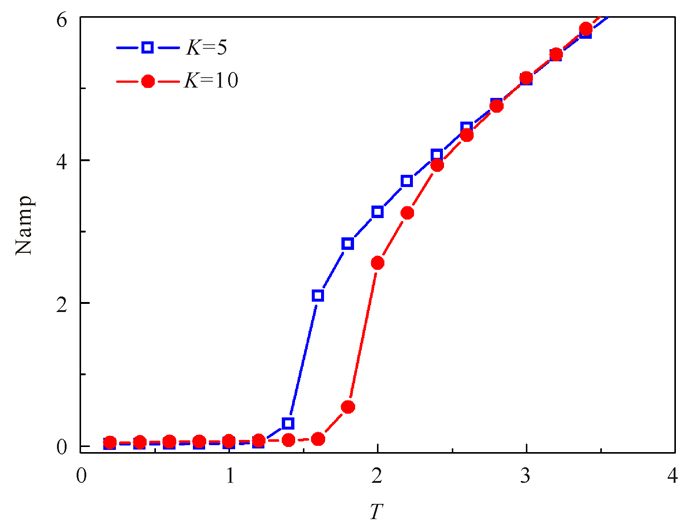
|
图 8 基于需求市场的预测策略下供应链库存波动幅度随延迟时间的变化 Fig.8 Amplitude variation of supply chain inventory with the delay time in varied demand market forecasting strategy |
本研究从预测误差角度出发,探讨两种预测策略对供应链系统稳定性的影响。运用线性稳定性分析,得出系统的稳定与不稳定区域。在此基础上,通过数值模拟分别讨论基于库存的预测策略和基于需求市场的预测策略及其误差对供应链稳定性的影响。基于库存自身进行预测,可以减小误差降低库存波动,增强系统稳定性,这与理论分析结果一致。基于需求市场进行预测时,由于牛鞭效应的存在,误差在传递过程中被放大或扭曲,高库存量降低了预测误差的影响,保障了供应链系统的稳定性。另外,对于两种策略,减少系统延迟时间均可以减小市场需求波动产生的扰动,增强系统的稳定性。
| [1] |
SARIMVEIS H, PATRINOS P, TARANTILIS C D, et al. Dynamic modeling and control of supply chain systems:A review[J]. Comput Oper Res, 2008, 35(11): 3530-3561. DOI:10.1016/j.cor.2007.01.017 |
| [2] |
郭进利. 供应链型网络中双幂律分布模型[J]. 物理学报, 2006, 55(8): 3916-3921. GUO J L. The bilateral power-law distribution model of supply chain networks[J]. Acta Physica Sinica, 2006, 55(8): 3916-3921. DOI:10.7498/aps.55.3916 |
| [3] |
黄健, 陈国华, 肖条军, 等. 一类复杂供应链网络的稳定性分析[J]. 中国管理科学, 2005, 13(S1): 298-301. HUANG J, CHEN G H, XIAO T J, et al. Stability analysis of a type of complex supply chain networks[J]. Chinese Journal of Management Science, 2005, 13(S1): 298-301. |
| [4] |
周海磊, 郝杨杨, 林国龙, 等. 运用Matlab的线性供应链仿真控制策略研究[J]. 数学的实践与认识, 2015, 45(18): 62-71. ZHOU H L, HAO Y Y, LIN G L, et al. The simulation control strategies research of linear supply chain used in Matlab[J]. Mathematics in Practice and Theory, 2015, 45(18): 62-71. |
| [5] |
JIA S L, WANG L, LUO C.The research on stability of supply chain under variable delay based on system dynamics[M]//RENKO S (ed.).Supply chain management-new perspectives.Rijeka, Croatia:InTech, 2011.
|
| [6] |
RABELO L, SARMIENTO A T, JONES A, et al. Stability of the supply chain using system dynamics simulation and the accumulated deviations from equilibrium[J]. Modelling and Simulation in Engineering, 2011, 2011: 603632. |
| [7] |
ZONG G Q, JI S W. Study on the stability of supply chain system based on production decision[J]. Applied Mechanics and Materials, 2014, 635/637: 1789-1793. DOI:10.4028/www.scientific.net/AMM.635-637 |
| [8] |
LI Z H, CHEN Y, CHEN X Q. Stability analysis of supply chain system based on E-commerce[J]. Advanced Materials Research, 2011, 171/172: 783-786. |
| [9] |
WANG J H, WANG P H. Using control theory to explore the Bullwhip effect in the supply chain for a deteriorating product[J]. International Journal of Electronic Business Management, 2005, 3(1): 8-16. |
| [10] |
BRAY R L, MENDELSON H. Information transmiss-ion and the Bullwhip effect:An empirical investigation[J]. Management Science, 2012, 58(5): 860-875. DOI:10.1287/mnsc.1110.1467 |
| [11] |
LP W H, CHAN S L, LAM C Y. Modeling supply chain performance and stability[J]. Industrial Management & Data Systems, 2011, 111(8): 1332-1354. |
| [12] |
WANG H S, JIA S L. Impact of echelon ratio for the Bullwhip effect in a three-echelon supply chain based on multi-agent simulation[J]. Journal of Computers, 2013, 8(10): 2598-2606. |
| [13] |
FU D F, DUTTA A, IONESCU C M, et al. Reducing the Bullwhip effect in supply chain management by applying a model predictive control ordering policy[J]. IFAC Proceedings Volumes, 2012, 45(6): 481-486. DOI:10.3182/20120523-3-RO-2023.00075 |
| [14] |
DAI J H, PENG S B, LI S B. Mitigation of Bullwhip effect in supply chain inventory management model[J]. Procedia Engineering, 2017, 174: 1229-1234. DOI:10.1016/j.proeng.2017.01.291 |
| [15] |
HELBING D, LÄMMER S, SEIDEL T, et al. Physics, stability, and dynamics of supply networks[J]. Phys Rev E, 2004, 70(6): 066116. DOI:10.1103/PhysRevE.70.066116 |
| [16] |
NAGATANI T, HELBING D. Stability analysis and stabilization strategies for linear supply chains[J]. Physica A:Statistical Mechanics and Its Applications, 2004, 335(3/4): 644-660. |
| [17] |
HELBING D. Modelling supply networks and business cycles as unstable transport phenomena[J]. New J Phys, 2003, 5(1): 90. |
| [18] |
NAGATANI T. Dynamical transition in random supply chain[J]. Physica A:Statistical Mechanics and Its Applications, 2004, 335(3/4): 661-670. |
| [19] |
NAGATANI T. Stability and transition in multiple production lines[J]. Physica A:Statistical Mechanics and Its Applications, 2004, 334(1/2): 243-254. |
| [20] |
DONNER R, PADBERG K, HOFENER J, et al. Progress in industrial mathematics at ECMI 2008[M]. Berlin Heidelberg: Springer, 2010: 527.
|
| [21] |
KONISHI K. A tuning strategy to avoid blocking and starving in a buffered production line[J]. Eur J Oper Res, 2010, 200(2): 616-620. DOI:10.1016/j.ejor.2009.01.032 |
| [22] |
KASTSIAN D, MÖNNIGMANN M. Optimization of a vendor managed inventory supply chain with guaranteed stability and robustness[J]. Int J Prod Econom, 2011, 131(2): 727-735. DOI:10.1016/j.ijpe.2011.02.022 |
| [23] |
KRISTIANTO Y, HELO P, JIAO J X, et al. Adaptive fuzzy vendor managed inventory control for mitigating the Bullwhip effect in supply chains[J]. Eur J Oper Res, 2012, 216(2): 346-355. DOI:10.1016/j.ejor.2011.07.051 |
| [24] |
BECKER T, BEBER M E, WINDT K, et al. Flow control by periodic devices:A unifying language for the description of traffic, production, and metabolic systems[J]. J Stat Mech, 2011(5): 05004. |
| [25] |
HE H D, LU W Z, XUE Y, et al. Dynamic characteristics and simulation of traffic flow with slope[J]. Chin Phys B, 2009, 18(7): 2703-2708. DOI:10.1088/1674-1056/18/7/013 |
| [26] |
DEJONCKHEERE J, DISNEY S M, LAMBRECHT M R, et al. Measuring and avoiding the Bullwhip effect:A control theoretic approach[J]. Eur J Oper Res, 2003, 147(3): 567-590. DOI:10.1016/S0377-2217(02)00369-7 |
| [27] |
HOBERG K, BRADLEY J R, THONEMANN U W. Analyzing the effect of the inventory policy on order and inventory variability with linear control theory[J]. Eur J Oper Res, 2007, 176(3): 1620-1642. DOI:10.1016/j.ejor.2005.10.040 |
 2017, Vol. 24
2017, Vol. 24 


