2. 沧州职业技术学院,河北 沧州 061000
2. Vocational and Technical College of Cangzhou, Cangzhou, Hebei, 061000, China
【研究意义】随着科技的高速发展,电子芯片等微小型元器件的功率和热量大幅度增加,热量的淤积会影响电子芯片的功能,因此需要设计合理的换热装置及时移除多余热量。热沉作为一种高效的传热装置常用于电子芯片等元器件。自Tuckerman和Pease[1]首次提出微通道热沉,便吸引了大量国内外学者的关注。【前人研究进展】 Wu等[2-3]研究了平直微通道热沉的传热和流动特性,发现微细通道热沉能有效进行散热。夏国栋等[4]和唐慧敏等[5]期望改进微细通道的结构形式以提高其传热能力。从热力学角度看,热量传递过程是一个不可逆过程,会导致有用能损失。为了分析有用能损失的情况,Bejan[6-7]基于热力学第二定律提出熵产概念。熵产数揭示了对流换热过程的物理本质,被多数研究者用于评价微细通道的对流换热性能,并以最小熵产原理来优化传热过程[8-10]。已有研究表明,在弯曲通道内由弯曲部分和离心力综合作用引起的二次流能提高传热系数[11-12]。Fan等[13]研究了有次流道的斜翅片细通道换热器内流体的传热特性,发现次流道能显著提高细通道换热器的传热能力。【本研究切入点】将弯曲结构和次流道同时应用到细通道热沉中的研究鲜有报道。【拟解决的关键问题】将弯曲结构应用到细通道热沉并基于锯齿状细通道热沉优化提出一种波状细通道热沉,还将次流道应用于波状细通道热沉中; 对有无次流道的波状细通道和常规直细通道热沉进行数值模拟,并应用熵产理论进行对比分析。
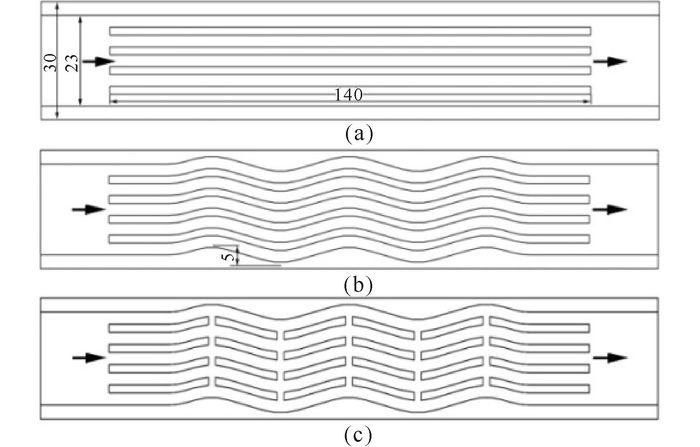
1 模型描述 1.1 几何模型3种细通道热沉的材料均选用铜,其三维模型采用一般CAD软件建立。图 1是3种细通道热沉的尺寸结构图。其中a是常规直细通道热沉CMS(conventional mini-channel heat sink),b是波状细通道热沉WMS(wave mini-channel heat sink),c是带次流道的波状细通道热沉WMS-S(wave mini-channel heat sink with secondary passages)。3种热沉细通道的截面均为3 mm×3 mm。在WMS的间壁上开截面尺寸为1 mm×1 mm的次流道制成WMS-S。
|
图 1 3种热沉结构 Fig.1 Structure of 3 different heat sinks |
对数值运算时的流体作如下假设:流体是稳态不可压缩层流流体;忽略流体的体积力、表面力、黏性耗散和辐射传热;流体的物性参数为常数。因此得到简化控制方程:
| $\begin{align} & \frac{\partial \left( \rho u\phi \right)}{\partial x}+\frac{\partial \left( \rho v\phi \right)}{\partial y}+\frac{\partial \left( \rho w\phi \right)}{\partial z}=\frac{\partial }{\partial x}\left( {{\mathit{\Gamma }}_{\phi }}~\frac{\partial \phi }{\partial x} \right)+ \\ & \frac{\partial }{\partial y}\left( {{\mathit{\Gamma }}_{\phi }}~\frac{\partial \phi }{\partial y} \right)+\frac{\partial }{\partial z}({{\mathit{\Gamma }}_{\phi }}~\frac{\partial \phi }{\partial z})+{{s}_{\phi }}, \\ \end{align}$ | (1) |
其中u、v、w分别表示x、y、z的速度分量;φ=1时,公式(1) 表示连续方程;φ=u、v和w时,公式(1) 表示动量方程;φ=T时,公式(1) 表示能量方程;Γφ表示通用耗散系数;Sφ在不同方程中表示不同源项。ρ为密度,kg/m3。
热沉的进口为速度边界条件,速度v=0.05~0.6 m/s,入口温度恒为300 K;热沉的出口设为压力边界条件,出口相对压力设为0;热沉底面设为恒热流边界条件,热流密度为5×104 W/m2;其他壁面均为绝热面。
采用商用CFD软件对上述方程进行求解,收敛系数取为1×10-6。
1.3 数学模型计算矩形截面流道的水力直径Dh的公式如下:
| ${{D}_{h}}=2wh/\left( w+h \right),$ | (2) |
式中w表示截面宽,m;h表示截面高,m。定义Re数(Reynolds number)如下:
| $Re=\frac{{{\rho }_{\text{f}}}{{D}_{\text{h}}}{{v}_{\text{m}}}}{{{\mu }_{\text{f}}}},$ | (3) |
vm为流体的平均速度,m/s;μ为动力粘度,Pa·s。下标f表示流体。
表面摩擦系数f计算公式如下:
| $f=\frac{2{{D}_{\text{h}}}\Delta p}{{{\rho }_{\text{f}}}v_{\text{m}}^{2}{{L}_{\text{c}}}},$ | (4) |
式中△p为进出口压降,Pa;Lc表示通道长,m。
定义传热系数k如下:
| $k=\frac{Q}{{{A}_{\text{w}}}w\Delta {{T}_{\text{m}}}},$ | (5) |
式中Q为加热壁面总热流,W;Aw为加热壁面积,m2;ΔTm为加热壁面和流体的平均温差,K;k为传热系数,W/(m2·K);
根据热力学第二定律建立通道内部流动与传热过程的熵产模型,其表达式如下:
| ${{E}_{h}}=\frac{k}{{{T}^{2}}}~\left( {{\left( \frac{\partial T}{\partial x} \right)}^{2}}+{{\left( \frac{\partial T}{\partial y} \right)}^{2}}+{{\left( \frac{\partial T}{\partial z} \right)}^{2}} \right),$ | (6) |
| $\begin{align} & {{E}_{f}}=\frac{\mu }{T}\left\{ 2\left[ {{\left( \frac{\partial u}{\partial x} \right)}^{2}}+{{\left( \frac{\partial v}{\partial y} \right)}^{2}}+{{\left( \frac{\partial w}{\partial z} \right)}^{2}} \right] \right.+\left( \frac{\partial u}{\partial y} \right.+ \\ & {{\left. \frac{\partial v}{\partial x} \right)}^{2}}+\left( \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x} \right)\left. ^{2}+{{\left( \frac{\partial v}{\partial z}\text{ }+\frac{\partial w}{\partial y}\text{ } \right)}^{2}} \right\}, \\ \end{align}$ | (7) |
式中T是流体温度,K。由式(7) 可知,体积熵产率由两部分不可逆性因素组成:流体流动引起的摩擦损失Ef及传热不可逆引起的损失Eh。
为了进一步分析比较,定义无量纲熵产率Eh*和Ef*[12],公式如下:
| $E_{h}^{*}=\frac{{{\int }_{V}}{{E}_{\text{h}}}\text{d}V}{m\prime {{c}_{p}}},$ | (8) |
| $E_{\text{f}}^{*}=\frac{{{\int }_{V}}{{E}_{\text{f}}}\text{d}V}{m\prime {{c}_{\text{p}}}},$ | (9) |
式中m′是流体的质量流量,kg/s;cp是流体的比热容,J/(kg·K);V为流体域体积,m3。
2 网格及数值方法检验 2.1 网格独立性检验为保证计算精度和缩短计算时间,对CMS的网格独立性进行验证。对进口流速为0.2 m/s的网格数级别分别按粗糙级别(120万)、精细级别(270万)和最精细级别(430万)的CMS进行数值模拟计算。将粗糙和精细级别网格数的CMS的进出口压降与最精细级别网格数进行对比,得到误差为6.7%和1.3%。可见精细级别的网格已满足要求,因此热沉计算模型的网格数均选用精细级别。
2.2 数值方法有效性检验采用文献[14]中的摩擦系数公式进行数值方法有效性验证,公式如下:
| $f={{f}_{\text{FD}}}+\frac{K{{D}_{\text{h}}}}{{{L}_{\text{c}}}},$ | (10) |
| $\begin{align} & {{f}_{\text{FD}}}Re=96(1-1.3553a+1.9467{{a}^{2}}- \\ & 1.7012{{a}^{3}}+0.9564{{a}^{4}}-0.2537{{a}^{5}}), \\ \end{align}$ | (11) |
| $\begin{align} & K=0.6797+1.2197a+3.3089{{a}^{2}}-9.5921{{a}^{3}}+ \\ & 8.9089{{a}^{4}}-2.9959{{a}^{5}})。\\ \end{align}$ | (12) |
式(8), 式(9) 中,a=w/h表示细通道截面宽高比。
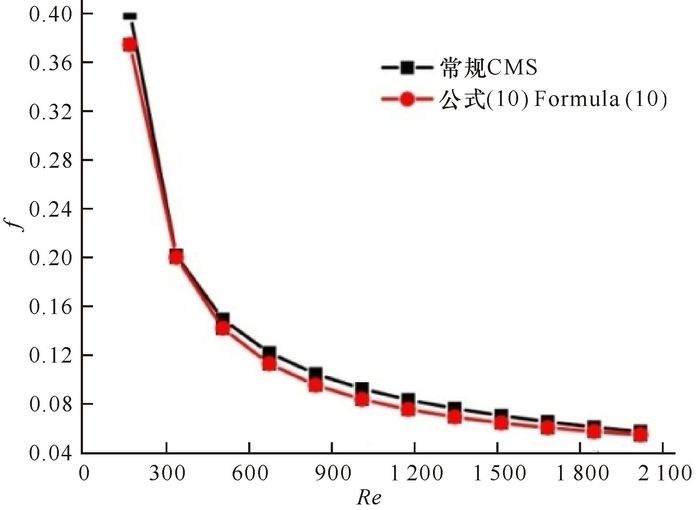
选用CMS进行数值方法有效性验证。数值模拟由公式(10) 计算出的摩擦系数, 对比见图 2。由图 2可看出数值模拟计算出的表面摩擦系数与公式(10) 的计算结果吻合度较高,因此CMS采用的数值方法是有效的。3种细通道热沉都采用同样的数值模拟方法。
|
图 2 CMS的摩擦系数验证 Fig.2 Verification of friction factor for CMS |
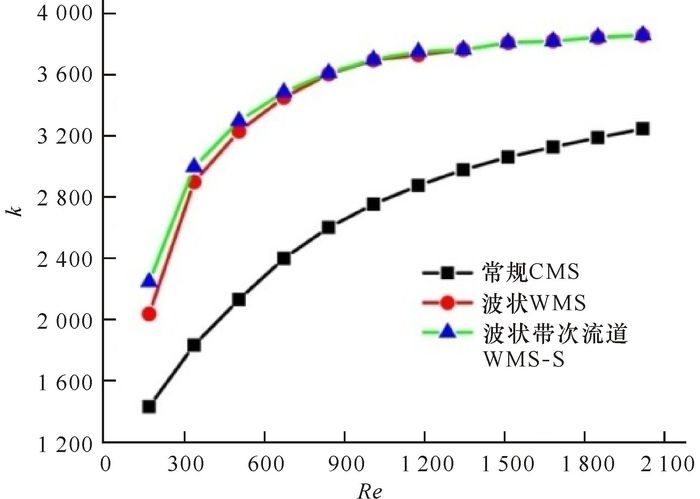
由图 3可看出,随着流体进口Re数的增加,3种细通道热沉的传热系数k均增加。WMS和WMS-S的传热系数k远高于CMS,因此可认为两种非直细通道热沉的传热能力较常规细通道热沉显著提升。对比WMS和WMS-S,发现在低Re数时,WMS-S的传热系数k大于WMS,因此认为在较低流速时,次流道可增强波状细通道热沉的换热能力。流体在波状细通道中的流动,经历二次流的产生减弱消失和再产生这种周而复始的循环过程,流体在这种循环过程中会导致其紊度变化而有助于传热强化。流进细通道弯曲部分的流体在形成二次流时,被次流道破坏,流体的流型被打乱,紊度增加导致传热强化。
|
图 3 3种热沉的k随进口流体Re数的变化 Fig.3 Relationship between k of 3 different heat sinks and Re number |
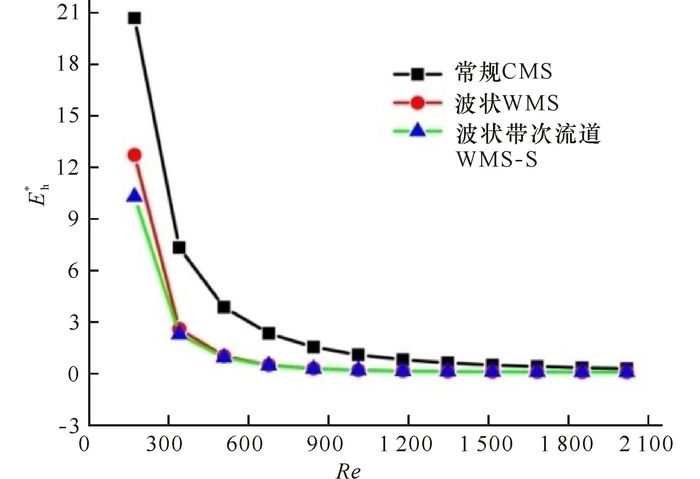
由图 4看出,3种细通道热沉的传热熵产率均随着进口流体流速的增加而逐渐减小,并趋于平缓。CMS的Eh*明显高于其他两种,说明CMS的有效能损失较大。WMS和WMS-S的Eh*相差不大,在进口流体Re数低于600时,WMS的略高于WMS-S,因此可认为在低流速状态下,次流道可以进一步减小波状细通道的能量损失。
|
图 4 传热熵产率随Re的变化 Fig.4 Variation of Eh* with Re number |
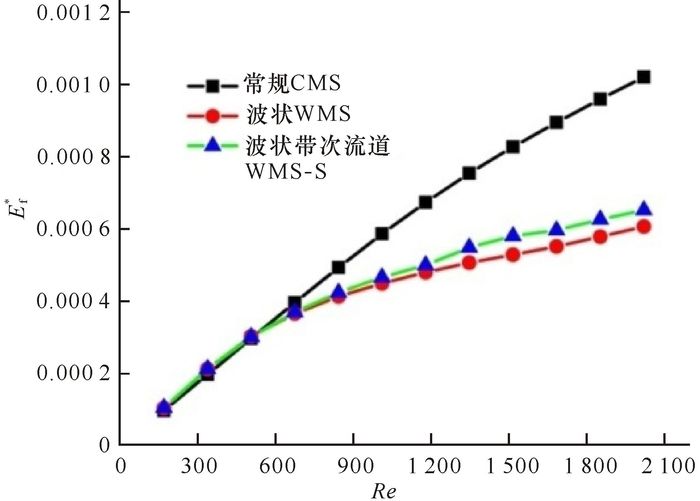
由图 5可看出,随着进口流体Re数的增加,3种细通道热沉的流动熵产率Ef*均增加,但在Re大于600时,WMS和WMS-S流动熵产率较CMS大幅减小。对比WMS和WMS-S,可发现,在Re大于600时,WMS的流动熵产率Ef*比WMS-S小。
|
图 5 流动熵产率随Re的变化 Fig.5 Variation of Eh* with Re number |
对比图 4和图 5发现,流动熵产率Ef*比传热熵产率Eh*小很多,因此可认为细通道热沉的能量损失主要取决于传热不可逆。
4 结论本研究通过对比分析CMS、WMS和WMS-S 3种不同结构形状的细通道热沉传热特性,得到以下结论:WMS和WMS-S的传热系数k比CMS显著增加,低Re数时,WMS-S比WMS的传热性能略有增加,且WMS-S的传热不可逆损失较小。
| [1] |
TUCKERMAN D B, PEASE R F W. High-performance heat sinking for VLSI[J]. IEEE Electron Device Letters, 1981, 2(5): 126-129. DOI:10.1109/EDL.1981.25367 |
| [2] |
WU H Y, CHENG P. Friction factors in smooth trapezoidal silicon microchannels with different aspect ratios[J]. International Journal of Heat and Mass Transfer, 2003, 46(14): 2519-2525. DOI:10.1016/S0017-9310(03)00106-6 |
| [3] |
WU H Y, CHENG P. An experimental study of convective heat transfer in silicon microchannels with different surface conditions[J]. International Journal of Heat and Mass Transfer, 2003, 46(14): 2547-2556. DOI:10.1016/S0017-9310(03)00035-8 |
| [4] |
夏国栋, 柴磊, 齐景智. 梯形硅基微通道热沉流体流动与传热特性研究[J]. 北京工业大学学报, 2011, 37(7): 1079-1084. XIA G D, CHAI L, QI J Z. Flow and heat transfer characteristics for water in a trapezoidal silicon microchannel heat sink[J]. Journal of Beijing University of Technology, 2011, 37(7): 1079-1084. |
| [5] |
唐慧敏, 吴慧英, 吴信宇. 锯齿形硅基微通道内流动与换热特性实验[J]. 航空动力学报, 2010, 25(6): 1264-1270. TANG H M, WU H Y, WU X Y. Experimental study of flow and heat transfer characteristics in silicon-based corrugated microchannels[J]. Journal of Aerospace Power, 2010, 25(6): 1264-1270. |
| [6] |
BEJAN A. Entrophy generation through heat and fluid flow[M]. New York: Wiley, 1982: 89-190.
|
| [7] |
BEJAN A. Entropy generation minimization[M]. Boca Raton: CRC Press, 1996: 77-111.
|
| [8] |
翟玉玲, 夏国栋, 刘献飞, 等. 复杂结构微通道热沉液体强化传热过程的热力学分析[J]. 化工学报, 2014, 65(9): 3403-3409. ZHAI Y L, XIA G D, LIU X F, et al. Thermodynamic analysis of enhanced heat transfer process in microchannel heat sinks with complex structure[J]. CIESC Journal, 2014, 65(9): 3403-3409. |
| [9] |
GUO J F, XU M T, TAO Y J, et al. The effect of temperature-dependent viscosity on entropy generation in curved square microchannel[J]. Chemical Engineering and Processing Process Intensification, 2012, 52: 85-91. DOI:10.1016/j.cep.2011.11.008 |
| [10] |
WANG Y S, ZHOU B, LIU Z C, et al. Numerical study and performance analyses of the mini-channel with discrete double-inclined ribs[J]. International Journal of Heat and Mass Transfer, 2014, 78: 498-505. DOI:10.1016/j.ijheatmasstransfer.2014.06.067 |
| [11] |
AKHAVAN-BEHABADI M A, PAKDAMAN M P, GHAZVINI M. Experimental investigation on the convective heat transfer of nanofluid flow inside vertical helically coiled tubes under uniform wall temperature condition[J]. International Communications in Heat and Mass Transfer, 2012, 39(4): 556-564. DOI:10.1016/j.icheatmasstransfer.2012.02.008 |
| [12] |
冯振飞, 何荣伟, 朱礼, 等. 周向平行细通道夹套的换热特性[J]. 过程工程学报, 2015, 15(6): 901-908. FENG Z F, HE R W, ZHU L, et al. Heat transfer characteristics of a jacket with circumferential parallel minichannels[J]. The Chinese Journal of Process Engineering, 2015, 15(6): 901-908. DOI:10.12034/j.issn.1009-606X.215266 |
| [13] |
FAN Y, LEE P S, JIN L W, et al. Experimental investigation on heat transfer and pressure drop of a novel cylindrical oblique fin heat sink[J]. International Journal of Thermal Sciences, 2014, 76: 1-10. DOI:10.1016/j.ijthermalsci.2013.08.007 |
| [14] |
XIA G D, CHAI L, WANG H Y, et al. Optimum thermal design of microchannel heat sink with triangular reentrant cavities[J]. Applied Thermal Engineering, 2011, 31(6/7): 1208-1219. |
 2017, Vol. 24
2017, Vol. 24 

