2. 钦州学院海洋学院,广西 钦州 535000
2. Ocean College, Qinzhou University, Qinzhou, Guangxi, 535000, China
【研究意义】水动力是反应海域水环境的一个重要指标,直接关系到海域水交换能力、污染物扩散、自净能力等方面,在海洋环境基础研究上具有重要地位。岸线变化是引起海域水动力变化的一个重要因素。近年来,岸线开发利用的加快显著地改变原有岸线的特征,同时也不同程度地影响海域水动力环境。开展岸线变化对海域水动力环境影响的研究,对合理开发利用岸线,保护海洋生态环境,保障海洋资源可持续发展等具有重要的科学和实践意义。钦州湾位于广西沿岸中部,地理位置为108°28′20″~108°45′30″E,21°33′20″~21°54′30″N。它拥有丰富的海洋资源,是我国西南出海的重要通道,区域经济发展地位突出,因此海洋环境保护对钦州湾可持续发展意义重大。【前人研究进展】目前,国内外学者已有大量的文献报道各研究海域的水动力变化。陈金瑞等[1]针对胶州湾内湾不同年代的5套岸线进行潮汐潮流的数值模拟研究,计算分析纳潮量、潮汐、潮流以及水交换等水动力因素的变化。鲁友鹏等[2]基于FVCOM对杭州湾南岸海域水动力特征进行模拟,在此基础上分析岸线变化造成的水动力影响累积效应。李小维等[3]采用二维潮流数学模型对铁山港湾海域的潮流场进行数值模拟,分析工程前后水动力变化情况。方神光等[4]利用遥感资料准确计算了过去近30年内伶仃洋水域面积和水域纳潮的演变情况。蒋磊明等[5]结合数值模拟及海流观测资料,对钦州湾海域纳潮量及水体半更换周期进行计算。张坤等[6]采用MIKE21 HD水动力模型对钦州湾水动力进行模拟,并计算钦州湾和茅尾海的纳潮量。孙永根等[7]利用数值模拟对钦州保税港区填海造地工程前后潮流动力场变化进行分析计算,并从潮流场、冲淤环境和纳潮量三方面的变化来说明大规模填海过程对钦州湾海洋环境影响。董德信等[8]从大规模围填海工程方面考虑其对钦州湾水动力环境的影响。【本研究切入点】近年来,钦州湾沿海开发力度加大,岸线、地形变化给钦州湾水动力环境造成一定的影响。虽有部分的研究报道钦州湾水动力环境变化情况,但尚不多见,更是缺乏有关其变化机制的研究。【拟解决的关键问题】本研究结合2004年及2012年海图、卫星影像资料等资料,采用数值模拟的方法对钦州湾2004年-2012年间岸线变化造成潮流、纳潮量、水交换能力的变化进行计算,分析岸线变化对钦州湾水动力环境的影响,为钦州湾海岸线开发、海洋环境保护提供科学依据。
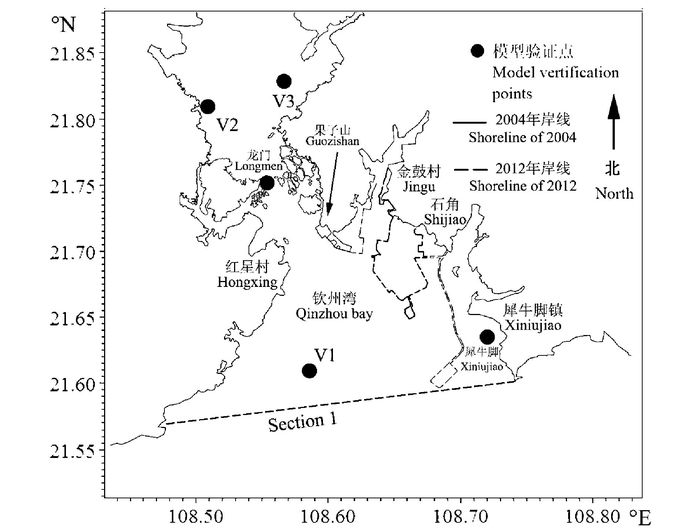
1 材料与方法 1.1 钦州湾岸线概述2004年-2012年,钦州湾岸线变化剧烈,极大地改变了原有的岸线形态,较为明显的区域为果子山至石角一带。果子山至金鼓江处港口建设占用岸线,同时存在部分填海,岸线向金鼓江左侧推进较为明显。金鼓江右侧的金鼓村至石角附近海域填海造陆程度较大,使得岸线大幅度向钦州湾方向推进。金鼓江左、右两侧岸线变化后,金鼓江口向外延伸,同时江口变得狭窄。石角处的三墩公路建成后,形成非透水结构向钦州湾延伸,使得海域分割现象明显(图 1)。
|
图 1 2004年-2012年间钦州湾岸线变化情况 Fig.1 Change of shareline of Qinzhou Bay during 2004 and 2012 |
采用丹麦水利研究所开发的MIKE 21 HD水动力模型建立钦州湾潮流数值模型。MIKE 21 HD水动力模型具有良好的便捷性、准确性、高效性等特点,使其在水动力模拟上得到广泛地应用,其模型包括一个连续方程及两个动量方程[9]。
连续方程:
| $\frac{\partial \zeta }{\partial t}+\frac{\partial p}{\partial x}+\frac{\partial q}{\partial y}=\frac{\partial h}{\partial t},$ | (1) |
X方向动量方程:
| $\begin{align} & \frac{\partial p}{\partial t}+\frac{\partial }{\partial x}(\frac{{{p}^{2}}}{H})+\frac{\partial }{\partial y}\left( \text{ }\frac{pq}{H} \right)+gH\frac{\partial \zeta }{\partial x}+ \\ & \frac{gp\sqrt{{{p}^{2}}+{{q}^{2}}}~}{{{C}^{2}}{{H}^{2}}~}-\frac{1}{{{\rho }_{w}}}~\left[ \frac{\partial }{\partial x}\left( H{{\tau }_{xx}} \right)+\frac{\partial }{\partial y}\left( H{{\tau }_{xy}} \right) \right]- \\ & \mathsf{\Omega }q-fV{{V}_{x}}=0, \\ \end{align}$ | (2) |
Y方向动量方程:
| $\begin{align} & \frac{\partial q}{\partial t}+\frac{\partial }{\partial y}(\frac{{{q}^{2}}}{H})+\frac{\partial }{\partial x}\left( \frac{pq}{H} \right)+gH\frac{\partial \zeta }{\partial y}+ \\ & \frac{gq\sqrt{{{p}^{2}}+{{q}^{2}}}~}{{{C}^{2}}{{H}^{2}}}-\frac{1}{{{\rho }_{w}}}~\left[ \frac{\partial }{\partial y}\left( H{{\tau }_{yy}} \right)+\frac{\partial }{\partial x}\left( H{{\tau }_{xy}} \right) \right]- \\ & \mathsf{\Omega }q-fV{{V}_{y}}=0, \\ \end{align}$ | (3) |
式中:ζ为水位;h为水深;H=h+ζ;p、q分别为x、y方向的单宽流量;C为谢才系数,与曼宁系数的关系为C=n-1/h1/6;g为重力加速度,f为风摩擦系数;V、Vx、Vy分别为风速及其在x、y方向的分量;Ω为科氏力系数;ρw为水的密度;x、y为距离;t为时间;u、v分别为潮流在x、y方向的速度分量;τxx、τxy、τyy分别为各方向剪切应力。
1.2.2 纳潮量的计算本研究采用数值模拟的方法对纳潮量进行计算,其计算过程如下:对区域进行网格化;利用数值模拟结果,计算每个网格水体体积的变化,得出每个网格纳潮量;将所有网格的纳潮量相加,得出整个区域的纳潮量。假设将某个区域划分为N个网格,第i个网格的面积为Si,对应的平均高、低潮潮位高分别为h1、h2,则第i个网格的纳潮量Wi为
| ${{W}_{i}}={{S}_{i}}\times \left( {{h}_{1}}-{{h}_{2}} \right),$ | (4) |
整个区域的纳潮量W为
| $W=\sum\limits_{i=1}^{N}{{{W}_{i}}}\left( i=1,\cdots ,\text{ }N \right)。$ | (5) |
水交换能力的常见表达方式是水体半交换时间,水体半交换时间为某海域保守物质浓度通过对流扩散稀释后,其浓度达到初始浓度一半所需的时间[10]。海域水体半交换时间的计算需要建立污染物输移扩散模型,以保守物质作为计算因子,并赋予模型一个初始浓度值,当计算域内物质的量达到初始时刻的50%时,所模拟的时长即为海域水体半交换时间。
本研究采用MIKE 21 TS污染物输运模型建立钦州湾污染物输移扩散模型,对海域水交换能力进行计算,其控制方程为
| $\begin{align} & \frac{\partial }{\partial t}\left( hc \right)+\frac{\partial }{\partial x}\left( uhc \right)+\frac{\partial }{\partial y}\left( vhc \right)=\frac{\partial }{\partial x}(h\cdot {{D}_{x}}\cdot \\ & \partial c\text{ }\partial x\text{ })+\frac{\partial }{\partial y}\left( h\cdot {{D}_{y}}\cdot \frac{\partial c}{\partial y} \right)-k\cdot c\cdot h+S, \\ \end{align}$ | (6) |
式中:c为污染物的浓度;u、v分别为潮流在x、y方向的速度分量;h为水深;Dx、Dy分别为污染物在x、y方向的扩散系数;k为线性衰减系数,采用保守物质作为计算因子时,其取值为0;S为源漏项,其取值根据污染源的实际排放量确定。
1.3 计算区域的确定及网格划分根据2004年及2012年钦州湾岸线地形资料,对不同岸线条件下的海域进行网格划分。计算区域西边界取至企沙镇,东边界取至中三墩,南边界取至钦州湾外湾,北边界取至整个茅尾海,东西方向长约38 km,南北方向长约47 km。采用适应性较好的不规则结构网格对区域进行划分,并就复杂的岛屿和岸线进行局部加密,以保证计算精度,最小边长为50 m,最大水深约21 m。2004年岸线计算网格共包涵13 497个节点、25 770个单元,2012年岸线计算网格共包涵17 478个节点、33 109个单元。
1.4 模型验证为验证水动力模型的可靠性,采用2012年5月(小潮)及2012年6月(大潮)实测水文资料对计算结果进行验证,包括两个潮位验证点及三个潮流验证点,各潮流要素验证点点位如图 1所示,其中犀牛脚、龙门为潮位验证点,V1~V3为流速流向验证点。由于篇幅有限,这里只列举部分点位的结果验证。
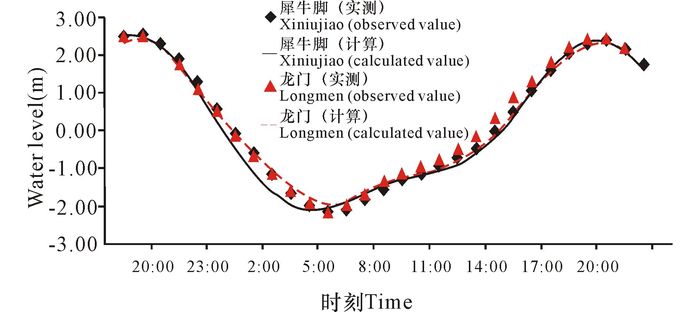
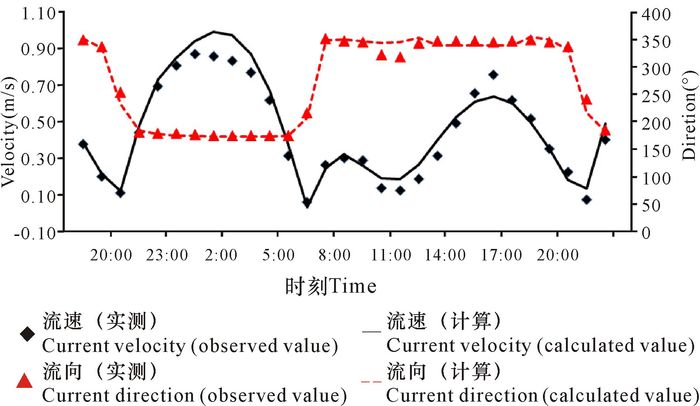
由图 2、图 3可知,龙门及犀牛脚两站的潮位计算值与实测值相差不大,两站的潮位过程与实际监测结果几乎一致。V1站流速计算值在高潮位变化过程与实测值稍有偏差,个别时段流速计算值比实测值略小,但流速和流向的变化过程与实测值基本吻合。总体上来说,模型计算值与实测值吻合良好,各位相、量值及过程线与实际情况基本一致,说明模型计算结果可以反映海域实际的水动力过程。
|
图 2 潮位验证图(大潮) Fig.2 Verification of tidal level in Spring tide |
|
图 3 V1站流速、流向验证图(大潮) Fig.3 Verification of current velocity and current direction in V1(Spring tide) |
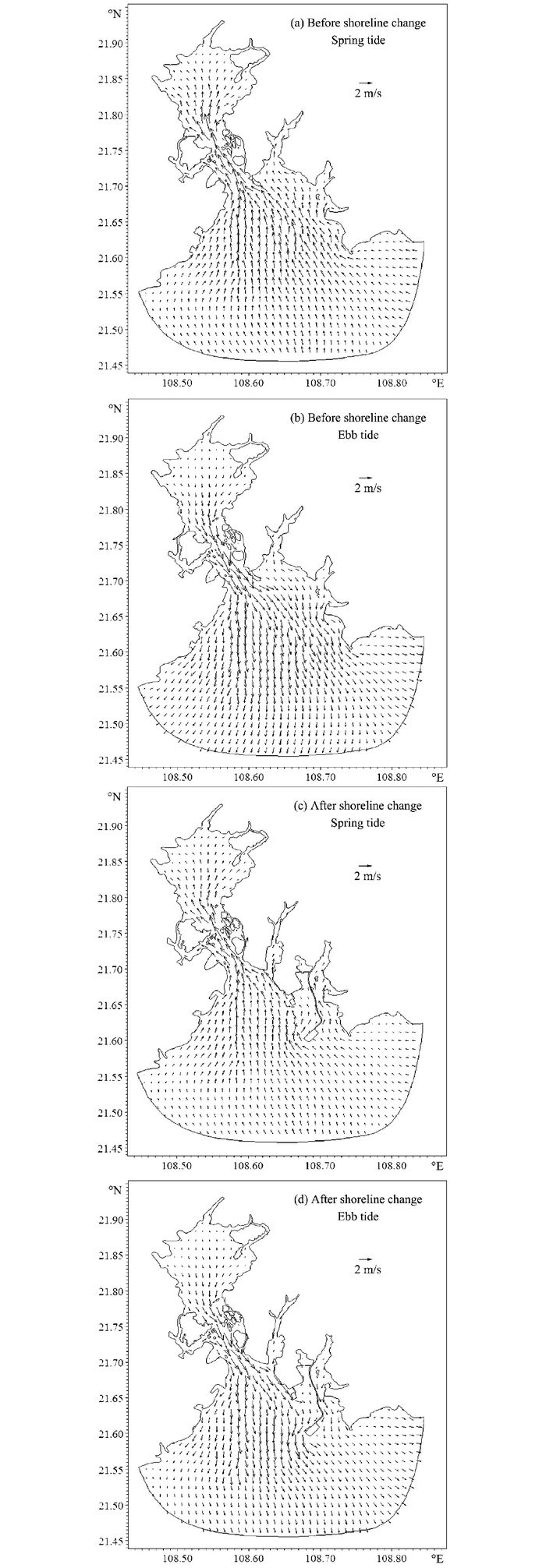
由图 4中可知,果子山至石角之间的近岸海域的水动力变化明显。岸线变化前,果子山至石角一带附近海域潮流基本上呈天然状态,流速、流向分布较为均匀。岸线变化后,海域水动力变化明显,岸线向海延伸,占用海域,使得果子山至石角附近部分海域不复存在。三墩公路建成后,潮流在三墩公路顶端形成局部绕流现象,造成局部流速增大,最高增幅约为0.2 m/s;同时由于其对海域形成分割作用,使得犀牛脚镇附近海域流速降低,水动力减弱,相比于岸线变化前,其流速下降超过0.1 m/s。部分海域流向也发生明显变化:岸线变化前,三墩公路附近海域涨潮时流向基本呈东南方向;而岸线变化后,其西侧流向变为西南向,东侧流向变为近北向,落潮时流向也有一定的变化。可见,岸线变化对钦州湾海域局部水动力环境造成一定的影响,尤其是果子山至石角一带附近海域。
|
图 4 岸线变化前后海域涨落急流场分布 Fig.4 Current field of Spring and Ebb tide before and after shoreline change tide |
以图 1中断面1为基准,对断面1以北的海域纳潮量进行计算。如表 1所示,岸线变化对海域纳潮量有显著影响:岸线变化前,海域大、小潮纳潮量分别约为1.45×109 m3和2.66×108 m3;岸线变化后,海域大、小潮纳潮量分别为1.30×109 m3和2.37×108 m3。相比于岸线变化前,岸线变化后大、小潮期间海域纳潮量均有所降低,变化幅度分别为-1.50×108 m3和-0.29×108 m3,下降比例分别为纳潮总量的10.3%和10.9%。
| 表 1 岸线变化前后海域纳潮量 Table 1 Tidal prism of sea area before and after shoreline change |
岸线变化一方面占用部分海域水体,使得海域接纳外海传入水体的体积减少;另一方面改变海域岸线变化区域附近的水动力,造成局部区域水动力减弱,从而减小了海域的纳潮量。岸线变化后,果子山至石角一带岸线向海延伸占用大片海域,其结果使得本应进入这部分海域的潮水不复存在;与此同时,三墩公路的分割作用还降低了三墩公路附近的潮流流速,削减外来水体进入湾内的能力。因此,岸线变化后钦州湾海域纳潮量减小幅度较大。
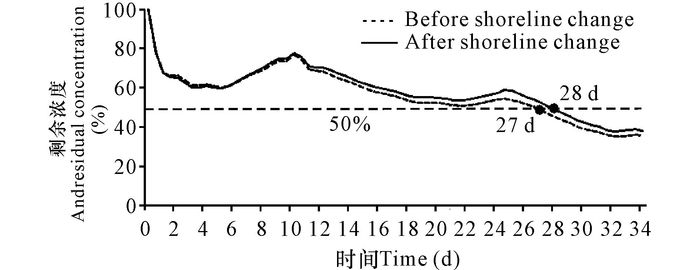
2.3 水交换能力对图 1断面1以北的海域水交换能力进行计算。由图 5可知,模拟开始时段,不同岸线对水交换程度的影响区别不是很大,前10 d左右变化幅度基本相同,10 d后水交换程度的差异逐渐表现出来,且差异随时间的推移越来越大。海域保守物质达到初始时刻的50%时,岸线变化前需约27 d,而岸线变化后则需要28 d,即海域水体半交换时间在岸线变化前为27 d,岸线变化后为28 d。相比于岸线变化前,岸线变化后海域水体半交换时间延长1 d,表明岸线变化对海域水交换能力有一定的影响。
|
图 5 岸线变化前后水体交换变化特征 Fig.5 The hydrodynamic features of water exchange between after and before shoreline change |
水交换能力的变化主要由水动力特征的变化而引起。岸线变化前,海域潮流速度较大,潮流呈天然的流态,基本不受干扰。岸线变化后,部分海域水动力变弱,潮流流速降低,使得海域水交换能力变弱。三墩公路建成后,附近海域流场形态改变、流速变小,潮流过流断面减小,海域水动力、水交换能力下降,因此海域水体半交换时间增加。
3 结论岸线变化对钦州湾水动力环境有一定的影响,尤其是果子山至石角附近海域。岸线变化后,潮流在三墩公路顶端形成绕流现象,造成局部流速增大,最大增幅约为0.2 m/s;而在犀牛脚附近海域,流速则下降约0.1 m/s。岸线变化改变钦州湾原有的流态,三墩公路附近涨潮时流向由岸线变化前的东南方向变为西南向或正北向。
岸线变化对海域纳潮量有较为明显的影响。岸线变化后,海域大、小潮期间海域纳潮量分别下降约-1.50×108 m3和-0.29×108 m3,下降幅度分别约为纳潮总量的10.3%和10.9%,这与岸线向海延伸占用海域以及形成的局部海域分割导致水动力减弱有关。
岸线变化使得海域水半交换时间延长。岸线变化前,海域水体半交换时间为27 d;岸线变化后,海域水体半交换时间为28 d,海域水体交换时间延长1 d。岸线变化后,海域整体水动力变弱,削弱海域的水交换能力,从而造成水体半交换时间的延长。
| [1] |
陈金瑞, 陈学恩. 近70年胶州湾水动力变化的数值模拟研究[J]. 海洋学报, 2012, 34(4): 30-41. CHEN J R, CHEN X E. Numerical simulation of the hydrodynamic evolution of the Jiaozhou Bay in the last 70 years[J]. Acta Oceanologica Sinica, 2012, 34(4): 30-41. |
| [2] |
鲁友鹏, 梁书秀, 孙昭晨, 等. 杭州湾南岸岸线变化对水动力的影响累积效应[J]. 海洋环境科学, 2015, 34(3): 384-390. LU Y P, LIANG S X, SUN Z C, et al. Cumulative effects of topography change on waterway's hydrodynamic along the southern coast of Hangzhou Bay[J]. Marine Environmental Science, 2015, 34(3): 384-390. |
| [3] |
李小维, 裴木凤. 铁山港湾港口总体规划用海对海水动力环境的影响预测[J]. 广西科学, 2015, 22(3): 274-280. LI X W, PEI M F. Impact prediction of sea engineering of Tieshangang Bay port overall planning on hydrodynamic environment[J]. Guangxi Sciences, 2015, 22(3): 274-280. |
| [4] |
方神光, 陈文龙, 崔丽琴. 伶仃洋水域纳潮量计算及演变分析[J]. 海洋环境科学, 2012, 31(1): 76-78. FANG S G, CHEN W L, CUI L Q. Analysis on evolvement of tidal prism of Lingdingyang Bay[J]. Marine Environmental Science, 2012, 31(1): 76-78. |
| [5] |
蒋磊明, 陈波, 邱绍芳, 等. 钦州湾潮流模拟及其纳潮量和水交换周期计算[J]. 广西科学, 2009, 16(2): 193-195, 199. JIANG L M, CHEN B, QIU S F, et al. Calculation of tidal prism and water exchange period and simulation of current about Qinzhou Bay[J]. Guangxi Sciences, 2009, 16(2): 193-195, 199. |
| [6] |
张坤, 娄安刚, 孟云, 等. 钦州湾海域纳潮量和水交换能力的数值模拟研究[J]. 海洋环境科学, 2014, 33(4): 585-591. ZHANG K, LOU A G, MENG Y, et al. Numerical study on the tidal prism and water exchange ability of Qinzhou Bay[J]. Marine Environmental Science, 2014, 33(4): 585-591. |
| [7] |
孙永根, 高俊国, 朱晓明. 钦州保税港区填海造地工程对海洋环境的影响[J]. 海洋科学, 2012, 36(12): 84-89. SUN Y G, GAO J G, ZHU X M. Effect of reclamation engineering in Qinzhou Bond Harbor on marine environment of Qinzhou Bay[J]. Marine Sciences, 2012, 36(12): 84-89. |
| [8] |
董德信, 李谊纯, 陈宪云, 等. 大规模填海工程对钦州湾水动力环境的影响[J]. 广西科学, 2014, 21(4): 357-364, 369. DONG D X, LI Y C, CHEN X Y, et al. Impacts of hydrodynamic environment caused by large-scale reclamation in Qinzhou Bay[J]. Guangxi Sciences, 2014, 21(4): 357-364, 369. |
| [9] |
许婷. 丹麦MIKE 21模型概述及应用实例[J]. 水利科技与经济, 2010, 16(8): 867-869. XU T. Calculation principle and application example of a two-dimensional flow Model-MIKE21 HD[J]. Water Conservancy Science and Technology and Economy, 2010, 16(8): 867-869. |
| [10] |
魏皓, 田恬, 周锋, 等. 渤海水交换的数值研究-水质模型对半交换时间的模拟[J]. 青岛海洋大学学报, 2002, 32(4): 519-525. WEI H, TIAN T, ZHOU F, et al. Numerical study on the water exchange of the Bohai Sea: Simulation of the half-life time by dispersion model[J]. Journal of Ocean University of Qingdao, 2002, 32(4): 519-525. |
 2017, Vol. 24
2017, Vol. 24 

