【研究意义】近几年,轮式移动机器人的轨迹跟踪控制问题受到了广泛的关注和研究,它不仅具有非线性、强耦合和非完整约束,还具有外部扰动和参数不确定性。一些非线性控制策略被应用到该领域,包括自适应控制[1]、神经网络控制[2]、鲁棒控制[3]和滑模控制[4]等。Zeng等[2]利用自适应神经网络技术和高增益状态观测技术设计了一种新的自适应控制器,克服了系统中参数未知和不可测状态带来的困难。【前人研究进展】 Xin等[3]结合扰动观测器和自适应补偿器处理移动机器人动态系统的不确定性。沈艳军等[5]和陈武华等[6]介绍了非线性系统的自适应观测器,可用于观测移动机器人动力学模型中的扰动以提高系统的鲁棒性。Huang等[7]研究了轮式移动机器人输入受限问题。轮式移动机器人作为具有饱和执行器的不确定系统,可用黎艳等[8]的控制方法来处理。另外,很多文献将滑模控制应用于轮式移动机器人的研究中。Park等[9]针对轮式移动机器人的运动学、动力学和电机动力学模型,利用反步法和动态面技术设计了具有σ修正的电压自适应控制器,实现了轨迹跟踪控制。针对模型中存在未知参数或外部扰动的情形,Hou等[10]和Hwang等[11]设计了自适应鲁棒模糊控制器来解决轨迹跟踪控制问题。Do等[12]和Wang等[13]结合Lyapunov函数法和反步法设计了输出反馈控制器,使得机器人渐近跟踪上期望轨迹。Zhu等[14]和Buccieri等[15]分别利用横截函数方法和微分平坦方法设计了轨迹跟踪与镇定统一控制器。Ou等[16]和Mija等[17]针对轮式移动机器人动力学模型利用滑模变结构设计了有限时间轨迹跟踪控制器。Li等[18]将神经网络应用于非线性系统,而移动机器人系统亦可引入智能控制。例如,Boukens等[19]针对存在时变参数不确定性和外部干扰的移动机器人轨迹跟踪问题,结合最优控制、神经网络和鲁棒控制技术设计了智能控制器。【本研究切入点】受Lu等[20]的启发,本研究针对存在外界扰动和参数不确定性的轮式移动机器人设计了有限时间轨迹跟踪控制器。相对于先前的研究方法,本研究没有使用反步法,从而避免了反复使用虚拟控制器带来的积分膨胀问题。【拟解决的关键问题】为了便于轨迹跟踪控制器的设计,本研究将轮式移动机器人动态系统分为与线速度和角速度相关的两个子系统。首先,设计自适应快速终端滑模控制律,使得机器人的姿态角跟踪误差在有限时间内收敛到一个任意小的区域内,再设计线速度控制律,来保证位置跟踪误差的收敛性。
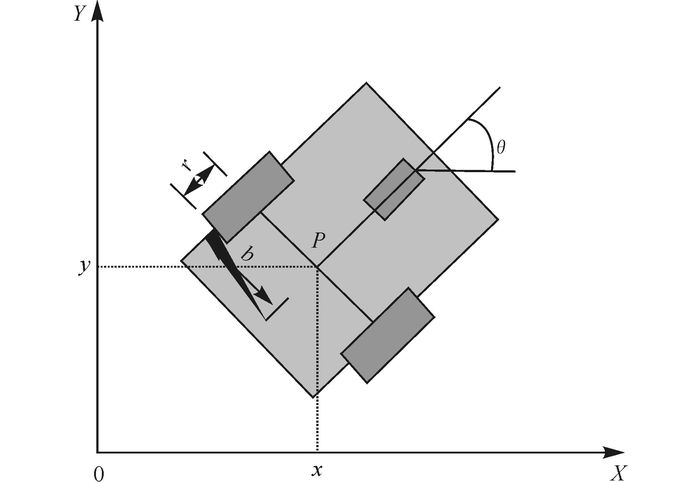
1 问题描述本研究讨论的机器人模型如图 1所示。移动机器人由后部两轮进行驱动,驱动轮半径为r,间距为2b,质心为P。定义移动机器人在世界坐标系X-O-Y的位姿状态为q=(x, y, θ)T,x和y分别为P点的横纵坐标,θ为移动机器人正方向与OX轴的夹角,其线速度为ν,角速度为ω。
|
图 1 轮式移动机器人模型 Fig.1 Wheeled mobile robot model |
轮式移动机器人的动态模型可以表示如下:
| $\dot{q}=S\left( q \right)\eta ,$ | (1) |
| $M\left( q \right)\ddot{q}+C\left( q,\dot{q} \right)+F\left( {\dot{q}} \right)+{{\tau }_{d}}=B\left( q \right)\tau -{{A}^{\text{T}}}\left( q \right)\lambda ,$ | (2) |
其中,η=(ν, ω)T为线速度和角速度组成的向量;τ=(τ1, τ2)T表示左右轮对应的转矩,M是一个对称的正定矩阵,C(q,
假设机器人的质心和几何中心重合在P点,那么C(q,
| $\begin{align} & S\left( q \right)=\left[ \begin{matrix} \text{cos}\ \theta & 0 \\ \text{sin}\ \theta & 0 \\ 0 & 1 \\ \end{matrix} \right],M\left( q \right)=\left[ \begin{matrix} m & 0 & 0 \\ 0 & m & 0 \\ 0 & 0 & J \\ \end{matrix} \right], \\ & B\left( q \right)=\frac{1}{r}\left[ \begin{matrix} \text{cos}\ \theta & \text{cos}\ \theta \\ \text{sin}\ \theta & \text{sin}\ \theta \\ b & -b \\ \end{matrix} \right],\text{ }A\left( q \right)={{\left[ \begin{matrix} -\text{sin}\ \theta \\ \text{cos}\ \theta \\ 0 \\ \end{matrix} \right]}^{\text{T}}}, \\ \end{align}$ |
其中,m是移动机器人质量,J代表其转动惯量。
在移动机器人满足非完整限制的情况下,A(q)
| $\ddot{q}=S\left( q \right)\dot{\eta }+\dot{S}\left( q \right)\eta ,$ | (3) |
将式(3) 代入式(2),得到:
| $\begin{align} & M\left( q \right)S\left( q \right)\dot{\eta }+M\left( q \right)\dot{S}\left( q \right)\eta +C\left( q,\dot{q} \right)+F\left( {\dot{q}} \right)+ \\ & {{\tau }_{d}}=B\left( q \right)\tau -{{A}^{\text{T}}}\left( q \right)\lambda 。\\ \end{align}$ | (4) |
根据M(q)、S(q)、A(q)和C(q,
ST(q)AT(q)=0,ST(q)M(q)
将式(4) 左乘ST(q),并化简可得:
| $\bar{M}\dot{\eta }+d=\bar{B}\tau ,$ | (5) |
其中,
进一步可以得到简化的机器人动力学模型:
| $\begin{align} & \left\{ \begin{array}{*{35}{l}} \dot{x}=v\text{cos}~\theta \\ \dot{y}=v\text{sin}~\theta \\ \dot{\theta }=\omega \\ \end{array} \right., \\ & \left\{ \begin{array}{*{35}{l}} m\dot{v}={{u}_{1}}+{{d}_{1}} \\ J\dot{\omega }={{u}_{2}}+{{d}_{2}} \\ \end{array} \right., \\ \end{align}$ | (6) |
其中,
设移动机器人参考轨迹为
| $\left\{ \begin{array}{*{35}{l}} \dot{x}{{~}_{r}}={{v}_{r}}\text{cos}\ {{\theta }_{r}} \\ {{{\dot{y}}}_{r}}={{v}_{r}}\text{sin}\ {{\theta }_{r}} \\ \dot{\theta }{{~}_{r}}={{\omega }_{r}} \\ \end{array} \right.。$ | (7) |
跟踪误差定义为
| $\left[ \begin{matrix} {{x}_{e}} \\ {{y}_{e}} \\ {{\theta }_{e}} \\ \end{matrix} \right]=~\left[ \begin{matrix} \text{cos}\ \theta & ~\text{sin}\ \theta & 0 \\ -\text{sin}\ \theta & \text{cos}\ \theta & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} x-{{x}_{r}} \\ y-{{y}_{r}} \\ \theta -{{\theta }_{r}} \\ \end{matrix} \right],$ | (8) |
进一步得到:
| $\left\{ \begin{array}{*{35}{l}} \dot{x}{{~}_{e}}=v-{{v}_{r}}\text{cos}\ {{\theta }_{e}}+\omega {{y}_{e}} \\ {{{\dot{y}}}_{e}}={{v}_{r}}\text{sin}\ {{\theta }_{e}}-\omega {{x}_{e}} \\ {{{\dot{\theta }}}_{e}}=\omega -{{\omega }_{r}}={{\omega }_{e}} \\ \end{array} \right.。$ | (9) |
下面将误差系统分为两个子系统,一个二阶子系统:
| $\left\{ \begin{array}{*{35}{l}} \dot{\theta }{{~}_{e}}={{\omega }_{e}} \\ J\dot{\omega }={{u}_{2}}+{{d}_{2}} \\ \end{array} \right.,$ | (10) |
和一个三阶子系统:
| $\left\{ \begin{array}{*{35}{l}} {{{\dot{x}}}_{e}}=v-{{v}_{r}}\text{cos}\ {{\theta }_{e}}+\omega {{y}_{e}} \\ {{{\dot{y}}}_{e}}={{v}_{r}}\text{sin}\ {{\theta }_{e}}-\omega {{x}_{e}} \\ m\dot{v}={{u}_{1}}+{{d}_{1}} \\ \end{array} \right.。$ | (11) |
为了便于叙述,给出如下引理和假设。
引理2.1[8] 对于非线性系统,如果存在李雅普诺夫函数V(x)和实数λ1>0,λ2>0以及0<κ<1使得
假设2.1 集总扰动d1和d2都是有界的,即d1 ≤dmax ,|d2|≤dmax,其中dmax为一个正常数。
2.1 角速度的有限时间控制器设计本节中,选取如下滑模面:
S1=ωe+k1θe+k2Sau1,
| ${{S}_{au1}}=\left\{ \begin{array}{*{35}{l}} \theta _{e}^{r},\quad if\quad \bar{S}{{~}_{1}}=0\ \ or\quad {{{\bar{S}}}_{1}}\ne 0,\text{ }\left| {{\theta }_{e}} \right|\ge \varepsilon \\ {{\iota }_{1}}{{\theta }_{e}}+{{\iota }_{2}}\text{sign}\left( {{\theta }_{e}} \right)\theta _{e}^{2},~\quad \text{if}\quad \bar{S}{{~}_{1}}\ne 0,\left| {{\theta }_{e}} \right|<\varepsilon \\ \end{array} \right.,$ |
其中,
| $J{{{\dot{S}}}_{1}}={{F}_{2}}+{{u}_{2}},$ | (12) |
其中,F2=-J
| $\begin{align} & {{E}_{v}}= \\ & \left\{ \begin{array}{*{35}{l}} r\ \theta _{e}^{r-1},~\quad \text{if}\quad {{{\bar{S}}}_{1}}=0\ \text{or}\quad \bar{S}{{~}_{1}}\ne 0,\left| {{\theta }_{e}} \right|\ge \varepsilon \\ {{\iota }_{1}}I+2{{\iota }_{2}}\text{sin}\left( {{\theta }_{e}} \right){{\theta }_{e}},~~\quad \text{if}\quad {{{\bar{S}}}_{1}}\ne 0,\left| {{\theta }_{e}} \right|<\varepsilon \\ \end{array} \right.。\\ \end{align}$ |
引理2.2 如果S1=S1=0,那么系统可在有限时间内达到ωe=0,θe=0。
证明 如果S1=S1=0,那么ωe=-k1θe-k2θer。选取李雅普诺夫函数Vθe=
| ${{{\dot{V}}}_{{{\theta }_{e}}}}+2{{k}_{1}}{{V}_{{{\theta }_{e}}}}+{{k}_{2}}{{2}^{~\frac{r+1}{2}~}}{{V}^{\frac{r+1}{\theta _{e}^{2}}}}~\le 0。$ |
由引理2.1可知,θe可以在有限时间T1内收敛到零,其中,
| ${{T}_{1}}\le {{T}_{0}}+\frac{1}{2{{k}_{1}}\left( \frac{1-r}{2} \right)}\text{ln}\ \frac{{{k}_{1}}{{V}^{\frac{1-r}{\theta _{e}^{2}}}}\left( {{\theta }_{e}}\left( 0 \right) \right)+{{k}_{2}}}{{{k}_{2}}}。$ |
假设2.2 在系统(12) 中,包含外部扰动和参数不确定性的集总扰动f2满足:|F2|≤J|
实际中,外部扰动是有界的,参考轨迹的θr和ωr也是有界的,因此假设2.2是合理的。于是,设计了如下自适应控制器:
| ${{u}_{21}}=-{{\alpha }_{1}}{{S}_{1}}-{{u}_{adp}},$ | (13) |
其中,α1S1是反馈部分,自适应估计律uadp用来压制集总扰动,其设计如下:
| ${{u}_{adp}}=\left\{ \begin{array}{*{35}{l}} \frac{{{S}_{1}}}{\left| {{S}_{1}} \right|}{{{\hat{\chi }}}_{1}},~\quad \text{if}\left| {{S}_{1}} \right|~{{{\hat{\chi }}}_{1}}>{{\varepsilon }_{1}} \\ \frac{{{S}_{1}}}{{{\varepsilon }_{1}}}~\hat{\chi }_{1}^{2},\quad \text{if}\left| {{S}_{1}} \right|~{{{\hat{\chi }}}_{1}}\le {{\varepsilon }_{1}} \\ \end{array} \right.,$ | (14) |
其中,ε1>0是待定设计参数,
| $\begin{align} & {{{\dot{\hat{\zeta }}}}_{1}}=-{{\varepsilon }_{1}}\hat{\zeta }{{~}_{1}}+\bar{p}{{~}_{1}}\left| {{S}_{1}} \right|, \\ & {{{\dot{\hat{\vartheta }}}}_{1}}=-{{\varepsilon }_{2}}{{{\hat{\vartheta }}}_{1}}+{{{\bar{q}}}_{1}}\left| {{S}_{1}} \right|\left| {{\xi }_{1}} \right|, \\ \end{align}$ | (15) |
其中,p1>0,q1>0以及ε1>0,ε2>0都是待定设计参数。令
定理2.1 根据动态系统(10),通过控制器(13) 以及自适应律(14),S1,
证明 证明过程分为两步。
步骤1:在|S1|
| ${{V}_{1}}=\frac{1}{2}\left( S_{1}^{\text{T}}J{{S}_{1}}+\frac{1}{{{{\bar{p}}}_{1}}}\tilde{\zeta }_{1}^{2}~+\frac{1}{{{{\bar{q}}}_{2}}}~\tilde{\vartheta }_{1}^{2} \right),$ |
对其求导可得:
| ${{{\dot{V}}}_{1}}=-\left( {{\alpha }_{1}}S_{1}^{2}+{{S}_{1}}{{u}_{adp}} \right)+{{F}_{2}}-\frac{1}{{\bar{p}}}{{~}_{1}}{{{\dot{\hat{\zeta }}}}_{1}}\tilde{\zeta }{{~}_{1}}-\frac{1}{{\bar{q}}}{{~}_{1}}{{{\dot{\hat{\vartheta }}}}_{1}}{{{\tilde{\vartheta }}}_{1}},$ | (16) |
由假设2.2可得:
| $\begin{align} & {{{\dot{V}}}_{1}}\le -\left( {{\alpha }_{1}}S_{1}^{2}+{{S}_{1}}{{u}_{adp}} \right)+{{\zeta }_{1}}\left| {{S}_{1}} \right|+ \\ & {{\vartheta }_{1}}\left| {{S}_{1}} \right|\left| {{\xi }_{1}} \right|-\frac{1}{{{{\bar{p}}}_{1}}}{{{\dot{\hat{\zeta }}}}_{1}}{{\xi }_{1}}-\frac{1}{{{{\bar{q}}}_{1}}}{{{\dot{\hat{\vartheta }}}}_{1}}{{{\tilde{\zeta }}}_{1}}, \\ \end{align}$ |
将自适应律代入可得:
| $\begin{align} & {{{\dot{V}}}_{1}}\le -\left( {{\alpha }_{1}}S_{1}^{2}+{{S}_{1}}{{u}_{adp}} \right)+{{\zeta }_{1}}\left| {{S}_{1}} \right|+ \\ & {{\vartheta }_{1}}\left| {{S}_{1}} \right|\left| {{\xi }_{1}} \right|-\frac{1}{{{{\bar{p}}}_{1}}}{{{\dot{\hat{\zeta }}}}_{1}}{{{\tilde{\zeta }}}_{1}}-\frac{1}{{{{\bar{q}}}_{1}}}{{{\dot{\hat{\vartheta }}}}_{1}}{{{\tilde{\vartheta }}}_{1}}\le -({{\alpha }_{1}}S_{1}^{2}+ \\ & \left| {{S}_{1}} \right|~{{{\hat{\chi }}}_{1}})+{{\zeta }_{1}}\left| {{S}_{1}} \right|+{{\vartheta }_{1}}\left| {{S}_{1}} \right|\left| {{\xi }_{1}} \right|+\frac{{{\varepsilon }_{1}}}{{{{\bar{p}}}_{1}}}{{{\hat{\zeta }}}_{1}}{{{\tilde{\zeta }}}_{1}}+ \\ & \frac{{{\varepsilon }_{2}}}{{{q}_{1}}}{{{\hat{\vartheta }}}_{1}}\tilde{\vartheta }{{~}_{1}}-{{\zeta }_{1}}\left| {{S}_{1}} \right|+\hat{\zeta }{{~}_{1}}\left| {{S}_{1}} \right|-{{\vartheta }_{1}}\left| {{S}_{1}} \right|\left| {{\xi }_{1}} \right|+ \\ & {{{\hat{\vartheta }}}_{1}}\left| {{S}_{1}} \right|\left| {{\xi }_{1}} \right|=-\left( {{\alpha }_{1}}S_{1}^{2}-\frac{{{\varepsilon }_{1}}}{{{{\bar{p}}}_{1}}}{{{\hat{\zeta }}}_{1}}{{{\tilde{\zeta }}}_{1}}-\frac{{{\varepsilon }_{2}}}{{{{\bar{q}}}_{1}}}{{{\hat{\vartheta }}}_{1}}{{{\tilde{\vartheta }}}_{1}} \right)\le -{{\alpha }_{1}}S_{1}^{2} \\ & -\frac{{{\nu }_{1}}}{2{{{\bar{p}}}_{1}}}\tilde{\zeta }_{1}^{2}-\frac{{{\nu }_{2}}}{2{{{\bar{q}}}_{1}}}\tilde{\vartheta }_{1}^{2}+\frac{{{\nu }_{3}}}{{{{\bar{p}}}_{1}}}\zeta _{1}^{2}+\frac{{{\nu }_{4}}}{{{{\bar{q}}}_{1}}}\vartheta _{1}^{2}, \\ \end{align}$ |
于是,可以得到
步骤2:在|S1|
| $\begin{align} & {{{\dot{V}}}_{1}}\le -\left( {{\alpha }_{1}}S_{1}^{2}+\frac{S_{1}^{2}}{{{\varepsilon }_{1}}}{{{\hat{\chi }}}_{2}} \right)+({{{\hat{\zeta }}}_{1}}+{{{\hat{\vartheta }}}_{1}}\left| {{\xi }_{1}}\left| ) \right|{{S}_{1}} \right|- \\ & \frac{{{\varepsilon }_{1}}}{{{{\bar{p}}}_{1}}}{{{\hat{\zeta }}}_{1}}{{{\tilde{\zeta }}}_{1}}-\frac{{{\varepsilon }_{2}}}{{{{\bar{q}}}_{1}}}{{{\hat{\vartheta }}}_{1}}{{{\tilde{\vartheta }}}_{1}}\le -{{\alpha }_{1}}S_{1}^{2}+{{\left( \frac{{{S}_{1}}}{\sqrt{{{\varepsilon }_{1}}}}{{{\hat{\chi }}}_{1}}-\frac{\sqrt{{{\varepsilon }_{1}}}}{2}~ \right)}^{2}}- \\ & \frac{{{\varepsilon }_{1}}}{{{{\bar{p}}}_{1}}}{{{\hat{\zeta }}}_{1}}{{{\tilde{\zeta }}}_{1}}-\frac{{{\varepsilon }_{2}}}{{{{\bar{q}}}_{1}}}{{{\hat{\vartheta }}}_{1}}{{{\tilde{\vartheta }}}_{1}}-\frac{{{\varepsilon }_{1}}}{4}\le -{{\eta }_{1}}{{V}_{1}}+{{\delta }_{2}}, \\ \end{align}$ |
其中,
从定理2.1可知控制器(13) 使子系统(10) 达到了一致有界。为了使系统达到有限时间稳定,在控制器中加入非线性反馈项-σ1 sign (S1)|S1|
| ${{u}_{22}}=-{{u}_{21}}-{{\sigma }_{1}}\text{sign}\left( {{S}_{1}} \right)\left| {{S}_{1}} \right|{{~}^{\frac{1}{2}}}。$ | (17) |
将式(17) 代入式(12),可得
| $J{{{\dot{S}}}_{1}}={{{\tilde{F}}}_{2}}-{{\alpha }_{1}}{{S}_{1}}-{{\sigma }_{1}}\text{sign}\left( {{S}_{1}} \right){{\left| {{S}_{1}} \right|}^{\frac{1}{2}}},$ | (18) |
其中,
定理2.2 考虑系统(18),在控制器(17) 和自适应律(14) 的作用下,滑模面S1将在有限时间内收敛到区域ǪS,然后跟踪误差θe和ωe也会在有限时间内分别收敛到Ǫθ和Ǫω,其中ǪS=max (ǪS1, ǪS2),Ǫθ=max (ε, εS),Ǫω=ǪS+k1Ǫθ+k2Ǫθr;ǪS1=
证明这里也分为两个步骤。
步骤1:先证明滑模面S1将在有限时间内收敛到区域ǪS。
考虑如下李雅普诺夫函数:
| ${{V}_{2}}=\frac{1}{2}S_{1}^{\text{T}}J{{S}_{1}},$ | (19) |
对其求导,并将式(18) 代入可得:
| ${{{\dot{V}}}_{2}}\le -({{\alpha }_{1}}S_{1}^{2}+{{\sigma }_{1}}{{\left| {{S}_{1}} \right|}^{~\frac{3}{2}~}})+\left| {{S}_{1}}{{\delta }_{3}} \right|。$ | (20) |
根据式(20),在|S1|>ǪS的情况下,
| ${{{\dot{V}}}_{2}}\le -{{\eta }_{2}}{{V}_{2}}-{{\eta }_{3}}V_{2}^{\frac{3}{4}~},$ |
其中
步骤2:再证明跟踪误差θe和ωe也会在有限时间内分别收敛到区域Ǫθ和Ǫω。
在|θe|≥ε的情况下,根据S1的表达式可得:
| $\begin{align} & {{\omega }_{e}}+{{k}_{1}}{{\theta }_{e}}+{{k}_{2}}\theta _{e}^{r}={{\varepsilon }_{1}}, \\ & \left| {{\varepsilon }_{1}} \right|\le {{Ǫ}_{S}}, \\ \end{align}$ | (21) |
| $\begin{align} & {{\omega }_{e}}+({{k}_{1}}-\frac{{{\varepsilon }_{1}}}{{{\theta }_{e}}}){{\theta }_{e}}+{{k}_{2}}\theta _{e}^{r}={{\varepsilon }_{1}}, \\ & {{\omega }_{e}}+{{k}_{1}}{{\theta }_{e}}+({{k}_{2}}-\frac{{{\varepsilon }_{1}}}{\theta _{e}^{r}})\theta _{e}^{r}={{\varepsilon }_{1}}, \\ \end{align}$ | (22) |
根据引理2.2,当满足条件k1-
前面已经得到,控制器(17) 保证了角速度误差在有限时间内收敛到小区域Ǫω。因此sin θe→0,cos θe→1。所以,动态子系统(11) 可以简化为
| $\left\{ \begin{array}{*{35}{l}} {{{\dot{x}}}_{e}}=v-{{v}_{r}}+{{\omega }_{r}}{{y}_{e}} \\ {{{\dot{y}}}_{e}}=-{{\omega }_{r}}{{x}_{e}} \\ m\dot{v}={{u}_{1}}+{{d}_{1}} \\ \end{array} \right.,$ | (23) |
令Ωe=xe-sign (ωr)ye,定义Φ=
现控制器设计如下:
| ${{S}_{au2}}=\left\{ \begin{array}{*{35}{l}} \mathit{\Omega }_{e}^{r},\rm{if}\quad {{{\bar{S}}}_{2}}=0\quad \rm{or}\quad {{{\bar{S}}}_{2}}\ne 0,\left| {{\mathit{\Omega }}_{e}} \right|\ge \varepsilon \\ {{\iota }_{3}}{{\mathit{\Omega }}_{e}}+{{\iota }_{4}}\rm{sign}\left( {{\mathit{\Omega }}_{e}} \right)\mathit{\Omega }_{e}^{2},\rm{if}\quad {{{\bar{S}}}_{2}}\ne 0,\left| {{\mathit{\Omega }}_{e}} \right|<\varepsilon \rm{ } \\ \end{array} \right.,$ | (24) |
其中,S2=Ωe+k1Ωe+k2Ωer。
将系统作变换得到如下式子:
| $m{{{\dot{S}}}_{2}}={{F}_{1}}+{{u}_{1}},$ | (25) |
其中,
| ${{E}_{\omega }}=\left\{ \begin{array}{*{35}{l}} r\ \Omega _{e}^{r-1},~\quad \rm{if}\quad {{{\bar{S}}}_{2}}=0~\ \rm{or}\quad {{{\bar{S}}}_{2}}\ne 0,\left| {{\mathit{\Omega }}_{e}} \right|\ge \varepsilon \\ {{\iota }_{3}}I+2{{\iota }_{4}}\,\rm{sign}\,\left( {{\mathit{\Omega }}_{e}} \right){{\mathit{\Omega }}_{e}},~\quad \rm{if}\quad {{{\bar{S}}}_{2}}\ne 0,\left| {{\mathit{\Omega }}_{e}} \right|<\varepsilon \\ \end{array} \right.。$ |
引理2.3 如果S2=S2=0,那么系统可在有限时间内达到Ωe=0,Φ=0。
此证明和引理2.2相似,故在此省略。
假设2.3 系统(25) 中,包含外部扰动和参数不确定性的集总扰动f1满足:|F1|≤ζ2+
实际中,外部扰动是有界的,移动机器人的质量也是有界的,参考轨迹的xr,yr,νr以及它们的导数也是有界的,因此假设2.3是合理的。于是,设计如下自适应控制器:
| ${{u}_{11}}=-{{\alpha }_{2}}{{S}_{2}}-{{u}_{adt}},$ | (26) |
其中,α2S2是反馈部分,自适应估计律uadt用来压制集总扰动的上界,其设计如下:
| ${{u}_{adt}}=\left\{ \begin{array}{*{35}{l}} \frac{{{S}_{2}}}{\left| {{S}_{2}} \right|}{{{\hat{\chi }}}_{2}},\quad if\quad \left| {{S}_{2}} \right|~{{{\hat{\chi }}}_{2}}>{{\varepsilon }_{2}} \\ \frac{{{S}_{2}}}{{{\varepsilon }_{2}}}\hat{\chi }{{~}^{2}},\quad if\quad \left| {{S}_{2}} \right|~{{{\hat{\chi }}}_{2}}\le {{\varepsilon }_{2}} \\ \end{array} \right.,$ | (27) |
其中ε2>0是待定设计参数,
| $\begin{align} & {{{\dot{\hat{\zeta }}}}_{2}}=-{{\varepsilon }_{3}}{{{\hat{\zeta }}}_{2}}+{{{\bar{p}}}_{2}}\left| {{S}_{2}} \right|, \\ & {{{\dot{\hat{\vartheta }}}}_{2}}=-{{\varepsilon }_{4}}{{{\hat{\vartheta }}}_{2}}+{{{\bar{q}}}_{2}}\left| {{S}_{2}} \right|\left| {{\xi }_{2}} \right|, \\ \end{align}$ | (28) |
其中,p2>0,q2>0以及ε3>0,ε4>0都是待定设计的参数。
定理2.3 根据动态系统(11),通过控制器(26) 以及自适应律(27),
此证明和定理2.1证明相似,故在此省略。
从定理2.3可知控制器(26) 成功使子系统(11) 达到了一致有界。为了使系统达到有限时间稳定,在控制器中加入非线性反馈项-σ2sign(S2)|S2|
| ${{u}_{12}}=-{{u}_{11}}-{{\sigma }_{2}}\text{sign}~\left( {{S}_{2}} \right)~{{\left| {{S}_{2}} \right|}^{\frac{1}{2}}},$ | (29) |
将式(31) 代入式(27),可得
| $J{{{\dot{S}}}_{2}}={{{\tilde{F}}}_{1}}-{{\alpha }_{2}}{{S}_{2}}-{{\sigma }_{2}}\text{sign}~\left( {{S}_{2}} \right)~{{\left| {{S}_{2}}~ \right|}^{\frac{1}{2}}},$ | (30) |
其中
定理2.4 考虑系统(30),在控制器(29) 和自适应律(27) 的作用下,滑模面S2将在有限时间内收敛到区域ρS,然后跟踪误差Ωe也会在有限时间内收敛到ρΩ。
其中
此证明和定理2.2证明相似,故在此省略。
定理2.5 考虑子系统(23),随着滑模面Ωe=xe- sign (ωr)ye收敛到ρΩ,跟踪误差xe和ye也会分别收敛到区域ρx和ρy。其中
证明考虑如下李雅普诺夫函数:
| ${{V}_{y}}=\frac{1}{2}y_{e}^{2},$ | (31) |
根据Ωe=xe- sign (ωr)ye以及Ωe收敛到ρΩ,可得|xe- sign(ωr)ye|<ρΩ,对式(31) 求导可得:
| ${{\dot{V}}_{y}}={{y}_{e}}{{\dot{y}}_{e}}=-{{y}_{e}}{{\omega }_{r}}{{x}_{e}}\le -\left| {{\omega }_{r}} \right|y_{e}^{2}+\left| {{y}_{e}} \right|{{б}_{\Omega }},$ | (32) |
从上述不等式可知,在|ye|>ρy的情况下,
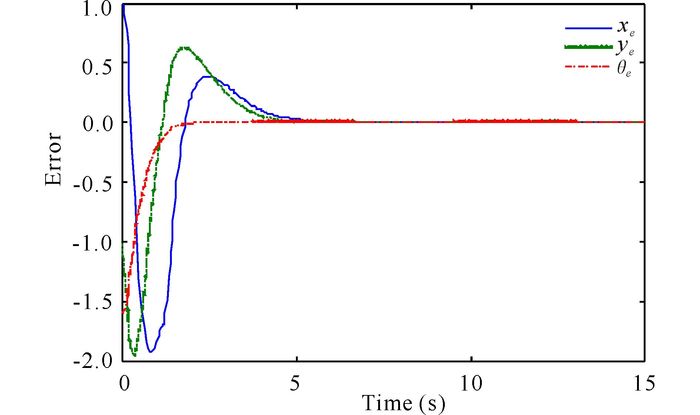
为了验证控制器的有效性,在MATLAB下构建如式(1) 和(2) 的轮式移动机器人模型,并进行仿真。轮式移动机器人模型的参数选择如下:b=0.3 m,r=0.1 m,J=2.5 kg·m2以及m=4 kg。集总扰动参数设置为d1=0.2ν+ω+ cos (te-t),d2=ν+0.3ω+ sin t。参考移动机器人的初始位置和姿态设置为(xr(0), yr(0), θr(0))=(4, 2,
|
图 2 轨迹跟踪误差 Fig.2 Tracking errors |
|
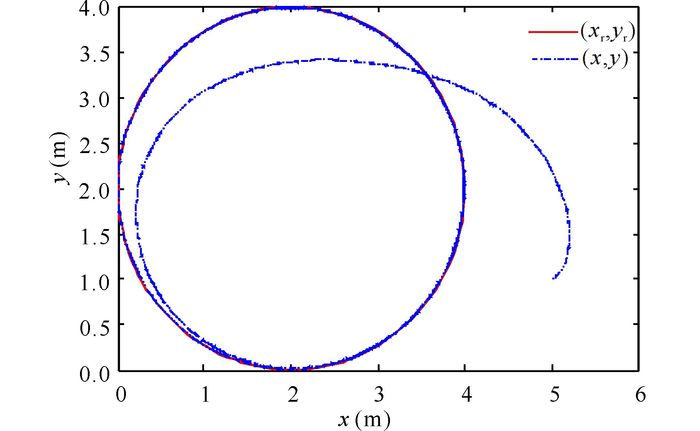
图 3 轨迹跟踪曲线 Fig.3 Trajectory tracking curve |

|
图 4 控制转矩 Fig.4 Control torques |
本研究针对轮式移动机器人动力学模型,提出了一种有限时间自适应轨迹跟踪控制方法。结合快速终端滑模控制策略和自适应技术,保证了跟踪误差在外界扰动和参数不确定性情况下收敛到一个任意小的区域内。最后,稳定性分析和仿真实验证明了本方法的有效性,这为不确定轮式移动机器人的轨迹跟踪控制研究提供了一种新的方法。
| [1] |
SHOJAEI K, SHAHRI A M, TARAKAMEH A. Adaptive feedback linearizing control of nonholonomic wheeled mobile robots in presence of parametric and nonparametric uncertainties[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(1): 194-204. DOI:10.1016/j.rcim.2010.07.007 |
| [2] |
ZENG W, WANG Q H, LIU F L, et al. Learning from adaptive neural network output feedback control of a unicycle-type mobile robot[J]. ISA Transactions, 2016, 61: 337-347. DOI:10.1016/j.isatra.2016.01.005 |
| [3] |
XIN L J, WANG Q L, SHE J H, et al. Robust adaptive tracking control of wheeled mobile robot[J]. Robotics and Autonomous Systems, 2016, 78: 36-48. DOI:10.1016/j.robot.2016.01.002 |
| [4] |
BAYAT F, MOBAYEN S, JAVADI S. Finite-time tracking control of nth-order chained-form non-holonomic systems in the presence of disturbances[J]. ISA Transactions, 2016, 63: 78-83. DOI:10.1016/j.isatra.2016.02.023 |
| [5] |
沈艳军, 胡俊波. 一类非线性系统连续非光滑自适应观测器设计[J]. 广西科学, 2015, 22(4): 421-424. SHEN Y J, HU J B. Continuous but nonsmooth adaptive observer design for a class of nonlinear systems[J]. Guangxi Sciences, 2015, 22(4): 421-424. |
| [6] |
CHEN W H, YANG W, ZHENG W X. Adaptive impulsive observers for nonlinear systems:Revisited[J]. Automatica, 2015, 61: 232-240. DOI:10.1016/j.automatica.2015.08.018 |
| [7] |
HUANG J S, WEN C Y, WANG W, et al. Adaptive stabilization and tracking control of a nonholonomic mobile robot with input saturation and disturbance[J]. Systems & Control Letters, 2013, 62(3): 234-241. |
| [8] |
黎艳, 陈武华. 具有饱和执行器的不确定脉冲系统的鲁棒镇定[J]. 西北师范大学学报:自然科学版, 2013, 49(6): 10-15. LI Y, CHEN W H. Robust stabilization of uncertain impulsive systems with saturating actuator[J]. Journal of Northwest Normal University:Natural Science, 2013, 49(6): 10-15. |
| [9] |
PARK B S, YOO S J, PARK J B, et al. A simple adaptive control approach for trajectory tracking of electrically driven nonholonomic mobile robots[J]. IEEE Transactions on Control Systems Technology, 2010, 18(5): 1199-1206. DOI:10.1109/TCST.2009.2034639 |
| [10] |
HOU Z G, ZOU A M, CHENG L, et al. Adaptive control of an electrically driven nonholonomic mobile robot via backstepping and fuzzy approach[J]. IEEE Transactions on Control Systems Technology, 2009, 17(4): 803-815. DOI:10.1109/TCST.2009.2012516 |
| [11] |
HWANG C L, WU H M. Trajectory tracking of a mobile robot with frictions and uncertainties using hierarchical sliding-mode under-actuated control[J]. IET Control Theory & Applications, 2013, 7(7): 952-965. |
| [12] |
DO K D, PAN J. Global output-feedback path tracking of unicycle-type mobile robots[J]. Robotics and Computer-Integrated Manufacturing, 2006, 22(2): 166-179. DOI:10.1016/j.rcim.2005.03.002 |
| [13] |
WANG Z P, GE S S, LEE T H.Adaptive neural network control of a wheeled mobile robot violating the pure nonholonomic constraint[C]//Proceedings of the 43rd IEEE Conference on Decision and Control.Nassau, Bahamas:IEEE, 2004:5198-5203.
|
| [14] |
ZHU X C, DONG G H, CAI Z X, et al. Robust simultaneous tracking and stabilization of wheeled mobile robots not satisfying nonholonomic constraint[J]. Journal of Central South University of Technology, 2007, 14(4): 537-545. DOI:10.1007/s11771-007-0104-2 |
| [15] |
BUCCIERI D, PERRITAZ D, MULLHAUPT P, et al. Velocity-scheduling control for a unicycle mobile robot:Theory and experiments[J]. IEEE Transactions on Robotics, 2009, 25(2): 451-458. DOI:10.1109/TRO.2009.2014494 |
| [16] |
OU M Y, SUN H B, LI S H.Finite time tracking control of a nonholonomic mobile robot with external disturbances[C]//31st Chinese Control Conference (CCC).Hefei:IEEE, 2012:853-858.
|
| [17] |
NAVIN C P, MIJA S J.Robust controller for trajectory tracking of a Mobile Robot[C]//IEEE International Conference on Intelligent Control and Energy Systems (ICPEICES).Delhi:IEEE, 2016:1-6.
|
| [18] |
李娜, 王汝凉, 陈超洋. 基于神经网络的一类非仿射非线性系统的H∞控制[J]. 广西科学, 2010, 17(4): 328-331. LI N, WANG R L, CHEN C Y. Robust H∞ control for a class of non-affine nonlinear systems with time-delay based on neural networks[J]. Guangxi Sciences, 2010, 17(4): 328-331. |
| [19] |
BOUKENS M, BOUKABOU A. Design of an intelligent optimal neural network-based tracking controller for nonholonomic mobile robot systems[J]. Neurocomputing, 2017, 226: 46-57. DOI:10.1016/j.neucom.2016.11.029 |
| [20] |
LU K F, XIA Y Q. Adaptive attitude tracking control for rigid spacecraft with finite-time convergence[J]. Automatica, 2013, 49(12): 3591-3599. DOI:10.1016/j.automatica.2013.09.001 |
| [21] |
KHALIL H K. Nonlinear systems[M]. 3rd edition. New York: Prentice-Hall, 2002.
|
 2017, Vol. 24
2017, Vol. 24 


