2. 广西大学计算机与电子信息学院, 广西 南宁 530004;
3. 广西高校并行分布式计算技术重点实验室,广西 南宁 530004
2. School of Computer, Electronics and Information in Guangxi University, Nanning, Guangxi, 530004, China;
3. Guangxi Colleges and Universities Key Laboratory of Parallel and Distributed Computing Technology, Nanning, Guangxi, 530004, China
【研究意义】无线Mesh网络[1](WMN)是无线网络核心技术的代表之一,成功地解决关于无线网络通讯过程中“最后一公里”的接入问题。WMN网络是一种具有自管理、自组织、多跳转发的无线网络,具有覆盖范围大、扩展性好、可靠性高等特点,被广泛应用于诸多领域。WMN网络的核心由Mesh路由器节点组建的骨干网络和作为用户节点的终端网络组成,骨干网络架构中的路由器节点负责外部网络与用户节点之间的链接访问。然而,由于各节点之间通过无线信号链接进行通讯,并且共享同一个无线通讯信道,因此在通信过程中彼此之间产生信号干扰。各节点之间如何建立连接、保证网络通畅、降低网络通讯信号干扰是WMN网络拓扑控制的研究目标。对WMN网络拓扑控制的优化程度直接影响到网络整体性能的有效发挥和利用。对拓扑控制技术进行优化,以降低网络通讯时的信号干扰,进而使网络整体性能得到一定的提高。【前人研究进展】目前,对WMN网络的拓扑控制尚处于理论研究阶段。无线网络拓扑控制技术主要由集中式和分布式两类组成[2]。集中式拓扑控制技术在网络中设置中心节点,收集汇总全局网络信息并建立一个强连通拓扑结构网络。如CONNECT和BICONN-AUGMENT[3]拓扑控制技术,主要解决网络中节点的数据发送功率最小化问题以及同构网1-连通相关问题;分布式拓扑控制在网络中不设置中心节点,要求网络各个节点与邻节点交互信息,并根据所收集的网络信息自动建立局部网络拓扑结构。如LINT和LILT[4]拓扑控制技术。CBTC[5]拓扑控制技术要求每个节点有N个扇区,通讯时逐渐提高节点数据发送功率,当达到功率最大或所有扇区中至少能建立一个通讯链路为止,但该技术的网络中节点平均链路连接度和数据发送功率偏高;基于Delaunay三角网的拓扑优化算法ODADT[6]主要是基于生成树建立后优化最小链路角度,以对网络拓扑结构做进一步优化。但该网络节点链接存在舍近求远的缺点,因为增加了网络节点通讯过程中产生的干扰。【本研究切入点】近年来,计算几何在WMN网络拓扑研究中的应用也越来越受到关注,尤其是临近图,如最小生成树MST图[7]、GG图[8]、RNG图[9]、DT图[10]等。受此启发,本研究针对基于Delaunay三角网的WMN网络特点以及拓扑控制存在的问题,提出一种改进的拓扑优化控制算法。【拟解决的关键问题】通过优化节点通信链路角度,使其相对最大,降低网络拓扑复杂度,并采用定向通讯机制降低通讯链路之间信号干扰。
1 WMN网络的不足及改进 1.1 WMN网络不足之处基于Delaunay三角网的WMN网络存在复杂性高、维护信息量大、平均连接度高、信道干扰严重等缺点。由于骨干网络中网关节点的存在,使得网络节点与外网的数据流汇聚网关,从而导致网关节点数据聚集现象,数据信号之间产生较大干扰,继而增加数据的丢包率,影响网络整体性能的发挥。其根本原因在于WMN网络拓扑结构的复杂度高,导致网络中各个节点存在多条链路,且每条链路之间的角度较小,在定向通讯时,链路之间产生的干扰较为严重,从而导致网络整体性能下降。
李文阁[6]提出的ODADT拓扑优化算法,能优化基于Delaunay三角网的WMN网络拓扑结构,降低网络拓扑复杂度以及节点通讯时彼此造成的信道干扰,在一定程度上提高了WMN网络的整体性能。但是以基于跳数的最小生成树为基础进行角度优化,使得网络拓扑存在随机性以及舍近求远的链路连接,从而导致节点所拥有的链路角度相对较小,对于定向通讯的WMN网络来说依然会造成很大的干扰,进而影响网络整体性能。由此可见,针对基于Delaunay三角网的WMN网络拓扑控制与优化对于网络整体性能的提升和改善起着十分重要的作用。
1.2 改进方案针对基于Delaunay三角网的WMN网络的缺点、ODADT拓扑优化算法的不足以及节点链路之间的夹角较小所导致的信号干扰问题,在保证网络连通以及节点最大连接度约束条件下,控制节点链路之间的夹角以降低通讯干扰,提出一种基于链路角度最优化的拓扑优化算法(Link Angle Optimization Algorithms based on Delaunay Triangulation Network,LAOADT),在满足约束条件的同时,保证节点链路之间的角度相对最大。这样既保证了网络的连通性,又避免出现因舍近求远链路的存在而导致的链路夹角较小, 以及通讯时对其他节点产生严重信号干扰的现象。
2 LAOADT算法的优化 2.1 优化思想在基于Delaunay三角网的Mesh网络中,由于钝角三角形的存在,致使钝角边对应节点的链路夹角相对较小。删除钝角边不但可以增加节点链路之间的夹角角度,同时也保证了节点之间的连通。因此,首先对Delaunay三角形网络的钝角边进行删除优化,优化后的网络拓扑依然保持连通性;其次,对优化后的网络拓扑,在满足节点最大连接度约束条件的同时,进一步优化节点链路,依据节点所拥有链路分布情况的不同采取不同的链路选择方式。链路的分布情况可分为小于180°扇区,大于180°扇区以及360°全扇区。根据节点所拥有标准边个数以及链路的分布情况选择链路,从而使链路角度达到相对最大;最后,对优化后的拓扑结构进行检测,得到优化拓扑。
2.2 算法描述假设每一个链路的最大度为3,各节点链路存在3种状态:不可删除边状态(allow=0),保留边状态(allow=1),可删除边状态(allow=2)。不可删除边作为标准边选择其他边,被选择的边为保留边。节点链路分布情况为小于180°扇区(area=0),大于180°扇区(area=1),360°全扇区(area=2)。V(n)表示网络的节点集合,G(n)表示网络的拓扑结构。
算法的伪代码如下:
初始化V(n)点集;
Delaunay(V(n),G(n));
Delete_long_edge(G(n));
For(every node u in V(n)){
If(allow_num(u)==0){ /*没有标准边*/
If(area(u)==0){
Select_two_edge()
}
Else{
Select_three_edge();
}
}
Else if (allow_num(u)==1){
/*以不可删除边作为标准边去选择边*/
If(area(u) ==0)
Select_one_edge();
Else If(area(u)==1)
Select_one_edge();
Else
Select_two_edge();
}
Else if (allow_num(u)==2){
……
}
Else
Select_zero_edge();
}
输出优化拓扑网络G(n).
3 模拟实验与分析对LAOADT算法进行模拟实验并对模拟实验结果进行数据统计对比。利用C++程序语言搭建的拓扑控制实验平台进行网络优化,并根据优化结果在NS2中进行模拟实验。实验模拟场景为500 m×500 m,假设每一个节点的通讯范围相同为150 m,定向天线的个数为3个,每一个定向天线角度为120°。
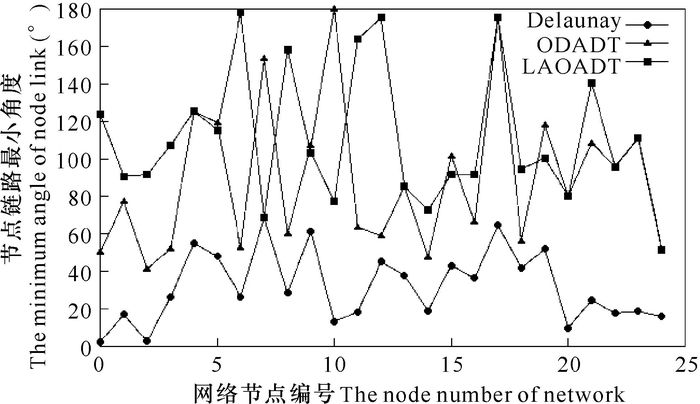
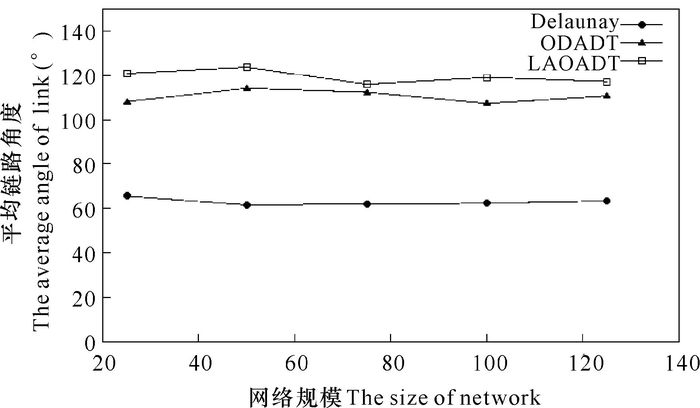
图 1表示同一网络规模,不同拓扑控制下节点链路最小角度的比较情况。图 2表示在不同网络节点规模下,网络中各节点平均链路角度对比情况。通过与图 1数据统计结果对比可知,由于网络复杂度高,节点链路相对最多,从而导致了Delaunay三角网络中节点的链路角度最小;LAOADT和ODADT两种拓扑的链路角度相对较大,但是由于LAOADT拓扑采取链路角度最优化处理,因此相比于ODADT拓扑而言,节点链路最小角度整体相对较大;通过图 2数据对比可知,随着网络规模的增加,3种拓扑网络的平均链路角度变化相对平稳,但可以看出LAOADT拓扑的链路角度最大,ODADT拓扑次之,Delaunay拓扑最小。由此可见,基于链路角度最优化的LAOADT拓扑确实在一定程度上提升了节点链路角度,从而证明了LAOADT优化算法的可行性。
|
图 1 同一网络不同节点链路角度对比 Fig.1 The link angle contrast of different nodes in the same network |
|
图 2 不同网络节点平均链路角度对比 Fig.2 The average link angle contrast of different network nodes |
图 3表示在不同网络规模下,不同网络拓扑结构的丢包率对比情况。通过图 3的丢包率对比可以看出,当网络规模较小时,由于网络节点数目较少,相互影响较小,因此丢包率较低,从而导致3个拓扑网络中节点平均丢包率对比度不够明显。随着网络节点规模的增加(75个网络节点以上),网络拓扑复杂度也增加,同时由于Delaunay三角网络中节点间链路角度过小,节点链路之间的干扰问题凸显,导致网络的丢包率开始大幅增加。然而由于采用了拓扑优化技术,使ODADT和LAOADT拓扑中节点链路减少,简化了拓扑复杂度,增加了节点链路之间的夹角,降低了通信链路之间的干扰,相对于Delaunay三角网络来说,丢包率增加的幅度迟缓。LAOADT算法通过对节点间链路角度的优化处理,同ODADT算法相比,当网络节点规模增加时,能保证节点间链路角度最大化,使信道干扰相对较低,使得丢包率增长相对缓慢。由此可知,LAOADT算法在优化节点链路角度的同时,也使得网络丢包率在一定程度上得到改善。

|
图 3 丢包率对比 Fig.3 The packet loss rate contrast |
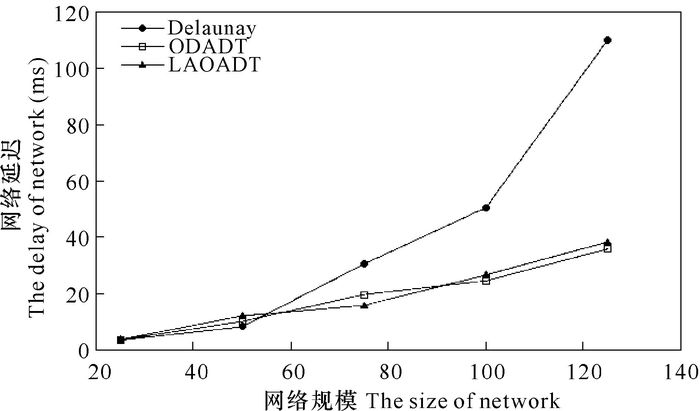
图 4显示不同网络节点规模下,网络中各节点的平均延迟对比情况。通过对比结果可知,在网络节点规模较小时(50节点以内),由于节点数较小、跳数少、复杂度较低、路由相对简单、网络之间的干扰相对较小,使各拓扑网络中节点的平均延迟差异性较小。但随着网络节点规模的增加,基于Delaunay三角网络的Mesh网络拓扑复杂度增加,节点间通信链路增多,对通信链路产生的信号干扰增强,导致网络数据丢包率以及数据传输延迟增加。LAOADT算法和ODADT算法通过拓扑控制技术优化,在保证网络连通性的同时,减少了诸多链路连接,也相应降低了干扰,使得两种拓扑网络延迟差异性较小。但数据延迟的增加相对Delaunay三角网络来说比较缓慢,也有一定程度的改善。
|
图 4 延迟对比 Fig.4 The delay contrast |
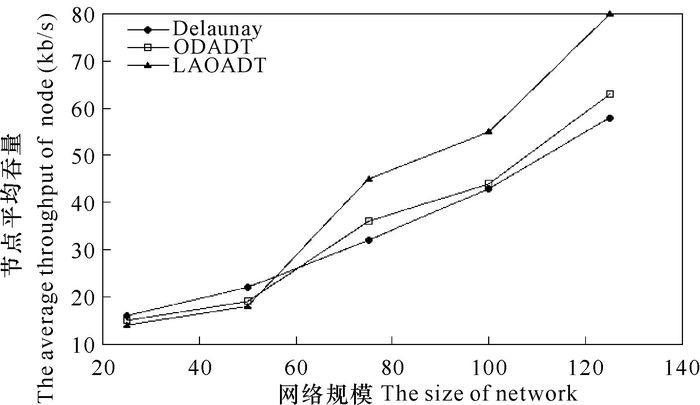
图 5表示在不同网络节点规模下,不同网络拓扑结构中网络节点平均吞吐量的对比情况。可以看出,网络节点规模增大时,LAOADT网络节点平均吞吐量较好,当网络节点规模相对较小时网络中节点的平均吞度量相对较低。当网络节点规模较小时,各网络中节点的链路数低,节点通讯链路相互干扰较低,此时Delaunay三角网络的连通性以及网络节点的平均吞吐量相对较高。随着网络节点规模的增加,Delaunay三角网络中节点平均吞吐量相对于其他两个拓扑网络增长率最小。这是因为Delaunay三角网络随网络节点规模的增大,复杂度也在剧增,网络中节点之间的干扰、延迟、丢包率等相对增加,致使网络的整体性能下降。采用了拓扑控制技术的LAOADT和ODADT两个网络,在保证网络连通的同时,有效地降低了节点通讯链路间信道干扰,使网络节点平均吞吐量整体得到提升。随着网络节点规模的逐渐增大,同ODADT相比,LAOADT网络节点的平均吞吐量得到了提高,使得网络的整体性能也得到一定程度优化。
|
图 5 吞吐量对比 Fig.5 The throughput contrast |
针对基于Delaunay三角网络的WMN网络的特点以及拓扑控制存在的问题,提出一种基于节点链路角度最优化的拓扑优化控制算法LAOADT。实验对比结果表明,在满足约束条件下,该拓扑优化控制算法不但使节点链路之间角度控制在相对最大范围,减小了定向通讯时信道的干扰,同时也改善了WMN网络的丢包率、延迟、吞吐量等性能,从而进一步提高了WMN网络的整体性能。这验证了基于节点链路角度最优化的拓扑优化控制方案的可行性和实用性。下一步将继续研究WMN网络中多信道分配算法以及在北部湾海洋研究中的技术应用等问题,进一步优化WMN网络在应用领域的整体性能。
| [1] |
AKYILDIZ I F, WANG X D, WANG W L. A survey on wireless mesh networks[J]. Computer Networks, 2005, 47(4): 445-487. DOI:10.1016/j.comnet.2004.12.001 |
| [2] |
叶宁. Ad Hoc网络拓扑控制算法的设计与仿真[D]. 沈阳: 东北大学, 2008. YE N.Design and simulation of a topology control algorithm for Ad Hoc networks[D].Shenyang:Northeastern University, 2008. |
| [3] |
BEN-OTHMAN J, BESSAOUD K, BUI A, et al. Self-stabilizing algorithm for efficient topology control in Wireless Sensor Networks[J]. Journal of Computational Science, 2013, 4(4): 199-208. DOI:10.1016/j.jocs.2012.01.003 |
| [4] |
BEN-OTHMAN J, BESSAOUD K, BUI A, et al.Self-stabilizing algorithm for energy saving in Wireless Sensor Networks[C]//2011 IEEE Symposium on Computers and Communications (ISCC).Kerkyra:IEEE, 2011:68-73.
|
| [5] |
HE L N. Research on train control system based on communications[J]. Applied Mechanics and Materials, 2013, 253-255: 1427-1430. |
| [6] |
李文阁. 基于Delaunay图形的无线Mesh骨干网络部署优化研究[D]. 南宁: 广西大学, 2011. LI W G.Research on topology optimization about wireless mesh backbone network based on Delaunay triangulation[D].Nanning:Guangxi University, 2011. |
| [7] |
NEOGI S G. Routing method for wireless mobile ad hoc networks using pascal graph topology[J]. International Journal of Research in Computer Engineering & Electronics, 2013, 1(3): 1101-1109. |
| [8] |
SHIRANI R, ST-HILAIRE M, KUNZ T, et al.The performance of greedy geographic forwarding in unmanned aeronautical ad-hoc networks[C]//2011 Ninth Annual Communication Networks and Services Research Conference (CNSR).Ottawa:IEEE, 2011:161-166.
|
| [9] |
WANG H C, WOUNGANG I, LIN J B, et al. Revisiting relative neighborhood graph-based broadcasting algorithms for multimedia ad hoc wireless networks[J]. The Journal of Supercomputing, 2012, 62(1): 24-41. DOI:10.1007/s11227-011-0662-9 |
| [10] |
AICHHOLZER O, FABILA-MONROY R, HACKL T, et al. Blocking Delaunay triangulations[J]. Computational Geometry, 2013, 46(2): 154-159. DOI:10.1016/j.comgeo.2012.02.005 |
 2017, Vol. 24
2017, Vol. 24 


