2. 广西高校复杂系统与智能计算重点实验室,广西 南宁 530006
2. Guangxi Higher School Key Laboratory of Complex Systems and Intelligent Computing, Nanning, Guangxi, 530006, China
Data clustering is the process of grouping together similar multi-dimensional data vectors into a number of clusters.Clustering algorithms have been applied to a wide range of problems, including exploratory data analysis, data mining[1], image segmentation and mathematical programming[2].Research in exact algorithms, heuristics and meta-heuristics for solving combinatorial optimization problems is increasingly relevant as data science grapples with larger and more complex data sets[3].
Clustering algorithms can be grouped into two main classes of algorithms, namely hierarchical and partitioned.In hierarchical clustering, the number of clusters need not be specified a prior but by partitioned methods it should be determined.As a result, hierarchical methods cannot always separate overlapping clusters.Additionally, hierarchical clustering is static and points committed to a given cluster in the early stages cannot be moved between clusters[4].While the partitioned clustering divide in two categories:Crisp clustering where each data point belongs to just one cluster and fuzzy clustering where every data point belongs to every cluster to some degree[5-6].This paper adopts the first method:Crisp clustering.
Several optimization techniques have been proposed to increase the performance of clustering algorithms.Nikam et al have proposed an efficient hybrid evolutionary algorithm based on combining ACO and SA for clustering problem.In 1991, Zamani et al[7] have presented Ant Colony Optimization (ACO) algorithm based on the behavior of ants seeking a path between their colony and a source of food.Then Shelokar et al[8]solved the clustering problem using the ACO algorithm.Kennedy and Eberhart[9] have proposed Particle Swarm Optimization (PSO) algorithm which simulates the movement of organisms in bird flock or fish school in 1999.
Multi-verse Optimization (MVO) is one of the meta-heuristic methods proposed by Mirjalili[10] in 2016.The main inspirations of that algorithm are based on three concepts in cosmology.They are white hole, black hole, and wormhole.The mathematical models of these three concepts are developed to perform exploration, exploitation and local search.Exploitation and exploration are two major issues when designing a meta-heuristic.The MVO algorithm has many advantages such as a simple structure, immediately accessible for practical application, ease of implementation and speed to acquire solution.So it has captured much attention and has been successfully applied to a wide range of practical optimization problems including real engineering problems.This paper presents a new optimization approach to data clustering based on the MVO and analysis of consumption structure of Chinese urban residents based on Dynamic Clustering Method rate.
1 Related workRecently, bioinspired stochastic search methods, especially the algorithms based on population behavior and self-organization of social insects and animals, known as Swarm Intelligence algorithms, have been considered as an emerging alternative to traditional clustering methods, because are very suitable to deal with global optimization problems.These algorithms are effective, robust and adaptive, producing almost optimal solutions through mechanisms of evolution.Numerous studies have been performed concerning clustering using SI.Most of them employ Particle Swarm Optimization (PSO), the simplest SI algorithm, which is the SI paradigm that has received widespread attention in research.Nowadays, many scientists work on data categorizing in the clusters with different manners such as meta-heuristic algorithms that they are mostly used for solving optimization problems[11].MVO algorithm for clustering is to evolve a set of possible clusters centroids (candidate solutions) for determining an almost optimal partitioning of a dataset.An important advantage of MVO algorithm applied to data clustering task is their ability to handle local minima by recombination and comparison of various candidate solutions.
Multi-verse Optimization (MVO) Algorithm is a novel meta-heuristic algorithm inspired by the phenomenon of multi-verse.The algorithm mainly contains transfer progress and position update progress.The algorithm has advantages such as simple structure, less parameters, easy to understand, excellent search ability.In recent years, Multi-verse optimization (MVO) algorithm has received more and more attention of domestic and foreign scholars, and has been successfully applied to various fields.In view of the low accuracy of traditional methods, efficiency is not high and easy to fall into local optimum in solving clustering problems.This paper adopts the MVO algorithm to solve clustering problems.Simulation results validate that the MVO algorithm is feasible and efficient to solve the clustering problems.
In this paper, data clustering problem is solved by population based algorithm (Multi-verse Optimization Algorithm).For explaining the evaluation process explicitly, we suppose that given data set D should be divided into K subsets.And the dimension of individual of data set D is m.In order to optimize the coordinates of centers of K subsets, it is easy to find that the dimension of solution should be K * m.The individual in the population can be described as s= c1, c2, …, ck.A great classification should minimize the sum of distances value.So we should try to minimize the distance between individual di and the center (cj) of subset it belongs to.Finally, the proposed algorithm aims at minimizing the objective function, which can be expressed as following:
| $f\left( D,C \right)=\sum\limits_{i=1}^{n}{\text{min}}\{\ \left\| {{d}_{i}}-{{c}_{k}} \right\|k=1,2,\cdots ,K\}$ |
Where D=(d1, d2, …, dn) is the given data set, C=(c1, c2, …, ck)is the centers of subsets (G1, G2, …, Gk).
2 Multi-verse optimization algorithmMulti-verse Optimization Algorithm (MVO) is inspired by the theory of multi-verse in physics, Three main concepts of the multi-verse theory (white hole, black hole, and wormhole) (see Fig. 1) are mathematically modeled to construct the MVO.We utilize the concepts of white hole and black hole in order to explore search spaces[12] by MVO.In contrast, the wormholes assist MVO in exploiting the search spaces.We assume that each solution is analogous to a universe and each variable in the solution is an object in that universe.In addition, we assign each solution an inflation rate, which is proportional to the corresponding fitness function value of the solution.We also use the term time instead of the iteration since it is a common term in multi-verse theory and cosmology.The following rules are applied to the universes of MVO:
(1) The higher inflation rate, the higher probability of having white hole.
(2) The higher inflation rate, the lower probability of having black holes.
(3) Universes with higher inflation rate tend to send objects through white holes.
(4) Universes with lower inflation rate tend to receive more objects through black holes.
(5) The objects in all universes may face random movement towards the best universe via wormholes regardless of the inflation rate.
(6) In order to mathematically model the white/black holes tunnels and exchange the objects of universes, we utilized a roulette wheel mechanism.
At the each iteration, we sort the universe based of their inflation rates and chose one of them by the roulette wheel to have a white hole[15].The following steps are done in order to do this.Assume that
| $u=\left[ \begin{matrix} x_{1}^{1} & x_{1}^{2} & \cdots & x_{1}^{d} \\ x_{1}^{2} & x_{2}^{2}~ & \cdots & x_{2}^{d} \\ \vdots & \vdots & \vdots & \vdots \\ x_{n}^{1} & x_{n}^{2} & \cdots & x_{n}^{d} \\ \end{matrix} \right]~,$ |
where d is the number of variables and n is the number of universes.
| $x_{i}^{j}=\left\{ \begin{array}{*{35}{l}} x_{k}^{j} & {{r}_{1}}<NI\left( {{U}_{i}} \right) \\ x_{i}^{j} & {{r}_{1}}\ge NI\left( {{U}_{i}} \right) \\ \end{array} \right.,$ |
where xij indicates the jth variable of the ith universe, Ui shows the ith universe, NI(Ui) is normalized inflation rate of the ith universe, r1 is a random number in (0, 1), xkj indicates the jth variable of kth universe selected by a roulette wheel selection mechanism.Procedure of the basic MVO is as follows:
| Table |
To provide local changes for each universe and have high probability of improving the inflation rate using wormholes, assuming that wormhole tunnels are always established between a universe and the best universe formed so far.The mechanism is as follows:
| $x_{i}^{j}=\left\{ \begin{array}{*{35}{l}} {{X}_{j}}+TDR*\left( \left( u{{b}_{j}}-l{{b}_{j}} \right)*{{r}_{4}}+l{{b}_{j}} \right) & {{r}_{3}}<0.5 \\ {{X}_{j}}-TDR*\left( \left( u{{b}_{j}}-l{{b}_{j}} \right)*{{r}_{4}}+l{{b}_{j}} \right) & {{r}_{3}}\ge 0.5 \\ \end{array}, \right.$ |
where Xj indicates the jth variable of the best universe formed so far; Travelling Distance Rate(TDR) (in Fig. 2) is a coefficient; Wormhole Existence Probability(WEP) is another coefficient; lbj is the lower bound of jth variable; ubj is the upper bound of jth variable, r2, r3, r4 are random numbers chosen from (0, 1).Here is the random number from 0 and 1 of the two numbers.Wormhole Existence Probability (WEP) and Travelling Distance Rate (TDR).The former coefficient is for defining the probability of wormhole's existence in universes.It is required to increase linearly over the iterations in order to emphasize exploitation as the progress of optimization process.Travelling distance rate is also a factor to define the distance rate (variation) that an object can be teleported by a wormhole around the best universe obtained so far.In contrast to WEP, TDR is increased over the iterations to have more precise exploitation/local search around the best obtained universe.
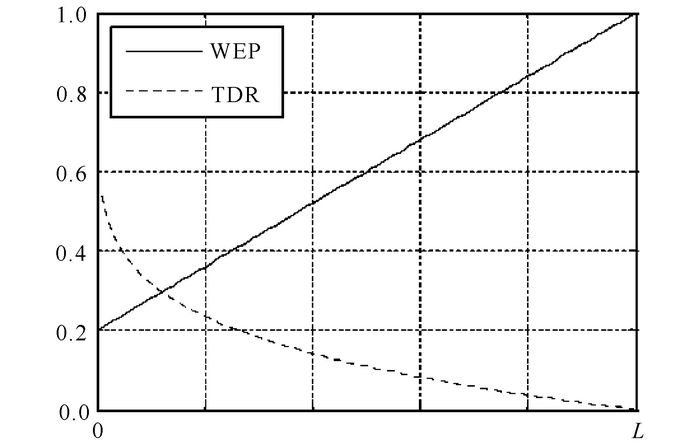
|
Fig.2 WEP versus TDR |
| $\text{WEP}=\text{min}+l*\left( \frac{\text{max}-\text{min}}{L} \right),$ |
min(minimum)=0.2, max(maximum)=1, l is the current iteration, L shows the maximum iterations.
| $\text{TDR}=1-\text{ }\frac{{{l}^{~\frac{1}{p}~}}}{{{L}^{~\frac{1}{p}~}}},$ |
Where p defines the exploitation accuracy over the iterations.In equals 6 is defined the exploitation accuracy over the iterations.The higher p, the sooner and more accurate exploitation/local search.
Procedure of the basic MVO is as follows:
| Table |
All of the algorithms are implemented in MATLAB R2012a.The algorithms are run on the same machine with AMD A10-6700 CPU with Radeon (tm) HD Graphics @ 3.70 GHz, 4.00 GB RAM and Windows 7 Operating System.
3.2 Comparison of each algorithm performanceThe proposed Multi-verse optimization algorithm compared with mainstream swarm intelligence algorithms, CS[16-19], PSO[20-21], ABC[22-24], respectively using the mean and standard deviation to compare their optimal performance.The setting values of algorithm control parameters of the mentioned algorithms are given below.
CS setting:pa=0.25 have been used as recommended in, the population size is 50.
PSO setting:weight factor ω=0.729 8, c1=c2=1.496 2, the population size is 50.
ABC setting:limit = 5D has been used as recommended in, the population size is 50.
MVO setting:min is the minimum (0.2 in this paper), max is the maximum (1 in this paper), l indicates the current iteration and L shows the maximum iterations.p (In this paper equals 6) defines the exploitation accuracy over the iterations.The higher p, the sooner and more accurate exploitation/local search.The population size is 50.And the maximum generations of all algorithms are set 1 000.
In this section, eight data sets are selected to testify the effectiveness of the proposed algorithm, including two artificial data sets and six real-life data sets (selected from the UCI machine learning repository).There are artificial set one, artificial set two, Iris, Contraceptive Method Choice (CMC), Statlog (Heart), Balance Scale, Haber man's Survival, Wine.
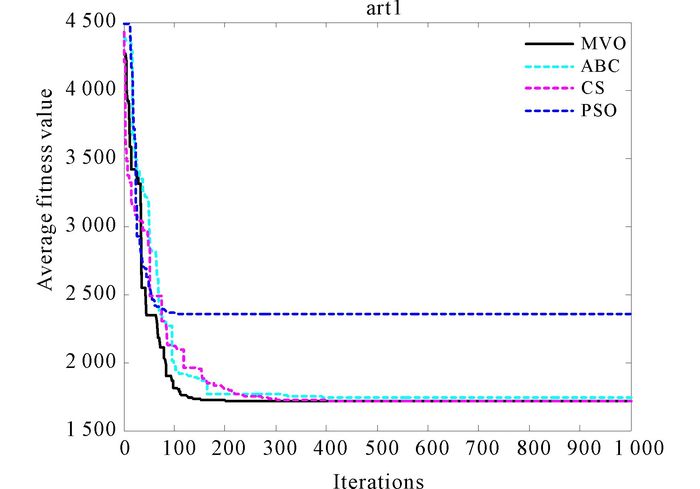
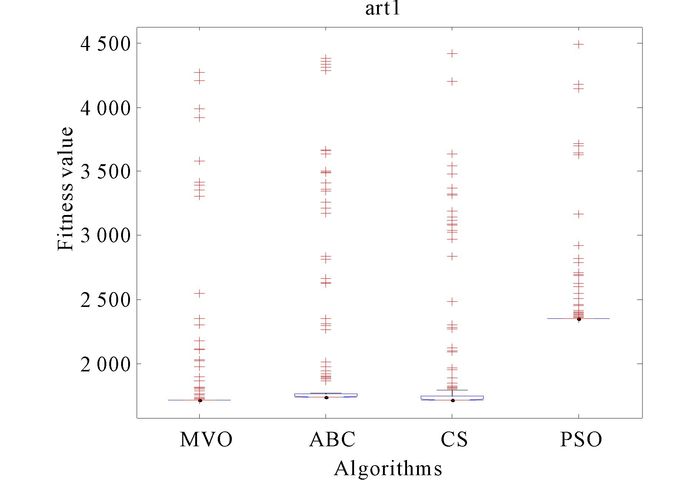
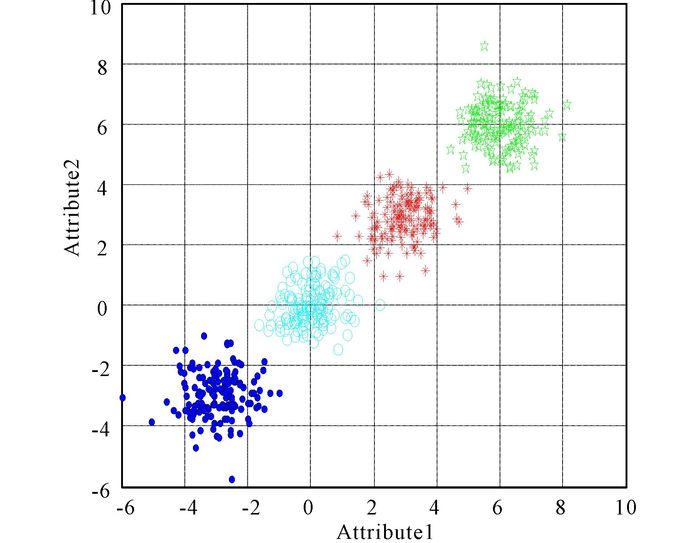
3.2.1 Artificial data set oneArtificial data set one (N=250, d=3, K=5).This is a three-featured problem with five classes, where every feature of the classes is distributed according to Class 1-Uniform (85, 100), Class 2-Uniform (70, 85), Class 3-Uniform (55, 70), Class 4-Uniform (40, 55), Class 5-Uniform (25, 40).The clustering result of MVO for art1 in Fig. 3.And the convergence curves of algorithms are shown in Fig. 4.In Fig. 5, it is the result of anova test for artificial data set one.

|
Fig.3 The clustering result of MVO for art1 |
|
Fig.4 The convergence curves of algorithms for art1 |
|
Fig.5 The anova test of algorithms for art1 |
In Fig. 3 every color represents one class.Class colored green and class colored red are not mixed together.And others are the same.Four convergence curves can be seen in Fig. 4, which is the comparison for artificial data set one.We can discover that the curve of MVO is much smoother than other algorithms expect PSO.And its convergence speed is faster.Fig. 5 is the anova test for data set art1.We can find that the stability of MVO is well.
3.2.2 Artificial data setArtificial data set two (N=600, d=2, K=4).This was a two-featured problem with four unique classes.A total of 600 patterns were drawn from four independent bivariate normal distributions, where classes were distributed according to:
| ${{N}_{2}}(\mu =\left( \begin{matrix} {{m}_{i}} \\ 0 \\ \end{matrix} \right),\sum \left[ \begin{matrix} 0.5 & 0.05 \\ 0.05 & 0.5 \\ \end{matrix} \right]),$ |
where i=1, 2, 3, 4, m1=-3, m2=0, m3=3, m=6.μ and ∑ being mean vector and covariance matrix, respectively[22].The clustering result of MVO for art2 in Fig. 6.And the convergence curves of algorithms are shown in Fig. 7.In Fig. 8, it is the result of anova test for artificial data set two.
|
Fig.6 The clustering result of MVO for art2 |
|
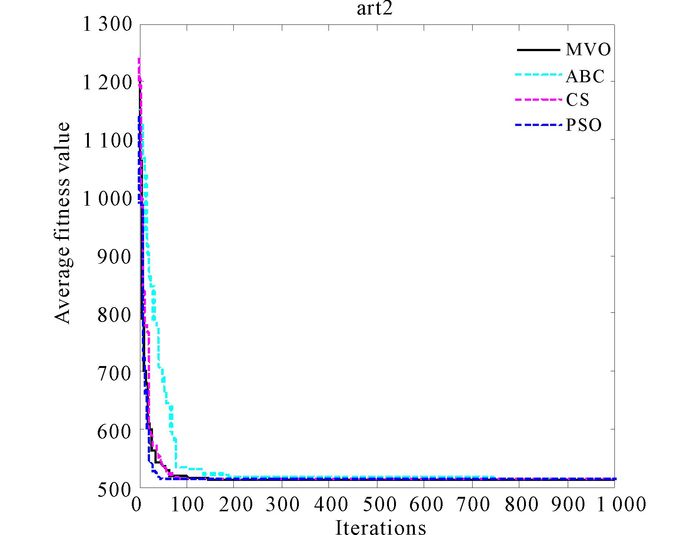
Fig.7 The convergence curves of algorithms for art2 |
|
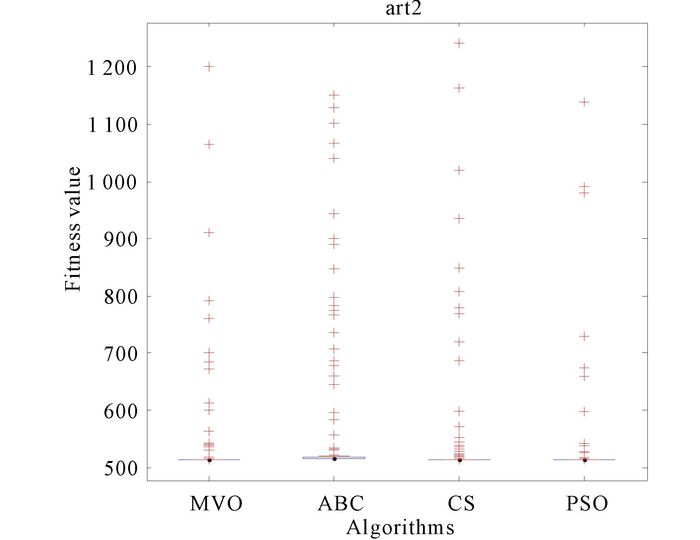
Fig.8 The anova test of algorithms for art2 |
Four convergence curves for artificial data set two are shown in Fig. 7.The curve of MVO is smoother than ABC and CS can be discovered easily.Faster convergence speed of MVO can be found as well as PSO.Fig. 8 shows that MVO has a high degree of stability.And four convergence curves for artificial data set two are shown in Fig. 7.The curve of MVO is smoother than others can be discovered easily.Faster convergence speed of MVO can be found as well.Fig. 8 shows that MVO has a high degree of stability.
3.2.3 Data set IrisIris data (N=150, d=4, K=3):This data set with 150 random samples of flowers from the iris species setosa, versicolor, and virginica collected by Anderson.From each species there are 50 observations for sepal length, sepal width, petal length, and petal width in cm.This data set was used by Fisher in his initiation of the linear-discriminant-function technique.The clustering result of MVO for Iris is in Fig. 9.And the convergence curves of algorithms are shown in Fig. 10.In Fig. 11, it is the result of anova test for Iris.
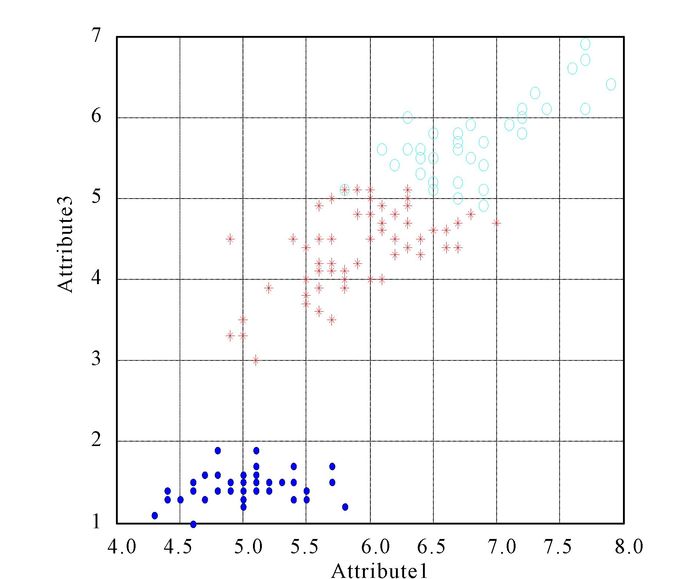
|
Fig.9 The clustering result of MVO for Iris |
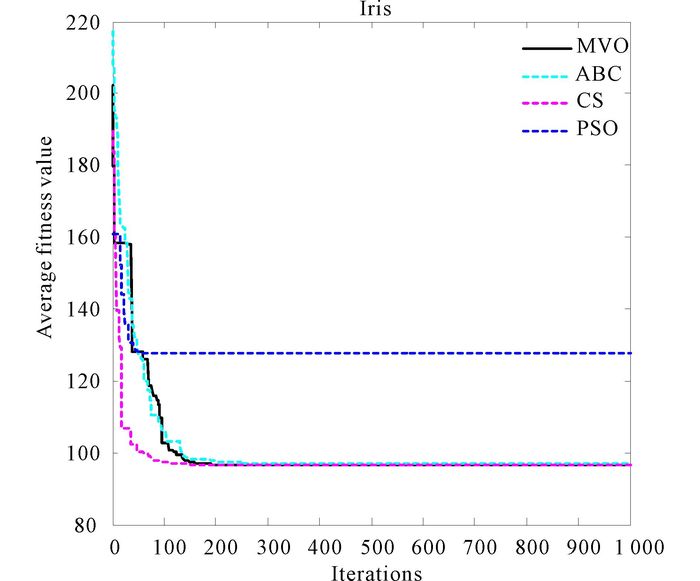
|
Fig.10 The convergence curves of algorithms for Iris |
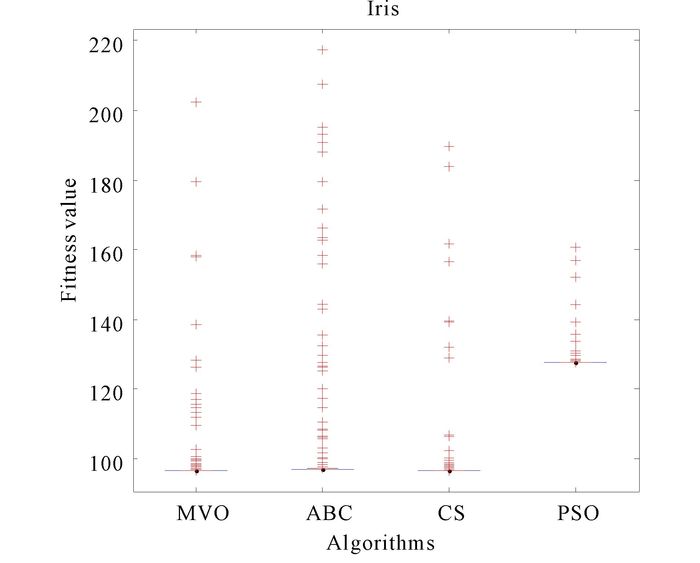
|
Fig.11 The anova test of algorithms for Iris |
Convergence curves of four algorithms for data set Iris are shown in Fig. 10.The curves in Fig. 10 show that MVO has a faster convergence speed than ABC and PSO.And the convergence curve of MVO is smoother than CS.Higher level of stability of MVO can be discovered in Fig. 11, which shows the anova test result for Iris.
3.2.4 Data set Contraceptive Method Choice (CMC)Contraceptive Method Choice (N=1 473, d=10, K=3):This data set is a subset of the 1987 National Indonesia Contraceptive Prevalence Survey.The samples are married women who were either not pregnant or do not know if they were at the time of interview.The problem is to predict the current contraceptive method choice (no use, long-term methods, or short-term methods) of a woman based on her demographic and socioeconomic characteristics.The clustering result of MVO for CMC is in Fig. 12.And the convergence curves of algorithms are shown in Fig. 13.In Fig. 14, it is the result of anova test for CMC.
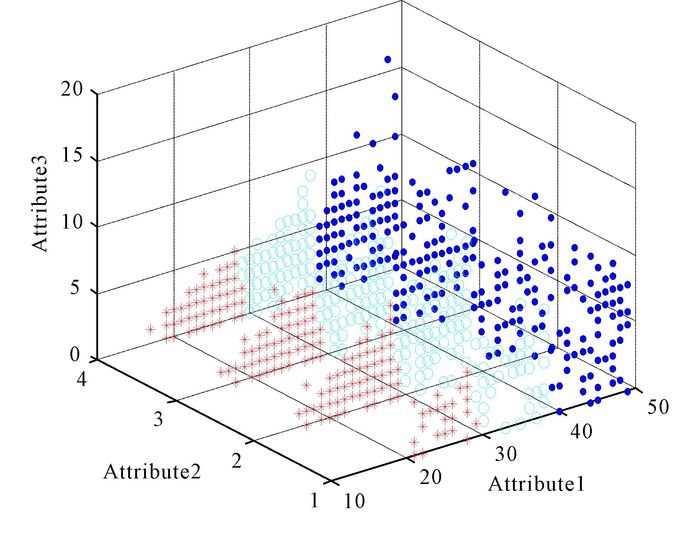
|
Fig.12 The clustering result of MVO for CMC |
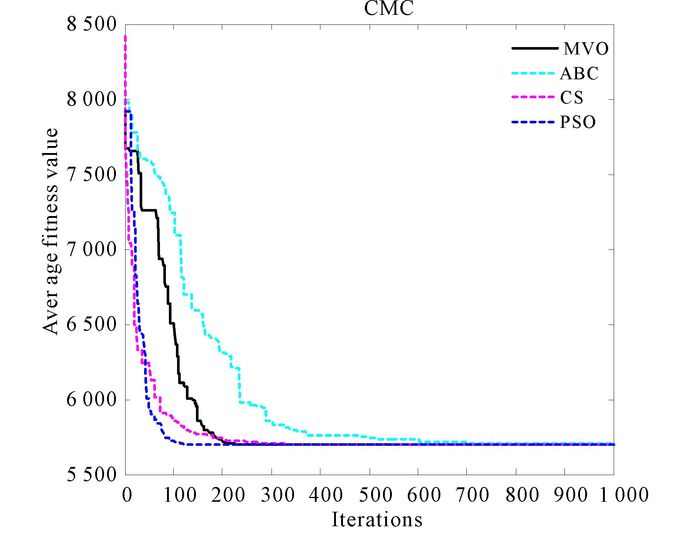
|
Fig.13 The convergence curves of algorithms for CMC |
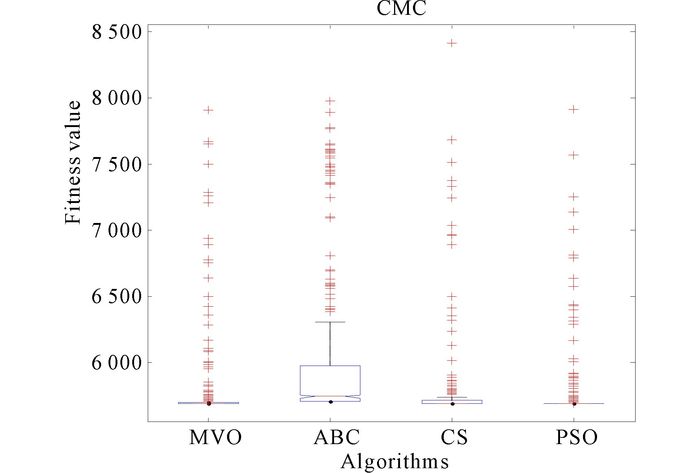
|
Fig.14 The anova test of algorithms for CMC |
And four convergence curves for data set CMC are shown in Fig. 13.The curve of PSO and CS is smoother than MVO.But faster convergence speed of MVO can be found as well.Fig. 14 shows that the stability of MVO and PSO are in high level.And the stability of MVO is better than ABC and CS.
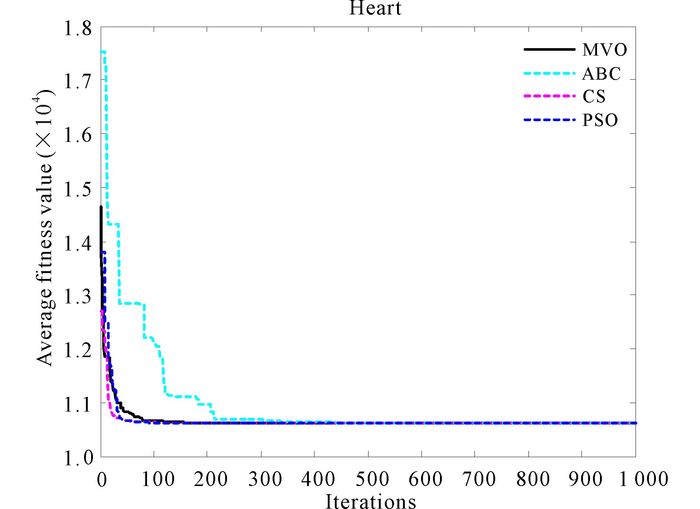
3.2.5 Data set Statlog (Heart)Statlog (Heart) data set (N=270, d=13, K=2):This data set is a heart disease database similar to a database already present in the repository (Heart Disease databases) but in a slightly different form.The clustering result of MVO for heart is in Fig. 15.And the convergence curves of algorithms are shown in Fig. 16.In Fig. 17, it is the result of anova test for Heart.

|
Fig.15 The clustering result of MVO for Heart |
|
Fig.16 The convergence curves of algorithms for Heart |

|
Fig.17 The anova test of algorithms for Heart |
Fig. 16shows that CS is faster than those of other algorithms for data set Heart.And MVO performs the second best.ABC shows the weakness of its ability to solving clustering problem for data set Heart.High level of stability of MVO can be discovered in Fig. 17, which shows the anova test result for Heart.
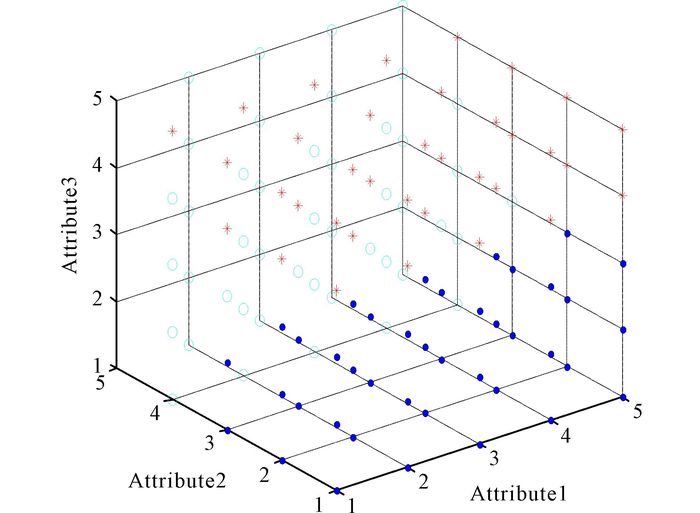
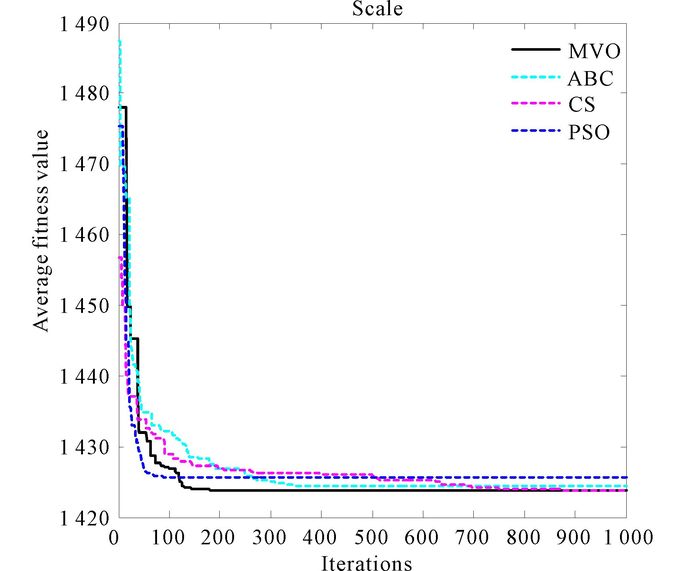
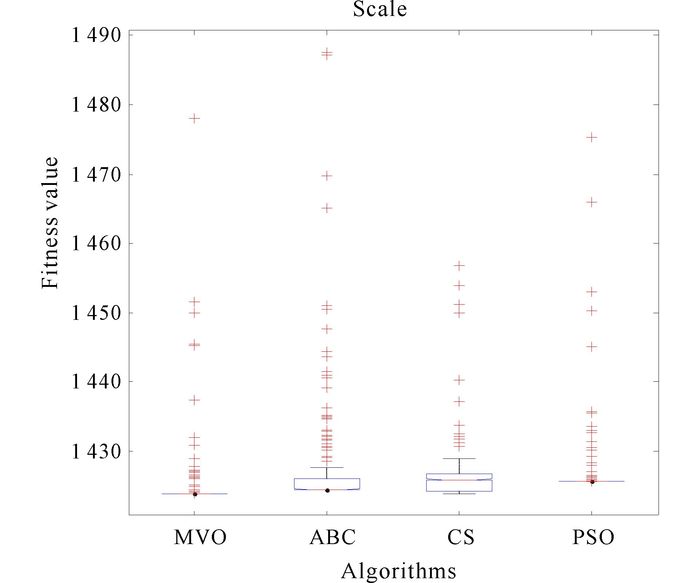
3.2.6 Data set Balance ScaleBalance Scale data (N=625, d=4, K=3):This data set is generated to model psychological experimental results.Each example is classified as having the balance scale tip to the right, tip to the left, or be balanced.The attributes are the left weight, the left distance, the right weight, and the right distance.The correct way to find the class is the greater of (left-distance*left-weight)and(right-distance*right-weight).If they are equal, it is balanced.The clustering result of MVO for Scale is in Fig. 18.And the convergence curves of algorithms are shown in Fig. 19.In Fig. 20, it is the result of anova test for Scale.
|
Fig.18 The clustering result of MVO for Scale |
|
Fig.19 The convergence curves of algorithms for Scale |
|
Fig.20 The anova test of algorithms for Scale |
Fig. 19 shows the convergence curves of mentioned population based algorithms.Faster convergence speed can be discovered easily from that MVO is the best.MVO is faster than PSO, ABC and CS.And in Fig. 20, the stability of MVO is also better than others.
3.2.7 Data set Haberman's SurvivalHaberman's Survival (N=306, d=3, K=2):The data set contains cases from a study that was conducted between 1958 and 1970 at the University of Chicago's Billings Hospital on the survival of patients who had undergone surgery for breast cancer.It records two survival status patients with age of patient at time of operation, patient's year of operation and number of positive axillary nodes detected.The clustering result of MVO for Survival in Fig. 21.And the convergence curves of algorithms are shown in Fig. 22.In Fig. 23, it is the result of anova test for Survival.
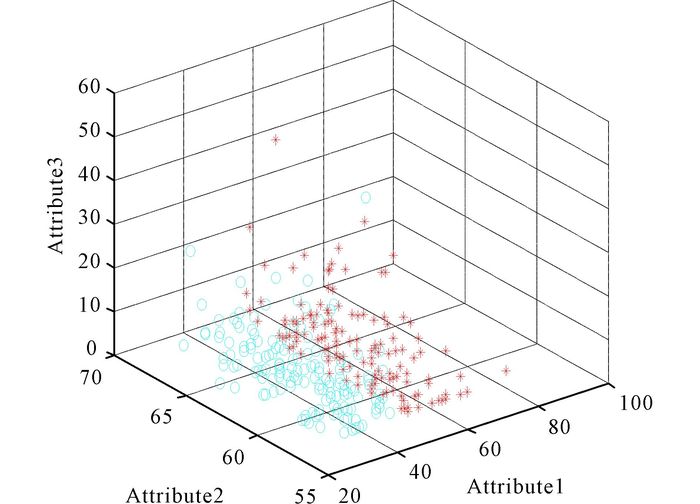
|
Fig.21 The clustering result of MVO for Survival |
|
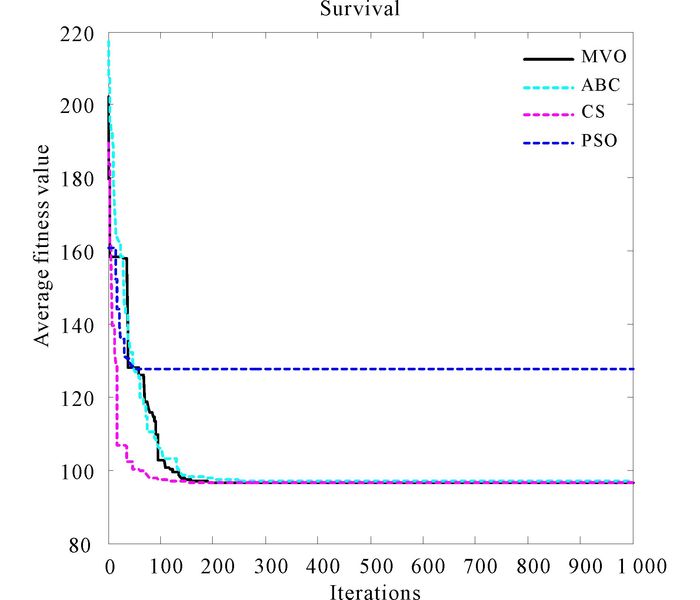
Fig.22 The convergence curves of algorithms for Survival |
|
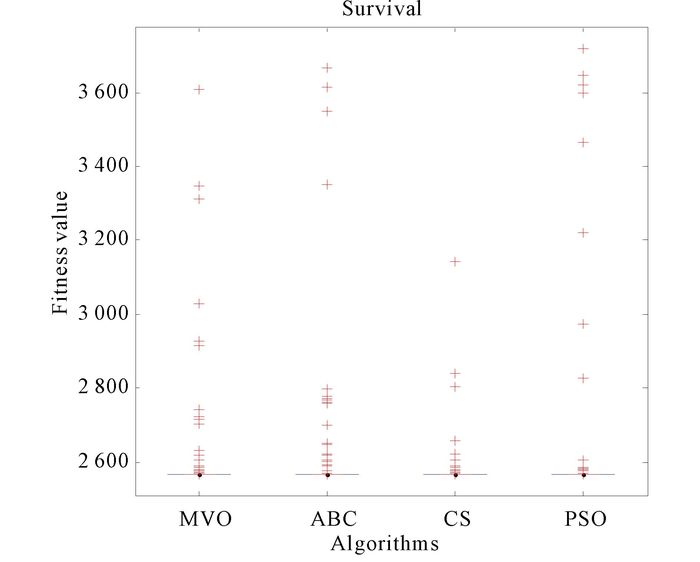
Fig.23 The anova test of algorithms for Survival |
Fig. 22 shows the convergence curves for data set Survival.From Fig. 22, MVO is the second best.And MVO is better than ABC and PSO.High degree stability of MVO can be found from Fig. 23 easily.
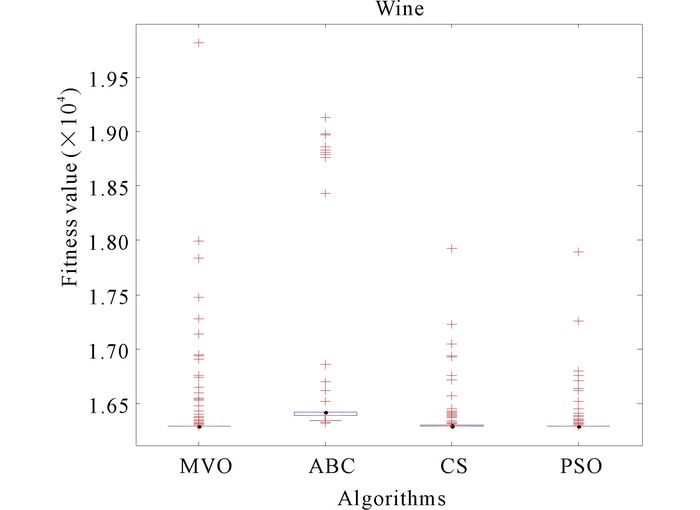
3.2.8 Data set WineWine data (N=178, d=13, K=3):This is the Wine data set, which is also taken from MCI laboratory.These data are the results of a chemical analysis of wines grown in the same region in Italy but derived from three different cultivars.The analysis determines the quantities of 13 constituents found in each of the three types of wines.There are 178 instances with 13 numeric attributes in Wine data set.All attributes are continuous.There is no missing attribute value.The clustering result of MVO for Wine is in Fig. 24.And the convergence curves of algorithms are shown in Fig. 25.In Fig. 26, it is the result of anova test for Wine.

|
Fig.24 The clustering result of MVO for Wine |
|
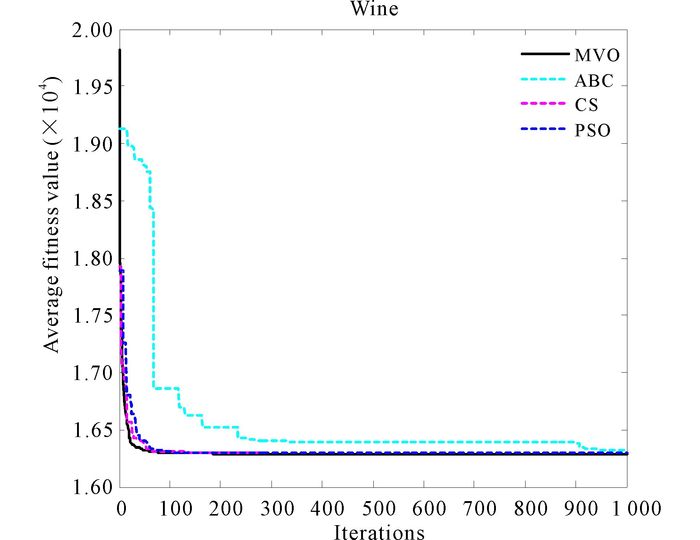
Fig.25 The convergence curves of algorithms for Wine |
|
Fig.26 The anova test of algorithms for Wine |
Convergence curves for data set Wine in Fig. 25 clearly show that MVO has a faster convergence speed.And its high degree of stability can be discovered in Fig. 26, which is the anova test for Wine.
Because the MVO algorithm has advantages such as simple structure, less parameters, easy to understand, excellent search ability.sufficient experiment has been carried out to eight the ability of proposed MVO for solving clustering problems.For validating eight comprehensively, eight data sets are used.Fig. 1-26 show the comparison of convergence curves, clustering result and the anova test results for different data sets.From these comparison figures, we can easily find that the convergence speed of MVO is faster than other algorithms mentioned in this paper in most cases.Another fact can be found that the stability of MVO can reach a relatively high level as well.
4 ConclusionsData clustering is a method for categorizing similar or dissimilar data.Nowadays, many researches are working in this field.Multi-verse optimization algorithm (MVO) for data clustering has been proposed in this paper.We experimented performance of our proposal on eight different data sets and compared the results with PSO, ABC, CS.For getting better performance, we ran 10 times with 1 000 iterations.The graphical experiment results show that Multi-verse optimization algorithm is more competitive than other algorithms for solving the clustering problem.The MVO is useful for solving data clustering problem.Future studies will extend the fitness function to explicitly optimize the intra-cluster distances.More elaborate tests on higher dimensional problems and large number of patterns will be done.
| [1] | SPIELMAN S E, THILL J C. Social area analysis, data mining, and GIS[J]. Computers Environment and Urban Systems, 2008, 32(2):110–122. DOI:10.1016/j.compenvurbsys.2007.11.004 |
| [2] | RAO M R. Cluster analysis and mathematical programming[J]. Journal of the American Statistical Association, 1971, 66(335):622–626. DOI:10.1080/01621459.1971.10482319 |
| [3] | HENDRICKS D, GEBBIE T, WILCOX D. High-speed detection of emergent market clustering via an unsupervised parallel genetic algorithm[J]. South African Journal of Science, 2016, 112(2):57–65. |
| [4] | TSAI C F, WU H C, TSAI C W. A new data clustering approach for data mining in large databases[C]//Proceedings of International Symposium on Parallel Architectures, Algorithms and Networks. Metro Manila: IEEE, 2002. |
| [5] | BLATT M, WISEMAN S, DOMANY E. Superparamagnetic clustering of data[J]. Physical Review Letters, 1996, 76(18):3251–3254. DOI:10.1103/PhysRevLett.76.3251 |
| [6] | FRIGUI H, KRISHNAPURAM R. A robust competitive clustering algorithm with applications in computer vision[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1999, 21(5):450–465. DOI:10.1109/34.765656 |
| [7] | ZAMANI K, MADADGAR S, BATENI S. Estimating soil thermal properties from land surface temperature measurements using ant colony optimization approach[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing. Toronto, Ont, Canada: IEEE, 1991: 873-876. |
| [8] | SHELOKAR P S, JAYARAMAN V K, KULKARNI B D. Ant algorithm for single and multiobjective reliability optimization problems[J]. Quality and Reliability Engineering International, 2002, 18(6):497–514. DOI:10.1002/(ISSN)1099-1638 |
| [9] | KENNEDY J, EBERHART R C. The particle swarm: Social adaptation in information-processing systems[M]//CORNE D, DORIGO M, GLOVER F (eds. ). New Ideas in Optimization. Maidenhead, UK: McGraw-Hill Ltd, 1999: 379-388. |
| [10] | MIRJALILI S, MIRJALILI S M, HATAMLOU A. Multi-verse optimizer:A nature-inspired algorithm for global optimization[J]. Neural Computing and Applications, 2016, 27(2):495–513. DOI:10.1007/s00521-015-1870-7 |
| [11] | MORRIS M S, THORNE K S. Wormholes in spacetime and their use for interstellar travel:A tool for teaching general relativity[J]. American Journal of Physics, 1988, 56(5):395–412. DOI:10.1119/1.15620 |
| [12] | GUTH A H. Eternal inflation and its implications[J]. Journal of Physics A:Mathematical and Theoretical, 2007, 40(25):6811–6826. DOI:10.1088/1751-8113/40/25/S25 |
| [13] | HAWKING S W. Black hole explosions?[J]. Nature, 1974, 248(5443):30–31. DOI:10.1038/248030a0 |
| [14] | HALLIDAY D, RESNICK R, WALKER J. Fundamentals of physics extended[M]. 8th edition. New York: Wiley, 2008. |
| [15] | SCHUTZ B. Book review:Gravity from the ground up[M]. New York: Cambridge University Press, 2004: 22. |
| [16] | ZHAO M R, TANG H L, GUO J, et al. A data clustering algorithm using cuckoo search[M]//HUNG J, YEN N, LI K C (eds. ). Frontier Computing. Singapore: Springer, 2016. |
| [17] | BOUYER A. An optimized k-harmonic means algorithm combined with modified particle swarm optimization and cuckoo search algorithm[J]. Foundations of Computing and Decision Sciences, 2016, 41(2):99–121. DOI:10.1515/fcds-2016-0006 |
| [18] | SENTHILNATH J, DAS V, OMKAR S N, et al. Clustering using levy flight cuckoo search[C]//Proceedings of Seventh International Conference on Bio-Inspired Computing: Theories and Applications. India: Springer, 2013, 202: 65-75. |
| [19] | ELKERAN A. A new approach for sheet nesting problem using guided cuckoo search and pairwise clustering[J]. European Journal of Operational Research, 2013, 231(3):757–769. DOI:10.1016/j.ejor.2013.06.020 |
| [20] | BENAMEUR L, ALAMI J, IMRANI A H E. A new hybrid particle swarm optimization algorithm for handling multiobjective problem using fuzzy clustering technique[C]//Proceedings of the 2009 International Conference on Computational Intelligence, Modelling and Simulation. Washington DC, USA: IEEE Computer Society, 2009: 48-53. |
| [21] | SHI Y L, NAN J Z. Fuzzy c-means and fuzzy adaptive particle swarm optimization for clustering problem[J]. Journal of Computational and Theoretical Nanoscience, 2016, 13(1):270–273. DOI:10.1166/jctn.2016.4800 |
| [22] | SUN L L, CHEN H N. Artificial bee colony algorithm based on clustering method and its application for optimal power flow problem[M]//GONG M, PAN L, SONG T, et al(eds. ). Bio-inspired Computing-Theories and Applications. Singapore: Springer, 2016. |
| [23] | KARABOGA D, OKDEM S, OZTURK C. Cluster based wireless sensor network routing using artificial bee colony algorithm[J]. Wireless Networks, 2012, 18(7):847–860. DOI:10.1007/s11276-012-0438-z |
| [24] | ZHANG Y D, WU L N, WANG S H, et al. Chaotic artificial bee colony used for cluster analysis[M]//CHEN R (ed. ). Intelligent Computing and Information Science. Berlin Heidelberg: Springer, 2011: 205-211. |
 2017, Vol. 24
2017, Vol. 24 



