【研究意义】粒子群优化算法PSO (Particle Swarm Optimization,简称PSO)最早是由Kennedy和Eberhart[1]于1995年提出的一种启发式全局优化技术。在粒子群优化算法中,每个优化问题的解都被看做是搜索空间中没有体积和质量的微粒,并延伸到N维空间中去,其中每个粒子的位置和飞行速度都表示为N维空间中的一个矢量。与其它优化算法相比,PSO对优化目标函数的模型没有特殊要求、可调整的参数少、算法收敛速度快, 并且具有随机性和扩充性,自提出以来就受到许多学者的关注,并已成功应用到许多领域中,如多目标优化[2]、模糊系统控制[3]和神经网络训练[4]等。【前人研究进展】为提高粒子群优化算法的性能,很多学者对PSO算法进行不同方面的改进。如胡旺等[5]通过增加极值扰动算子来帮助粒子有效摆脱局部极值点;刘伟等[6]提出一个惯性权重函数,使算法的全局搜索能力与局部搜索能力得到良好平衡,加快收敛速度;Wang等[7]通过在最佳粒子处进行柯西变异,以引导其它粒子向更好位置靠拢。【本研究切入点】将扰动因子加入速度更新公式中,采用自适应的惯性权重,并对优粒子进行自适应的柯西变异,以克服标准粒子群优化算法在迭代后期收敛速度慢、搜索精度不高、容易陷入局部最优等的缺点。【拟解决的关键问题】与其它粒子群改进方法相比较,得出每种改进方法的优缺点,为进一步研究粒子群优化算法的改进和应用提供科学依据。
1 标准粒子群优化算法(SPSO)在粒子群优化算法中,每个粒子都有一个速度vi,其可以决定粒子的飞行轨迹,粒子位置的优劣用一个适应度函数来确定。其中,粒子的飞行轨迹是根据其学习自身经验pbest和群体中的最好经验gbest来确定的。自身经验pbest是指,粒子知道本身当前位置和目前为止它发现的最好位置pbest;群体中的最好经验gbest是指,群体中目前为止发现的最好位置gbest。
Kennedy和Eberhart[1]最早提出的PSO算法的速度与位置更新公式如下:
| $\begin{align} & {{v}_{i}}t+1={{v}_{i}}\left( t \right)+{{c}_{1}}{{r}_{1}}\left( pbes{{t}_{i}}\left( t \right)-{{x}_{i}}\left( t \right) \right)+ \\ & {{c}_{2}}{{r}_{2}}\left( gbest\left( t \right)-{{x}_{i}}\left( t \right) \right), \\ \end{align}$ | (1) |
| ${{x}_{i}}\left( t+1 \right)={{x}_{i}}\left( t \right)+{{v}_{i}}\left( t+1 \right),$ | (2) |
其中:t为当前迭代次数,c1和c2为学习因子,r1、r2是分布在[0, 1]内的随机数,pbest为个体极值,gbest为全局极值。
为提高PSO算法的收敛性能,考虑到对不同的问题,局部和全局的优能力权衡不一样,Shi和Eberhart[8]在1998年引入惯性权重ω,将其添加到基本粒子群算法的速度更新公式中,即
| $\begin{align} & {{v}_{i}}\left( t+1 \right)=\omega \left( t \right){{v}_{i}}\left( t \right)+{{c}_{1}}{{r}_{1}}(pbes{{t}_{i}}\left( t \right)- \\ & {{x}_{i}}\left( t \right))+{{c}_{2}}{{r}_{2}}(gbest\left( t \right)-{{x}_{i}}(t)), \\ \end{align}$ | (3) |
| $\omega ={{\omega }_{\text{max }\!\!~\!\!\text{ }}}-\left( {{\omega }_{\text{max }\!\!~\!\!\text{ }}}-{{\omega }_{\text{max }\!\!~\!\!\text{ }}} \right)*t/{{T}_{\text{max }\!\!~\!\!\text{ }}}。$ | (4) |
其中ωmax、ωmin分别是最大和最小惯性权重,t、Tmax分别为粒子当前迭代次数和最大迭代次数。
2 粒子群优化算法的改进在PSO中,粒子随个体极值pbest和全局极值gbest在解空间中移动,如果粒子的个体极值pbest一直处于优势,算法就容易陷入局部最优;当粒子陷入局部极值时,算法就会过早收敛,这样会使粒子停滞在局部区域,出现“早熟”现象,只能求得局部最优解。为使粒子避免“早熟”现象,本研究从以下3个方面对标准粒子群优化算法进行改进。
2.1 极值扰动的引入粒子种群都有趋同性,即当基本粒子群优化算法处于进化停滞时,粒子速度vi难以及时更新,粒子会出现“聚集”现象,这时粒子只能在一个较小的范围内搜索,容易使算法陷入局部最优。想要求得问题的全局最优解,必须克服粒子群优化算法易陷入局部最优的缺陷,其中,扩大搜索范围是有效的措施之一。因此,本研究在速度更新公式中引入扰动因子r3和r4,对个体极值pbest和全局极值gbest进行随机调整,从而扩大粒子的搜索范围,帮助粒子跳出局部最优。受胡旺等[5]研究的启发,本研究将速度更新公式更改如下:
| $\begin{align} & {{v}_{i}}\left( t+1 \right)=\omega \left( t \right){{v}_{i}}\left( t \right)+{{c}_{1}}{{r}_{1}}\left( {{r}_{3}}~2\text{ }pbes{{t}_{i}} \right.\left( t \right)- \\ & {{x}_{i}}\left. \left( t \right) \right)+{{c}_{2}}{{r}_{2}}\left( {{r}_{4}}~2\text{ }gbest \right.\left( t \right)-{{x}_{i}}\left. \left( t \right) \right), \\ \end{align}$ | (5) |
其中r3和r4是[0, 1]间均匀分布的随机数,个体极值pbest和全局极值gbest会在r3、r4的扰动下随机调整,使粒子在更大的空间范围内进行搜索,这样粒子找到最优解的概率就会增大,从而有可能跳出局部最优解。
2.2 自适应惯性权重在粒子群优化算法中,惯性权重ω是一个很重要的可调整参数,设置合理的惯性权重值,可以平衡PSO算法的全局与局部寻优能力。较大的ω会使算法的全局寻优能力提高,而较小的ω会使算法的局部寻优能力增强。对于ω来说,线性递减的惯性权重只对某些问题有效,当待解决问题很复杂时,该法会使得PSO算法容易在进化末期陷入局部最优,无法找到要求的最优解。根据刘伟等[6]的报道,本研究提出以下惯性权重改进公式:
| $\omega ={{\omega }_{\text{min }\!\!~\!\!\text{ }}}+\text{exp}~{{\left( -50*t/{{T}_{\text{max }\!\!~\!\!\text{ }}} \right)}^{2}}*({{\omega }_{\text{max }\!\!~\!\!\text{ }}}-{{\omega }_{\text{max }\!\!~\!\!\text{ }}})。$ | (6) |
由上述公式可知,此惯性权重函数为一个非线性的、呈指数形式递减的函数,它会使ω在迭代初期能长时间保持一个较大的值,从而增加迭代初期的全局搜索时间和全局搜索强度;而在迭代后期能长时间保持一个较小的值,从而增加迭代后期的局部搜索时间和局部搜索强度,加快收敛速度。
2.3 自适应柯西变异PSO算法在收敛之前,最优解gbest的选取会在之前的几个候选粒子之间振荡。因此,对最优粒子gbest进行变异操作,可以扩展粒子的搜索空间,帮助粒子突破障碍逃离局部最优。在Wang等[7]研究的基础上,本研究提出一种自适应的柯西变异策略,即对每次迭代中的gbest进行变异操作,避免粒子过早收敛。
柯西分布是一个连续型的分布函数,它的数学期望(即期望和方差)均不存在。标准柯西分布函数如下:
| $F\left( x \right)=\frac{1}{2}+\frac{1}{\pi }\text{arctan}~\left( x \right)。$ | (7) |
在本研究提出的自适应柯西变异策略中,首先分别计算N个个体的pbest在各维上的平均值avg_pbest(i):
| $avg\_pbest\left( i \right)=\left( \sum\limits_{j=1}^{N}{pbest}\text{ }[j]\ [i]\text{ } \right)/N,$ | (8) |
式(8) 中,i=1, 2, …D,pbest[j][i]是第j个粒子在第i维上的位置。应用下式(9) 计算avg_pbest(i)到gbest上每一维的距离,ri越小,群体间越相似,将获得距原gbest位越远的变异位。
| $r\left( i \right)=gbest\left( i \right)-avg\_pbest\left( i \right)。$ | (9) |
将r(i)代入到式(10) 中:
| $xm\left( i \right)=\text{exp}~\left( -\rho \cdot t/{{T}_{\text{max }\!\!~\!\!\text{ }}} \right)\cdot \left( 1-r\left( i \right)/{{r}_{\text{max }\!\!~\!\!\text{ }}} \right),$ | (10) |
式(10) 中,ρ是常数,本研究中取ρ=20;rmax是各维间最大距离。将式(10) 代入到式(7) 中。
自适应柯西变异操作如式(11) 所示:
| $gbest\prime \left( i \right)=gbest\left( i \right)+z\left( i \right)\cdot F\left( xm \right),$ | (11) |
| $z\left( i \right)=\left( \sum\limits_{j=1}^{N}{v}\left[ j \right]\ \left[ i \right] \right)/N,$ | (12) |
z(i)是各维变异权重平均值,v[j][i]为第j个粒子在第i维上的速度分量。
2.4 基于扰动的自适应粒子群优化算法综合2.1~2.3,本研究提出一种基于扰动的自适应粒子群优化算法(Adaptive PSO based on disturbances),简称ADPSO,该算法的步骤如下。
步骤1:随机初始化粒子的位置xi与速度vi;
步骤2:设置第i个粒子的当前位置为pbest,最优粒子的位置为gbest;
步骤3:粒子状态调整,按公式(2)、(5)、(6) 对粒子的速度和位置进行更新;
步骤4:根据适应度函数f(x)计算粒子i的适应度f(xi);
步骤5:比较f(xi)与f(pbest),若f(xi)优于f(pbest),就将该粒子的pbest更新为xi;
步骤6:比较f(xi)与f(gbest),若f(xi)优于f(gbest),就将gbest更新为xi;
步骤7:对当前获得的gbest用自适应柯西变异策略即式(11) 进行变异操作;
步骤8:判断算法是否达到最大迭代次数,若是,转步骤9,否则转步骤3;
步骤9:输出gbest和相应的目标函数值f(gbest),算法结束。
3 仿真实验将本研究提出的基于扰动的自适应粒子群优化算法(ADPSO)与以下3个算法相比较:① 标准粒子群优化算法(SPSO),② 自适应变异的粒子群算法(AMPSO) [9],③ 带收缩与发散操作的自适应粒子群优化算法(seAPSO) [10]。分别用5个基准测试函数f1:Sphere、f2:Rosenbrock、f3:Ackley、f4:Griewank、f5:Rastrigin(理论最小值均为0) 来进行优化性能测试。
| $\begin{align} & {{f}_{1}}\left( x \right)=\sum\limits_{i=1}^{D}{x_{i}^{2}}, \\ & {{f}_{2}}\left( x \right)=\sum\limits_{i=1}^{D-1}{\left[ {{\left( 1-{{x}_{i}} \right)}^{2}}+100{{\left( {{x}_{i+1}}-x_{i}^{2} \right)}^{2}} \right]}, \\ & {{f}_{3}}\left( x \right)=-\quad 20\quad \text{exp}\left( -\quad 0.2\quad \sqrt{\frac{1}{D}\sum\limits_{i=1}^{D}{x_{i}^{2}}}~ \right)- \\ & \text{exp}\left( \text{ }\frac{1}{D}\sum\limits_{i=1}^{D}{\text{cos}}2\pi {{x}_{i}} \right)+20+e, \\ & {{f}_{4}}\left( x \right)=\frac{1}{4000}\sum\limits_{i=1}^{D}{x_{i}^{2}}-\prod\limits_{i=1}^{D}{\left( \text{cos}~\frac{{{x}_{i}}}{\sqrt{i}} \right)}+1, \\ & {{f}_{5}}\left( x \right)=\sum\limits_{i=1}^{D}{\left[ x_{i}^{2}-10\text{cos}\left( 2\pi {{x}_{i}} \right)+10 \right]}B \\ \end{align}$ |
对本实验中的参数进行如下设置:粒子群的种群规模N=40,粒子维数D=30,最大迭代次数Tmax=500,c1=c2=1.496 2,ωmax=0.95,ωmin=0.4,AMPSO和seAPSO算法的参数按原文献的设置。针对每个函数运行20次求平均值,分别将SPSO、AMPSO、seAPSO、ADPSO记为A1、A2、A3、A4,仿真结果与统计数据见表 1,每个函数的适应度进化曲线如图 1~5所示。
| 表 1 测试结果 Table 1 Experimental results |
|
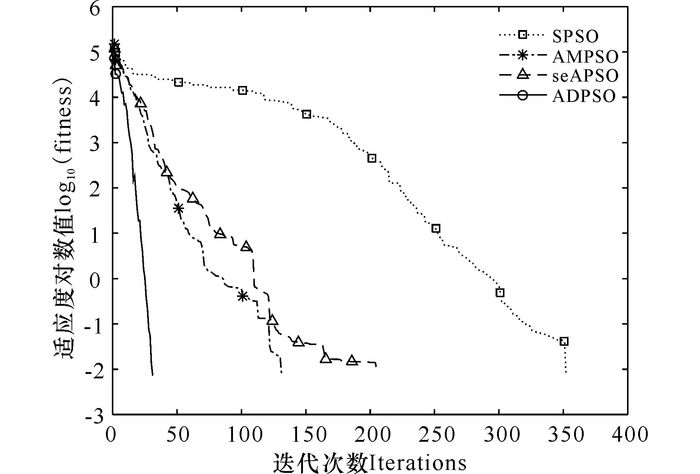
图 1 函数Sphere(f1)寻优进化曲线 Fig.1 Optimization curve for Sphere (f1) |
|
图 2 函数Rosenbrock(f2)寻优进化曲线 Fig.2 Optimization curve for Rosenbrock (f2) |
|
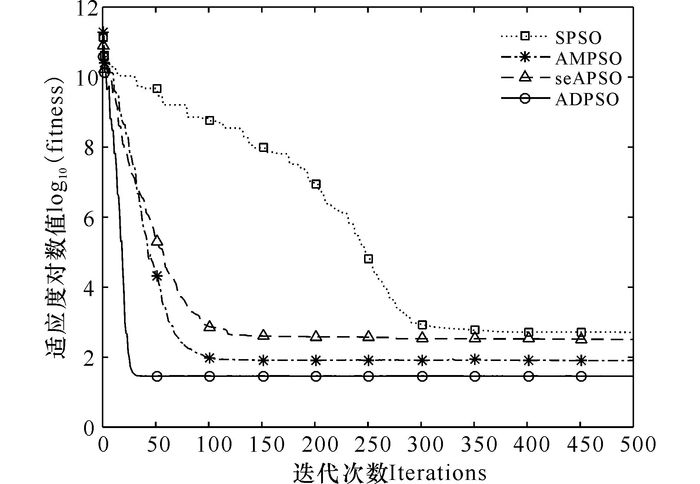
图 3 函数Ackley(f3)寻优进化曲线 Fig.3 Optimization curve for Ackley (f3) |
|
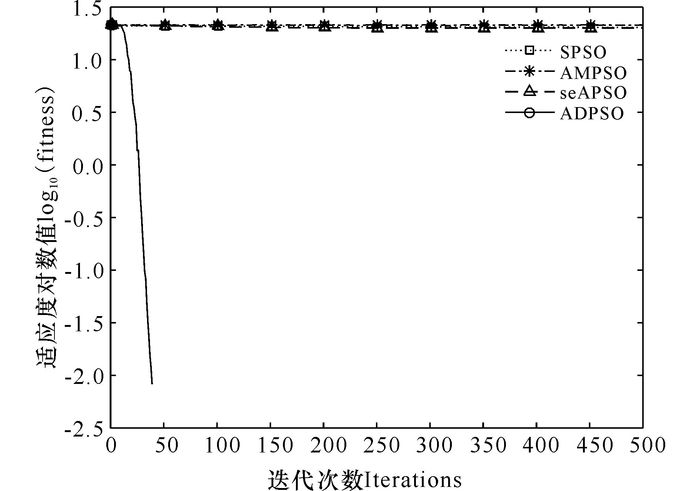
图 4 函数Griewank (f4)寻优进化曲线 Fig.4 Optimization curve for Griewank (f4) |
|
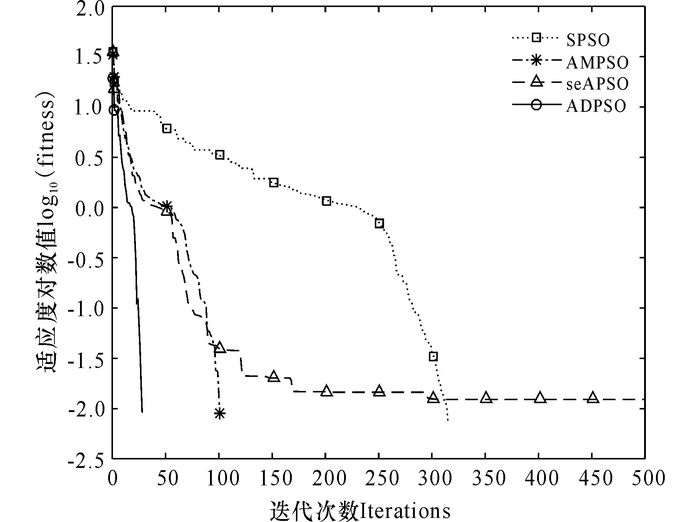
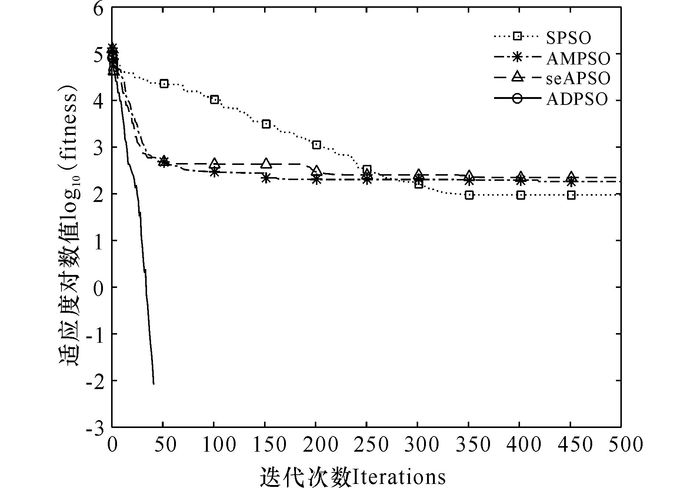
图 5 函数Rastrigin (f5)寻优进化曲线 Fig.5 Optimization curve for Rastrigin (f5) |
函数f1主要用于算法寻优精度的测试,是一个非线性的对称单峰函数,ADPSO算法相比于其它3个算法具有更快的收敛速度,优化性能更好(图 1)。函数f2是一个很难极小化的典型病态二次函数,ADPSO相对其它算法收敛速度更快,获得的平均最优解也更好(图 2)。函数f3、f4、f5均是具有大量局部极小值的多峰函数,普通算法很容易陷入局部最优从而停止进化,无法取得最优解或近似最优解。从图 3可以看出,SPSO、AMPSO和seAPSO算法都陷入局部最优,而ADPSO算法由于在迭代初期就突破障碍逃离局部最优点,在进化末期才能取得近似全局最优解。如图 4所示,AMPSO算法和ADPSO算法都能够最后收敛于接近理论最优解的全局最优解,具有良好的收敛效果,但ADPSO算法具有更快的收敛速度。从图 5可以发现,只有ADPSO算法在进化前期突破了障碍,并且算法的收敛速度和收敛精度都比其它3个算法要好很多。
通过以上分析可知,本研究提出的ADPSO算法较其它3种算法具有更高的收敛精度和收敛速度,是一种更加有效和快速的粒子群优化算法。
4 结论本研究在标准PSO算法的基础上进行改进,提出基于扰动的自适应粒子群优化算法(ADPSO)。该算法在速度更新公式中增加扰动因子,采用自适应的惯性权重,并对最优粒子进行自适应的柯西变异。通过实验仿真与对比分析,提出的新算法增强了全局搜索能力,具有更高的优化性能,使粒子群的收敛精度和速度得到明显提高。
| [1] |
KENNEDY J, EBERHART R.Particle swarm optimization[C]//IEEE International Conference on Neural Networks.Perth:IEEE, 1995:1942-1948.
|
| [2] |
徐鹤鸣. 多目标粒子群优化算法的研究[D]. 上海: 上海交通大学, 2013. XU H M.Research on multiobjective particle swarm optimization algorithms[D].Shanghai:Shanghai Jiao Tong University, 2013. |
| [3] |
孟庆宽, 仇瑞承, 张漫, 等. 基于改进粒子群优化模糊控制的农业车辆导航系统[J]. 农业机械学报, 2015, 46(3): 29-36, 58. MENG Q K, QIU R C, ZHANG M, et al. Navigation system of agricultural vehicle based on fuzzy logic controller with improved particle swarm optimization algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(3): 29-36, 58. DOI:10.6041/j.issn.1000-1298.2015.03.005 |
| [4] |
高海兵, 高亮, 周驰, 等. 基于粒子群优化的神经网络训练算法研究[J]. 电子学报, 2004, 32(9): 1572-1574. GAO H B, GAO L, ZHOU C, et al. Particle swarm optimization based algorithm for neural network learning[J]. Acta Electronica Sinica, 2004, 32(9): 1572-1574. |
| [5] |
胡旺, 李志蜀. 一种更简化而高效的粒子群优化算法[J]. 软件学报, 2007, 18(4): 861-868. HU W, LI Z S. A simpler and more effective particle swarm optimization algorithm[J]. Journal of Software, 2007, 18(4): 861-868. |
| [6] |
刘伟, 周育人. 一种改进惯性权重的PSO算法[J]. 计算机工程与应用, 2009, 45(7): 46-48, 55. LIU W, ZHOU Y R. Modifed inertia weight particle swarm optimizer[J]. Computer Engineering and Applications, 2009, 45(7): 46-48, 55. |
| [7] |
WANG H, LI C H, LIU Y, et al.A hybrid particle swarm algorithm with Cauchy mutation[C]//IEEE Swarm Intelligence Symposium.Honolulu:IEEE, 2007:356-360. https://link.springer.com/chapter/10.1007/978-981-10-0356-1_12
|
| [8] |
SHI Y, EBERHART C.A modified particle swarm optimizer[C]//IEEE International Conference on Evolutionary Computation.Anchorage, Alaska:IEEE, 1998.
|
| [9] |
吕振肃, 侯志荣. 自适应变异的粒子群优化算法[J]. 电子学报, 2004, 32(3): 416-420. LV Z S, HOU Z R. Particle swarm optimization with adaptive mutation[J]. Acta Electronica Sinica, 2004, 32(3): 416-420. |
| [10] |
赵志刚, 尹兆远, 林玉娇. 带收缩与发散操作的自适应粒子群优化算法[J]. 计算机科学, 2015, 42(S1): 48-51. ZHAO Z G, YIN Z Y, LIN Y J. Adaptive particle swarm optimization algorithm with shrink and expansion operation[J]. Computer Science, 2015, 42(S1): 48-51. |
 2017, Vol. 24
2017, Vol. 24 

