2. 广西大学计算机与电子信息学院, 广西 南宁 530004
2. School of Computer, Electronics and Information in Guangxi University, Nanning, Guangxi, 530004, China
Texture synthesis from samples (TSFS) has developed rapidly in recent years.The basic thought of TSFS is giving a small piece of sample image to generate large and continuous texture similar to the sample[1].TSFS is divided into two-dimensional texture synthesis from samples (2D-TSFS) and three-dimensional texture synthesis from samples (3D-TSFS).Most of the 2D-TSFS methods regarded generation of texture as a Markov process[2-3].These methods worked well but the speeds were very slow.They were improved by the algorithms of the vector coding on texture[4] and the pyramid synthesis[5].The 3D-TSFS methods synthesized the texture over the three-dimensional (3D) geometric surface from samples directly[6-10].Based on a given texture sample, the methods generated texture over the entire surface in accordance with the geometric configuration of the surface.The results were visually similar and continuous.
By far, a number of 3D-TSFS techniques have been put forward and most of them were built on grid models.In the texture synthesis algorithms, these traditional techniques used topology information contained in surfaces.There were few researches about synthesizing texture directly on the 3D point set surface.
Recently, point based representations have been proposed as an alternative to triangles for 3D surfaces, with a number of advantages.No 'mesh', or connectivity information has to be stored explicitly.This allows a simple and compact representation, ideal for fast rendering and editing.
The original sampling points obtained from the scanner surface are called geometric information.The grid topology information is actually from the original geometric information via complicated processing such as generating triangular patches on point model and so on.In this article, we will synthesize texture directly on 3D point set surfaces without reconstructing grid model from the surfaces which is illustrated in figure 1.
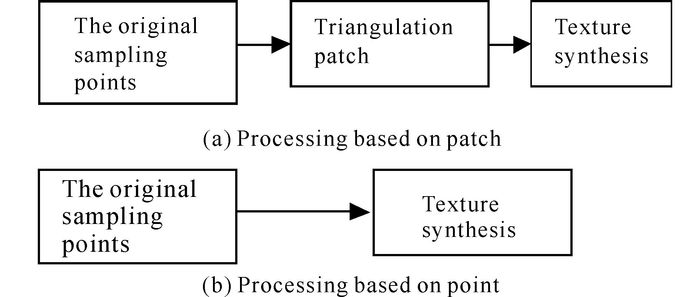
|
Fig.1 Comparison of the two processing procedure |
A large number of algorithms of texture synthesis from samples have been proposed.Heeger and Bergen[11] synthesized texture using the Laplace and controllable Pyramid.Debonet used a similar approach.Efos and Leung brought forward a more direct algorithm.Firstly they set a few seeds in the surface to be synthesized and then found the matching points in the sample via the given neighborhood, and finally randomly selected a match point to complete the rendering[12].Wei and Levoy[4] proposed a similar algorithm and greatly accelerated the process of synthesis by means of vector quantization.Efros[8] brought out a texture synthesis algorithm based on block collage.In the meantime, Wei[10] used a multi-scale algorithm to synthesize surface texture.Turk[13] used a similar approach.Zhang[14] proposed the gradient texture method which obtained gradient texture effect on the surface.BTF' synthesis method generated a wealth of micro-structure on the surface[15].While most of these methods were based on triangle mesh, there were few of them could achieve the synthesis closing to interactive rate[8].The methods of texture synthesis could be extended to the processing of the other things.For example, we could generate voice[16], sport[14] and video[17-18] via texture synthesis.Moreover, the techniques of texture synthesis could be used to repair image and video.
Abandoning triangulation methods, the image processing technologies on point-based surfaces only record the information of points, from which the final image can be reconstructed.The technologies provide new avenues for solving fast image processing of a large number of three-dimensional sampled points data.In the last few years, a large number of papers related to point-based surfaces have emerged.We briefly outline those related to our work.Clarenz and Rumpf[19] researched how to do the geometry processing of finite elements on point based surfaces and proposed a pixel-based algorithm to synthesize surface texture as an example.Xiao and Zhao[20] presented a novel technique for texture synthesis on point-sampled geometry using global optimization.By adding special extra terms to the energy function, the authors implemented a user controllable texture synthesis algorithm for point set surfaces on 3D flow fields.The experimental results have greatly increased.
2 The Process of Texture SynthesisWe propose a high speed and effective algorithm to synthesize the texture over 3D point set surface abandoning triangulation.The flow chart of texture synthesis on 3D point set surface is illustrated in figure 2 and the basic steps can be summarized as follows.

|
Fig.2 Flow chart of texture synthesis on 3D point set surface |
We select an initial point or more on 3D point set surface in the first step and load the data of sample pattern to obtain texture data of pixels point in the sample.
The points distributing on the 3D point model are discrete, so we need to establish the relationship among the points to prepare for the texture synthesis.In our algorithm, we establish neighborhood relations of the points via KD-tree, so each of the points on the 3D surface has a set of adjacent points as its neighborhood points.The size of the neighborhood can be adjusted by the parameters of KD-tree, so we can acquire suitable neighborhood relations.
2.2 Initializing texture valuesInitialization is indispensable in the process of the texture synthesis.The initial texture value on the 3D surface is acquired via initializing the texture of the initial point which we obtain in the first step, and it is regarded as the based texture for texture synthesis.But it is not enough if we only synthesize the initial point.To solve this problem we put the neighborhood points of the initial point into the ranks of initialization, and their texture values are also regarded as the based texture.Initializing texture is divided into three steps:
1) Assign the initial point i a texture value from the sample image randomly.
2) Calculate the texture values of the neighborhood points of i.
a) Projecting the direction between i and all surrounding points ik onto i's tangent plane and retaining the distance information.
Projecting:
Direction[ik]=points[ik].pos-points[i].pos
Direction[ik]=Direction[ik]-Dot(Direction[ik], normal[i])*normal[i]
Normalizing:
Direction[ik]=Normalize(Direction[ik])
Calculating the distance between ik and i:
d = Euclid_diance(ik, i)
Retaining the distance information:
Direction[ik]=d*Direction[ik]
b) The direction of i is recorded as d and the normal vector of i is recorded as n.We create a new coordinate system on i's tangent plane.The point i is the origin of coordinate.The direction d is Y-axis.The direction n×d is X-axis(n×d is derived from the vector cross product formula of solid geometry).
Regarding the average distance h between points and points on 3D model as a unit, we calculate the step length Δx, Δy on X-axis and Y-axis for each projection vector obtained in the previous step.
c) In the sample image, regarding the point which a texture value has be assigned to the initial point as the center and pixel as the unit, we find the point whose distance to the center is Δx, Δy units respectively on X-axis and Y-axis and assign the texture value of the point to the neighborhood point corresponding with the point projection vector.For each neighborhood point, the operation is repeated.
3) Initialize the border set
All of the points on 3D model are divided into three sets of points Y, B, N.The points having texture value belong to the set Y.The points without a texture value and near to the points of Y belong to the set B—The border set.The other points belong to the set N.
Attach a label to the points with initialized texture value and put them into set Y.The distances between each point in the set Y and the initial point i are calculated and saved to the variable geodesic_distance[ik].
Attach a label to the neighborhood points ikn of the points in the set Y and without a texture value, and put them to the border set B.The distances between each point in the set B and the initial point i are calculated via the following formula:
geodesic_distance[ikn]=min{ geodesic_distance[ikn],
geodesic_distance[ik]+Euclid_diance(ik, ikn)}.
2.3 Establishing orientation field over 3D surfaceWe must specify directions on 3D point set surface before texture synthesis, because sample texture has directivity.The directions of a few points can be specified by the user and the directions of the absolutely major points have to acquire directions via algorithm.The algorithm used the method similar to Dijkstra's.The geodesic distances between the user-specified point and the other points were calculated.The new direction was calculated as the sum of the directions of all adjacent points having directions, weighted using the Gaussians.The direction of each point was acquired from the near to the distance.So the orientation field over the surface was established.
2.4 Selecting the next pointSelecting the next point to be rendered is the first step in the core of texture synthesis.We need to select the point matching the condition as the next point.If we select the next point from all of the points on the point based model, the speed of texture synthesis will be very slow.To solve this problem we use the border set B.
Selecting the next point from the border set B can greatly narrow the scope of the operation and improve the efficiency of texture synthesis.Every point in the set Y and B contains information about the distance to the closest point with a texture value.The point with the smallest distance from B is selected as the next point p.
2.5 Establishing the mapping between the next point and the sample imageIn order to calculate the texture value of the point p and finish rendering, the mapping between the point p and the sample is established, and then the best matching texture value in the sample is found out.
The process to establish mapping between the point p and the sample is as follows:
1) Projecting the direction between p and all surrounding points onto p's tangent plane and retaining the distance information (Similar to our method used in section Ⅲ.2.1).
2) Creating a new coordinate system and establishing a regular matching grid in the coordinate system.
The direction of p is recorded as d and the normal vector of p is recorded as n.We create a new coordinate system on p's tangent plane.The point p is the origin of coordinate.The direction d is Y-axis.The direction n×d is X-axis (Similar to our method used in section Ⅲ.3.1).
With the point p as the center, we build a N×N grid G of N×N points tij with a distance of h in the new coordinate system.The numerical value h is the average distance between points and points on the 3D model.In this article we establish the mapping between the points on the 3D model and the pixels in the sample via the grid G.
3) Assigning the texture value to the points tij
For each point tij on the grid G, we select the closest projected point pij.On the 3D point set surface we find out the point mij corresponding to pij.If the point mij belongs to the set Y, we assign the color of mij to tij and tij is marked as assigned.Else, tij is marked as unassigned.
2.6 Finding the value of texture and assignmentIn the sample, with each of the points as the center and pixel as the unit, we build N×N grids from which we find out the grid C with minimum color difference via comparing all grids to the grid G as illustrating in figure 3.The color of the center point q of grid C is the texture value of the point p.
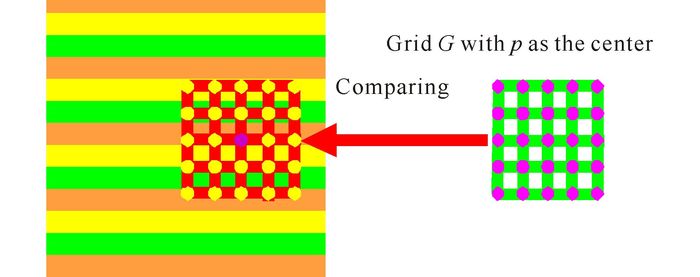
|
Fig.3 Searching the matching point in the sample |
In this article, we propose a new assignment method.As well as following the traditional pattern of single-point assignment, we carry out a new algorithm for multi-point synchronous assignment via the neighborhood and mapping relations.The new assignment method is divided into two steps:
1) Single-point assignment for the point p
We assign the color of the center point q of grid C to the point p.The point p is marked as assigned and included in the set Y.We attach a label to the p's neighborhood points without the texture value, and put them to the border set B.
2) Multi-point synchronous assignment
We find out the points tij of the grid G that have not the texture value and the points mij of the 3D model corresponding with them.We assign the color of the corresponding points of grid C to the points mij and finish assignment.The points mij are marked as assigned and included in the set Y.We attach a label to the mij 's neighborhood points without the texture value, and put them to the border set B.
2.7 Assignment and renderingWe repeat the processing in section Ⅲ.2.4~2.6 until each point on the 3D point set model has a texture value and is rendered.
3 ResultsWe carry out our algorithm on the computer with processor 1 600 MHz and core storage 256 MB.We synthesize texture on 3D bunny model with 35 283 sampling points.On the model, the average distance h between points and points is 0.012 528.In the experiment, we obtain different results via changing parameters.The results are presented in table 1 and figure 4.
| Table 1 The experiment data of texture synthesis on 3D point set surface |

|
Fig.4 Results of texture |
We have presented a fast-speed and effective algorithm to synthesize texture over 3D point set surface abandoning triangulation.We finish texture synthesis via seven steps.The experimental results show that the method can produce smooth texture synthesis as well as keeping the structures in the sample texture and the speed of processing is fast.In the future, we will further enhance the effect and the speed of texture synthesis on piont set surface.Moreover, we will reseach texture synthesis on piont set surface from Multi-sample images.
| [1] | VINOD KUMAR R S, ARIVAZHAGAN S. Adaptive patch based texture synthesis using contourlet transform[J]. Journal of Intelligent & Fuzzy Systems:Applications in Engineering and Technology Archive, 2015, 28(3):1061–1070. |
| [2] | DESPINE G, COLLEU T. Adaptive texture synthesis for large scale city modeling[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2015, 5(4):155–162. |
| [3] | NAJM A, LABROSSE F. Image completion by structure reconstruction and texture synthesis[J]. Pattern Analysis and Applications, 2015, 18(2):333–350. DOI:10.1007/s10044-013-0348-4 |
| [4] | MARIAM Z, ALAA N E. Texture synthesis by reaction diffusion process[J]. Annals of the University of Craiova, 2015, 42(1):56–69. |
| [5] | PARRA A, ORTIZ J M. Adapting a texture synthesis algorithm for conditional multiple point geostatistical simulation[J]. Stochastic Environmental Research and Risk Assessment, 2011, 25(8):1101–1111. DOI:10.1007/s00477-011-0489-1 |
| [6] | ZHAO Y, QIAN W H, CHEN Q, et al. Optimization methods to texture synthesis[J]. Advanced Materials Research, 2011, 217-218:662–667. DOI:10.4028/www.scientific.net/AMR.217-218 |
| [7] | HUANG S B, ZHU X L, XU Y Y, et al. An improved image inpainting algorithm based on texture synthesis[J]. Journal of Hefei University of Technology:Natural Science, 2011, 34(2):313–316, 320. |
| [8] | EFROS A A, FREEMAN W T. Image quilting for texture synthesis and transfer[C]//Proceedings of SIGGRAPH 2001. Los Angeles, USA: ACM, 2001: 341-346. |
| [9] | WU Q, YU Y Z. Feature matching and deformation for texture synthesis[C]//Proceedings of SIGGRAPH 2004. Los Angeles, USA: ACM, 2004: 364-367. |
| [10] | WEI L Y, LEVOY M. Fast texture synthesis using tree-structured vector quantization[C]//Proceedings of SIGGRAPH 2000. New Orleans, Louisiana, USA: ACM, 2000: 479-488. |
| [11] | LIANG L, LIU C, XU Y Q, et al. Real-time texture synthesis by patch based sampling[J]. ACM Transactions on Graphics, 2001, 20(3):127–150. DOI:10.1145/501786.501787 |
| [12] | WU F L, MEI C H, SHI J Y. Method of direct texture synthesis on arbitrary surfaces[J]. Journal of Computer Science and Technology, 2004, 19(5):643–649. DOI:10.1007/BF02945590 |
| [13] | TURK G. Texture synthesis on surfaces[C]//Proceedings of SIGGRAPH'2001. Los Angeles, CA, USA: ACM, 2001: 347-354. |
| [14] | ZHANG J D, ZHOU K, VELHO L, et al. Synthesis of progressively-variant textures on arbitrary surfaces[C]//Proceedings of ACM SIGGRAPH 2003. New York: ACM, 2003: 295-302. |
| [15] | MAGDA S, KRIEGMAN D. Fast texture synthesis on arbitrary meshes[C]//Proceedings of the 14th Eurographics Workshop on Rendering. Switzerland: Eurographics Association, 2003: 82-89. |
| [16] | EFROS A A, LEUNG T K. Texture synthesis by non-parametric sampling[C]//ICCV'99 Proceedings of the International Conference on Computer Vision. Washington, DC: IEEE, 1999: 1033-1038. |
| [17] | TONG X, ZHANG J D, LIU L G, et al. Synthesis of bidirectional texture functions on arbitrary surfaces[C]//Proceedings of the 29th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM, 2002: 665-672. |
| [18] | BHAT K S, SEITZ S M, HODGINS J K, et al. Flow-based video synthesis and editing[C]//Proceedings of Siggraph'2004. Los Angeles, USA: ACM, 2004: 360-370. |
| [19] | CLARENZ U, RUMPF M, TELEA A. Finite elements on point based surfaces[C]//Proceedings of the First Eurographics Conference on Point-Based. Switzerland: Eurographics Association, 2004. |
| [20] | XIAO C X, ZHAO Y, ZHENG W T, et al. Texture synthesis for point-sampled geometry based on global optimization[J]. Chinese Journal of Computers, 2006, 12(29):2061–2070. |
 2017, Vol. 24
2017, Vol. 24 

