2. 广西壮族自治区环境监测中心站, 广西南宁 530028;
3. 澳大利亚昆士兰大学地球与环境科学学院, 布里斯班 4072
2. Guangxi Environmental Monitoring Centre, Nanning, Guangxi, 530028, China;
3. School of Earth and Environmental Science, University of Queensland, Brisbane, 4072, Australia
【研究意义】目前,地表水的年度监测数据统计中,采用年均值评价是一种常态。因刁江流域受上游污染水质波动较大,均值计算过程中会将高浓度的超标值屏蔽,常常出现虽有单值超标但年均值远远优于执行标准的情况,反映不出水质的真实情况,容易给管理者一种假象而导致管理疏漏。因此,本文拟研究一种科学、客观的水质大数据的综合评价方法,为刁江流域重金属污染治理提供客观数据。【前人研究进展】国外对河流的水环境质量评价研究始于20世纪60年代,以Jacobs[1]提出水质指数 (Index of water quality,WQI) 概念的水体质量评价方法为标志,许多西方学者采用不同方法对水环境质量评价进行了研究。当前我国环保部门主要采用均值法、单因子评价法和综合污染指数法来评价河流水质,这些方法面对大数据的分析评价局限性日益凸显,水质波动较大时评价结果不尽如人意[2-5]。随着环境统计学的发展,模糊数学法[6]、贝叶斯法[7-9]、多元统计法[10-11]、灰色评价法[12]、神经网络法[13]等也被尝试应用到水质评价中。但因河流水文条件复杂,不确定性因素多,不同的水质评价方法有各自的优点和不足,如贝叶斯法及多元统计法在选择和数据统计方面考虑得较为完善,但未考虑评价过程中的不确定因素;模糊数学法虽然考虑了不确定性但却缺乏决策性[14];神经网络则适用于大数据的分析,但因技术问题难以用于日常评价。【本研究切入点】评价方法存在的缺陷一直是水环境管理的瓶颈之一,本研究是在三角模糊数广泛应用于水质、沉积物及土壤评价的基础上[15-16],利用区间数学α-截集技术原理对其进行处理后再将其运用到贝叶斯模型中,目的在于充分考虑水质的不确定因素,又让评价结果具有决断性,目前利用该方法评价刁江水质未有报道。【拟解决的关键问题】采用基于α-截集的三角模糊数-贝叶斯模型,兼具考虑模型结构和水质参数的不确定性,对刁江2015年度主要特征污染物铅、镉、砷的监测结果进行统计分析,以期获得更加准确的水质评价结果,为刁江污染治理提供依据。
1 材料与方法 1.1 监测断面及因子刁江流域地处桂西北,地理位置为东经107°30′~108°30′,北纬24°42′~25°37′,北界接邻南丹县城,东邻金城江市,南界至金钗,西到都安县。刁江是广西河池市的一条重要河流,珠江水系红水河的一级支流,发源于南丹县南关镇拉所村,由北向南流经南丹县、金城江区和都安瑶族自治县,在都安百旺乡那浩村汇入红水河,全程229 km[17]。
本研究分别在刁江的上、中、下游共选取5个代表断面,其中:上游选金洞村断面 (A) 及岜腊屯断面 (B),中游选五花陇村断面 (C) 及那浪桥断面 (D),下游选马陇断面 (E),监测断面分布图及监测断面见图 1。
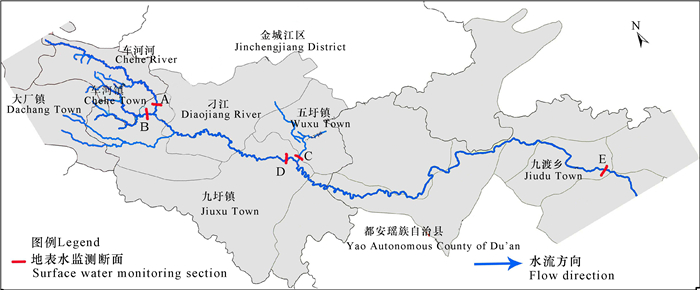
|
图 1 刁江流域分布及监测断面 Fig.1 Diaojiang River basin distribution and monitoring section |
刁江地表水例行监测一共监测25个因子,多年的监测数据表明,除铅、镉、砷超标外,其余因子常年稳定达标,因此本研究选取2015年5个断面的铅、镉、砷3个因子开展研究。
1.2 采样与分析位于下游的马陇断面水质稳定且长期达标,每月采样1次;其余4个断面,受污染源影响的可能性较大,需要更多的研究数据,每月采样2次。采样依据《地表水和污水监测技术规范》(HJ/T 91—2002),水样采集后沉淀30 min,砷取上清液装瓶,铅、镉经0.45 μm滤膜过滤后装瓶,现场分别加入浓硝酸致pH值小于2,并同步采集全程序空白样品及不少于样品总数10%的平行样。
样品分析依据相关的方法标准开展,采用电感耦合等离子质谱仪Agilent7700E ICP-MS进行上机分析测定。为了保证仪器的稳定和准确,在每次测定过程中均插入标样,标样测定值在真值的95%置信区间内,样品加标回收率为95%~105%,平行样测定值的相对偏差保持在10%以内,全程序空白测定结果未检出,所有质控结果满足要求。
1.3 评价方法在水质评价中,设实数a,b,c分别为水质评价指标浓度的最小可能值、最可能值和最大可能值,且a≤b≤c,则 (a,b,c) 构成三角模糊数
| $ {{\tilde \theta }_\alpha } = [\tilde \theta _\alpha ^L,\tilde \theta _\alpha ^R\left] = \right[\left( {b - a} \right)\alpha + a, - \left( {c - b} \right)\alpha + c], $ | (1) |
设i为水质类别 (Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类、Ⅴ类),j为监测指标,k为监测点位,则三角模糊化的贝叶斯水质评价模型可表示为[12]
| $ {{\tilde P}^\alpha }({y_{ij}}|\tilde x_{kj}^\alpha ) = \frac{{P({y_{ij}}){{\tilde P}^\alpha }(\tilde x_{kj}^\alpha |{y_{ij}})}}{{\sum _{i = 1}^sP({y_{ij}}){{\tilde P}^\alpha }(\tilde x_{kj}^\alpha |{y_{ij}})}}, $ | (2) |
式中,yij表示当水质类别为i时,第j个水质指标的标准限值;
| $ {{\tilde P}^\alpha }(\tilde x_{kj}^\alpha |{y_{ij}}) = \frac{{1/\tilde D_{ij}^\alpha }}{{\sum _{i = 1}^s1/\tilde D_{ij}^\alpha }}, $ | (3) |
式中,
在得出各监测指标对应各水质类别的后验概率后,根据水质分级标准矩阵计算监测指标的权重[18],结合变异系数法,各水质指标权重的水质综合后验概率计算公示如下:
| $ \tilde P_i^\alpha = \sum _{j = 1}^n{w_j}{{\tilde P}^\alpha }({y_{ij}}|\tilde x_{kj}^\alpha ), $ | (4) |
| $ {w_j} = {\delta _j}/\sum _{j = 1}^n{\delta _j}, $ | (5) |
| $ {\delta _j} = \sqrt {\frac{{\sum _{i = 1}^5{{({y_{ij}} - {{\bar y}_j})}^2}}}{5}} /{{\bar y}_j}, $ | (6) |
式中,n为水质评价指标的个数;
利用模糊化原理,采用专家咨询法对各水质类别赋值,描述水质优劣状况,并计算水质综合得分
| $ {{\tilde M}^\alpha } = \sum _{i = 1}^5\tilde P_i^\alpha \times {M_i}, $ | (7) |
评价标准的等值及分值见表 1;若跨越两个区间,则可计算
| $ \rho \left( i \right) = \frac{{\left| {\left[ {a,b} \right] \cap \left[ {{a_i},{b_i}} \right]} \right|}}{{\left| {\left[ {a,b} \right]} \right|}}, $ | (8) |
| 表 1 评价标准区间及分值 Table 1 Levels and values of the assessment standards |
式中,ρ(i) 表示[a, b]对[ai, bi]的隶属度,[ai, bi]表示第i个水质类别;∩表示交集,||表示区间的几何长度。
2 结果与分析 2.1 三角模糊数的α-截集处理将刁江2015年1—12月份5个监测断面的铅、镉、砷的监测数据转化为三角模糊数,并用α-截集来简化。即将三角模糊数转化为可信度水平下对应的区间数
| 表 2 α-截集处理后的刁江水质监测结果 Table 2 Monitoring data of Diaojiang River treated by α-cut |
有研究认为:若无任何水质信息,先验分布可选择均匀分布进行贝叶斯推理;而在有水质信息的情况下水质监测数据服从正态分布[19],可选择正态分布作为先验分布。因此,本研究以2012年—2014年间刁江5个监测断面的监测数据为先验信息,选择正态分布为先验分布,计算出各监测指标对各水质类别的先验概率,具体见表 3。
| 表 3 各水质类别的先验概率 Table 3 The Prior probabilities of water quality |
由《地表水环境质量标准》(GB 3838—2002) 可以得到铅、镉、砷各类别 (Ⅰ类、Ⅱ类、Ⅲ类、Ⅳ类、Ⅴ类) 水质标准矩阵为[20]:
| $ S = \left| {\begin{array}{*{20}{c}} {0.01}&{0.01}&{0.05}&{0.05}&{0.1}\\ {0.001}&{0.005}&{0.005}&{0.005}&{0.01}\\ {0.05}&{0.05}&{0.05}&{0.1}&{0.1} \end{array}} \right|。$ |
根据水质分级标准矩阵,运用变异系数法由式 (5)、式 (6) 求得铅、镉、砷的权重分别为0.456 4,0.332 0,0.211 5,由式 (3) 求得铅、镉、砷对应各水质类别的的条件概率,代入式 (2) 求各指标对应的水质类别的后验概率,再代入式 (4) 即可得出2015年综合考虑了各评价指标权重的水质后验概率,具体见表 4。
| 表 4 各类别水质的后验概率 Table 4 The posterior probabilities of water quality |
根据式 (7) 得出2015年各监测点水质综合得分的区间值并最终确定水质类别,根据式 (8) 求得跨越两个区间的水质隶属度;同时,依据传统贝叶斯模型、三角模糊数模型及均值模型求得2015年的水质类别, 具体见表 5。
| 表 5 2015年刁江各监测断面水质的综合评价结果 Table 5 Comprehensive water quality assessment results of Diaojiang River in 2015 |
本研究模型的评价结果表明,2015年刁江A (金洞村断面)、D (那浪桥断面) 断面水质达到Ⅱ类水标准,E (马陇断面) 断面水质达Ⅰ类水标准,B (岜腊屯断面)、C (花陇村断面) 断面水质介于Ⅱ、Ⅲ类水之间,对各级的隶属度分别为 (
将本研究模型的评价结果与传统贝叶斯模型、三角模糊数模型及年均值模型的评价结果进行了比较 (表 5),4种模型的评价结果中:A、E两个断面的评价结果一致,原因是这两个断面的水质较为稳定,A断面其上游的污染源较为稳定,E断面则远离污染源,因此两个断面年中水质波动不大,4种评价模型的都适用;B、C两个断面的评价结果差异最大,因B、C所处位置为刁江流域重金属污染源的集中区,分布着许多年代久远已经废弃的采矿隆口及尾矿库,受自然条件、天气变化等不确定因素影响,水质波动频繁,致使监测数据的相对标准偏差增大,因此三角模糊数模型较其它模型得出的水质结果会差些,而均值模型则会平均了差异性。综合比较,传统贝叶斯模型与本研究模型的评价结果接近,三角模糊数模型次之,均值模型在水质不稳定时相差较大。
相比之下,基于α-截集的三角模糊数-贝叶斯模型,既继承其它3个模型的优点,又弥补了它们的不足之处:
1) 三角模糊数模型虽然能反映指标浓度在一定置信度水平下的不确定性,但因其仅是将浓度表示成三角模糊数的形式,直接与水质标准做简单比较,强调极值的模型结构过于简单。
2) 传统贝叶斯模型的模型参数采用均值输入,求得各水质类别的可能性,与各水质类别标准都进行相应的比较,若以最大后验概率所在的水质类别来评价,虽具有决策性,但评价结果无法考虑其它水质类别的可能性。
3) 均值模型将一年中1—12月份的浓度进行加和平均,在水质稳定的情况下,均值模型最优,但在水质波动的情况下,因突发事故的高浓度值会被正常状态下的低浓度值拉平,容易造成水质良好的假象,这就是本次对比中部分断面其评价结果与其它模型差异较大的原因所在。
4) 本研究的基于α-截集的三角模糊数-贝叶斯模型的评价结果是以隶属度的方式表达了水质的不确定性,考虑了各种污染因子的权重,引用历史数据作为先验分布来计算先验概率,且各水质类别的后验概率都参与综合得分的运算,为水质评价中的不确定性提供了新的思路,能够客观、科学、全面地评价刁江的水质状况,可为刁江的治理提供科学的决策依据。
3 结论基于α-截集的三角模糊数-贝叶斯模型对刁江5个断面的特征污染物进行评价研究,结果表明,2015年刁江A、D断面水质达到Ⅱ类水标准,E断面水质达Ⅰ类水标准,B、C断面水质介于Ⅱ、Ⅲ类水之间,对各级的隶属度分别为 (
基于α-截集的三角模糊数-贝叶斯模型继承了三角模糊数模型的不确定性,弥补了其模型结构上的不足;继承了传统贝叶斯模型的决策性,弥补了其在不确定性问题上的不足;继承了均值模型评价稳定水质的优越性,弥补了其在水质波动情况下的不足。因此,本研究模型兼具水质评价模型中的决策性及不确定性等优点,具有一定的优越性。
| [1] |
JACOBS H L. Water quality criteria[J]. Journal of Water Pollution Control Federation, 1965, 37(5): 292-300. |
| [2] |
张亚丽, 周扬, 程真, 等. 不同水质评价方法在丹江口流域水质评价中应用比较[J]. 中国环境监测, 2015, 31(3): 58-61. ZHANG Y L, ZHOU Y, CHENG Z, et al. Comparison and analysis of different evaluation methods for water quality in the Danjiangkou valley[J]. Environmental Monitoring in China, 2015, 31(3): 58-61. |
| [3] |
崔雪梅, 赵盼盼, 章爱群. 4种河流水质评价方法的比较研究--以槐荫河为例[J]. 节水灌溉, 2015(5): 46-48, 51. CUI X M, ZHAO P P, ZHANG A Q. Comparative analysis of four methods for water quality assessment-a case study of Huaiyin river[J]. Water Saving Irrigation, 2015(5): 46-48, 51. |
| [4] |
徐蕾. 综合指数评价法在地表水饮用水源地水质评价中的应用[J]. 农业与技术, 2013, 33(4): 36-37. XU L. Application of comprehensive index evaluation method in water quality assessment of surface water sources[J]. Agriculture and Technology, 2013, 33(4): 36-37. |
| [5] |
刘琰, 郑丙辉, 付青, 等. 水污染指数法在河流水质评价中的应用研究[J]. 中国环境监测, 2013, 29(3): 49-55. LIU Y, ZHENG B H, FU Q, et al. Application of water pollution index in water quality assessment of rivers[J]. Environmental Monitoring in China, 2013, 29(3): 49-55. |
| [6] |
焦士兴, 王腊春, 杨顺喜, 等. 基于三角模糊函数的城市饮用水水源地安全评价--以河南省安阳市为例[J]. 自然资源学报, 2012, 27(7): 1112-1123. JIAO S X, WANG L C, YANG S X, et al. Security assessment of urban drinking water sources based on triangular fuzzy numbers-a case study of Anyang City, Henan Province[J]. Journal of Natural Resources, 2012, 27(7): 1112-1123. DOI:10.11849/zrzyxb.2012.07.004 |
| [7] |
孙鹏程, 陈吉宁. 基于贝叶斯网络的河流突发性水质污染事故风险评估[J]. 环境科学, 2009, 30(1): 47-51. SUN P C, CHEN J N. Risk assessment of river water quality under accidental pollution based on Bayesian networks[J]. Environmental Sciences, 2009, 30(1): 47-51. |
| [8] |
毛志, 陈亚丽. 基于贝叶斯公式的河流水质综合评价--以铜仁市锦江河为例[J]. 铜仁学院学报, 2016, 18(4): 150-153. MAO Z, CHEN Y L. The comprehensive assessment of water quality based on Bayesian Formula-taking Jinjiang River as an example[J]. Journal of Tongren University, 2016, 18(4): 150-153. |
| [9] |
廖杰, 王文圣, 丁晶. 贝叶斯公式在河流水质综合评价中的应用[J]. 四川师范大学学报:自然科学版, 2007, 30(4): 519-522. LIAO J, WANG W S, DING J. Comprehensive assessment of water quality on main rivers in Sichuan by bayes method[J]. Journal of Sichuan Normal University:Natural Science Edition, 2007, 30(4): 519-522. |
| [10] |
富天乙, 邹志红, 王晓静. 基于多元统计和水质标识指数的辽阳太子河水质评价研究[J]. 环境科学学报, 2014, 34(2): 473-480. FU T Y, ZOU Z H, WANG X J. Water quality assessment for Taizi River watershed in Liaoyang section based on multivariate statistical analysis and water quality identification index[J]. Acta Scientiae Circumstantiae, 2014, 34(2): 473-480. |
| [11] |
ZHANG Y, GUO F, MENG W, et al. Water quality assessment and source identification of Daliao river basin using multivariate statistical methods[J]. Environmental Monitoring and Assessment, 2009, 152: 105-121. DOI:10.1007/s10661-008-0300-z |
| [12] |
张小君, 徐中民, 宋晓谕, 等. 几种水环境质量评价方法在青海湖入湖河流中的应用[J]. 环境工程, 2013, 31(1): 117-121. ZHANG X J, XU Z M, SONG X Y, et al. Application and study of several water quality evaluation method in rivers flowing into Qinghai Lake[J]. Environment Engineering, 2013, 31(1): 117-121. DOI:10.11835/j.issn.1005-2909.2013.01.027 |
| [13] |
张升东, 徐征和, 杜敏, 等. 基于BP神经网络的卧虎山水库水质评价[J]. 济南大学学报:自然科学版, 2013, 27(4): 419-423. ZHANG S D, XU Z H, DU M, et al. Assessment on water quality based on BP ANN model for Wohushan reservoir[J]. Journal of University of Jinan:Science and Technology, 2013, 27(4): 419-423. |
| [14] |
余勋, 梁婕, 曾光明, 等. 基于三角模糊数的贝叶斯水质评价模型[J]. 环境科学学报, 2013, 33(3): 904-909. YU X, LIANG J, ZENG G M, et al. An integrated fuzzy-bayesian water quality assessment model based on triangular fuzzy numbers[J]. Acta Scientiae Circumstantiae, 2013, 33(3): 904-909. |
| [15] |
樊梦佳, 袁兴中, 祝慧娜, 等. 基于三角模糊数的河流沉积物中重金属污染评价模型[J]. 环境科学学报, 2010, 30(8): 1700-1706. FAN M J, YUAN X Z, ZHU H N, et al. Assessment model for heavy metal pollution in river sediment based on triangular fuzzy numbers[J]. Acta Scientiae Circumstantiae, 2010, 30(8): 1700-1706. |
| [16] |
李飞, 黄瑾辉, 曾光明, 等. 基于三角模糊数和重金属化学形态的土壤重金属污染综合评价模型[J]. 环境科学学报, 2012, 32(2): 432-439. LI F, HUANG J H, ZENG G M, et al. An integrated assessment model for heavy metal pollution in soil based on triangular fuzzy numbers and chemical speciation of heavy metal[J]. Acta Scientiae Circumstantiae, 2012, 32(2): 432-439. |
| [17] |
蹇丽. 广西刁江水系重金属及形态砷的空间分异与形成机制研究[D]. 咸阳: 西北农林科技大学, 2010. JIAN L.Research on spatial distribution and formation mecharism of heavy metals and arsenic species in Guangxi Diaojiang river[D].Xianyang:Northwest Agriculture and Forestry University, 2010. |
| [18] |
屈卫军. 基于变异系数法的灰色关联决策模型在节水工程方案优选中的应用[J]. 地下水, 2010, 32(5): 50-51. QU W J. Application of gray correlative decision-making model for optimization of water-saving project scheme based on the variation coefficient method[J]. Groundwater, 2010, 32(5): 50-51. |
| [19] |
GLEIT A. Estimation for small normal data sets with detection limits[J]. Environmental Science & Technology, 1985, 19(12): 1201-1206. |
| [20] |
国家环境保护总局, 国家质量监督检验检疫总局. 地表水环境质量标准: GB 3838-2002[S]. 北京: 中国环境科学出版社, 2002. The State Environmental Protection Administration, State Administration of Quality Supervision, Inspection and Quarantine.Environmental quality standards for surface water:GB 3838-2002[S].Beijing:China Environmental Science Press, 2002. |
 2017, Vol. 24
2017, Vol. 24 


