【研究意义】水体漫衰减系数(Kd)是描述辐照度随海水深度增加而衰减的重要海洋光学参数之一[1]。它与水体下行辐照度密切相关。清澈水体中,悬浮物、叶绿素等物质含量较少,水体下行辐照度随海水深度增加而衰减的趋势小且呈现出稳定的状态,因此漫衰减系数较小且基本保持不变;浑浊水体中含有较多的悬浮物、泥沙等,下行辐照度衰减程度较大,因此漫衰减系数整体较大。当水体出现分层的情况,且上层水体浑浊度小于下层水体浑浊度时,下行辐照度随深度增加的衰减程度会在一定深度处增大,因此漫衰减系数会在一定深度处增大;而当上层水体浑浊度大于下层水体时,则下行辐照度随深度增加的衰减程度会到一定深度处减小,因此漫衰减系数会在到达一定深度后减小。研究漫衰减系数具有重要意义:1)有助于反映水体环境状况,计算水体透明度;2)漫衰减系数可以反映光在水体中的分布变化特征。因此,反演水体的漫衰减系数不仅有利于研究大面积水域的水体组分变化和光学特性,还有利于宏观、动态地监测水体。【前人研究进展】目前已有许多学者对漫衰减系数反演开展了研究。Austin等[2-3]首次利用统计回归的方法建立了Kd(490)和蓝、绿两波段的离水辐亮度的统计关系;Mueller[4]基于SeaWiFS卫星利用490 nm与555 nm波段的标准离水辐亮度来反演Kd(490);王晓梅等[5]针对黄东海区域,利用555 nm与665 nm波段的遥感反射率以及490 nm与555 nm的遥感反射比,即(Rrs(555)+Rrs(665))以及(Rrs(490)/Rrs(555))来反演Kd(490);张亭禄等[6]采用COASTLOOC与NOMAD数据集建立了漫衰减系数的经验反演算法,结果表明经验算法虽然简单直接,但欠缺理论依据,当反演的区域或时间不同时容易造成误差。现有的漫衰减系数的经验反演算法研究大多在开阔、清澈的水域即一类水体反演效果良好,但对于沿岸、内陆等区域的浑浊水体处,即二类水体,反演效果相对较差;Lee等[7-8]首次提出利用水下的遥感反射比反演吸收系数和后向散射系数的算法,进而建立漫衰减系数与吸收系数与后向散射散射系数之间的关系;Doron等[9]在此基础上利用490 nm与709 nm波段的辐照度和反射率反演得到bb(490),再进一步得到a(490),并最终反演出Kd(490);吴婷婷等[10]在Doran算法的基础上加入了光场分布系数。【本研究切入点】经验算法在清澈水域中的反演精度和稳定度效果较好,但在浑浊水域处反演效果并不理想。而半分析算法在浑浊水域反演效果优于经验算法,但在清澈水域处劣于经验算法。就我国渤黄海水体而言,水体成分复杂,水体类型多样,且辐照度衰减的影响因子不尽相同,可以建立一个适合于我国渤黄海水域精度高且稳定的漫衰减系数反演模型。【拟解决的关键问题】通过Kd(490)=0.3 m-1对应的555 nm与443 nm波段处的遥感反射比值(Rrs(555)/Rrs(443)=1.3),将水体分成浑浊水域与清澈水域,并在浑浊水域处(Kd(490)>0.3 m-1,Rrs(555)/Rrs(443)>1.3)通过半分析算法的公式推导得到Kd(490), 而在清澈水域处(Kd(490) < 0.3 m-1,Rrs(555)/Rrs(443) < 1.3)利用统计的方法建立Kd(490)的经验算法,并最终将两算法结合,形成联合算法。
1 材料与方法 1.1 研究区域研究区域由渤海与黄海两个区域组成。渤海是中国大陆东部的边缘海,一面临海,三面环陆,是一个近封闭的内海,位于北纬37°07′~41°,东经117°35′~122°15′。渤海平均水深较浅,海底地势较为平缓,营养盐丰富,主要以软泥质和泥沙为主,其东部通过渤海海峡与黄海相通,沉积物以淤泥和粉沙淤泥为主。渤海的水质特征是自净能力低,水体浑浊度较高。黄海位于渤海东侧,南与东海相通,是太平洋西部的一个边缘海同时也是一个近似经向的半封闭浅海,位于北纬33°~41°,东经118°~127°。黄海海域的平均水深要大于渤海海域,且其沿岸地区有大量的河流入海口,潮差大、潮流急,自岸向海沉积物由粗到细呈带状分布。该海域的营养盐也较为丰富。
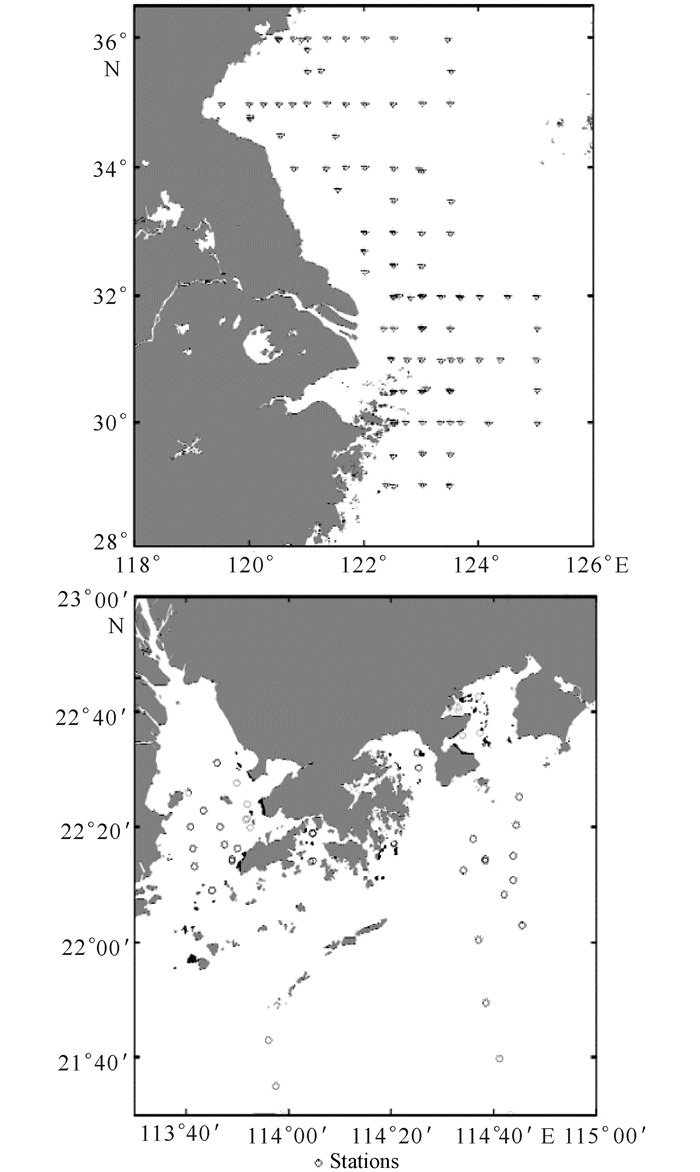
1.2 数据来源 1.2.1 现场实测资料238组实测数据的时间范围是2000年7月至2004年2月, 空间范围是黄东海与珠江口附近的海域。测量的参数包括在490 nm波段的漫衰减系数以及不同波段的遥感反射比等。建模采用的数据分布为2000年7月下旬与2001年2月上旬,珠江口海岸及其邻近海域22组;2001年3~5月,香港周围珠江口,博寮海及牛尾海49组;2002年4月、8月、9月、11月,东海区域46组;2003年春、秋季,黄、东海区域100组;2004年1月、2月,大亚湾和大鹏湾以东海区21组;采样站点如图 1所示。研究采集的数据时空跨度大,包含的水体类型复杂。
|
图 1 现场实测数据采集点[3] Fig.1 In-situ stations in Bohai and Yellow Seas |
中等分辨率成像频谱仪MERIS是目前水色传感器中最有优势的传感器之一,同时也是专门测量海洋及近岸水体水色的传感器,因此MERIS的主要作用是观测海水的颜色。MERIS传感器在可见光/近红外(390~1 040 nm),设置了15个波段,带宽范围3.75~20 nm,在可见光波段平均带宽为10 nm (文献[11])。本文选取卫星数据是2010年的Rrs(遥感反射比),其波段分别选取为443 nm, 490 nm, 560 nm, 665 nm, 709 nm。
1.3 数据分析方法以Matlab作为数据处理工具,以现场测量得到的数据为基础,首先通过半分析算法推导得出吸收系数a与后向散射系数bb, 进而计算出490 nm处的漫衰减系数。公式如下:
| $\begin{align} & {{K}_{\text{d}}}\left( \lambda \right)=\left( 1+0.005{{\theta }_{0}} \right)a\left( \lambda \right)+ \\ & 4.18\left\{ 1-0.52\exp \left[ -10.8a\left( \lambda \right) \right] \right\}{{b}_{\text{b}}}\left( \lambda \right) \\ \end{align}。$ | (1) |
在对半分析算法反演精度的分析过程中发现, 在Kd(490) < 0.3 m-1的区域内,反演结果出现了明显的低估现象。而基于前人的研究,Kd(490) < 0.3 m-1的区域可视为清澈水域,因此在Kd(490) < 0.3 m-1的区域内,以555 nm和443 nm波段的遥感反射比反演Kd(490)建立经验算法,并采用加权的方法将半分析算法与经验算法合并。
1.4 评价指标在上述数据分析的过程中,将所得到的实测数据进行划分,分别用于模型的建立和精度、稳定度的检验。检验模型精度需采用对数坐标下的决定系数(R2)、均方根误差(RMSE)与平均相对误差绝对值(MAPE),而用来判断模型稳定度则需采用均方根误差(RMSE)与平均相对误差绝对值(MAPE)。公式如下:
| $\text{RMSE=}\sqrt{\frac{\sum\limits_{i=1}^{n}{{{\left( {{x}_{i}}-{{y}_{i}} \right)}^{2}}}}{N}},$ | (2) |
| $MAPE=\frac{1}{N}\sum\limits_{i=1}^{n}{\left| \frac{{{x}_{i}}-{{y}_{i}}}{{{x}_{i}}} \right|}\times 100%,$ | (3) |
其中,y为反演值,x为实测值,N为样本数,i代表第i个样本。决定系数是相关系数的平方。
2 结果与分析 2.1 漫衰减系数半分析算法的建立后向散射系数bb(λ)通常可以表示为辐照度反射率与吸收系数a(λ)的函数[12-13]。Doran等[9]的研究表明,490 nm波段处的后向散射系数bb(490)与波长为709 nm的辐照反射率R (709)有着线性相关关系。基于此,将bb(490)同R (665)建立相关关系:
| ${{r}_{\text{rs}}}=\frac{{{R}_{\text{rs}}}}{0.52+1.7{{R}_{\text{rs}}}},$ | (4) |
| $R=\frac{n{{w}^{2}}}{{{t}^{2}}}Q{{R}_{\text{rs}}}\approx 1.89Q{{R}_{\text{rs}}},$ | (5) |
| ${{b}_{\text{b}}}\left( 490 \right)={{C}_{0}}+{{C}_{1}}R\left( 665 \right)。$ | (6) |
其中C0与C1可以被表示为
| ${{C}_{0}}={{b}_{\text{bw}}}\left( 490 \right)-\frac{{{b}_{\text{bp}}}\left( 490 \right)}{{{b}_{\text{bp}}}\left( 665 \right)}{{b}_{\text{bw}}}\left( 665 \right),$ | (7) |
| ${{C}_{1}}=\frac{{{b}_{\text{bp}}}\left( 490 \right)}{{{b}_{\text{bp}}}\left( 665 \right)}\frac{a\left( 665 \right)}{f\left( 665 \right)}。$ | (8) |
根据Babin等[14],假定
| $a\left( 665 \right)\approx {{a}_{\text{w}}}\left( 665 \right)。$ | (9) |
aw(λ)和bbw(λ)可参考Buiteveld等[15],
| ${{b}_{\text{bp}}}\left( 490 \right)=B\times {{b}_{\text{bp}}}\left( 710 \right),$ | (10) |
其中B为常数,取1.13。又因为
| $R\left( \lambda \right)=f\left( \lambda \right)\frac{{{b}_{\text{b}}}\left( \lambda \right)}{a\left( \lambda \right)},$ | (11) |
| ${{b}_{\text{b}}}\left( 710 \right)=\frac{R\left( 710 \right){{a}_{\text{w}}}\left( 710 \right)}{f\left( 710 \right)},$ | (12) |
| $\begin{align} & {{b}_{\text{bp}}}\left( 710 \right)={{b}_{\text{b}}}\left( 710 \right)-{{b}_{\text{bw}}}\left( 710 \right)= \\ & \frac{R\left( 710 \right){{a}_{\text{w}}}\left( 710 \right)}{f\left( 710 \right)}-{{b}_{\text{bw}}}\left( 710 \right), \\ \end{align}$ | (13) |
| ${{b}_{\text{b}}}\left( 665 \right)=\frac{R\left( 665 \right){{a}_{\text{w}}}\left( 665 \right)}{f\left( 665 \right)},$ | (14) |
| ${{b}_{\text{bp}}}\left( 665 \right)=\frac{R\left( 665 \right){{a}_{\text{w}}}\left( 665 \right)}{f\left( 665 \right)}-{{b}_{\text{bw}}}\left( 665 \right),$ | (15) |
| $\frac{{{b}_{\text{bp}}}\left( 490 \right)}{{{b}_{\text{bp}}}\left( 665 \right)}=\frac{B{{a}_{\text{w}}}\left( 665 \right)R\left( 710 \right)f\left( 665 \right)}{f\left( 710 \right){{a}_{\text{w}}}\left( 665 \right)R\left( 665 \right)}。$ | (16) |
由上述公式可得
| $\begin{align} & {{C}_{0}}=b{{a}_{\text{w}}}\left( 490 \right)-\frac{{{b}_{\text{bp}}}\left( 490 \right)}{{{b}_{\text{bp}}}\left( 665 \right)}={{b}_{\text{bw}}}\left( 490 \right)- \\ & \frac{B{{a}_{\text{w}}}\left( 665 \right)R\left( 710 \right)f\left( 665 \right)}{f\left( 710 \right){{a}_{\text{w}}}\left( 665 \right)R\left( 665 \right)}, \\ \end{align}$ | (17) |
| ${{C}_{1}}R\left( 665 \right)=\frac{B{{a}_{\text{w}}}\left( 665 \right)R\left( 710 \right)}{f\left( 710 \right)}。$ | (18) |
综上
| $\begin{align} & {{b}_{\text{b}}}\left( 490 \right)={{b}_{\text{bw}}}\left( 490 \right)- \\ & \frac{B{{a}_{\text{w}}}\left( 665 \right)R\left( 710 \right)f\left( 665 \right){{b}_{\text{bw}}}\left( 665 \right)}{f\left( 710 \right){{a}_{\text{w}}}\left( 665 \right)R\left( 665 \right)}+ \\ & \frac{B{{a}_{\text{w}}}\left( 665 \right)R\left( 710 \right)}{f\left( 710 \right)}, \\ \end{align}$ | (19) |
| $a\left( 490 \right)=\frac{f\left( 490 \right){{b}_{\text{b}}}\left( 490 \right)}{R\left( 490 \right)},$ | (20) |
其中f可视为常数,即f(λ)=0.335。
又由Lee等[16]提出的公式:
| ${{K}_{\text{d}}}\left( \lambda \right)=\left( 1+0.005{{\theta }_{0}} \right)a\left( \lambda \right)+4.18\left\{ 1-0.52\exp \left[ -10.8a\left( \lambda \right) \right] \right\}{{b}_{\text{b}}}\left( \lambda \right),$ | (21) |
联立(20)式、(21)式、(22)式可推导得到
| $\begin{align} & {{K}_{\text{dcb}}}=\left( 1+0.005{{\theta }_{0}} \right)\frac{f\left( 490 \right)}{R\left( 490 \right)}\left( {{b}_{\text{w}}}\left( 490 \right)- \right. \\ & \frac{B{{a}_{\text{w}}}\left( 665 \right)R\left( 710 \right)f\left( 665 \right){{b}_{\text{bw}}}\left( 665 \right)}{f\left( 710 \right){{a}_{\text{w}}}\left( 665 \right)R\left( 665 \right)}\text{+} \\ & \left. \frac{B{{a}_{\text{w}}}\left( 665 \right)R\left( 710 \right)}{f\left( 710 \right)} \right)\left( {{b}_{\text{w}}}\left( 490 \right)- \right. \\ & \frac{B{{a}_{\text{w}}}\left( 665 \right)R\left( 710 \right)f\left( 665 \right){{b}_{\text{bw}}}\left( 665 \right)}{f\left( 710 \right){{a}_{\text{w}}}\left( 665 \right)R\left( 665 \right)}\text{+} \\ & \left. \frac{B{{a}_{\text{w}}}\left( 665 \right)R\left( 710 \right)}{f\left( 710 \right)} \right) \\ \end{align}$ | (22) |
综上,我们可以利用现场测量得到的Rrs数据,推导得到Kdcb。
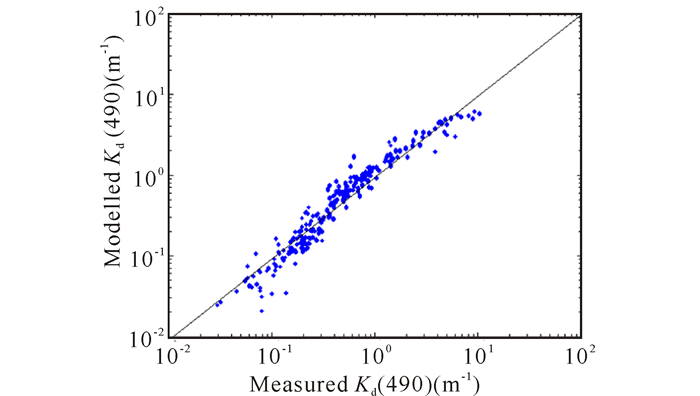
2.2 漫衰减系数半分析算法的检验利用238组数据对半分析算法反演结果进行精度检验,检验结果表明R2=0.888,RMSE=0.595 m-1, MAPE=27.01%。从图 2可以看出,虽然实测数据与反演结果具有较好的一致性,较好地分布在1:1的对角线上,但在Kd(490) < 0.3 m-1的区域出现了低估现象,该现象也可在表 1中直观看出。

|
图 2 利用半分析算法反演出的Kd(490)与实测的Kd(490)的对比散点图 Fig.2 Scatter diagram of the modelled and the measured Kd(490) |
| 表 1 半分析算法整体与分部精度比较 Table 1 The contrast between the accuracy of overall and parts of the semi-analytical algrorithm |
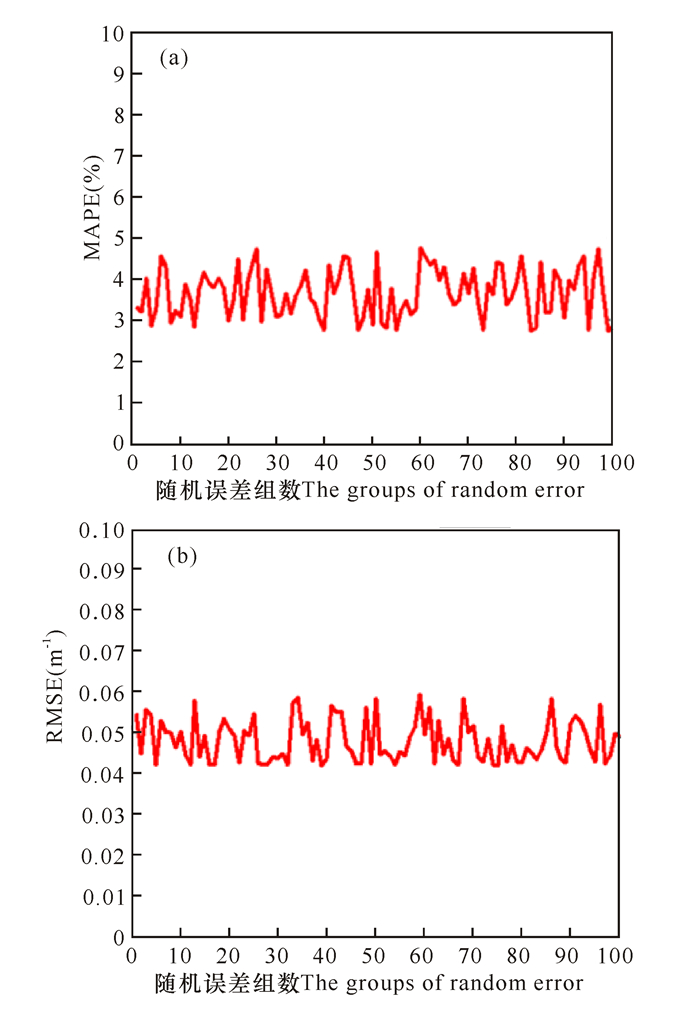
对半分析算法的稳定度检验时,引入100组平均值为0,标准差符合5%的正态分布来进行误差敏感性分析[17]。从图 3和图 4看出,模型反演结果MAPE在5%以内发生变化波动,RMSE则在0.06 m-1以内发生变化波动,说明该半分析的稳定性较好。
|
图 3 半分析算法误差敏感性分析 Fig.3 The test of sensitivity of the semi-analytical algrorithm |
|
图 4 半分析算法添加100组随机误差后MAPE (a)与RMSE (b)的变化波动 Fig.4 The variation of the MAPE (a) and RMSE (b) after adding 100 groups of random error to the semi-analytical algrorithm |
由2.2节分析可知,半分析算法在Kd(490) < 0.3 m-1的区域内(清澈水域)出现了明显的低估现象,因此尝试在Kd(490)的低值区采用统计的方法进行反演。
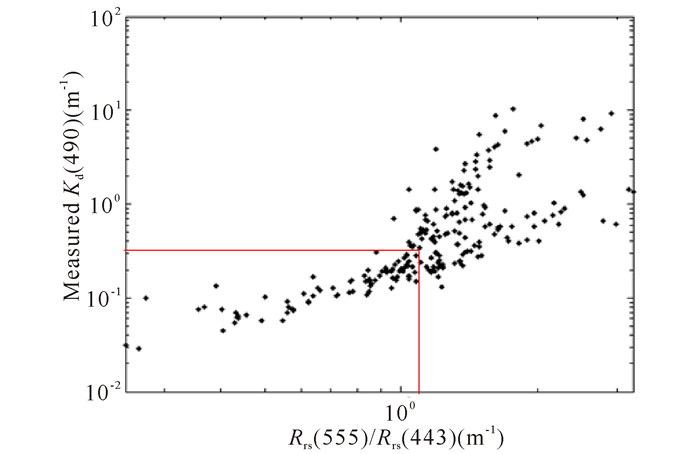
漫衰减系数与遥感反射比在特定的范围内存在明显的线性关系, 且从漫衰减系数同555 nm与443 nm波段处的遥感反射比(图 5),可以看出在Kd(490) < 0.3 m-1处(对应Rrs(555)/Rrs(443) < 1.3的范围内),两者之间存在着很好的线性相关。因此在Rrs(555)/Rrs(443)符合的范围内,建立Kd(490)的经验反演算法。
|
图 5 Kd(490)与Rrs(555)/Rrs(443)分布关系 Fig.5 The correlation of the Kd(490) and the ratio between Rrs(555) and Rrs(443) |
将符合条件数据中的70%的Rrs(555)/Rrs(443)与Kd(490)建立经验算法,算法可表示为
| $ {{K}_{\text{d}}}\left( 490 \right)=0.1453\times \left( {{R}_{\text{rs}}}\left( 555 \right)/{{R}_{\text{rs}}}{{\left( 443 \right)}^{0.6957}} \right)。$ |
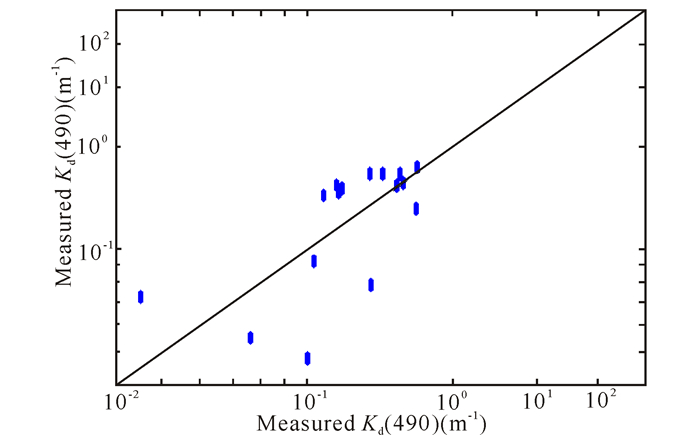
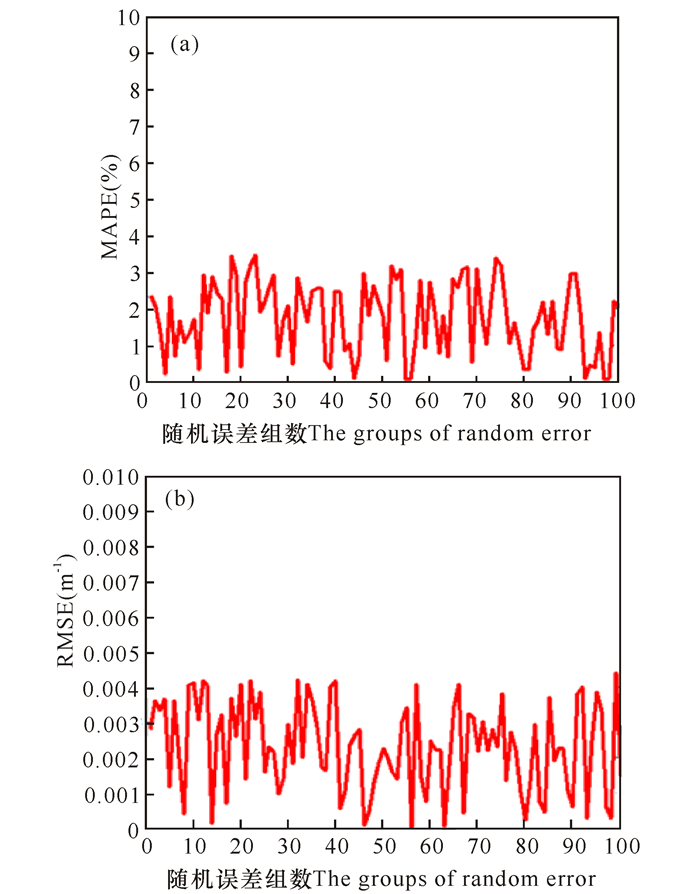
将剩余符合条件的30%的数据代入(22)式进行精度检验与模型误差敏感性分析检验,在清澈水域计算出经验算法的精度为R2=0.641,RMSE=0.021 m-1,MAPE=21.91%。模型误差敏感性分析如图 6、图 7所示。
|
图 6 经验算法误差敏感性检测 Fig.6 The test of the sensitivity of the empirical algrorithm |
|
图 7 经验算法添加100组随机误差后MAPE (a)与RMSE (b)的变化波动 Fig.7 The variation of the MAPE (a) and RMSE (b) after adding 100 groups of random error to the empirical algrorithm |
从图 6可以看到,引入100组随机误差以后的反演效果与未添加随机误差的反演效果差别不大。而图 7的结果表明,模型反演结果MAPE在3.5%以内发生变化波动,RMSE则在0.004 m-1以内发生变化波动,说明在清澈水域内该统计算法稳定。
此外通过与半分析方法Kd(490) < 0.3 m-1(Rrs(555)/Rrs(443) < 1.3)范围的精度比较发现:经验算法的精度与稳定度都有提高,因此决定在Rrs(555)/Rrs(443) < 1.3的范围内采用经验算法。
2.5 漫衰减系数联合算法的建立为了使Kd(490)在清澈水域与浑浊水域都有好的反演结果,将上述半分析算法与经验算法联合起来,并以Rrs(555)/Rrs(443)=1.05~1.5的区域作为算法的过渡区间,即当Rrs(555)/Rrs(443)>1.55时采用半分析算法;当Rrs(555)/Rrs(443) < 1.05时采用经验算法;当1.05 < Rrs(555)/Rrs(443) < 1.55时采用权重形式的算法。
采用经验算法的权重:
| $ {{\omega }_{1}}=\frac{1.5-x}{1.5-1.05}。$ |
半分析算法的权重:
| $ {{\omega }_{2}}=1-\frac{1.5-x}{1.5-1.05}。$ |
因此在过度区域处联合算法可表示为
| $ {{K}_{\text{dcb}}}={{w}_{1}}\times {{K}_{\text{dempirical}}}+{{w}_{2}}\times {{K}_{\text{dsemianalytical}}}。$ |
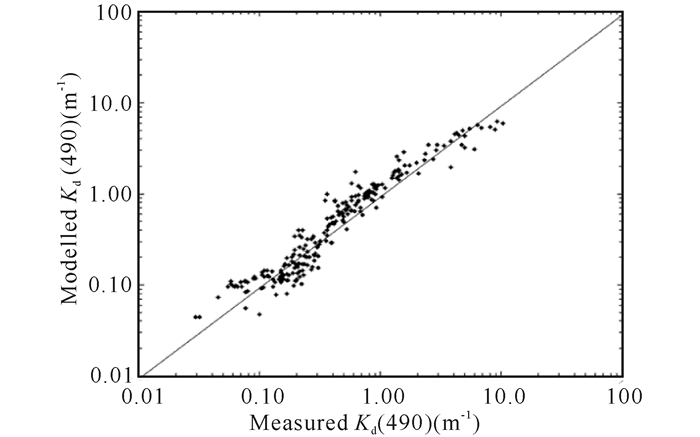
从图 8可以看出,算法结果与实测数据的散点很好地分布在1:1线附近。联合算法的精度为R2=0.891,RMSE=0.543 m-1,MAPE=26.77%。
|
图 8 联合算法反演结果与实测数据的比较 Fig.8 The contrast between the results of combined modelled and measured Kd(490) |
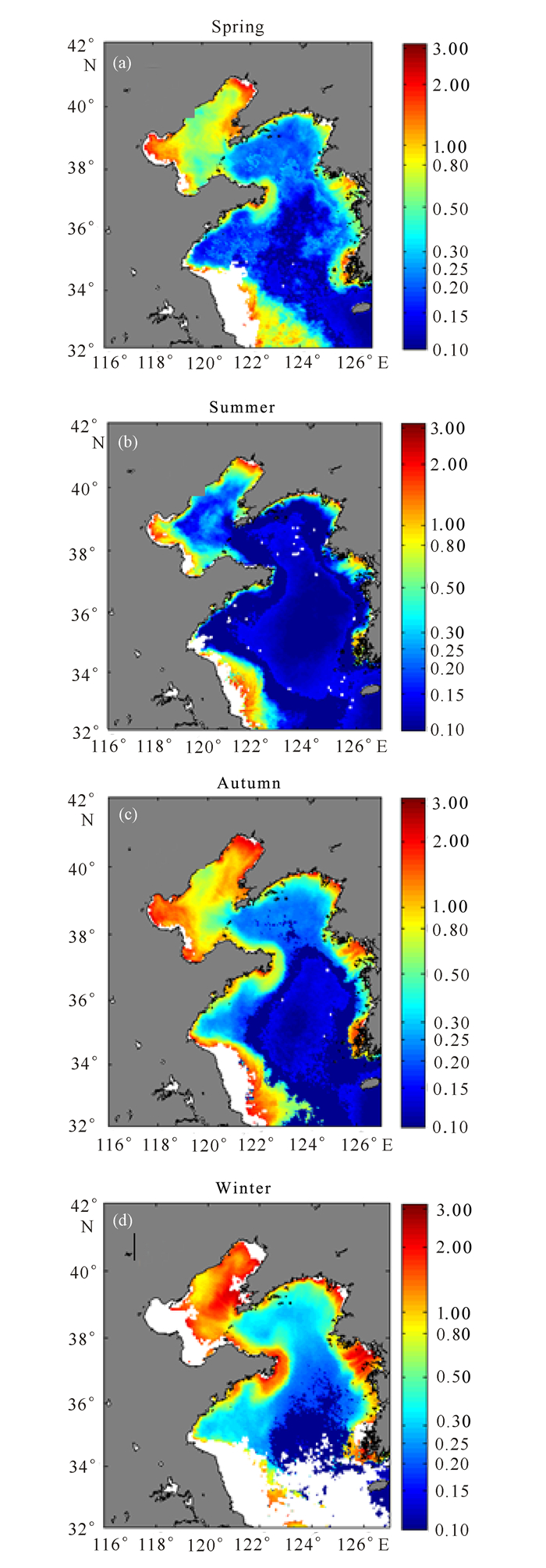
图 9(a~d)为基于2010年MERIS L3卫星遥感数据,并利用本文中的联合算法反演得到的渤黄海漫衰减系数Kd(490)的不同季节空间分布图。图 9(a~d)对应的季节分别为春、夏、秋、冬。
|
图 9 Kd(490)不同季节空间分布反演结果图(图中白色部分为缺测值) Fig.9 The variation of seasonal Kd(490) distribution (The part of white means NAN) |
从图 9可以看出Kd(490)的空间分布特点:从研究水域的沿岸向中心逐渐减小且渤海水域Kd(490)的值总体上要高于黄海水域Kd(490)的值。从春、夏、秋、冬4个季节的时间变化情况来看:春、夏季Kd(490)的低值区的范围要明显小于秋、冬季低值区的范围。这与现场实测到的漫衰减系数的时空分布范围变化情况一致。
3 结论本文基于现场实测数据,建立一个适用于不同水体类型的联合反演算法。(1)利用2000年7月至2004年2月在中国近海海域现场测量的238组光谱数据,分别在浑浊水域建立半分析算法,在清澈水域建立统计算法。(2)针对两种不同的算法,分别计算其精度,同时引入100组随机误差来检验算法的稳定度,进而将半分析算法与经验算法通过加权的方法进行结合,建立一种新的联合算法。检测结果表明:新建立的联合算法精度相对较高且稳定性好。最后利用MERIS卫星2010年的Rrs数据反演得到了漫衰减系数的季节变化与空间分布特征,其反演结果分布与实测漫衰减系数的时空分布基本一致。
本文的研究所针对的Kd(490)反演的区域限于以二类水体为主的渤黄海区域,因此联合算法的精度同半分析算法的精度相比提高不大;而且本研究建立的联合算法是否适用于更多水体类型的海域有待进一步的研究。
| [1] |
费尊乐. 近海水域漫衰减系数的估算[J]. 黄渤海海洋, 1984, 2(1): 26-29. FEI Z L. An estimation of the diffuse attenuation coefficient in offshore waters[J]. Journal of Oceanography of Huanghai & Bohai Seas, 1984, 2(1): 26-29. |
| [2] |
AUSTIN R W, PETZOLD T J. The determination of the diffuse attenuation coefficient of sea water using the coastal zone color scanner[J]. Oceanography from Space, 1981, 13: 239-256. |
| [3] |
AUSTIN R W, PETZOLD T J. Spectral dependence of the diffuse attenuation coefficient of light in ocean waters[J]. P Soc Photo-Opt Inst, 1984, 489: 168-178. |
| [4] |
MUELLER J L.SeaWiFS algorithm for the diffuse attenuation coefficient K (490) using water-leaving radiances at 490 and 555 nm[C]//HOOKER S S, FIRESTONE E R.SeaWiFS Postlaunch Calibration and Validation Analyses.Greenbelt, MD:NASA Goddard Space Flight Cent, 2000:24-27.
|
| [5] |
王晓梅, 唐军武, 丁静, 等. 黄海、东海二类水体漫衰减系数与透明度反演模式研究[J]. 海洋学报, 2005, 27(5): 38-45. WANG X M, TANG J W, DING J, et al. The retrieval algorithms of diffuse attenuation and transparency for the case-Ⅱ waters of the Huanghai Sea and the East China Sea[J]. Acta Oceanologica Sinica, 2005, 27(5): 38-45. |
| [6] |
张亭禄, 李肖霞. 基于人工神经网络的海水漫射衰减系数的遥感反演方法[J]. 中国海洋大学学报, 2007, 37(4): 676-680. ZHANG T L, LI X X. A Remote sensing method for the determination of seawater diffuse attenuation coefficient based on artificial neural networks[J]. Periodical of Ocean University of China, 2007, 37(4): 676-680. |
| [7] |
LEE Z P, CARDER K L, ARNONE R A. Deriving inherent optical properties from water color:A multiband quasi-analytical algorithm for optically deep waters[J]. Applied Optics, 2002, 41(27): 5755-5772. DOI:10.1364/AO.41.005755 |
| [8] |
LEE Z P, DARECKI M, CARDER K L, et al. Diffuse attenuation coefficient of downwelling irradiance:An evaluation of remote sensing methods[J]. Journal of Geophysical Research:Oceans, 2005, 110(C2): C02017. |
| [9] |
DORON M, BABIN M, MANGIN A, et al. Estimation of light penetration, and horizontal and vertical visibility in oceanic and coastal waters from surface reflectance[J]. Journal of Geophysical Research:Oceans, 2007, 112(C6): C06003. |
| [10] |
吴婷婷, 丘仲锋, 何宜军, 等. 黄东海及珠江口附近海域水体漫衰减系数反演[J]. 光学学报, 2013, 33(7): 154-162. WU T T, QIU Z F, HE Y J, et al. Retrieval algorithms of diffuse attenuation coefficient in the Yellow Sea, the East China Sea and the Pearl River Estuary[J]. Acta Optica Sinica, 2013, 33(7): 154-162. |
| [11] |
高中灵, 汪小钦, 陈云芝. MERIS遥感数据特性及应用[J]. 海洋技术, 2006, 25(3): 61-62. GAO Z L, WANG X Q, CHEN Y Z. The characteristic and applications of MERIS[J]. Ocean Technology, 2006, 25(3): 61-62. |
| [12] |
GORDON H R, BROWN O B. Diffuse reflectance of the ocean:Some effects of vertical structure[J]. Applied Optics, 1975, 14(12): 2892-2895. DOI:10.1364/AO.14.002892 |
| [13] |
GORDON H R, SMITH R C, ZANEVELD J R V.Introduction to ocean optics[C]//Proceedings of the SPIE 0486, Ocean Optics Ⅶ.Monterey:SPIE, 1980:1-43.
|
| [14] |
BABIN M, STRAMSKI D. Light absorption by aquatic particles in the near-infrared spectral region[J]. Limnology and Oceanography, 2002, 47(3): 911-915. DOI:10.4319/lo.2002.47.3.0911 |
| [15] |
BUITEVELD H, HAKVOORT J H M, DONZE M.The optical properties of pure water[C]//Proceedings of SPIE 2258, Ocean Optics XⅡ.Bergen, Norway:SPIE, 1994, 2258:174-183.
|
| [16] |
LEE Z P, DARECKI M, CARDER K L, et al. Diffuse attenuation coefficient of downwelling irradiance:An evaluation of remote sensing methods[J]. Journal of Geophysical Research:Oceans, 2005, 110(C2): C02017. |
| [17] |
陈亚慧, 丘仲锋, 孙德勇, 等. 黄渤海悬浮颗粒物粒径的遥感反演研究[J]. 光学学报, 2015, 35(9): 50-59. CHEN Y H, QIU Z F, SUN D Y, et al. Remote sensing of suspended particle size in Yellow Sea and Bohai Sea[J]. Acta Optica Sinica, 2015, 35(9): 50-59. |
 2016, Vol. 23
2016, Vol. 23 


