【研究意义】纳米晶体材料是近年的研究热点,在介观和宏观尺度,材料的性能很大程度由复杂的拓扑几何缺陷所决定[1-2]。这些缺陷起因于在原子尺度发生的复杂非平衡动力学方程[3-6]。金属材料的加工变形过程与位错的运动有着非常重要的关系。目前,材料微观结构的演化很难由实验实时观测到,因此,计算机模拟实验已成为了解和认识这些微观信息的重要手段和实验补充[7]。【前人研究进展】对材料变形的研究,现已深入到微纳观层次。Elder等[7-9]提出的晶体相场(Phase-field-crystal,PFC)方法,既可以描述晶体学结构特性以及原子尺度的行为,又可以揭示特征时间尺度为10-6秒量级的原子的缺陷运动行为。目前,PFC方法已有许多的成功应用[8-13]。【本研究切入点】在当前的实验条件下,对材料的纳米级行为很难原位观测[14],因此,发挥计算模拟实验的优势,应用其研究微纳米尺度的结构极为迫切和重要[15-17]。PFC方法能很好地用于描述晶界和位错在扩散时间尺度下的运动特征,并用于研究晶体在正应力作用下晶界与位错运动情况。【拟解决的关键问题】本研究应用PFC方法研究在施加正应力下的位错运动特征。
1 模型与方法 1.1 PFC方法系统无量纲的自由能函数可以写成
| $F=\int{\left\{ \frac{\rho }{2}\left[ \gamma +{{(1+{{\nabla }^{2}})}^{2}} \right]\rho +\frac{{{\rho }^{4}}}{4} \right\}}dr,$ | (1) |
式中,ρ为局域原子密度;r为与温度有关的唯象参数;∇2为拉普拉斯算子。在单模近似下,可以求得式子(1) 的一个稳定特解为
| $\rho =A[cos\text{ }\left( qx \right)cos\text{ }\left( \frac{qy}{\sqrt{3}} \right)\text{ }-\frac{1}{2}cos\text{ }\left( \frac{2qy}{\sqrt{3}} \right)\text{ }]+{{\rho }_{0}},$ | (2) |
式中,ρ0为平均原子密度,
本文采用保守场Cahn-Hilliard动力学方程[18]描述原子密度随时间的演化。该方程具体表示如下:
| $\frac{\partial \rho }{\partial t}={{\nabla }^{2}}\frac{\delta F}{\delta \rho }={{\nabla }^{2}}\left\{ {{\rho }^{3}}+[r+{{(1+{{\nabla }^{2}})}^{2}}\rho ] \right\},$ | (3) |
式中,ρ为局域原子密度,r表征体系的过冷度,∇2为拉普拉斯算子,t为时间变量。采用半隐式傅里叶伪谱方法[19-20],对无量纲动力学方程(3) 求解。
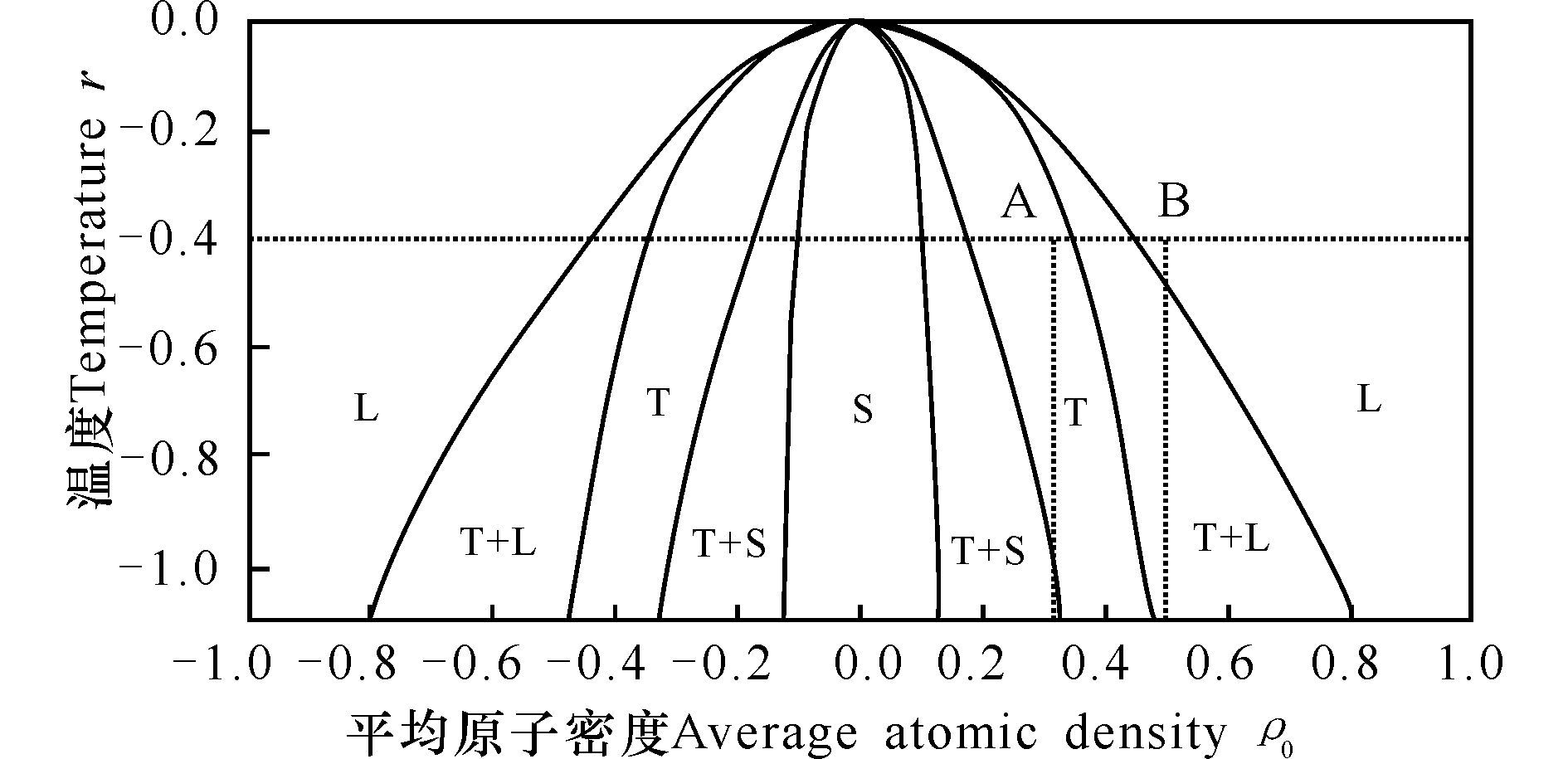
1.3 样品制备固相基体用三角相点阵表示,选取晶体平均原子密度参数为ρ0=0.344 2,温度参数r=-0.4(图 1点A)。计算模拟区域为512Δx×512Δy,单位格子长度Δx=Δy=π/4。模拟区域为双晶结构,左边晶界夹角为1°,右边晶界夹角为-1°,计算时四周边界采用周期性边界条件[16]。初始化的模拟样品如图 2a,弛豫50 000步后,模拟图如图 2b;上下分别加上40行的液相,液相的热力学参数设置为ρ01=0.446 0,温度参数r=-0.4(图 1点B),得到的模拟图如图 2c。空间步长随着应变速率在每一时间步长下都有一增量d=${\dot{\varepsilon }}$nΔt,其中,应变速率${\dot{\varepsilon }}$=6×10-6,n为时间步长数,Δt为时间步长,Δt=0.50。
|
L,液相;T,三角相;S,条状相 L,Liquid phase; T, Triangular phase; S, Strip phase 图 1 单模近似得到的二维相图 Fig.1 Two-dimensional phase diagram of the single mode approximation |

|
(a)初始样品;(b)弛豫后样品;(c)最终样品 (a)The initial sample;(b)The sample diagram of relaxation;(c)The diagram of final sample simulation 图 2 样品制备前中后模拟图 Fig.2 Simulation of sample preparation |
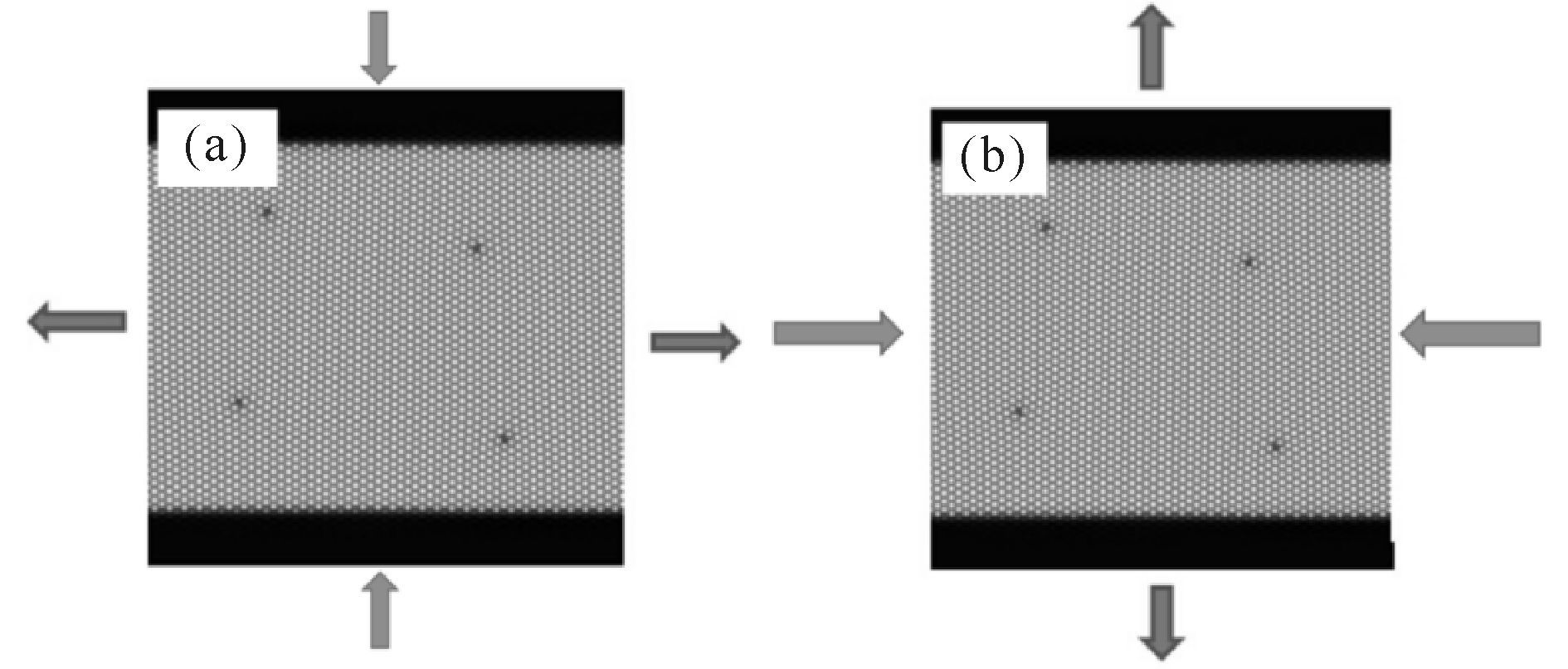
在中部加x向的拉应力(图 3a),位错运动的模拟演化图如图 4所示。可以看出,4个位错呈Z状移动,左边一组两个位错都向左上运动,同时右边一组两个位错向右下运动,随着时间的推移,两组位错先后进入到液相区域中,此时,中间区域成为完整单晶,再无位错存在。模拟初始时刻,固相区与液相区交界处是呈平直界面,位错进入液相区,此后,此界面不再平直,而是出现凹槽结构。
|
(a)x方向;(b)y方向 (a)The x direction;(b)The y direction 图 3 往x和y方向施加拉应力的位错运动趋势 Fig.3 The trend of the dislocation motion in the direction of x and y |

|
(a)t=55 000;(b)t=60 000;(c)t=65 000;(d)t=70 000;(e)t=75 000;(f)t=80 000 图 4 位错运动的模拟演化图 Fig.4 Simulation evolution of dislocation motion |
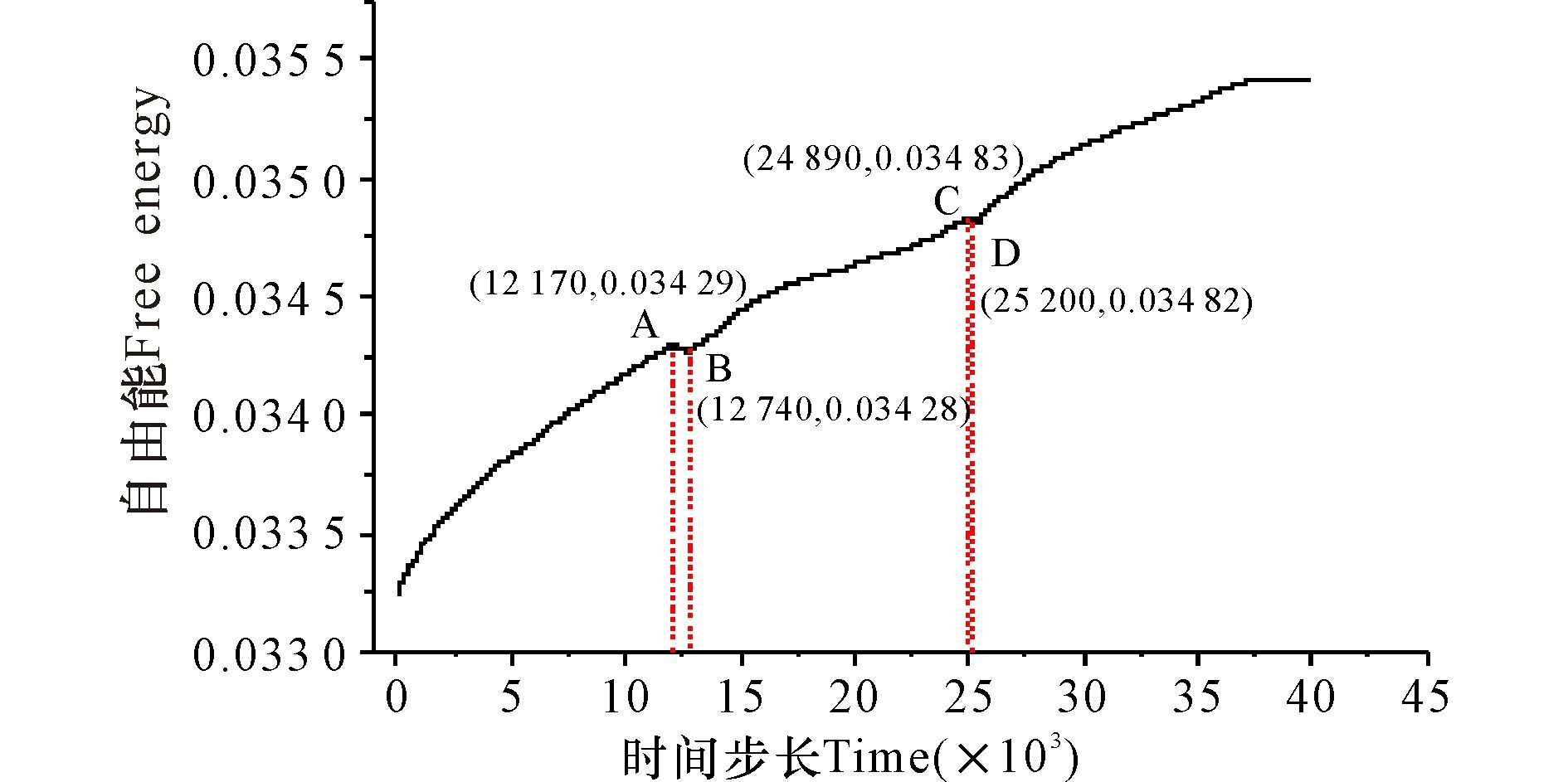
图 5自由能统计区域为刨开上下两部分的液相后的剩余中间部分固相区域。图 5点A是第一个极大值点即在t=12 170时,运动相反的两个位错刚好进入液相区时,位错内储存的弹性应变能得到释放,释放的弹性应变能大于增加的拉应变能,所以在点B即当t=12 740时整体自由能下降。从A→B自由能本来要上升,但是位错释放的弹性应变能使能量增加减缓。随着x方向拉应力的持续施加,体系自由能也持续上升。之后,直至剩下的运动方向相反的两个位错也进入到液相区,此时体系达到第二个极大值点C即t=24 890时,位错进入液相区后,它包含的弹性应变能得到释放,随着拉应力的持续施加,自由能也相应随之增加,跟A→B情况类似,C→D位错进入液相区释放的弹性应变能大于增加的拉应变能,所以C→D自由能下降。接着,从点D即t=25 200之后,随着x方向拉应力的持续施加,体系自由能也相应持续上升。
|
图 5 位错运动演化过程体系自由能变化曲线 Fig.5 Free energy change curve of the evolution of dislocation motion |
在中部加y向的拉应力(图 3b),位错运动的模拟演化图如图 6所示:此时运动情况与上一组正好相反,左边一组两个位错都向下运动,同时右边一组两个位错向上运动。随着时间的推移,两组位错先后进入到液相区域中。此时,中间区域成为完整单晶,再无位错存在。模拟初始时刻,固相区与液相区交界处是呈平直界面,位错进入液相区以后,与x轴拉应力所不同的是,此时界面处依然是平直界面。

|
(a)t=55 000;(b)t=60 000;(c)t=65 000;(d)t=70 000;(e)t=75 000;(f)t=80 000 图 6 位错运动的模拟演化图 Fig.6 Simulation evolution of dislocation motion |
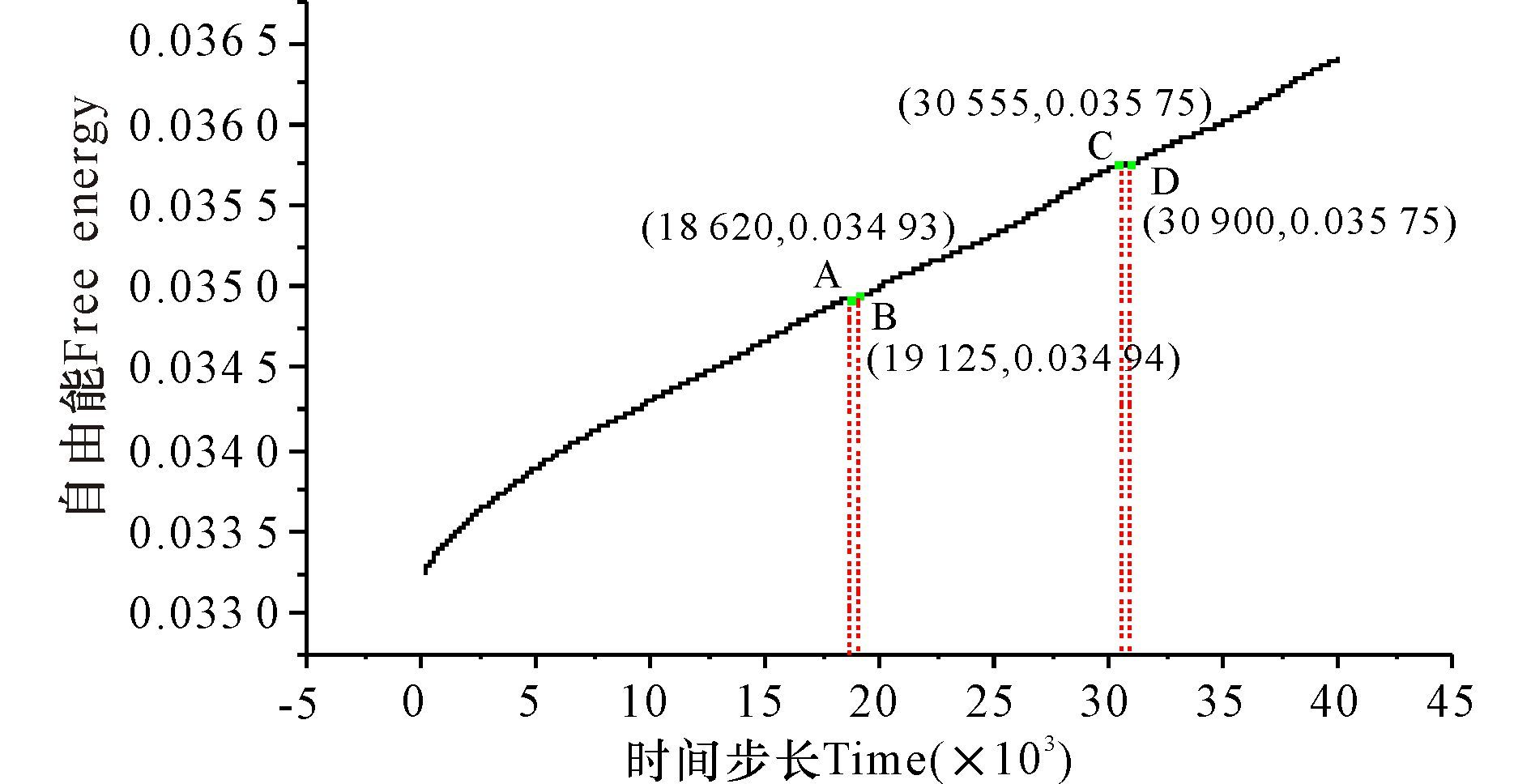
图 7自由能统计区域为刨开上下两部分的液相后的剩余中间部分固相区域。图 7点A是第一个极大值点即在t=18 620时运动相反的两个位错刚好进入液相区时,位错内储存的弹性应变能得到释放,释放的弹性应变能近似等于增加的拉应变能,所以在点B即当t=191 250时整体自由能保持不变,出现了类似“平台”的趋势。从A→B自由能本来要上升,但是位错释放的弹性应变能使能量增加减缓,所以出现了类似“平台”的趋势。随着y方向拉应力的持续施加,体系自由能也持续上升。之后,直至剩下的运动方向相反的两个位错也进入到液相区,此时体系达到第二个极大值点C,即t=30 555,位错进入液相区后,它包含的弹性应变能得到释放,随着拉应力的持续施加,自由能也相应随之增加,跟A→B情况类似,C→D位错进入液相区释放的弹性应变能近似等于增加的拉应变能,所以C→D也呈现类似“平台”结构。接着,从点D即t=30 900之后,随着y方向拉应力的持续施加,体系自由能也相应持续上升。
|
图 7 位错运动演化过程体系自由能变化曲线 Fig.7 Free energy change curve of the evolution of dislocation motion |
虽然拉应变是直接施加在样品上下左右边缘的原子层上,但是通过原子层间的耦合相互作用,可将拉应变逐层传递到刃型位错核心处作位错运动,继而导致攀移运动。由于位错进入液相区释放的弹性应变能与增加的拉应变能近似相等,所以使能量增加减缓。当沿x轴施加拉应力时,左边一列两对位错向左上运动,右边一列两对位错向右下运动。当沿y轴施加拉应力时,左边一列两对位错向左下运动,右边一列两队位错右上运动。可见改变拉应力的施加方向对位错的运动及自由能改变产生明显的影响。不论沿x轴还是y轴施加拉应变时,最终位错都运动到液相区,模拟区域成完整单晶,区域内再无位错存在。
| [1] |
秦河林, 陈建灵, 黄世叶, 等. 外应力作用下小角晶界的斜排位错运动研究[J]. 广西科学, 2015, 22(5): 506-510. QIN H L, CHEN J L, HUANG S Y, et al. Inclined dislocation motion of low angle grain boundaries under shear force exerting[J]. Guangxi Sciences, 2015, 22(5): 506-510. |
| [2] |
邵宇飞, 王绍青. 基于准连续介质方法模拟纳米多晶体Ni中裂纹的扩展[J]. 物理学报, 2010, 59(10): 7258-7265. SHAO Y F, WANG S Q. Quasicontinuum simulation of crack propagation in nanocrystalline Ni[J]. Acta Physica Sinica, 2010, 59(10): 7258-7265. |
| [3] |
LOEHNERT S, PRANGE C, WRIGGERS P. Error controlled adaptive multiscale XFEM simulation of cracks[J]. International Journal of Fracture, 2012, 178(1/2): 147-156. |
| [4] |
COLOMBO D, MASSIN P. Fast and robust level set update for 3D non-planar X-FEM crack propagation modelling[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(25/26/27/28): 2160-2180. |
| [5] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5): 051605. DOI:10.1103/PhysRevE.70.051605 |
| [6] |
刘晓骅, 叶里, 温振川, 等. 向错强度与阻尼系数对纳米晶材料小角度晶界湮没的影响[J]. 广西科学, 2015, 22(5): 511-516. LIU X H, YE L, WEN Z C, et al. Influence of disclination strength and damping coefficient on decay of low angle grain boundaries in nanocrystalline materials[J]. Guangxi Sciences, 2015, 22(5): 511-516. |
| [7] |
毛鸿, 罗志荣, 黄世叶, 等. 材料裂纹扩展分叉机理的晶体相场法研究[J]. 广西科学, 2015, 22(5): 499-505. MAO H, LUO Z R, HUANG S Y, et al. Phase-field-crystal modeling for crack propagation and branch of materials[J]. Guangxi Sciences, 2015, 22(5): 499-505. |
| [8] |
高英俊, 罗志荣, 邓芊芊, 等. 韧性材料的微裂纹扩展与分叉的晶体相场模拟[J]. 计算物理, 2014, 31(4): 471-478. GAO Y J, LUO Z R, DENG Q Q, et al. Phase-field-crystal modeling of microcrack propagation and branching in ductile materials[J]. Chinese Journal of Computational Physics, 2014, 31(4): 471-478. |
| [9] |
ARAFIN M A, SZPUNAR J A. A new understanding of intergranular stress corrosion cracking resistance of pipeline steel through grain boundary character and crystallographic texture studies[J]. Corrosion Science, 2009, 51(1): 119-128. DOI:10.1016/j.corsci.2008.10.006 |
| [10] |
CADINI F, ZIO E, AVRAM D. Monte Carlo-based filtering for fatigue crack growth estimation[J]. Probabilistic Engineering Mechanics, 2009, 24(3): 367-373. DOI:10.1016/j.probengmech.2008.10.002 |
| [11] |
刘晓波, 徐庆军, 刘剑. 铝裂纹扩展行为的分子动力学模拟[J]. 中国有色金属学报, 2014, 24(6): 1408-1413. LIU X B, XU Q J, LIU J. Molecular dynamics simulation of crack propagation behavior of aluminum[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 1408-1413. |
| [12] |
MA L, XIAO S F, DENG H Q, et al. Molecular dynamics simulation of fatigue crack propagation in bcc iron under cyclic loading[J]. International Journal of Fatigue, 2014, 68: 253-259. DOI:10.1016/j.ijfatigue.2014.04.010 |
| [13] |
STEFANOVIC P, HAATAJA M, PROVATAS N. Phase-field crystals with elastic interactions[J]. Physical Review Letters, 2006, 96(22): 225504. DOI:10.1103/PhysRevLett.96.225504 |
| [14] |
BERNAL F, BACKOFEN R, VOIGT A. Elastic interactions in phase-field crystal models:Numerics and postprocessing[J]. International Journal of Materials Research, 2010, 101(4): 467-472. DOI:10.3139/146.110296 |
| [15] |
ARAFIN M A, SZPUNAR J A. A new understanding of intergranular stress corrosion cracking resistance of pipeline steel[J]. Corros Sci, 2009, 51(1): 119-128. DOI:10.1016/j.corsci.2008.10.006 |
| [16] |
高英俊, 罗志荣, 黄创高, 等. 晶体相场方法研究二维六角相向正方相结构转变[J]. 物理学报, 2013, 62: 50507. GAO Y J, LUO Z R, HUANG C G, et al. Phase-field-crystal modeling for two-dimensional transformation[J]. Acta Physica Sinica, 2013, 62: 50507. |
| [17] |
高英俊, 罗志荣, 黄礼琳, 等. 韧性材料的微裂纹扩展和连通的晶体相场模[J]. 中国有色金属学报, 2013, 23: 1892. GAO Y J, LUO Z R, HUANG L L. Phase-field-crystal modeling for microcrack propagation and connecting of ductile materials[J]. Chin J Nonferrous Metals, 2013, 23: 1892. |
| [18] |
卢成健, 蒋丽婷, 王玉玲, 等. 晶体相场法模拟小角度晶界的位错结构及其演化[J]. 广西科学, 2013, 20(4): 316-320. LU C J, JIANG L T, WANG Y L, et al. Simulating structure of dislocation and its evolution in low angle grain boundary by phase-field-crystal method[J]. Guangxi Sciences, 2013, 20(4): 316-320. |
| [19] |
HIROUCHI T, TAKAKI T, TOMITA Y. Effects of temperature and grain size on phase-field-crystal deformation simulation[J]. Int J Mech Sci, 2010, 52: 309. DOI:10.1016/j.ijmecsci.2009.09.036 |
| [20] |
COLOMBO D, MASSINB P. Fast and robust level set update for 3D non-planar X-FEM crack propagation modelling[J]. Comput Method Appl M, 2011, 200: 2160-2180. DOI:10.1016/j.cma.2011.03.014 |
 2016, Vol. 23
2016, Vol. 23 


