【研究意义】晶界(Grain Boundary)是两个取向不同的相邻晶粒之间的交接界面[1]。通常晶界上的原子排列混乱、缺陷多、能量高,对材料力学性能影响较大[2]。对于一般金属,晶界对位错运动起阻碍作用。在室温下,对于一般金属材料晶界的存在本身就是一种强化因素。利用晶界的上述特性控制晶界的演化是目前的研究重点。由于晶界迁移等演化所涉及的时间尺度较小,在现有的实验条件下,很难直接被观察到。因此,计算机模拟实验成为重要的研究手段。【前人研究进展】近十来年采用计算机模拟材料的微观结构演化的方法有很多种,如分子动力学、蒙特卡洛方法、有限元分析方法等,此类方法在一定的尺度范围内模拟得出较好的结果。但是,分子动力学方法适用的特征时间尺度为10-14~10-12 s,对于扩散时间尺度(10-6 s)的微结构演化并不适合。晶体相场方法(PFC)[3-4]是近年来提出的一种新的材料模拟方法,它采用周期性原子密度函数为相场变量,通过密度场与温度场、应力场等外场的耦合,引入动力学方程。该方法可以分辨空间原子尺度及扩散时间尺度的材料微观结构演化。目前晶体相场方法已经被用于研究应力下的位错攀移和滑移[5-6],外延生长[7]、裂纹扩展[8-9]、晶界预熔化[10-11]等现象,模拟的结果与实验结果符合。在最初的PFC方法中,难以模拟空位缺陷结构,说明这个模型存在一定的局限性。为了弥补最初的PFC模型的不足,Chan等[12]引进一个空位自由能项限制参数范围(非负数)。修正后的VPFC模型及其相图也随之发生变化,出现空位相。【本研究切入点】对比PFC与VPFC两个模型在模拟位错运动演化过程中的现象,得出模型差异,运用VPFC模型模拟材料微观结构演化。【拟解决的关键问题】通过添加空位自由能项修正晶体相场模型(PFC model),得到空位晶体相场法模型(VPFC model),并采用VPFC模型模拟在外加单方向应力作用下小角度晶界的变形过程。
1 模型与方法 1.1 模型介绍最早的晶体相场模型是由Elder等[3-4]在2004年提出的,它基于密度泛函理论得到的原子密度函数ρ作为序参量,以该序参量构建的自由能表达式为[3]
| $F=\int{\left\{ \frac{\rho }{2}\left[ \gamma +{{(1+{{\nabla }^{2}})}^{2}} \right]\rho +\frac{{{\rho }^{4}}}{4} \right\}}dr,$ | (1) |
式中,r是无量纲化的温度参数,q是原子间距。增加了空位自由能项fv ac(ρ)后,系统总自由能变为
| $F=\int{\left\{ \frac{\rho }{2}\left[ \gamma +{{(1+{{\nabla }^{2}})}^{2}} \right]\rho +\frac{{{\rho }^{4}}}{4}+{{f}_{v\text{ }ac}}\left( \rho \right) \right\}}dr,$ | (2) |
其中空位自由能表达式为[13]
| ${{f}_{v\text{ }ac}}\left( \rho \right)=H({{\rho }^{n}}-|{{\rho }^{n}}|),$ | (3) |
式中取n=3,H=1 500,空位自由能表达式是一个分段函数,当ρ>0时,空位自由能为0;当ρ<0时,空位自由能为较大的正值。因此,这一空位项消弱了ρ的负值。这使得空位晶体相场模型组成的周期结构与规则晶体相场模型有一些不同。与传统晶体相场模型一样,空位晶体相场也采用C-H方程[14]控制原子密度函数随时间的演化:
| $\frac{\partial \rho \left( x,t \right)}{\partial t}=\alpha {{\nabla }^{2}}\frac{\delta F\left[ \rho \right]}{\delta \rho \left( x,t \right)},$ | (4) |
将原子密度函数代入到自由能表达式中,求出六角晶格自由能函数极小值,得到平衡时六角晶格的单模原子密度函数:
| $\rho =A[cos\text{ }\left( qx \right)cos\text{ }\left( \frac{qy}{\sqrt{3}} \right)\text{ }+\frac{1}{2}cos\text{ }\left( \frac{2qy}{\sqrt{3}} \right)\text{ }]+{{\rho }_{0}},$ | (5) |
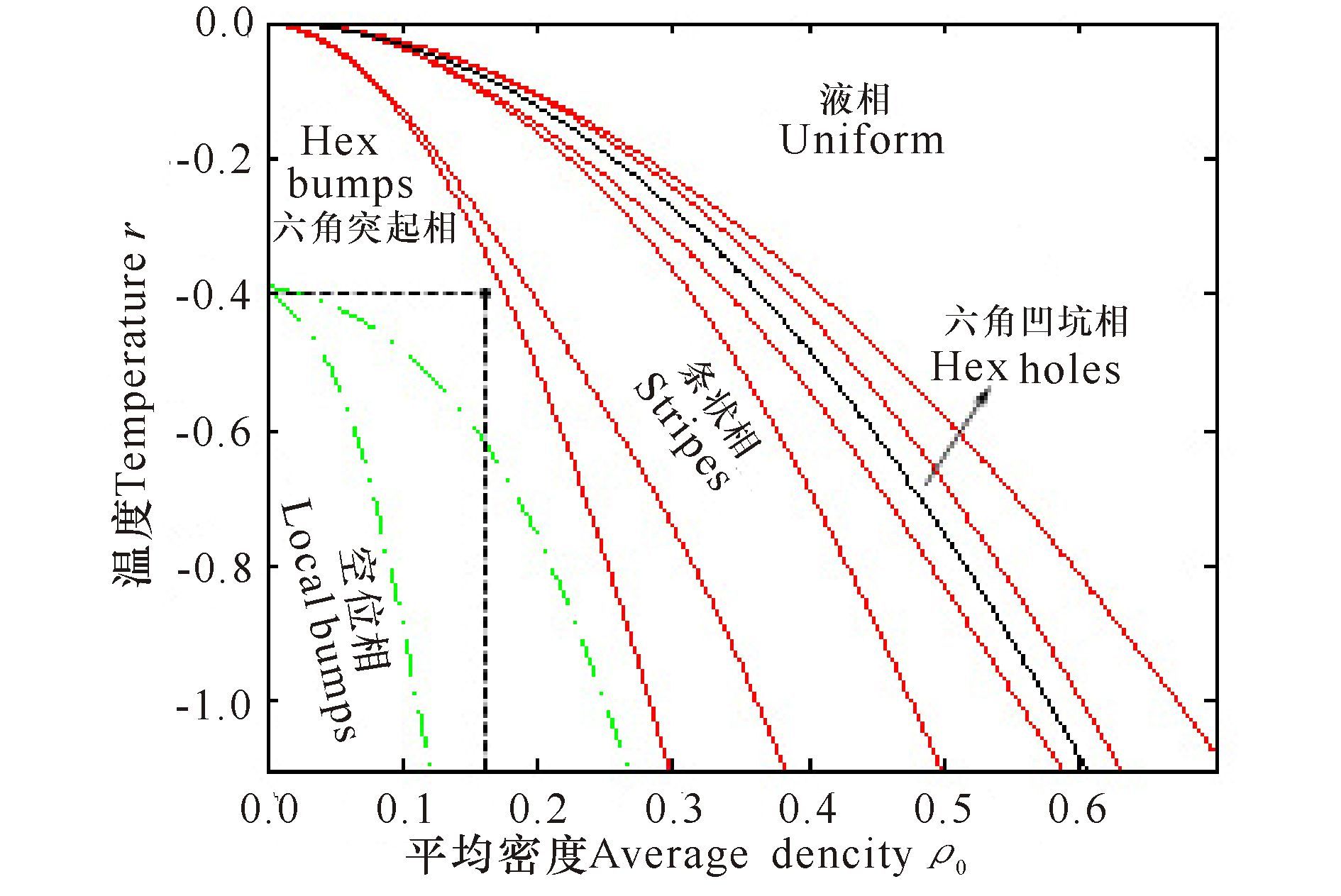
式中A为密度振幅,q为原子间距,ρ0为平均密度。二维VPFC模型相图[12]如图 1所示。
|
图 1 二维VPFC相图 Fig.1 Two-dimensional phase diagram of vacancy phase-field-crystal |
设置一个大小为Lx*Ly=512*512的样品,空间步长设置为Δx=Δy=1,时间步长设置为Δt=0.007 5。采用周期性边界条件。设置样品初始条件:在样品0<x<Lx/4和3Lx/4<x<Lx的范围内晶粒取向为θ/2,在Lx/4<x<3Lx/4范围内的晶粒取向为-θ/2(图 2a)。经过一段时间(设置弛豫时间步数为100 000步)演化,系统达到稳定(图 2b)。

|
图 2 样品设置(a)及弛豫过程的体系自由能变化过程(b) Fig.2 Prepared sample(a) and the free energy of system for relaxation process (b) |
给样品施加不同方向的拉和压应力,采用VPFC模型模拟晶界上的位错在应变作用下的运动过程,参数见表 1,其中θ为晶界取向差角,r为温度参数,ρ0为原子平均密度,E为应变率。
| 表 1 样品制备参数 Table 1 Parameters of sample preparation |
在外应变条件下,晶界上的位错会因晶粒的变形而运动,通过公式(2) ,计算整个加应变过程系统的自由能变化,并绘制系统自由能变化曲线;在曲线关键的位置选取对应的晶粒演化图进行分析,并对每一个位错进行编号;最后,对两个样品的晶粒晶列取向(二维)进行简化分析。
2 结果与分析 2.1 A1组实验如图 3所示,通过对自由能曲线和演化图的分析,可将演化过程分为4个阶段。第1阶段(图 3a~b),位错组在应变作用下攀移,两个晶粒的取向差稍微减小。当应变达到0.108 0(900 000步左右)时,左边1号位错组滑移出来,其余位错组继续攀移。第2阶段(图 3b~e),系统应变继续增加,左右晶界的位错组都出现滑移。首先是左边位错组5向左滑移,随后右边的晶界上位错组6,9和10都向右边滑移出来。剩余位错组还在晶界上继续攀移。此外,通过观察位错组1和位错组2,对比得出位错组攀移速度远小于滑移速度。第3阶段(图 3e~f),停留晶界上的位错继续攀移,系统自由能累积上升。第4阶段(图 3f~i),原左边晶界上的位错组1至5都滑移到右边晶界的附近停留(图 3i)。而右边晶界上的位错组也有部分滑移到原来左边晶界的位置,这时晶粒1,2的取向差明显减小。位错组4到达右边晶界的位置后继续向下攀移,攀移方向与位错组8相反,最后两个位错组相遇湮没。

|
(a)T=0 (ε=0) ;(b)T=1 096 000(ε=0.131 5) ;(c)T=1 270 000(ε=0.152 4) ;(d) T=1 380 000 (ε=0.165 6) ;(e)T=1 601 000 (ε= 0.192 1) ;(f)T=1 899 000(ε=0.227 8) ;(g)T=2 023 000(ε= 0.242 7) ;(h)T=2 260 000(ε= 0.271 2) ;(i)T=2 322 000(ε=0.278 6) ;(j)T=2 352 000(ε=0.282 2) ;曲线上的点A~J分别对应着演化图(a~j);黄色箭头表示位错运动方向 The points on the curve A~J correspond to the evolution diagram (a~j);The yellow arrow indicates the direction of the movement of the dislocation 图 3 加x方向拉应变样品演化过程(a~j)及系统自由能变化(k) Fig.3 Evolutionary process of sample with tensile stress at x-direction (a~j)and the free energy of system(k) |
从能量的角度分析,图 3k自由能曲线中的点A~J分别对应于图 3a~j。原子相互作用能可以分为畸变能和原子势能。在原子数量和相对位置不变的情况下,原子势能基本保持不变,系统能量变化的主要贡献是畸变能。在第1阶段,位错受应变的作用沿着晶界攀移,系统畸变能增加,对应的自由能曲线能量呈上升趋势,在1号位错组滑移出晶界后,系统自由能上升变慢。这是由于位错滑移出晶界后,晶界上的位错组密度减小,畸变能也随之减小。第2阶段,点B位置自由能开始下降。对应的演化图 3b中,晶界上的位错组不断滑移出去,晶界上的畸变变小,系统总自由能迅速下降,对应图 3k曲线上的点B~E。第3阶段,晶界上的位错继续攀移,能量积累,曲线呈上升趋势,对应能量曲线上的点E和F。第4阶段,位错4和位错8相遇湮没减少了样品的畸变,系统自由能出现微小的下降(图 3k中的点F~G)。
2.2 A2组实验对样品施加x方向的压应力得到如图 4的演化过程,在这一过程中,位错组只在x方向压应力作用下做攀移运动,并没有出现位错组滑移现象。而自由能曲线也出现明显的拐点(自由能曲线中的C、D两点)。图 4c中,在位错10的左右两边出现新的缺陷(图中的放大区域),然后形成一对柏氏矢量相反的位错组,最后在应力的作用下沿晶列方向滑移(图 4d中的红色位错)。注意到,位错组攀移的方向与A1样品(受x方向拉应力)结果中攀移方向相反。

|
(a)T=0(ε=0) ;(b)T=1 250 000(ε=0.105 0) ;(c)T=1 730 000(ε=0.207 6) ;(d) T=1 916 000(ε=0.229 9) ;曲线上的点A~J分别对应着演化图(a~j);黄色箭头表示位错运动方向 The points on the curve A~J correspond to the evolution diagram (a~j);The yellow arrow indicates the direction of the movement of the dislocation 图 4 加x方向压应变作用样品的演化过程(a~d)及系统自由能变化(e) Fig.4 Evolutionary process of sample with compression stress at x-direction (a~d) and the free energy of system(e) |
如图 5a~b所示,虚线表示晶列方向,粗箭头表示受力方向,细箭头表示位错组攀移方向。T型符号表示位错组符号,即两个单刃型位错组成的位错组可以等效为他们柏氏矢量总和的效果(图 5c),具体公式为[5]
| ${{b}_{1}}+{{b}_{2}}=d\theta n=B,$ | (6) |

|
图 5 样品左边晶界受x方向应力的简化图(a~b)及位错组柏氏矢量合成图[16](c) Fig.5 Simplified diagrams of the left boundary simple with x-direction stress (a~b) and the diagram of dislocations Burgers vector composition[16](c) |
由图 5a可知,样品受到x方向压应力作用,原子在位错下方聚集,这时位错的半原子面向上增加,则位错向上攀移。图 5b中,晶列受x方向拉应力作用,晶界两边的晶粒取向差变小,位错的半原子面向下运动,则位错向下攀移。根据位错间距d与柏氏矢量B、晶粒取向差θ的关系:
| $d=\frac{B}{2sin\text{ }\left( \frac{\theta }{2} \right)}\text{ }\approx \frac{B}{\theta },$ | (7) |
取向差变小,位错间距变大,则晶界上的位错密度变小,在没有位错反应的情况下,位错滑移出晶界以减小位错密度。
在文献[6]中,作者采用PFC模型模拟双晶界在应力作用下的位错演化实验,观察到x方向拉应力和y方向拉应力的不同导致位错攀移的方向也不同,因为拉应力促使负攀移的发生,而压应力则会促使正攀移的发生。本研究中我们可以将样品受x方向压应力与受y方向拉应力的效果等效,研究得到的结果表明,x方向的拉应力和x方向的压应力在初始阶段位错组攀移分别为负攀移和正攀移,与PFC模型模拟的结果相似。
VPFC模型的优势在于模拟空位结构,这是目前PFC模型所不能模拟研究的微观结构。在最近一些采用PFC模型模拟空位-裂纹扩展的文献中,空位内的密度值并非最低值,而是接近平均原子密度值。而VPFC模型模拟得到的空位结构[15],空位内的密度值是最低的零,更接近现实。
3 结论本研究采用VPFC模型模拟双晶界在单向应变的作用下位错运动情况,揭示不同应力形式对位错攀移和位错反应的影响。结果表明,样品受x方向的拉应力促使晶界上的位错在初始阶段发生负攀移,随后位错滑移并与其他位错相遇湮灭或合并;样品受x方向压应力促使晶界上的位错在初始阶段反生正攀移,位错没有滑移。VPFC模型的优势是模拟空位结构,这一模型研究空位结构上的演化将会继续得以应用。
| [1] |
余永宁. 材料科学基础[M]. 北京: 高等教育出版社, 2006. YU Y N. Fundamentals of Materials Science[M]. Beijing: Higher Education Press, 2006. |
| [2] |
王吉会, 郑俊萍, 刘家臣, 等. 材料力学性能[M]. 天津: 天津大学出版社, 2006. WANG J H, ZHENG J P, LIU J C, et al. Mechanical Behavior of Materials[M]. Tianjin: Tianjin University Press, 2006. |
| [3] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5): 051605. DOI:10.1103/PhysRevE.70.051605 |
| [4] |
ELDER K R, KATAKOWSKI M, HAATAJA M, et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88(24): 245701. DOI:10.1103/PhysRevLett.88.245701 |
| [5] |
高英俊, 黄礼琳, 周文权, 等. 高温应变下的亚晶界湮没与位错旋转机制的晶体相场模拟[J]. 中国科学:技术科学, 2015, 45(3): 306-321. GAO Y J, HUANG L L, ZHOU W Q, et al. Phase field crystal simulation of subgrain boundary annihilation and dislocation rotation mechanism under strain at high temperature[J]. Scientia Sinica Technologica, 2015, 45(3): 306-321. |
| [6] |
杨涛, 陈铮, 董卫平. 应力诱发双位错组亚晶界湮没的晶体相场模拟[J]. 金属学报, 2011, 47(10): 1301-1306. YANG T, CHEN Z, DONG W P. Phase field crystal simulation of stress-induced annihilation of sub-grain boundary with double-array dislocation[J]. Acta Metallurgica Sinica, 2011, 47(10): 1301-1306. |
| [7] |
黄礼琳, 华平, 王玉玲, 等. 凸曲率衬底外延生长界面演化的晶体相场模拟[J]. 广西科学, 2014, 21(3): 241-246. HUANG L L, HUA P, WANG Y L, et al. Simulation of epitaxial growth interface on convex substrate using phase field crystal method[J]. Guangxi Sciences, 2014, 21(3): 241-246. |
| [8] |
郭刘洋, 陈铮, 龙建, 等. 晶体相场法研究应力状态及晶体取向对微裂纹尖端扩展行为的影响[J]. 物理学报, 2015, 67(17): 0178102. GUO L Y, CHEN Z, LONG J, et al. Study on the effect of stress state and crystal orientation on micro-crack tip propagation behavior in phase field crystal method[J]. Acta Physica Sinica, 2015, 67(17): 0178102. |
| [9] |
高英俊, 罗志荣, 邓芊芊, 等. 韧性材料的微裂纹扩展与分叉的晶体相场模拟[J]. 计算物理, 2014, 31(4): 471-478. GAO Y J, LUO Z R, DENG Q Q, et al. Phase-field-crystal modeling of microcrack propagation and branching in ductile materials[J]. Chinese Journal of Computational Physics, 2014, 31(4): 471-478. |
| [10] |
周文权, 黄世叶, 王震, 等. 高温应变作用下小角度晶界湮没过程的晶体相场模拟[J]. 广西科学, 2014, 21(3): 247-251. ZHOU W Q, HUANG S Y, WANG Z, et al. Phase field crystal simulation of annihilation process of small-grain boundary under stress at high temperature[J]. Guangxi Sciences, 2014, 21(3): 247-251. |
| [11] |
高英俊, 周文权, 邓芊芊, 等. 晶体相场方法模拟高温应变作用的预熔化晶界的位错运动[J]. 金属学报, 2014, 50(7): 886-896. GAO Y J, ZHOU W Q, DENG Q Q, et al. Phase field crystal simulation of strain effects on dislocation movement of premelting grain boundries at high temperature[J]. Acta Metallurgica Sinica, 2014, 50(7): 886-896. |
| [12] |
CHAN P Y, GOLDENFELD N, DANTZIG J. Molecular dynamics on diffusive time scales from the phase-field-crystal equation[J]. Physical Review E, 2009, 79(3): 035701. DOI:10.1103/PhysRevE.79.035701 |
| [13] |
BERRY J, GRANT M. Modeling multiple time scales during glass formation with phase-field crystals[J]. Physical Review Letters, 2011, 106(17): 175702. DOI:10.1103/PhysRevLett.106.175702 |
| [14] |
YU Y M, BACKOFEN R, VOIGT A. Morphological instability of heteroepitaxial growth on vicinal substrates:A phase-field crystal study[J]. Journal of Crystal Growth, 2011, 318(1): 18-22. DOI:10.1016/j.jcrysgro.2010.08.047 |
| [15] |
ROBBINS M J, ARCHER A J, THIELE U, et al. Modeling the structure of liquids and crystals using one- and two-component modified phase-field crystal models[J]. Physical Review E, 2012, 85(6): 061408. DOI:10.1103/PhysRevE.85.061408 |
| [16] |
高英俊, 卢成健, 黄礼琳, 等. 晶界位错运动与位错反应过程的晶体相场模拟[J]. 金属学报, 2014, 50(1): 110-120. GAO Y J, LU C J, HUANG L L, et al. Phase field crystal simulation of dislocation movement and reaction[J]. Acta Metallurgica Sinica, 2014, 50(1): 110-120. |
 2016, Vol. 23
2016, Vol. 23 


