【研究意义】材料在生产制造和实际应用的过程中,受加载作用下容易产生微裂纹,这些微裂纹在一定的条件下会发生扩展,从而影响材料的寿命[1]。早期的研究是从材料断裂的宏观表象出发,建立了断裂力学理论和模型,来解释裂纹萌生和扩展的相关行为[2]。但实际上,裂纹的萌生与扩展[3]在纳米尺度就开始了。因此,深入研究材料的断裂特征,就不能只停留在给出表象的宏观尺度上,而应当从纳观尺度分析裂纹萌生与扩展机理。【前人研究进展】材料在介观和宏观尺度上的性能,在很大程度上由其内部的微观缺陷所决定[4],例如:空洞、空位、位错、晶界以及微裂纹等。这些缺陷起因于在原子尺度发生的复杂非平衡动力学过程[5]。就目前所采用的多尺度模拟研究方法来说,对这些微观特征结构的实时演化过程的建模和模拟是一个重大的挑战。最近,Elder等[5-7]基于密度泛函理论提出了晶体相场(phase-field-crystal,PFC)模型。该模型给出了新的自由能函数形式,引入周期序参量作为局域密度场,它将无序相(液相等)的密度场定义为一常数,将固相的密度场表示成周期性函数(波)的形式,进而通过周期的原子密度函数表现晶体的周期结构。这样的密度场就很自然地与弹性效应、晶粒取向和位错的运动等由周期性结构产生的物理特性紧密的关联起来[8]。目前,PFC方法已有许多具体的应用,例如:模拟位错滑移和攀移[9]、相结构转变[10]、异质外延生长[11]、纳米晶粒长大[12]等。【本研究切入点】材料微裂纹扩展的研究目前主要集中在材料受到外部载荷累计改变作用下的疲劳裂纹尖端扩展行为以及裂纹分叉特性[13-14],而应用先进的PFC模型,研究初始缺口尺寸大小对裂纹起裂影响的工作还鲜有报道。【拟解决的关键问题】应用PFC方法模拟拉伸应变作用下[15],纳米级裂纹起裂的动态演化过程,详细分析预制中心缺口尺寸大小对裂纹起裂的影响。
1 PFC模型与方法 1.1 体系的自由能密度函数与传统的相场模型不同,PFC模型采用具有周期性的局域原子密度场作为相场变量[6]。因此,PFC模型能够反映晶体周期结构特性以及原子尺度的行为。对于固态金属材料,其原子的位置不依赖于时间,呈现规则排列。文献[6]给出了既能够描述晶体周期结构,又能描述体系均匀结构的密度函数,其表达式可写成
| $\rho \left( r,t \right)=\sum\limits_{n,m}{{{a}_{n,m}}}{{e}^{G\cdot r}}+{{\rho }_{0}},$ | (1) |
式中,G为倒格子,r为空间位置矢量,an,m为Fourier系数。式(1) 中等号右边第一项反映晶格原子的周期性排列特征;第二项ρ0反映均匀无序相的原子密度分布平均值,是一个常量。此时体系无量纲的自由能函数F可以写成
| $F=\int{\left\{ \frac{\rho }{2}\left[ \gamma +{{(1+{{\nabla }^{2}})}^{2}} \right]\rho +\frac{{{\rho }^{4}}}{4} \right\}}dr,$ | (2) |
式中:γ为与体系温度相关的参数,∇2为Laplace算子。该自由能函数自洽地包含了晶体周期结构的物理特征,例如:多晶取向、弹性效应、塑性变形等。对体系的极小自由能函数的二维解作单模近似,可得到平衡时三角格子相的原子密度场变量ρ,其单模形式[16]可写成
| $\rho \left( x,y \right)={{A}_{0}}[cos\text{ }\left( qx \right)cos\text{ }\left( \frac{qy}{\sqrt{3}} \right)\text{ }-\frac{1}{2}cos\text{ }\left( \frac{2qy}{\sqrt{3}} \right)\text{ }]+{{\rho }_{0}},$ | (3) |
式中:A0是一个特定的常数,反映固相原子密度周期结构的振幅。由能量函数取极小值得到:波矢q=2π/a,A0表达式为
| ${{A}_{0}}=\frac{4}{5}({{\rho }_{0}}+\frac{1}{3}\sqrt{-15r-36{{\rho }_{0}}^{2}}),$ | (4) |
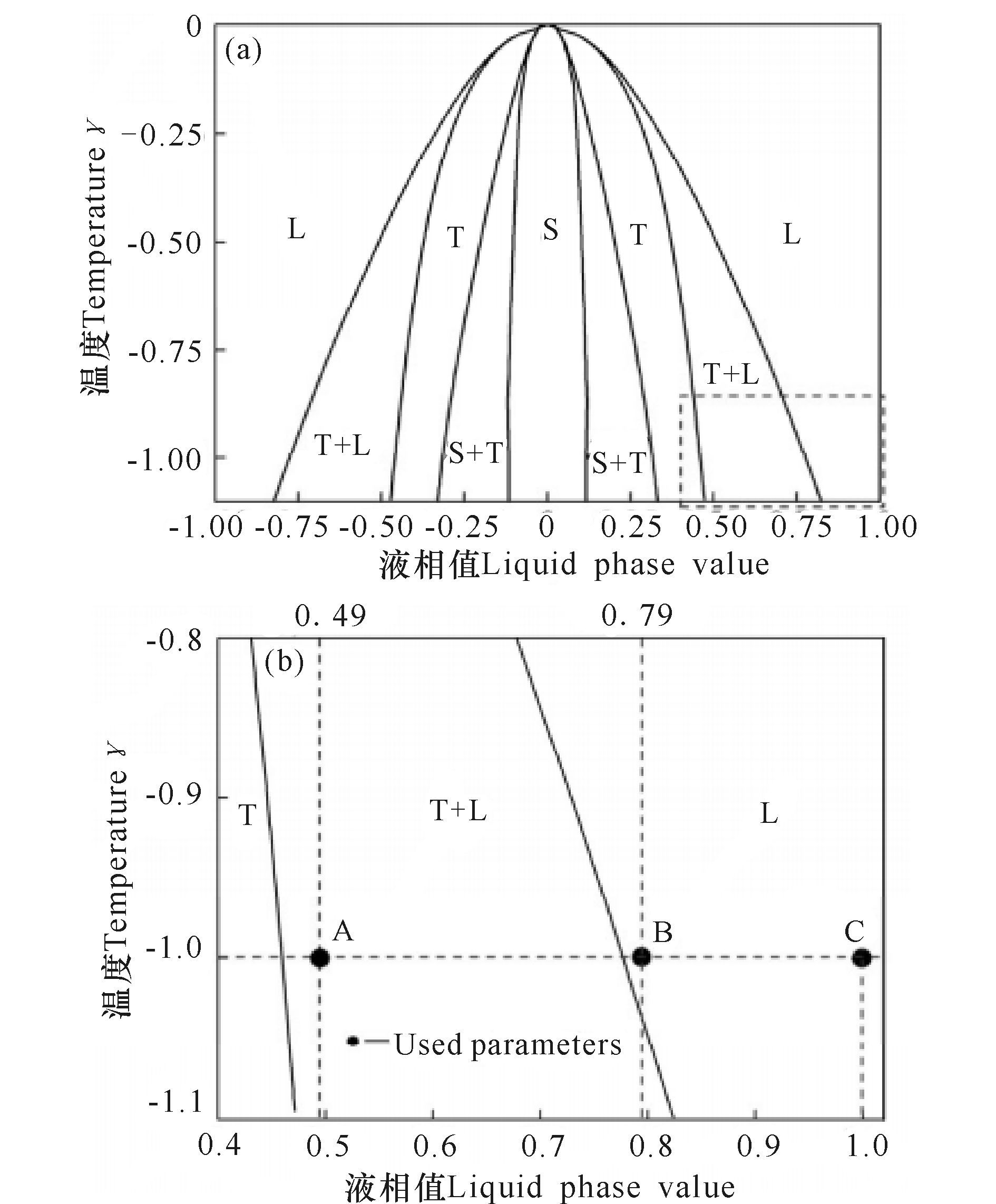
式中,ρ0和γ为体系能量函数的两个重要参数。由体系的能量密度函数可以计算并画出体系的相图。对于二维体系,相区有均匀无序相和晶体相,且晶体相又有六角格子相和条状相两种。文献[6]已给出均匀相和条状相的能量密度函数表达式,按照平衡相图的计算方法可得到二维PFC相图如图 1所示。
|
S、T、L分别表示条状相、三角相、液相;图(b)为图(a)中虚线框的放大图 S, T and L represent stripe phase,triangular phase and liquid phase,respectively;(b)is enlarged image of the dashed box of (a) 图 1 PFC模型的二维相图[6] Fig.1 Two-dimensional phase diagrams of PFC model[6] |
保守的原子密度场变量的演化可用与时间相关的Cahn-Hilliard动力学方程[6]描述
| $\frac{\partial \rho }{\partial t}={{\nabla }^{2}}\frac{\delta F}{\delta \rho }={{\nabla }^{2}}[\gamma \rho +{{\rho }^{3}}+{{(1+{{\nabla }^{2}})}^{2}}\rho ].$ | (5) |
该动力学方程是六阶非线性高阶偏微分方程,在坐标空间求解十分复杂和繁琐。因此,为了提高求解动力学方程(5) 的效率,需要转换到波矢空间求解。这里采用半隐式傅里叶法[6, 17]求解,对式(5) 变换到傅里叶空间[18],整理可得
| ${{{\bar{\rho }}}_{k,t+\Delta t}}=\frac{{{{\bar{\rho }}}_{k,t}}-{{k}^{2}}\Delta t({{{\bar{\rho }}}_{k,{{t}^{3}}}})}{1+{{k}^{2}}\Delta t[r+{{(1+{{k}^{2}})}^{2}}]},$ | (6) |
式中:${\bar{\rho }}$k,t+Δt和${\bar{\rho }}$k,t分别为t+Δt和t时,原子密度ρ在傅里叶空间的变换形式。
1.3 拉伸应变的施加以及参数设置对样品采用等应变(等位移)单轴拉伸加载。在受到拉伸作用后,样品中所有格点的坐标位置都会发生相应的变化。因此,通过格点坐标位置的变化来反映应变作用所引起的样品变形。设变形前的样品中格点位置的坐标用(x,y)表示,施加等应变作用引起变形后,格点位置的坐标用(x′,y′)表示。样品在y方向受到应变εy的拉伸作用。变形前后坐标变换关系为x′=x和y′=y/(1+εy)。由于等应变作用引起样品变形,其内部原子密度函数变为ρ(x′,y′)=ρ(x,y/(1+εy)),因此,在考虑等应变作用引起变形的情况下,原子密度函数表达式(4) 将变换为ρ(x′,y′),体系的能量也随之发生相应的变化,但控制演化的动力学方程的形式保持不变。将样品变形后的原子密度ρ(x′,y′)代入动力学方程(5) 中,采用半隐式傅里叶变换方法整理得到(6) ,对其求解并进行可视化处理,即可得到裂纹扩展的演化图。
本研究模拟不涉及具体材料的物性参数,所用参数均已无量纲化处理,并将连续空间离散为四方格子网格,采用周期性边界条件。计算网格为512Δx×512Δy,空间步长Δx=Δy=π/3,时间步长Δt=0.05。根据单模近似下的二维相图(图 1),本研究选用无量纲密度为ρ0=0.49的三角相表征晶体相,对应的温度参量取为γ=-1.0,如图 1b中A点所示。为模拟中心裂纹,在样品中心设置一定大小的缺口作为初始裂口,其参数设置为ρ0=0.79,γ=-1.0,如图 1b中B点所示。之所以选取该点是因为其对应液相与三角相共存区域附近的原子密度,有利于三角相向裂纹结构转变。原子排列取向角θ=1°。
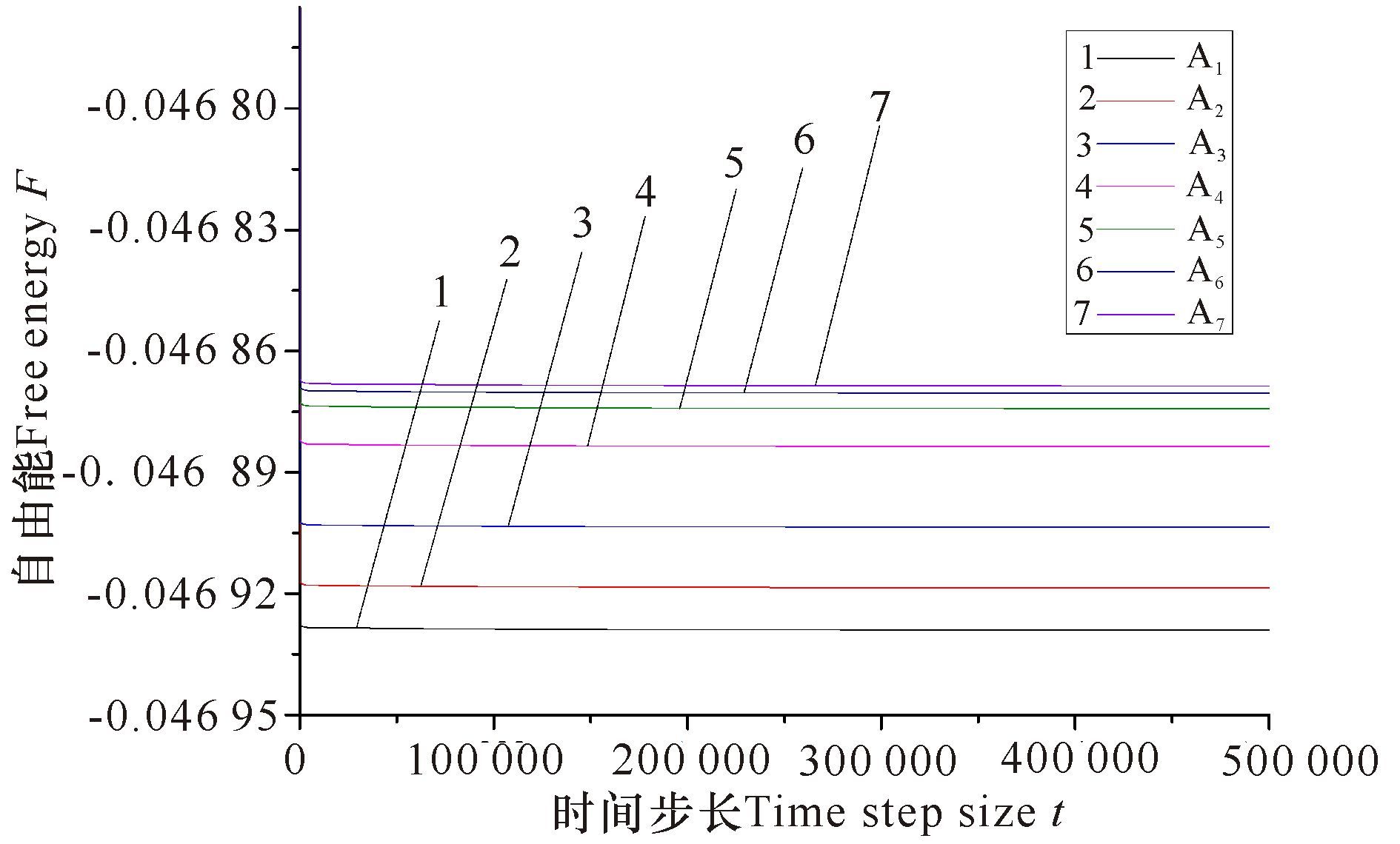
2 结果与分析 2.1 缺口x方向起裂的临界尺寸在施加相同应变情况下,不同的初始缺口尺寸会影响裂纹的萌生与扩展。如图 2所示,本研究施加拉应变方向为单x方向,应变量为ε=10%。固定缺口y方向长度为10个格子,改变缺口x方向的尺寸,分别取10,12,14,16,18,20,22个格子(如表 1样品Ai所示)。图 3a~d为实验条件下,样品A6缺口形貌图,从图 3可以看出,整个过程中初始缺口没有起裂。图 4给出了不同尺寸初始缺口样品的自由能曲线。由于采取恒应变施加的方法,从该图中可观察到,在整个过程,自由能曲线呈水平直线,体系能量保持常量,这表明裂纹没有起裂。由此可以推断,缺口y方向长度固定且较小时,改变缺口x方向的尺寸,不产生缺口起裂;但是随着x方向尺寸的增大,同等应变作用下,整个体系的自由能升高。
|
图 2 施加单轴拉伸应变的示意图 Fig.2 Effect diagram of single biaxial stress |

|
t表示时间步长 t is time step size 图 3 样品A6缺口形貌 Fig.3 The morphology of crack of sample A6 |
|
图 4 样品Ai体系的自由能变化曲线 Fig.4 Free energy change curve of the evolution of sample Ai |
| 表 1 样品参数及起裂情况 Table 1 Sample parameters and crack initiation |
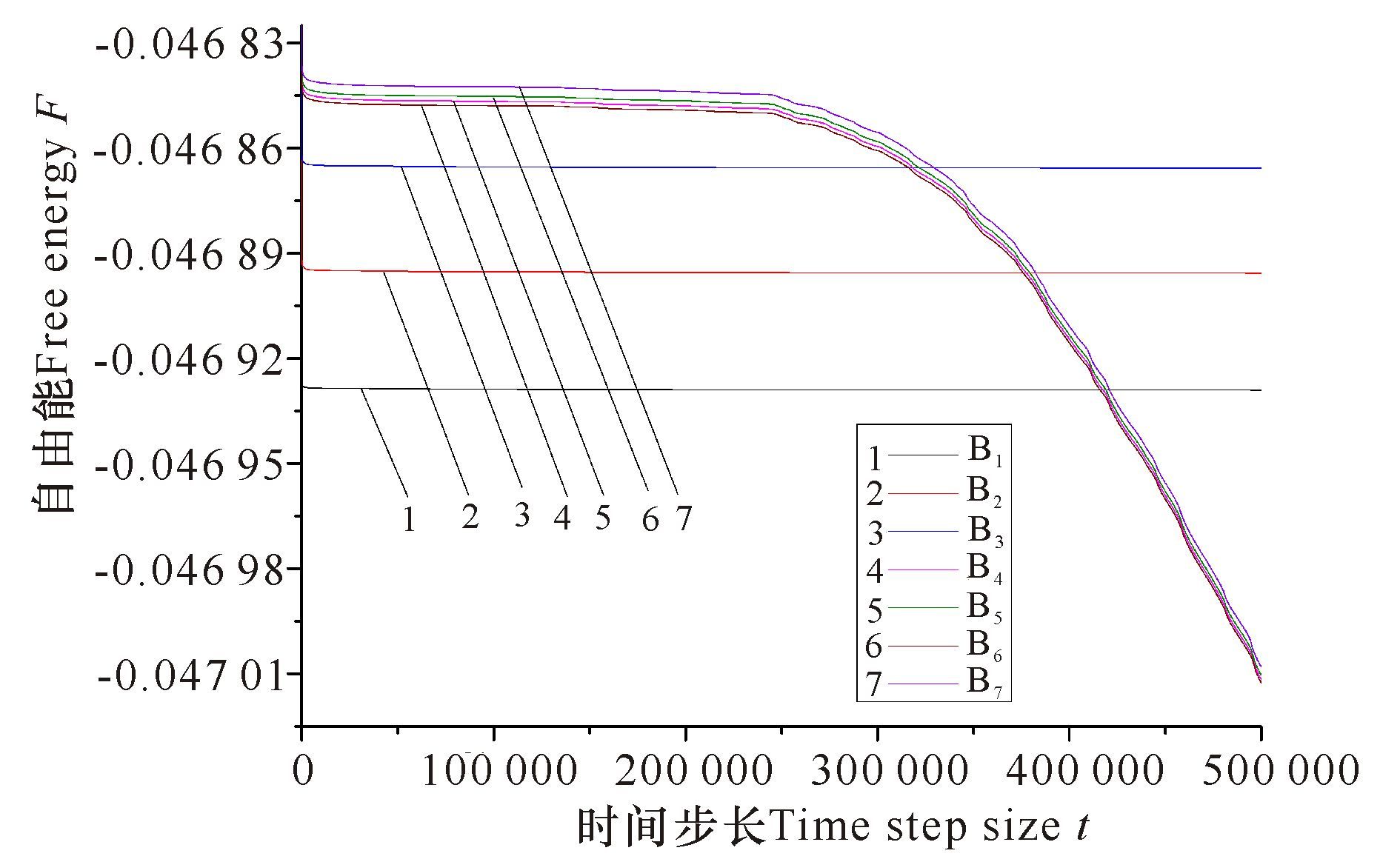
固定缺口x方向尺寸为10个格子,改变初始缺口y方向的尺寸,分别取10,12,14,16,18,20,22个格子(如表 1样品Bi所示)。图 5给出了不同尺寸缺口样品的自由能曲线,从图中可以观察到,当y方向缺口尺寸小于等于14个格子时,自由能几乎是一条水平的直线,反映了整个体系能量基本没有变化,也表明缺口没有起裂。但随着y方向缺口尺寸增大,不同样品能量升高;当y方向尺寸大于14个格子时,自由能曲线在时间步长大约为25万的时候开始降低,这意味着缺口在该时刻开始起裂,体系自由能得到释放。对于y方向缺口尺寸不同的起裂样品,起裂时间与曲线降低速率变化相一致。图 6为样品B6在x方向的应变10%作用下的裂口起裂扩展演化图。从图 6a~b中能看出,缺口没有发生明显的变化,图 6c中缺口出现明显的细小裂缝,对应图 4自由能曲线能量开始降低的时刻,说明缺口已经开始起裂,是由于起裂扩展过程中释放应变能,导致自由能曲线降低。图 7显示了样品B1~B7在时间步长40万步时的裂纹形貌,图 7a~c缺口随着选取缺口参数的不同而有细微的变化,但无明显起裂情况,符合图 4中自由能曲线1,2和3对应的能量变化规律;图 7d~g这4个形貌图中,裂纹的形貌基本一致,符合图 4中自由能曲线4,5,6和7对应的能量变化规律。该结果与格里菲斯强度理论[19]基本一致,即裂纹扩展的应变大小与垂直应变作用方向的缺口尺寸密切相关[20]。
|
图 5 样品Bi裂纹演化过程的体系自由能曲线 Fig.5 Free energy curve of sample Bi |

|
t表示时间步长 t is time step size 图 6 x方向应变10%作用下样品B6的裂纹扩展演化 Fig.6 The morphology evolution of crack propagation of sample B6 under 10% of strain at x direction |

|
图 7 时间步长40万步时样品B1~B7的裂纹形貌 Fig.7 The morphology of the sample B1~B7 at the time step of 400 thousands |
由2.1,2.2的结果可推断,在单x方向施加固定的应变量作用下,裂纹扩展主要是受初始缺口y方向尺寸变化的影响。只有y方向缺口尺寸达到临界值,缺口才会起裂。
2.3 缺口y方向临界尺寸与起裂的关系设置初始缺口y方向尺寸为14个格子,x方向尺寸分别取10,12,14,16,18,20,22个格子(如表 1样品Ci所示),研究在单x方向施加固定的应变量作用下,缺口x方向尺寸变化是否对样品裂纹扩展情况产生影响。图 8给出了不同x方向尺寸样品裂纹演化的自由能曲线。从图中可以观察到,当x方向尺寸取10个格子时,曲线是一条比较平滑的直线,这意味着整个样品体系的能量几乎没有变化,裂纹没有起裂;当x方向尺寸取大于10个格子时,自由能曲线均有明显的下滑过程,能量显著降低,但曲线走向并不是在同一时刻开始降低,这表明不同的x尺寸对应的能量开始降低的起始步长不同。随着缺口x方向尺寸增大,能量降低时间不断延缓,缺口起裂时间不断滞后。由此可知,当缺口y方向尺寸达到裂纹扩展临界尺寸值时,x方向尺寸增加,会延缓缺口的起裂。

|
图 8 样品Ci裂纹演化过程的体系自由能曲线 Fig.8 Free energy curve of evolution of crack propagation of sample Ci |
从图 9中可以看出,当时间步长t达到15万步(图 9b)时,初始缺口还没有出现明显的扩展,缺口边缘已经出现了原子层局部滑移。当时间步长t达到25万步(图 9c)时,缺口已经出现了明显的裂纹扩展,并且随着时间步长的增加,裂纹扩展越明显。图 10显示了样品C1~C7在时间步长40万步时的形貌,图 10a对应图 8中的自由能曲线1,整个过程初始裂口没有起裂;图 10b和图 10c中样品的裂纹形态基本一致,分别对应图 8中的自由能曲线2和3;图 10d~f中3个样品的裂纹形态一致,但是不同于图 10b~c样品裂纹扩展情况,图 10d,10e和10f中的样品分别对应图 8中的自由能曲线4,5和6;图 10g裂纹扩展情况落后于图 10其他已经起裂样品,与图 8中其对应的自由能曲线7降低的拐点落后于其他自由能曲线的情况相符。由此可推断,在施加单方向恒应变及缺口y方向尺寸达到裂纹扩展临界尺寸值的条件下,x方向尺寸改变量较小时,裂纹并不起裂;当增大到临界值时,缺口开始起裂并扩展。

|
图 9 单x方向10%应变作用下样品C6的裂纹扩展演化 Fig.9 The morphology evolution of crack propagation of sample C6 under 10% of strain in uniaxial x direction |

|
图 10 时间步长为40万步时样品C1~C7的形貌 Fig.10 The morphology of the sample C1~C7 at the time step of 400 thousands |
在沿x方向施加恒定10%应变量条件下,缺口y方向尺寸远小于临界值时,改变缺口x方向尺寸并使其增大,缺口不起裂;固定缺口x方向尺寸,改变缺口y方向尺寸并使其增大,当缺口y方向尺寸增大到临界值时,开始起裂并扩展;当缺口y方向尺寸接近临界值时,则改变缺口x方向尺寸时,当x方向尺寸较小时,裂纹并不起裂,随着x增大,当达到x尺寸临界值时,缺口开始起裂并扩展。表明在施加恒应变作用下,缺口起裂与应力作用方向垂直的缺口尺寸密切相关,只有与应变作用方向垂直的尺寸达到临界值,缺口才会发生起裂。
| [1] |
衣林, 陈跃良, 徐丽, 等. 金属材料疲劳微裂纹的萌生与扩展研究[J]. 飞机设计, 2012, 32(2): 63-67. YI L, CHEN Y L, XU L, et al. Research on initiation and propagation of fatigue micro-crack for metal materials[J]. Aircraft Design, 2012, 32(2): 63-67. |
| [2] |
钟群鹏, 周煜, 张峥. 裂纹学[M]. 北京: 高等教育出版社, 2015. ZHONG Q P, ZHOU Y, ZHANG Z. Crack Science[M]. Beijing: Higher Education Press, 2015. |
| [3] |
高英俊, 罗志荣, 黄礼琳, 等. 韧性材料的微裂纹扩展和连通的晶体相场模拟[J]. 中国有色金属学报, 2013, 23(07): 1892-1899. GAO Y J, LUO Z R, HUANG L L, et al. Phase field crastal modeling for microcrack propagation and connecting of ductile materials[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(07): 1892-1899. |
| [4] |
刘晓波, 徐庆军, 刘剑. 铝裂纹扩展行为的分子动力学模拟[J]. 中国有色金属学报, 2014, 24(6): 08. LIU X B, XU Q B, LIU J. Molecular dynamics simulation of crack propagation behavior of aluminum[J]. The Chinese Journal of Nonferrous Metals, 2014, 24(6): 08. |
| [5] |
ELDER K R, KATAKOWSKI M, HAATAJA M, et al. Modeling elasticity in crystal growth[J]. Physical Review Letters, 2002, 88(24): 245701. DOI:10.1103/PhysRevLett.88.245701 |
| [6] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5Pt1): 051605. |
| [7] |
ELDER K R, PROVATAS N, BERRY J, et al. Phase-field crystal modeling and classical density functional theory of freezing[J]. Physical Review B, 2007, 75(6): 064107. DOI:10.1103/PhysRevB.75.064107 |
| [8] |
BERRY J, GRANT M, ELDER K R. Diffusive atomistic dynamics of edge dislocations in two dimensions[J]. Physical Review E, 2006, 73(3Pt1): 031609. |
| [9] |
杨涛, 陈铮, 董卫平. 应力诱发双位错组亚晶界湮没的晶体相场模拟[J]. 金属学报, 2011, 47(10): 1301-1306. YANG T, CHEN Z, DONG W P, et al. Phase field crystal simulation of stress-induced annihilation of sub-grain boundary with double-array dislocation[J]. Acta Metallurgica Sinica, 2011, 47(10): 1301-1306. |
| [10] |
罗志荣, 黄世叶, 茹谢辛, 等. 晶体相场法模拟大角度晶界的变形过程[J]. 广西科学, 2013, 20(4): 311-315. LUO Z R, HUANG S Y, RU X X, et al. Phase-field-crystal modeling for deformation process of high-angle grain boundary[J]. Guangxi Sciences, 2013, 20(4): 311-315. |
| [11] |
高英俊, 罗志荣, 黄创高, 等. 晶体相场方法研究二维六角相向正方相结构转变[J]. 物理学报, 2013, 62(5): 050507-050510. GAO Y J, LUO Z R, HUANG C G, et al. Phase-field-crystal modeling for two-dimensional transformation from hexagonal to square structure[J]. Acta Physica Sinica, 2013, 62(5): 050507. |
| [12] |
YU Y M, BACKOFEN R, VOIGT A. Morphological instability of heteroepitaxial growth on vicinal substrates:A phase-field crystal study[J]. Journal of Crystal Growth, 2011, 318(1): 18-22. DOI:10.1016/j.jcrysgro.2010.08.047 |
| [13] |
高英俊, 王江帆, 罗志荣, 等. 晶体相场方法模拟纳米孪晶结构[J]. 计算物理, 2013, 30(4): 577-581. GAO Y J, WANG J F, LUO Z R, et al. Nano-twin structure simulation with phase field crystal method[J]. Chinese Journal of Computational Physics, 2013, 30(4): 577-581. |
| [14] |
HU S, CHEN Z, PENG Y Y, et al. Modeling and simulation of microcrack propagation behavior under shear stress using phase-field-crystal[J]. Computational Materials Science, 2016, 121: 143-150. DOI:10.1016/j.commatsci.2016.04.035 |
| [15] |
GOMEZ H, NOGUEIRA X. An unconditionally energy-stable method for the phase field crystal equation[J]. Computer Methods in Applied Mechanics and Engineering, 2012, 249-252: 52-61. DOI:10.1016/j.cma.2012.03.002 |
| [16] |
ELDER K R, ROSSI G, KANERVA P, et al. Patterning of heteroepitaxial overlayers from nano to micron scales[J]. Physical Review Letters, 2012, 108(22): 226102. DOI:10.1103/PhysRevLett.108.226102 |
| [17] |
卢成健, 蒋丽婷, 王玉玲, 等. 晶体相场法模拟小角度晶界的位错结构及其演化[J]. 广西科学, 2013, 20(4): 316-320. LU C J, JIANG L T, WANG Y L, et al. Dislocation structure evolution in low angle grain boundary[J]. Guangxi Sciences, 2013, 20(4): 316-320. |
| [18] |
毛鸿, 罗志荣, 黄世叶, 等. 材料裂纹扩展分叉机理的晶体相场法研究[J]. 广西科学, 2015(5): 499-505. MAO H, LUO Z R, HUANG S Y, et al. Phase-field-crystal modeling for crack propagation and branch of materials[J]. Guangxi Sciences, 2015(5): 499-505. |
| [19] |
张俊善. 材料强度学[M]. 黑龙江: 哈尔滨工业大学出版社, 2004. ZHANG S J. Strength of Materials[M]. Heilongjiang: Harbin Institute of Technology Press, 2004. |
| [20] |
师俊平, 胡义锋, 罗峰. 裂纹起裂方向及扩展路径的数值模拟[J]. 力学季刊, 2013, 34(02): 233-239. SHI J P, HU Y F, LUO F. Numerical simulation of crack initiation directions and its propagation path[J]. Chinese Quarterly of Mechanics, 2013, 34(2): 233-239. |
 2016, Vol. 23
2016, Vol. 23 


