【研究意义】材料内部的微观缺陷决定材料的宏观性能[1-2]。微观缺陷包括位错、空位、晶界、空洞和微裂纹等。通常这些微观缺陷是在纳米尺度上发生非平衡复杂动力学过程中生成[3]。金属材料的变形加工与材料的位错等微观缺陷运动有密切关系。在目前条件下,材料的原子尺度结构的演化很难被实验原位观测到。因此,计算机模拟实验已成为精确揭示这些微观缺陷运动的重要方法和实验补充[4]。【前人研究进展】相场法是当今研究微观缺陷结构演化的有效计算工具[5-6]。传统相场法[7-8] 建立在平衡态均匀场基础上,该方法忽略了原子周期排列结构所产生的物理特性,因此难以反映晶体周期结构特性以及纳观尺度的缺陷行为,也无法从根本上揭示微观结构运动过程中的动力学机理。最近,基于泛函密度理论的晶体相场(Phase-field-crystal,PFC)模型[9-11]引入周期性局域密度场作为序参量,将晶相的密度场表示成周期性函数形式,进而通过该密度函数反映晶体的周期结构。该密度场很自然地与晶粒取向和位错的运动、弹性效应等物理特性自洽地联系起来[10]。现在,PFC模型已成功模拟了位错攀移、滑移和亚晶界湮没[11-12]、晶界位错预熔化[13]、异质外延生长[14]、晶体结构的相转变[15]、韧性材料的微裂纹扩展与连通[16]、纳米晶界结构设计[17]等。【本研究切入点】到目前为止,应用PFC模型详细研究双位错运动还未见报道。【拟解决的关键问题】应用改进PFC模型[18]研究晶体的双位错在剪应变作用下的滑移特征,揭示剪切应变作用对位错滑移的影响。
1 PFC模型与方法 1.1 体系的自由能密度函数按照文献[10]的做法,用原子密度函数表示相场变量,其表达式可写成
| $\rho \left( r \right)=\sum\limits_{n,m}{{{a}_{n,m}}}{{e}^{\overrightarrow{iG}\cdot \vec{r}}}+{{\rho }_{0}},$ | (1) |
式中,等号右边第一项是原子的周期排列特征项,第二项是液相的原子无规项。参考文献[19]的思想和方法,本文在原始的PFC模型基础上,加入体系原子密度与外力场耦合的作用项,则体系无量纲的自由能函数可以写成
| $F=\int{\left\{ \frac{\rho }{2}\left[ \gamma +{{(1+{{\nabla }^{2}})}^{2}} \right]\rho +\frac{{{\rho }^{4}}}{4}+{{V}_{ext}}\cdot \rho \right\}}dr,$ | (2) |
式中,r为温度参量,∇2为Laplace算子;Vext·ρ为外加力场与样品原子密度函数的耦合作用,Vext为外力场,其具体的数学表达式见文献[18]。该改进的自由能模型自洽地包含了晶体周期物理特征。
平衡时的三角晶体相的原子密度函数ρ可写成单模形式
| $\rho \left( x,y \right)={{A}_{0}}[cos\text{ }\left( qx \right)cos\text{ }\left( \frac{qy}{\sqrt{3}} \right)\text{ }-\frac{1}{2}cos\text{ }\left( \frac{2qy}{\sqrt{3}} \right)\text{ }]+{{\rho }_{0}},$ | (3) |
式中,A0是固相原子密度的振幅;ρ0为液相的原子密度平均值。将式(4) 代入式(2) ,对A0和q分别求导数,得到A0的表达式为
| ${{A}_{0}}=\frac{4}{5}({{\rho }_{0}}+\frac{1}{3}\sqrt{-15r-36{{\rho }_{0}}^{2}}),$ | (4) |
由体系的极小自由能密度函数可以得到二维体系不同相区的相图。按照计算相图的方法[10]得到的二维相图如图 1所示。

|
L:液相区;S:条状相区;T:六角结构相区 L:Liquid phase;S:Stripe phase;T:Triangular phase 图 1 二维PFC相图 Fig.1 2D PFC phase diagram |
由于原子密度场ρ为保守场,所以演化的无量纲动力学方程满足Chan-Hilliard方程[14]
| $\frac{\partial \rho }{\partial t}={{\nabla }^{2}}\frac{\delta F}{\delta \rho }={{\nabla }^{2}}[(r+{{(1+{{\nabla }^{2}})}^{2}})\rho +{{\rho }^{3}}+{{V}_{ext}}],$ | (5) |
为求解复杂的动力学方程式(5) ,还必须将动力学方程在时间和空间进行离散化处理,即采用数值求解的办法。在本文的数值求解中,采用显型Euler迭代公式[8]
| $\rho \left( t+\Delta t \right)=\rho \left( t \right)+\frac{d\rho }{dt}\cdot \Delta t,$ | (6) |
式中,Δt为离散时间步长。此外,为使数值解具有稳定性,需将Laplace算子作用考虑到次近邻格点[8]
| ${{\nabla }^{2}}{{\rho }_{i}}=\frac{1}{{{\left( \Delta x \right)}^{2}}}\frac{1}{2}\left[ \sum\limits_{j}{({{\rho }_{j}}-{{\rho }_{i}})}+\frac{1}{4}\sum\limits_{n}{({{\rho }_{j}}-{{\rho }_{i}})} \right],$ | (7) |
式中,Δx为离散空间步长,j和n分别代表i的最近邻格点与次近邻格点。利用可视化函数imshow出原子密度函数ρ(x,y)分布图。
1.3 样品制备为方便起见,以FCC面心立方晶格的{111}平面作为模拟实验的结构体系。要在等效于{111}平面的二维六角原子晶格点阵中产生一对孤立的刃位错,可以利用六角结构的原子密度分布函数公式(4) 来设置。在模拟区域上设置为双晶结构,晶界的取向差设为θ=0.65°。二个位错位于晶界上,该体系为双晶结构,且晶界上各有一个孤立位错,形成位错对(如图 2红色的位错符号所示)。对于设定的r值,与之相应的ρ0取值如图 1所示,取在液固两相共存的边界上。本研究详细的模拟参数如下:模拟区域设置为256⊿x*256⊿y,单元格子⊿x=⊿y=0.75,时间步长t=0.5,样品弛豫时间步数n=50 000;固相区的参数为(ρ0,r)=(0.364 2,-0.45) ,液相区的参数为(ρ0,r)=(0.469 5,-0.45) ,得到的具有晶界位错的样品如图 2a所示。
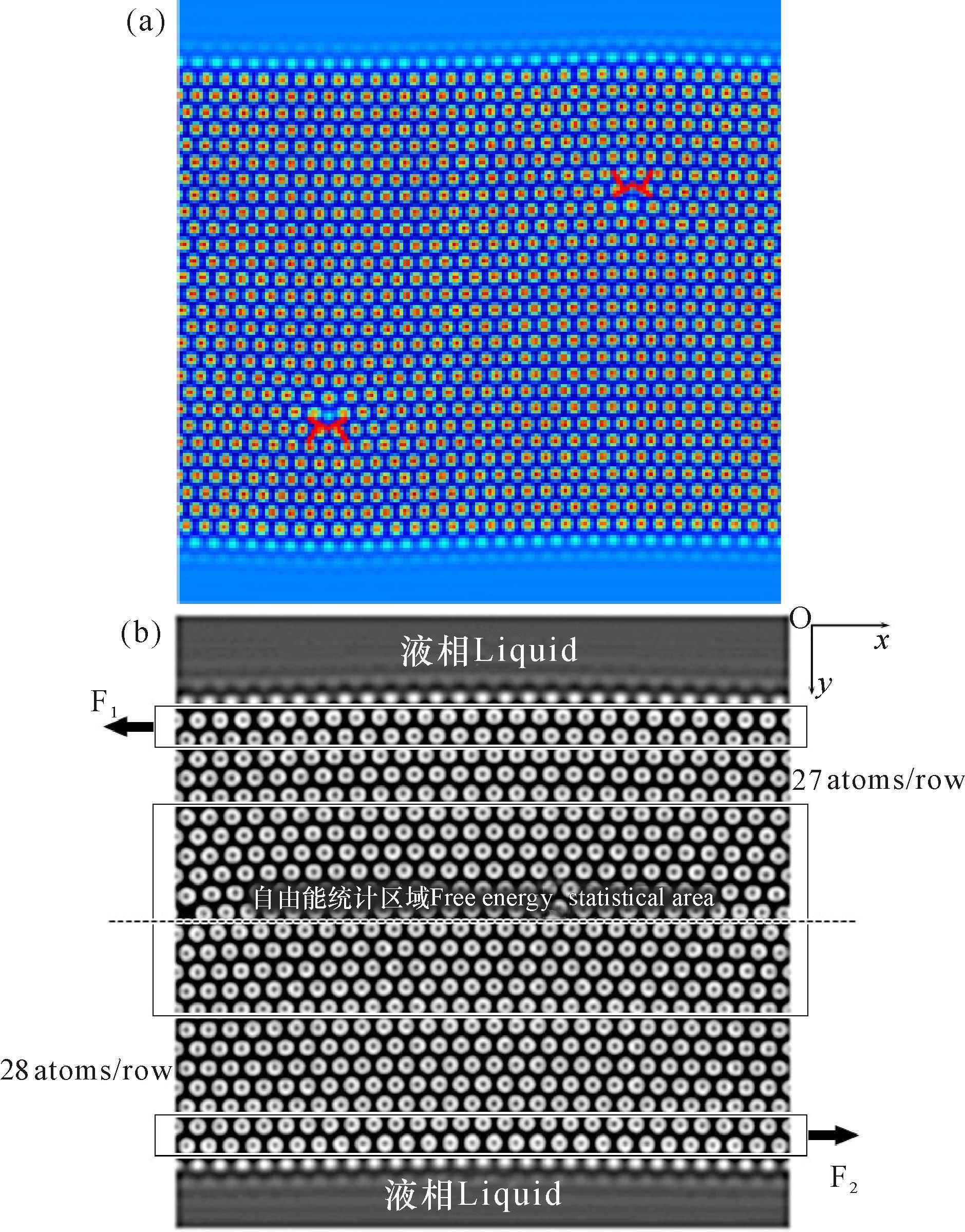
|
F1和F2为剪切应力,F1=-F2 F1 and F2 are the shear strain,F1=-F2 图 2 样品(a)及施加剪切应变的示意图(b) Fig.2 The sample (a) and exerting shear strain diagram (b) |
PFC方法在固相与自由表面之间设置液相区域与之衔接[10],这样就可以模拟晶粒在剪切应力作用下的位错运动情况。图 2b中给出了本模型施加剪切应变的示意图。本研究采用文献[19]给出的外力场的耦合方式,就可做到位错周围的原子克服Peierls势,实现位错攀移和滑移运动。
在模拟刃型位错运动时,对图 2的样品两侧应用周期性边界条件。如图 2b所示,x轴位于样品的中心沿水平方向,样品分成上下两半,设置靠近上下两端液相区的晶粒最外两原子层为耦合外力场区域,施加的周期外力场用Vext(x,y)表示,具体施加的上下外力场分别用V+(x,y)和V-(x,y)表示(参考文献[9]给出了剪切应变的外力场形式)。本文计算时设A=1;作用力V+(x,y)为沿正x方向,作用在晶粒上半部顶层的二层原子上,而作用力V-(x,y)为沿负x方向,作用在晶粒下半部底层的二层原子侧面上;外力场施加作用时,每进行n个时间步的应变作用,则让原子晶格弛豫运动,于是剪切应变逐渐传递到样品中部的位错原子周围。由于外力场的函数形式与密度场的函数形式相似,因此,两者可以产生耦合作用。由于体系原子跟随着外力场进行耦合运动,于是产生了施加剪切应变的物理效果。本文将施加的应变率设定在中间速应变率范围,如=(3.33×10-3~5.0×10-2)/t,其中,时间t为无量纲。本研究采用的应变率与实际符合。
2 结果与分析应用公式(5) ~(7) ,可以计算位错的运动演化过程。利用公式(2) ,可以计算体系自由能随位错运动的变化情况。图 3为不同的应变率作用下,样品中位错的滑移运动的位置随时间的变化,其中位错1的x和y的坐标位于图的左边坐标,用蓝色和绿色表示,位错2的x和y的坐标位于图的右边坐标,用粉红色和金黄色表示。当施加的应变率较大(=5.0×10-2/Δt)时,样品中二个位错都发生沿x方向的运动,但方向相反,而在y方向没有移动(图 3a)。由此可见,这二个位错只作滑移运动,没有攀移运动。当应变率较小(=2.0×10-2/Δt、1.0×10-2/Δt、6.7×10-3/Δt和5.0×10-3/Δt)时,位错只滑移运动,没有攀移运动,施加的应变率越小,位错滑移走过的距离越短(图 3b~c)。当施加的应变率小于=4.0×10-3/Δt时,位错静止,这二个位错位置保持不变(图 3e),表明位错没有发生滑移运动。这说明=4.0×10-3/Δt是位错发生滑移运动的临界应变率。此外,这二个位错运动方向平行且相反,由于不发生位错攀移,因此不出现位错滑移交叉现象。由图 3还可见,在较大时,位错的滑移运动保持匀速运动,当=5.0×10-2/Δt时,位错滑移速度近似为v=4.44格/(100 ts),当=2.0×10-2/Δt时,位错滑移速度近似为v=2.0格/(100 ts);在较小时,滑移出现颠簸运动特征,位错位移曲线出现较大的台阶特征(图 3d~e)。
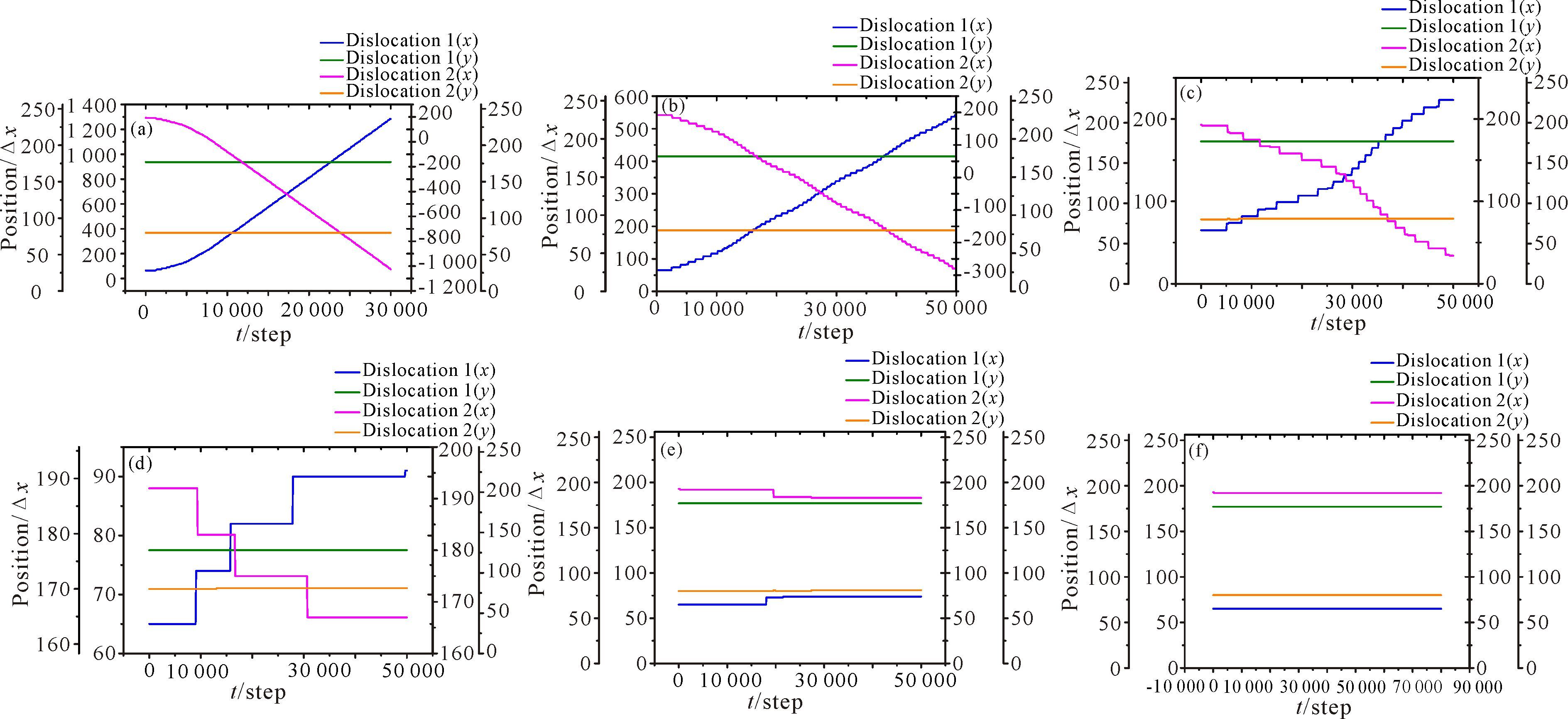
|
(a)=5.0×10-2/Δt;(b)=2.0×10-2/Δt;(c) =1.0×10-2/Δt;(d)=6.7×10-3/Δt;(e)=5.0×10-3/Δt;(f)=4.0×10-3/Δt 图 3 样品在不同的剪切应变作用下位错位置随时间变化的曲线 Fig.3 Samples at different shear strain under the dislocation position changes over time |
图 4给出了位错滑移运动过程中位错区域周围的能量变化。由图 4可见,这二个位错运动引起能量的变化规律是明显不同的。当应变率较大时,在开始阶段,体系自由能是单调增加的,在自由能曲线前端会出现一个峰,然后趋于平缓(图 4a),表明位错滑移越过临界势垒后,滑移进入平稳运动阶段,这对应于位错作匀速直线运动。由图 4b可见,整个自由能曲线呈现3个宽的峰和谷特征,在曲线中还存在许多小的峰谷结构,这是位错翻过原子势垒而引起的;而大的峰谷结构是由于双位错滑移运动引起液固界面波动弛豫造成的。图 4c与图 4b有类似现象,但只存在一个大的峰和谷,以及多个小峰谷。由图 4d~f可见,自由能曲线是单调增加的,且出现若干孤立的峰,这表明在应变率较小的情况下,位错滑移运动过程越过势垒需要一定孕育时间,因此,出现颠簸式的运动特征。这在较大的应变率作用下并不出现。在本研究条件下,没有观察到位错攀移运动,是因为本模型实验的温度参数较小,温度较低,原子晶格结合能较强,位错无法克服原子键阻力势垒,故位错不出现攀移现象。当温度参数增加,原子键相互作用力减弱,位错就可以出现攀移和滑移同时进行,文献[20]已有这方面的报道。
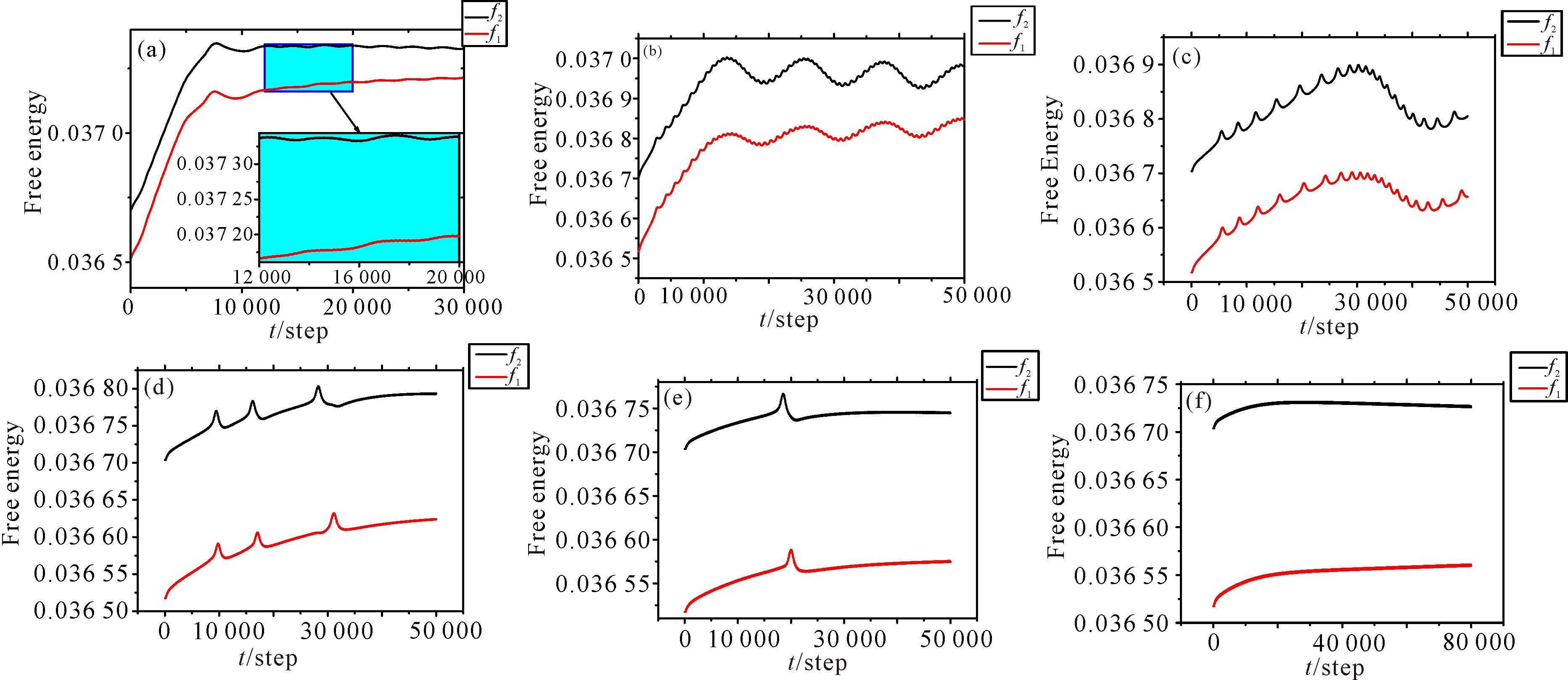
|
(a)=5.0×10-2/Δt;(b)=2.0×10-2/Δt;(c)=1.0×10-2/Δt;(d)=6.7×10-3/Δt;(e)=5.0×10-3/Δt;(f)=4.0×10-3/Δt 图 4 体系在不同剪切应变作用下的自由能曲线 Fig.4 Free energy of the system under the effect of different shear strain |
PFC模型能较好地用于研究位错在应变作用下的运动。在温度较低的条件下施加应变作用,当应变率较大时,体系的双位错只作滑移运动,运动方向平行且相反,保持匀速运动,不出现攀移运动;当应变率较小时,位错滑移运动过程越过势垒需要一定孕育时间,此时滑移出现颠簸式运动特征。这些结果与实验结果相符合。
| [1] |
徐恒均, 刘国勋. 材料科学基础[M]. 北京: 北京工业出版社, 2001: 265-279. XU H J, LIU G X. Fundamentals of Materials Science[M]. Beijing: Beijing Industry Press, 2001: 265-279. |
| [2] |
胡赓祥, 蔡珣, 戎咏华. 材料科学基础[M]. 3版. 上海: 上海交通大学出版社, 2010: 265-279. HU G X, CAI X, RONG Y H. Fundamentals of Materials Science[M]. 3rd edition. Shanghai: Shanghai Jiao Tong University Press, 2010: 265-279. |
| [3] |
BOBYLEV S V, OVID'KO I A. Transformations of faceted grain boundaries in high-Tc superconductors[J]. Physical Review B, 2003, 67(13): 132506. DOI:10.1103/PhysRevB.67.132506 |
| [4] |
OVID'KO I A, SKIBA N V. Enhanced dislocation emission from grain boundaries in nanocrystalline materials[J]. Scripta Materialia, 2012, 67(1): 13-16. DOI:10.1016/j.scriptamat.2012.03.007 |
| [5] |
GUTKIN M Y, OVID'KO I A. Transformations of low-angle tilt boundaries in high-Tc superconductors[J]. Physical Review B, 2001, 63(6): 064515. DOI:10.1103/PhysRevB.63.064515 |
| [6] |
张林, 王绍青, 叶恒强. 大角度Cu晶界在升温、急冷条件下晶界结构的分子动力学研究[J]. 物理学报, 2004, 53(8): 2497-2502. ZHANG L, WANG S Q, YE H Q. Molecular dynamics study of the structure changes in a high-angle Cu grain boundary by heating and quenching[J]. Acta Physica Sinica, 2004, 53(8): 2497-2502. |
| [7] |
ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals[J]. Physical Review E, 2004, 70(5): 051605. DOI:10.1103/PhysRevE.70.051605 |
| [8] |
ELDER K R, PROVATAS N, BERRY J, et al. Phasefi-eld crystal modeling and classical density functional theory of freezing[J]. Physical Review B, 2007, 75(6): 064107. DOI:10.1103/PhysRevB.75.064107 |
| [9] |
BERRY J, GRANT M, ELDER K R. Diffusive atomistic dynamics of edge dislocations in two dimensions[J]. Physical Review E, 2006, 73(3): 031609. DOI:10.1103/PhysRevE.73.031609 |
| [10] |
黄世叶, 刘晓骅, 谢森, 等. 剪切应力作用下位错运动的晶体相场模拟[J]. 广西科学, 2015, 22(4): 400-406. HUANG S Y, LIU X H, XIE S, et al. Phase-field-crystal simulation of dislocation gliding under shear strain[J]. Guangxi Sciences, 2015, 22(4): 400-406. |
| [11] |
罗志荣, 黄世叶, 茹谢辛, 等. 晶体相场法模拟大角度晶界的变形过程[J]. 广西科学, 2013, 20(4): 311-315. LUO Z R, HUANG S Y, RU X X, et al. Phase field crystal modeling for deformation process of high-angle grain boundaries[J]. Guangxi Science, 2013, 20(4): 311-315. |
| [12] |
BERRY J, ELDER K R, GRANT M. Melting at dislocations and grain boundaries:A phase field crystal study[J]. Physical Review B, 2008, 77(22): 224114. DOI:10.1103/PhysRevB.77.224114 |
| [13] |
陈成, 陈铮, 张静, 等. 晶体相场法模拟异质外延过程中界面形态演化与晶向倾侧[J]. 物理学报, 2012, 61(10): 108103. CHEN C, CHEN Z, ZHANG J, et al. Simulation of morphological evolution and crystallographic tilt in heteroepitaxial growth using phase-field crystal method[J]. Acta Physica Sinica, 2012, 61(10): 108103. |
| [14] |
YU Y M, BACKOFEN R, VOIGT A. Morphological instability of heteroepitaxial growth on vicinal substrates:A phase-field crystal study[J]. Journal of Crystal Growth, 2011, 318(1): 18-22. DOI:10.1016/j.jcrysgro.2010.08.047 |
| [15] |
ARAFIN M A, SZPUNAR J A. A new understanding of intergranular stress corrosion cracking resistance of pipeline steel through grain boundary character and crystallographic texture studies[J]. Corrosion Science, 2009, 51(1): 119-128. DOI:10.1016/j.corsci.2008.10.006 |
| [16] |
高英俊, 罗志荣, 黄创高, 等. 晶体相场方法研究二维六角相向正方相结构转变[J]. 物理学报, 2013, 62(5): 050507. GAO Y J, LUO Z R, HUANG C G, et al. Phase-field-crystal modeling for two-dimensional transformation from hexagonal to square structure[J]. Acta Physica Sinica, 2013, 62(5): 050507. |
| [17] |
高英俊, 罗志荣, 黄礼琳, 等. 韧性材料的微裂纹扩展和连通的晶体相场模拟[J]. 中国有色金属学报, 2013, 23(7): 1892-1899. GAO Y J, LUO Z R, HUANG L L. Phase-field-crystal modeling for microcrack propagation and connecting of ductile materials[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(7): 1892-1899. |
| [18] |
卢成健, 蒋丽婷, 王玉玲, 等. 晶体相场法模拟小角度晶界的位错结构及其演化[J]. 广西科学, 2013, 20(4): 316-320. LU C J, JIANG L T, WANG Y L, et al. Simulating structure of dislocation and its evolution in low angle grain boundary by phase field crystal method[J]. Guangxi Science, 2013, 20(4): 316-320. |
| [19] |
HIROUCHI T, TAKAKI T, TOMITA Y. Effects of temperature and grain size on phase-field-crystal deformation simulation[J]. International Journal of Mechanical Sciences, 2010, 52(2): 309-319. DOI:10.1016/j.ijmecsci.2009.09.036 |
| [20] |
COLOMBO D, MASSIN P. Fast and robust level set update for 3D non-planar X-FEM crack propagation modelling[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(25/26/27/28): 2160-2180. |
 2016, Vol. 23
2016, Vol. 23 


