2. 广西大学物理科学与工程技术学院,广西 南宁 530004
2. College of Physical Science and Technology,Guangxi University,Nanning,Guangxi,530004,China
【研究意义】多晶材料的晶粒尺寸直接影响材料的强度、塑性、韧性以及耐腐蚀性等性能,因此研究多晶材料晶粒尺寸的演化规律具有重要意义[1-2]。【前人研究进展】近年来,随着材料科学与计算机技术的快速发展,利用计算机模拟研究材料微结构演化过程已成为大趋势。当前,利用计算机模拟晶粒长大的主要模拟方法有蒙特卡洛法(Monte Carlo)[3-5],元胞自动机法(Cellular Automaton)[6-7]以及相场法(Phase Field)[8-12]。在这些模拟方法中,相场法因具有深刻的物理思想,不需要追踪复杂界面的运动等优势而成为强有力的模拟方法。1994年,Chen和Yang[8]构建了单相晶粒长大的相场模型,研究二维晶粒长大过程及晶粒尺寸分布特征。1996年,Chen和Fan[9]构建了两相晶粒长大的相场模型,研究Al2O3-ZrO2两相晶粒长大过程及微结构特征。2001年,Kazaryan等[10]利用相场法研究晶界迁移率各向异性对单相晶粒长大的形貌、动力学和拓扑结构的影响。2002年,Krill和Chen[11]利用相场法研究三维晶粒长大过程及其动力学和拓扑特性。2011年,魏承炀和李赛毅[12]采用相场法研究单相多晶材料退火过程中,由温度梯度引起的非均匀二维晶粒长大和定向晶粒长大行为。【本研究切入点】目前,利用相场法研究初始微结构对晶粒长大过程的影响还鲜有报到。【拟解决的关键问题】采用相场法模拟单相多晶材料中正常晶粒及初态分别为柱状和梯度微结构的晶粒长大过程,从晶粒形貌和晶粒尺寸等方面进行分析讨论,揭示晶粒长大的规律。
1 模型与方法 1.1 相场模型在相场模型中,多晶材料的微结构可用一系列非保守的取向场变量ηi(r,t),(i=1,2,…,p)来表征,其中p为晶粒取向个数。这些场变量是空间r和时间t的连续函数,其值为0~1或-1~0。例如,在第q个取向的晶粒中,ηi=q=1(或-1),ηi≠q=0;在晶界处,ηi在0和1(或0和-1)之间连续变化。材料微观结构演化的驱动力来自系统总自由能的降低。系统总自由能F可表示为[8]
| $F = \int {_V} \left\{ {{f_0}({\eta _1},{\eta _2}, \ldots ,{\eta _p}) + \sum\limits_{i = 1}^p {{k_i}2{{(\nabla {\eta _i})}^2}} } \right\}{d^3}r$ | (1) |
式中,ki为能量梯度系数;f0为自由能密度函数,其表达式为[8]
| ${f_0} = \sum\limits_{i = 1}^p { - \frac{\alpha }{2}\eta _i^2 + \frac{\beta }{4}\eta _i^4 + \frac{\gamma }{2}} \sum\limits_p^{i = 1} {\sum\limits_{j \ne i}^p {\eta _i^2\eta _j^4} } $ | (2) |
式中,α、β和γ为正实数,要求γ>β。
由于取向场变量是非保守场变量,它们随时间的演化由Ginzburg-Landau方程组描述[8]
| $\begin{array}{l} \frac{{\partial {\eta _i}\left( {r,t} \right)}}{{\partial t}} = - {L_i}\frac{{\delta F}}{{\delta {\eta _i}\left( {r,t} \right)}} = - {L_i}( - \alpha {\eta _i} + \beta \eta _i^3 + \\ \gamma {\eta _i}\sum\limits_{j \ne i}^p {\eta _i^2 - {k_i}{\nabla ^2}{\eta _i})} ,i = 1,2, \ldots ,p \end{array}$ | (3) |
式中,Li为晶界迁移率。
为求解动力学方程(3),需要在时间和空间上对其进行离散化处理。在时间上,采用显式Euler迭代公式[8]
| ${\eta _i}\left( {t + \Delta t} \right) = {\eta _i}\left( t \right) + \frac{{{\rm{d}}{\eta _i}\left( t \right)}}{{{\rm{d}}t}}\Delta t$ | (4) |
式中,Δt为时间步长。
在空间上,对式(3)中的Laplace算子采用九点差分格式离散[8]
| $\begin{array}{l} {\nabla ^2}{\eta _i} = \frac{1}{{{{\left( {\Delta x} \right)}^2}}}[\frac{1}{2}\sum\limits_j {({\eta _j} - {\eta _i})} + \frac{1}{4}\sum\limits_n {({\eta _n} - } \\ {\eta _i})] \end{array}$ | (5) |
式中,Δx为空间步长,j
本研究不针对具体材料,所采用的参数均已无量纲化。计算时,将连续空间离散为四方格子,计算区域为512×512 gp(gp表示格子点数)。对于正常晶粒长大,其取向场变量ηi的初始值设置为在[-0.001,0.001]之间的随机数。其他参数设置为p=36,α=β=1.0,γ=2.0,Li=1.0,ki=2.0,Δx=2.0,Δt=0.25。对所有格点遍历处理一次后计为一个模拟时间步(ts),并最终模拟出整个晶粒的长大过程。
2 结果与分析 2.1 正常晶粒长大图 1为晶粒长大过程中不同时刻的晶粒组织,其中不同颜色区域表征不同取向晶粒。可见,随着演化的进行,大晶粒逐渐长大,小晶粒逐渐缩小直至消失,使得晶粒数量减小,平均晶粒尺寸增大。由图 1还可见,在演化初期,晶界较弯曲,曲率较大,边数大于6的晶粒晶界呈现内凹形状,而边数少于6的晶粒具有凸出的特征。随着演化的进行,晶界在向其曲率中心迁移的过程中逐渐趋于平直,三叉晶界夹角趋于120°,与文献[13]的实验观察结果及晶粒长大理论[14]吻合。

|
(a)1×103 ts;(b)6×103 ts;(c)2×104 ts 图 1 正常晶粒长大过程中的晶粒形貌 Fig.1 Grain morphology during normal grain growth |
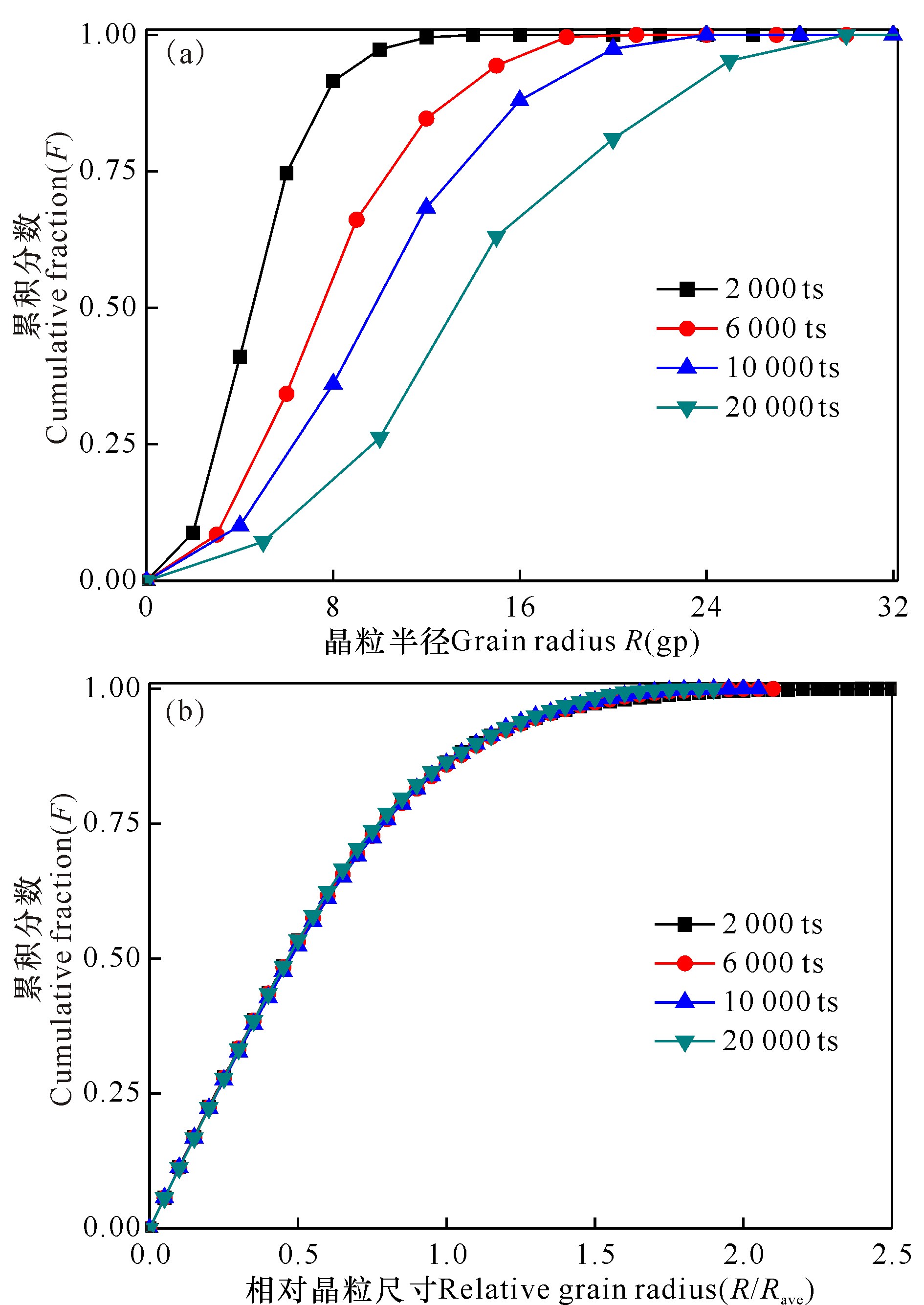
图 2a和b分别为不同演化时间的晶粒尺寸分布和相对晶粒尺寸分布曲线。可见,随着演化时间的增加,晶粒尺寸分布沿大尺寸方向转移(图 2a),而相对晶粒尺寸分布基本保持不变,具有自相似性(图 2b),与文献[15]的实验结果一致。
|
图 2 晶粒长大过程中晶粒尺寸分布(a)和相对晶粒尺寸分布(b) Fig.2 Grain size distribution (a) and relative grain size distribution (b) during grain growth |
为研究多晶长大过程中单个晶粒的尺寸随时间的变化情况,在晶粒演化到500 ts时随机选取9个大小各异的晶粒,并监测其面积(晶粒的格点数量)。图 3为这9个晶粒的面积随时间的变化曲线。可见,随着演化的进行,在演化初期尺寸较小的晶粒,其面积一直减小,并在较短时间内消失;而在演化初期尺寸较大的晶粒,一部分持续长大,另一部分在长大到某一时刻面积开始减小,直至完全消失。这说明小晶粒在演化初期就被周围的大晶粒吞噬,而初始晶粒中尺寸较大的晶粒在长大过程中其相邻晶粒不断发生变化,当其被更大尺寸的晶粒包围时,其面积就会减小,直至晶粒消失。只有在长大过程中一直处于优势地位的大晶粒,才能持续长大。

|
图 3 随机选取的9个不同尺寸晶粒的面积与演化时间的关系 Fig.3 Temporal evolution of the areas of 9 randomly selected grains with different sizes |
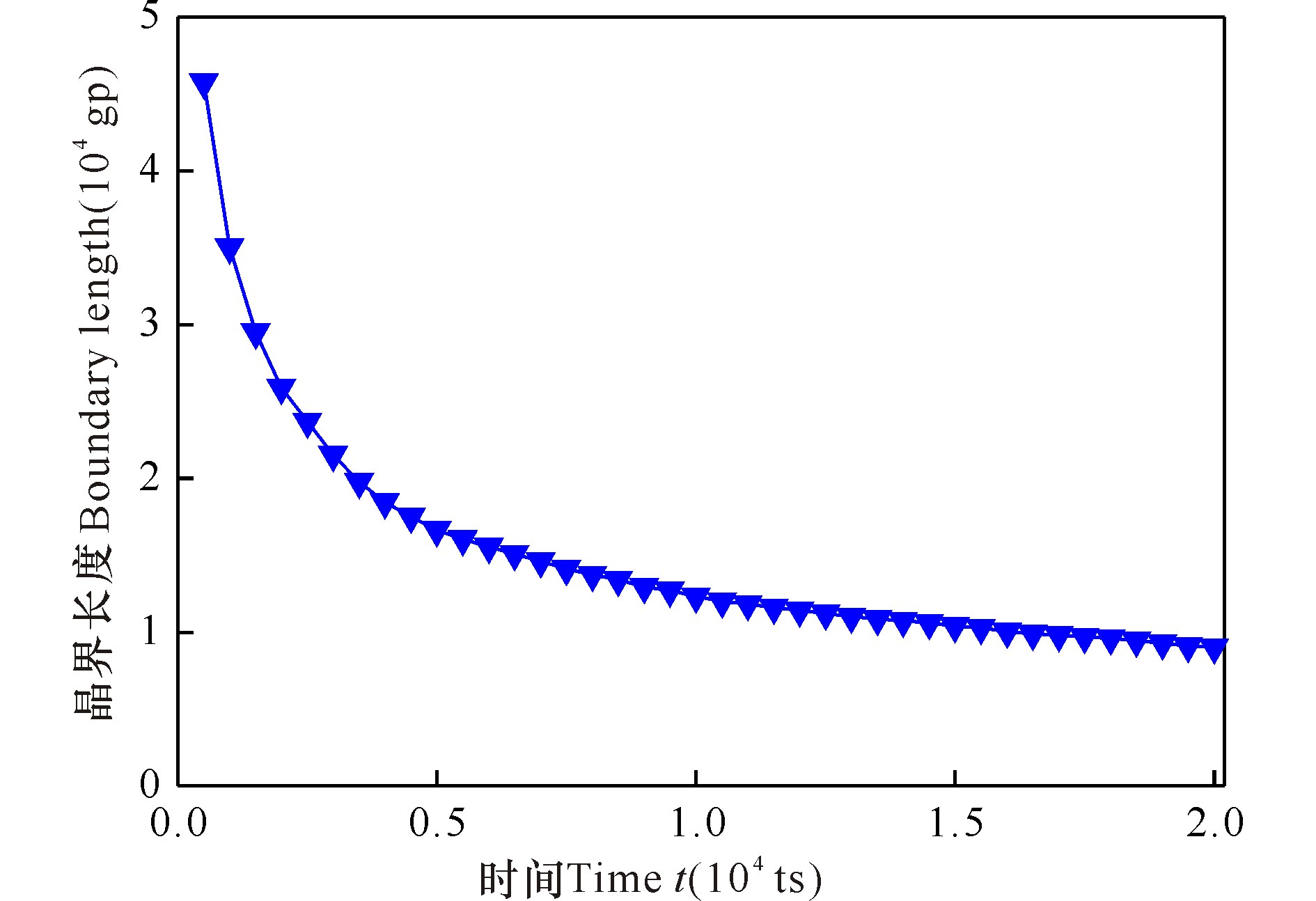
单相多晶系统晶粒演化的驱动力来源于系统界面能的减少,而界面能与晶界长度密切相关[6]。晶粒长大过程中,晶界总长度随演化时间的变化曲线如图 4所示。可见,在演化过程中晶界长度不断减小,减小幅度由快变慢。说明在晶粒长大过程中系统界面能不断降低,遵循能量降低原则。
|
图 4 晶粒长大过程中晶界总长度与演化时间的关系 Fig.4 Total length of grain boundary with time during grain growth |
为研究初始状态为柱状晶粒的生长动力学,设置了长宽比不同且平均晶粒尺寸相同(初始平均晶粒尺寸R0为13 gp)的3种初始柱状微结构,如图 5所示。然后对系统进行均匀退火,即进行正常晶粒演化,所得结果见图 6。

|
(a)Aspect ratio=2.2;(b)Aspect ratio=4.4;(c)Aspect ratio=7.6 图 5 3种不同长宽比的初始柱状微结构 Fig.5 Initial columnar microstructures with three dif-ferent grain aspect ratio |

|
(a1)~(c1)1×103 ts;(a2)~(c2)1×104 ts;(a1),(a2) Initial aspect ratio=2.2;(b1),(b2) Initial aspect ratio=4.4;(c1),(c2) Initial aspect ratio=7.6 图 6 3种不同初始长宽比的柱状微结构的演化过程 Fig.6 Evolution process of columnar microstructures with three different initial aspect ratios |
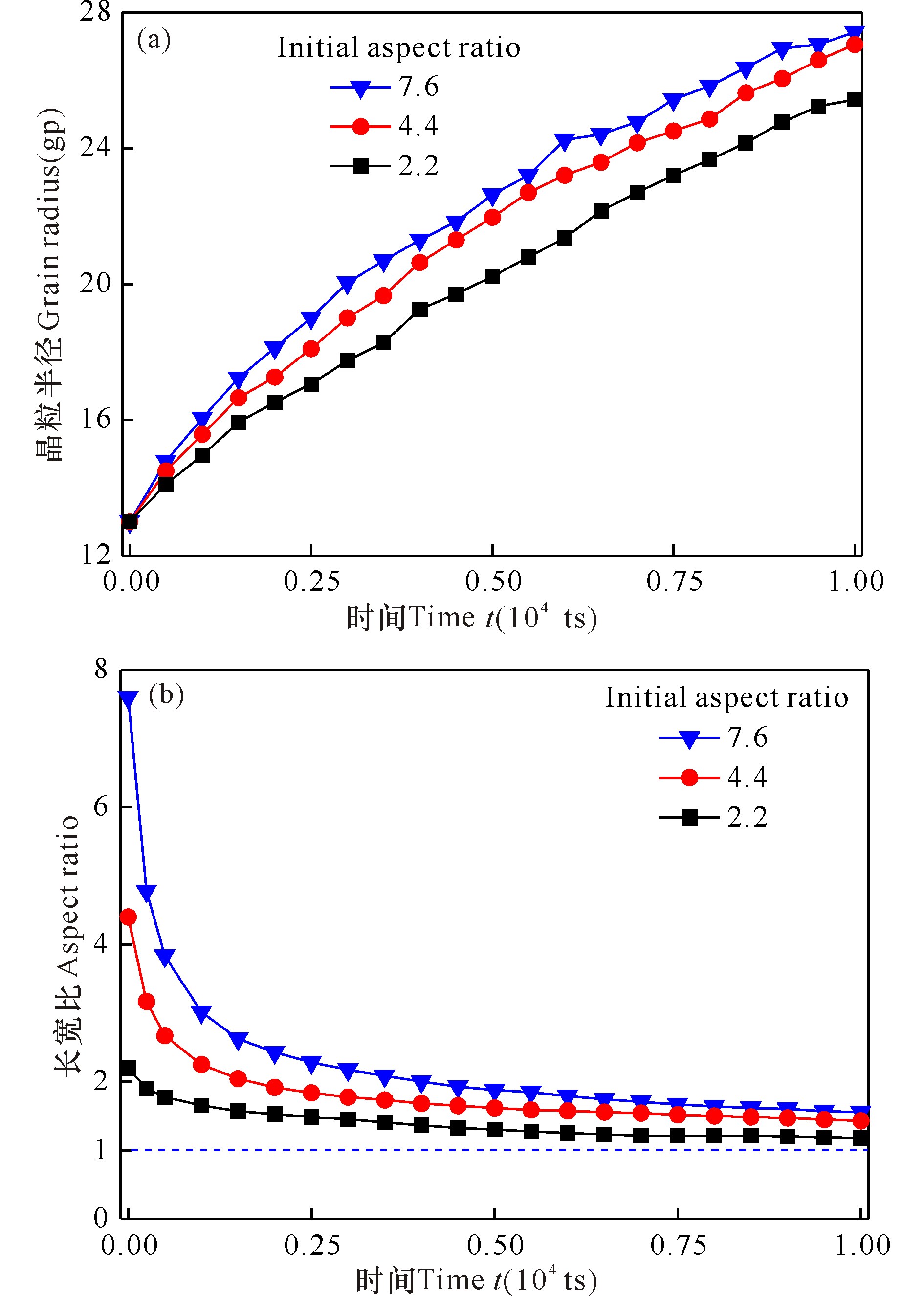
图 6显示了晶粒长大过程中柱状微结构向等轴微结构转变过程。为定量证实该转变现象,统计了3种不同初始长宽比的柱状微结构的平均晶粒尺寸和长宽比与演化时间的关系,如图 7所示。由图 7a可见,晶粒尺寸随初始长宽比的增大而增大。这是因为图 5中晶粒为扁平状或竹节状,其晶界上下方向较平直,而左右方向具有较大曲率,且晶粒长宽比越大,晶粒左右方向的晶界曲率也越大,在演化过程中晶界曲率驱使晶界更快地迁移,晶粒生长就越快。从图 7b可以看出,在晶粒演化过程中,晶粒长宽比不断减小,且减小幅度随初始长宽比的增加而增大。该结果与冷轧钢在退火过程中晶粒长宽比随退火时间变化的规律[16]一致。
|
图 7 柱状微结构的平均晶粒尺寸(a)和长宽比(b)与演化时间的关系 Fig.7 Changes of average grain size (a) and aspect ratio (b) of columnar microstructure with time |
利用局部退火条件下线性温度梯度方法[4],获得梯度指数不同且平均晶粒尺寸相同(平均晶粒半径R0=13 gp)的3种梯度微结构,如图 8所示。其中,梯度指数是系统底部与顶部区域平均晶粒尺寸的比值。由图 8可见,系统顶部的晶粒细小均匀,而系统底部的晶粒较粗大,且梯度指数越大,系统底部晶粒的平直晶界就越多,夹角趋于稳定值120°的三叉晶界也越多。

|
(a)Gradation index=3.2;(b)Gradation index=5.3;(c)Gradation index=8.4 图 8 3种不同梯度指数的初始微结构 Fig.8 Initial microstructures with three different gradation indexes |
为研究梯度微结构的晶粒长大行为,对具有不同梯度指数的微结构进行均匀退火处理,即进行正常晶粒演化,所得结果如图 9所示。可见,晶粒发生了不同程度的长大,其中越靠近系统顶部的晶粒,长大现象就越明显。这是因为系统顶部的晶粒细小,晶界曲率大,晶界多,使得晶粒长大的驱动力大,晶粒长大速度快;而系统底部的晶粒粗大,大部分晶界已趋于直线,晶粒长大的驱动力较小,因此晶粒长大速度缓慢。

|
(a1)~(c1) 2×103 ts;(a2)~(c2) 1×104 ts;(a1),(a2) Initial gradation index=3.2;(b1),(b2) Initial gradation index=5.3;(c1),(c2) Initial gradation index=8.4 图 9 3种初始梯度指数的梯度微结构的演化过程 Fig.9 Evolution process of graded microstructures with three different initial gradation indexes |
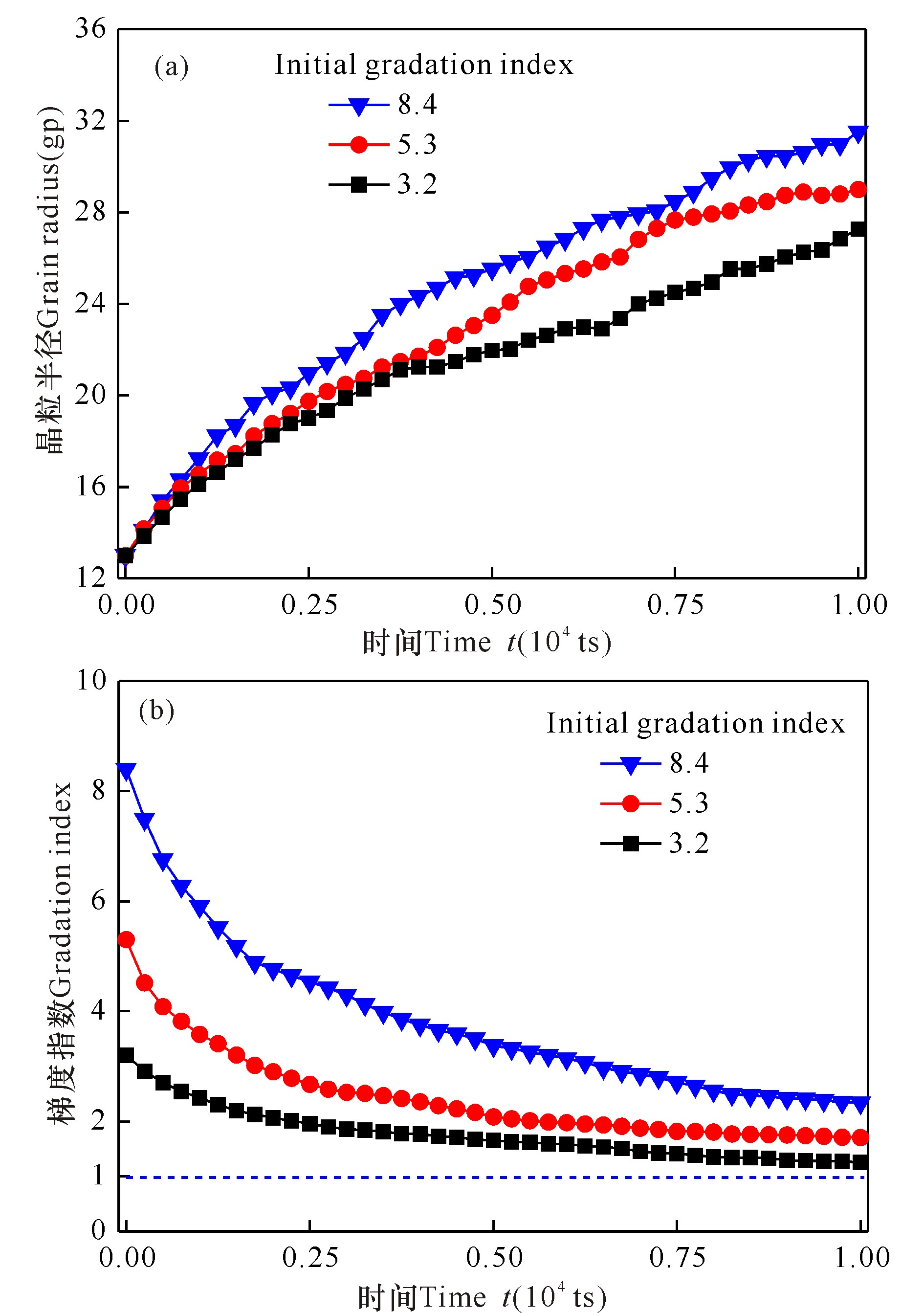
图 10为3种梯度微结构的平均晶粒尺寸和梯度指数随模拟时间的变化曲线。由图 10a可见,平均晶粒尺寸随演化时间的增加而增大,且初始梯度指数越大,晶粒尺寸增长越快。从图 10b可以看出,随着演化时间的增加,3种梯度微结构的梯度指数均逐渐减小,且减小幅度随初始梯度指数的增大而增大。这归因于晶粒长大过程遵循抛物线长大规律,晶粒生长率随晶粒尺寸的增加而减小,导致系统底部的小晶粒比顶部的大尺寸晶粒长得更快,使得梯度指数减小。
|
图 10 梯度微结构的平均晶粒尺寸(a)和梯度指数(b)随演化时间的变化 Fig.10 Changes of average grain size (a) and gradation index (b) of graded microstructure with time |
本研究采用相场法研究二维多晶材料中正常晶粒长大及初态分别为柱状和梯度微结构的晶粒长大过程。研究结果表明,晶粒长大是大晶粒吞噬相邻小晶粒的过程,在此过程中晶界长度不断减小,遵循能量降低原则;正常晶粒长大过程中相对晶粒尺寸分布具有时间不变性特点;柱状微结构的长宽比和梯度微结构的梯度指数均直接影响晶粒长大动力学,这两种初始微结构在演化过程中均向均匀等轴微结构转变;晶界曲率显著影响晶粒长大过程,曲率越大,晶粒长大就越快。
| [1] |
MEYERS M A, CHAWLA K K. Mechanical Behavior of Materials[M]. Cambridge: Cambridge University Press, 2009.
|
| [2] |
GEERS M G D, YVONNET J. Multiscale modeling of microstructure-property relations[J]. MRS Bulletin, 2016, 41(8): 610-616. DOI:10.1557/mrs.2016.165 |
| [3] |
HOLM E A, FOILES S M. How grain growth stops:A mechanism for grain-growth stagnation in pure materials[J]. Science, 2010, 328(5982): 1138-1141. DOI:10.1126/science.1187833 |
| [4] |
GODFREY A W, MARTIN J W. Some Monte Carlo studies of grain growth in a temperature gradient[J]. Philosophical Magazine A, 1995, 72(3): 737-749. DOI:10.1080/01418619508243797 |
| [5] |
WILLIAMSON A, DELPLANQUE J P. Strain energy limitations in Monte Carlo Potts modeling of grain growth[J]. Computational Materials Science, 2015, 108: 48-55. DOI:10.1016/j.commatsci.2015.05.032 |
| [6] |
HE Y Z, DING H L, LIU L F, et al. Computer simulation of 2D grain growth using a cellular automata model based on the lowest energy principle[J]. Materials Science and Engineering:A, 2006, 429(1/2): 236-246. |
| [7] |
RAGHAVAN S, SAHAY S S. Modeling the topological features during grain growth by cellular automaton[J]. Computational Materials Science, 2009, 46(1): 92-99. DOI:10.1016/j.commatsci.2009.01.028 |
| [8] |
CHEN L Q, YANG W. Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters:The grain-growth kinetics[J]. Physical Review B, 1994, 50(21): 15752-15756. DOI:10.1103/PhysRevB.50.15752 |
| [9] |
CHEN L Q, FAN D N. Computer simulation model for coupled grain growth and Ostwald Ripening-application to Al2O3-ZrO2 two-phase systems[J]. Journal of the American Ceramic Society, 1996, 79(5): 1163-1168. DOI:10.1111/jace.1996.79.issue-5 |
| [10] |
KAZARYAN A, WANG Y, DREGIA S A, et al. Grain growth in systems with anisotropic boundary mobility:Analytical model and computer simulation[J]. Physical Review B, 2001, 63(18): 184102. DOI:10.1103/PhysRevB.63.184102 |
| [11] |
KRILL Ⅲ C E, CHEN L Q. Computer simulation of 3-D grain growth using a phase-field model[J]. Acta Materialia, 2002, 50(12): 3059-3075. DOI:10.1016/S1359-6454(02)00084-8 |
| [12] |
魏承炀, 李赛毅. 温度梯度对晶粒生长行为影响的相场模拟[J]. 物理学报, 2011, 60(10): 132-139. WEI C Y, LI S Y. Effect of temperature gradient on grain growth behavior from phase field simulations[J]. Acta Physica Sinica, 2011, 60(10): 132-139. |
| [13] |
KURTZ S K, CARPAY F M A. Microstructure and normal grain growth in metals and ceramics.Part Ⅱ.Experiment[J]. Journal of Applied Physics, 1980, 51(11): 5745-5754. DOI:10.1063/1.327581 |
| [14] |
LOUAT N P. On the theory of normal grain growth[J]. Acta Metallurgica, 1974, 22(6): 721-724. DOI:10.1016/0001-6160(74)90081-9 |
| [15] |
SAHAY S S, MALHOTRA C P, KOLKHEDE A M. Accelerated grain growth behavior during cyclic annealing[J]. Acta Materialia, 2003, 51(2): 339-346. DOI:10.1016/S1359-6454(02)00398-1 |
| [16] |
SAHAY S S, KUMAR B V H, KRISHNAN S J. Microstructure evolution during batch annealing[J]. Journal of Materials Engineering and Performance, 2003, 12(6): 701-707. DOI:10.1361/105994903322692510 |
 2016, Vol. 23
2016, Vol. 23 


