【研究意义】机组组合(unit commitment,UC)是电力系统运行调度一个非常重要的方面,同时也是一个非常活跃的研究领域。经典的UC问题是指在一个调度周期内满足系统预测负荷需求和旋转备用等约束条件下,确定机组的启停计划和机组出力情况,从而使发电总费用最小[1]。UC问题在数学上常被描述成一个大规模的混合整数组合优化问题,含有大量表示机组启停状态的0-1变量和表示机组出力的连续变量。【前人研究进展】迄今为止,几乎所有用于求解混合整数规划问题的确定性方法[2-7]以及源于对一些生物和社会现象的模拟而产生的智能算法[8-9]都被尝试用于求解UC问题,但由于其可行解集的组合性质,该问题很难在多项式时间内有效求解。此外,近年来由于大量温室气体排放所导致的全球变暖已成为全世界共同关心的重点问题,而电力工业是温室气体的排放大户,占全球二氧化碳(CO2)总排放的40%,因此,考虑计及CO2排放的UC问题并进行有效求解具有非常重要的应用价值[10-12]。【本研究切入点】分解法是求解大规模复杂问题的一种常用技术,其基本思想是先将复杂问题分解为相对容易求解的主问题和子问题,然后通过逐次交替迭代求解这两个问题来达到求解原复杂问题的目的。这类方法主要包括Benders分解法[13-14]和外逼近法[15],并且已被尝试用于求解经典的UC问题[16-19]。然而当前Benders分解法在求解各类复杂问题时存在一个计算方面的瓶颈——由于其在每次迭代中仅加入一个相应的Benders割平面,所以该方法计算效率较低。【拟解决的关键问题】本文提出能有效求解计及CO2排放UC问题的一个加速广义Benders分解法,并将其在10~100台机组24时段等6个系统上进行数值测试,同时将测试结果与其他方法的结果进行比较。
1 计及CO2排放UC问题的混合整数二次规划模型计及CO2排放UC问题的目标函数是让发电机组的运行成本Fc与排放成本Ec加权和求最小,即
| $\begin{matrix} min & ~{{T}_{c}}={{w}_{f}}{{F}_{c}}+{{w}_{e}}{{E}_{c}}, \\ \end{matrix}$ | (1) |
式中wf,we为各成本所占权重系数,Fc与Ec的具体表达式如下:
| ${{F}_{c}}=\sum\limits_{t=1}^{T}{\sum\limits_{i=1}^{N}{[{{\alpha }_{i}}{{u}_{i,t}}+{{\beta }_{i}}{{P}_{i,t}}+{{\gamma }_{i}}{{({{P}_{i,t}})}^{2}}+{{u}_{i,t}}(1-{{u}_{i,t-1}}){{C}_{i,t}}],}}$ | (2) |
| ${{E}_{c}}=\sum\limits_{t=1}^{T}{\sum\limits_{i=1}^{N}{[{{\pi }_{i}}({{a}_{i}}+{{b}_{i}}{{P}_{i,t}}+{{c}_{i}}{{({{P}_{i,t}})}^{2}})]{{u}_{i,t}},}}$ | (3) |
其中N为机组总数,i=1,2,…,N为机组标号;T为时段总数,t=1,2,…,T为时段标号;αi,βi,γi为机组i的发电费用参数;Ci,t为机组启动费用;πi为机组i的排放惩罚因子;ai,bi,ci为机组i的耗量特性参数。此外,ui,t为0-1整数变量,表示机组i在第t时段的状态,值为1时表示机组i处于运行状态,值为0时表示机组i处于停机状态;Pi,t为连续变量,表示机组i在第t时段的出力。
计及CO2排放UC问题的约束条件如下:
| $①功率平衡约束\sum\limits_{i=1}^{N}{{{P}_{i,t}}-{{P}_{D,t}}=0},$ | (4) |
| $②机组出力约束{{u}_{i,t}}\underline{{{P}_{i}}}\le {{P}_{i,t}}\le {{u}_{i,t}}{{\overline{P}}_{i}},$ | (5) |
③爬坡约束
| $\left\{ \begin{matrix} {{P}_{i,t}}-{{P}_{i,t-1}}\le {{u}_{i,t-1}}{{P}_{up,i}}+({{u}_{i,t}}-{{u}_{i,t-1}}){{P}_{start,i}}+\left( 1-{{u}_{i,t}} \right){{\overline{P}}_{i}}, \\ {{P}_{i,t-1}}-{{P}_{i,t}}\le {{u}_{i,t}}{{P}_{down,i}}+({{u}_{i,t1}}-{{u}_{i,t}}){{P}_{shut,i}}+\left( 1-{{u}_{i,t-1}} \right){{\overline{P}}_{i}}, \\ \end{matrix} \right.$ | (6) |
| $④旋转备用约束\sum\limits_{i=1}^{N}{{{\overline{P}}_{i}}}\ge {{P}_{D,t}}+{{R}_{t}},$ | (7) |
⑤最小启停时间约束
| $\left\{ \begin{matrix} \left( {{u}_{i,t-1}}-{{u}_{i,t}} \right)\left( {{T}_{i,t-1}}-{{\underline{T}}_{on,i}} \right)\ge 0, \\ ({{u}_{i,t}}-{{u}_{i,t-1}})(-{{T}_{i,t-1}}-{{\underline{T}}_{off,i}})\ge 0. \\ \end{matrix} \right.$ | (8) |
上述约束条件中参数PD,t为系统第t时段的总负荷;Pi,${{\overline{P}}_{i}}$分别为机组i的最小和最大出力;Pup,i,Pstart,i,Pdown,i,Pshut,i分别为机组i的功率上升速度限制、启动功率速度限制、功率下降速度限制及停机功率速度限制;Rt为系统第t时段的总备用;Ton,i、Toff,i分别为机组i的最小运行时间与最小停机时间;Ti,t为机组i在第t时段已连续运行时间(为正值)或连续停机时间(为负值)。对于式(2)中的非线性启动费用项,借助于文献[3]中的技术对其进行线性化处理,即首先令Si,t=ui,t(1-ui,t-1)Ci,t,然后应用如下线性阶梯函数把Si,t进行近似转化:
| $\left\{ \begin{matrix} {{S}_{i,t}}\ge {{K}_{i,\tau }}\left[ {{u}_{i,t}}-\sum _{j=1}^{\tau }{{u}_{i,t-j}} \right], \\ {{S}_{i,t}}\ge 0,i=1,\ldots ,N;t=1,\ldots ,T;\tau =1,\ldots ,{{N}_{Di}}, \\ \end{matrix} \right.$ |
式中NDi是给定参数,系数Ki,τ则由下述分段函数表示:
| $\left\{ \begin{matrix} {{K}_{i,\tau }}=\text{ }{{C}_{hot,i}}:\tau =1,\ldots ,{{T}_{off,i}}+{{T}_{cold,i}}, \\ {{C}_{cold,i}}:\tau ={{T}_{off,i}}+{{T}_{cold,i}}+1,\ldots ,{{N}_{Di}}, \\ \end{matrix} \right.$ |
其中Chot,i、Ccold,i分别为机组i的热启动费用与冷启动费用;Tcold,i为机组i的冷启动时间。此外,对于时间耦合且离散的非线性最小启停时间约束(8),则利用文献[20]中方法进行线性化处理,具体表示如下:
| $\left\{ \begin{matrix} \sum\limits_{\overline{\omega }max\left( t-{{\underline{T}}_{on,i}}+1,1 \right)}^{t}{{{W}_{i,\overline{\omega }}}\le {{u}_{i,t}}},t\in \left[ {{U}_{i}}+1,\ldots ,T \right], \\ \sum\limits_{\overline{\omega }max\left( t-{{\underline{T}}_{off,i}}+1,1 \right)}^{t}{{{W}_{i,\overline{\omega }}}\le 1-{{u}_{i,t-\tau }},} \\ t\in \left[ {{L}_{i}}+1,\ldots ,T \right], \\ 1\ge {{W}_{i,t}}\ge {{u}_{i,t}}-{{u}_{i,t-1}},{{W}_{i,t}}\ge 0, \\ t\in \left[ 2,\ldots ,T \right], \\ {{u}_{i,t}}={{u}_{i,0}},t\in [1,\ldots ,{{U}_{i}}+{{L}_{i}}] \\ \end{matrix} \right.$ |
式中Wi,t是新引进的变量,其表示机组i在第t时段的启动状态,其余参数定义如下:
| $\left\{ \begin{matrix} \begin{align} & {{U}_{i}}=max~\left\{ 0,min\left[ T,{{u}_{i,0}}\left( {{\underline{T}}_{on,i}}-{{T}_{i,0}} \right) \right] \right\}, \\ & \tau =min\left\{ {{\underline{T}}_{off,i}},t \right\}, \\ \end{align} \\ {{L}_{i}}=max~\{0,min[T,(1-{{u}_{i,0}})({{\underline{T}}_{off,i}}+{{T}_{i,0}})]\} \\ \end{matrix} \right.$ |
基于以上分析,计及CO2排放UC问题可方便地描述为如下近似混合整数二次规划(mixed integer quadratic programming,MIQP)模型:
| $\begin{align} & \begin{matrix} min & {{w}_{f}}\sum\limits_{t=1}^{T}{\sum\limits_{i=1}^{N}{\left( {{\alpha }_{i}}{{u}_{i,t}}+{{\beta }_{i}}{{P}_{i,t}}+{{\gamma }_{i}}{{\left( {{P}_{i,t}} \right)}^{2}}+{{S}_{i,t}} \right)}} \\ \end{matrix} \\ & +{{w}_{e}}\left( \sum\limits_{t=1}^{T}{\sum\limits_{i=1}^{N}{\left[ {{\pi }_{i}}{{u}_{i,t}}\left( {{a}_{i}}+{{b}_{i}}{{P}_{i,t}}+{{c}_{i}}{{\left( {{P}_{i,t}} \right)}^{2}} \right) \right]}} \right) \\ & \begin{matrix} ~s.t.~ & {{A}_{u}}u+{{A}_{P}}P+{{A}_{S}}S+{{A}_{W}}W\le {{a}_{uc}}, \\ \end{matrix} \\ & u=\left( {{u}_{i,t}} \right),P=\left( {{P}_{i,t}} \right),S=\left( {{S}_{i,t}} \right),W=\left( {{W}_{i,t}} \right), \\ & {{u}_{i,t}}\in \left\{ 0,1 \right\},{{P}_{i,t}},{{S}_{i,t}}\ge 0,{{W}_{i,t}}\in [0,~1], \\ & i=1,\ldots ,N,t=1,\ldots ,T, \\ \end{align}$ | (9) |
式中u,P,S,W为相应变量所组成的向量,Au,AP,AS,AW是相应变量所对应的系数矩阵,auc则为右端常数向量。
2 计及CO2排放UC问题的加速广义Benders分解法 2.1 广义Benders分解法广义Benders分解法(generalized Benders decomposition method,GBDM)[14]可直接用于求解混合整数非线性规划(mixed integer nonlinear programming,MINLP)问题,下面结合UC问题特点,以如下形式的MINLP问题为例简单介绍GBDM:
| $\begin{matrix} min & {{c}^{T}}y+f\left( x \right) \\ s.t. & \begin{align} & h\left( x \right)=0, \\ & By+Cx\le b, \\ & Dy\le d, \\ & x\in {{R}^{n}},y\in {{\left\{ 0,1 \right\}}^{m}}, \\ \end{align} \\ \end{matrix}$ | (10) |
其中f(x)是光滑的非线性函数,h(x)是非线性向量值函数,B,C,D是相应系数矩阵,c,b,d是常数向量。对于当前给定的整数变量值yk,GBDM形成如下非线性子问题:
| $\begin{matrix} min & {{c}^{T}}{{y}^{k}}+f\left( x \right) \\ s.t. & h\left( x \right)=0, \\ {} & B{{y}^{k}}+Cx\le b \\ \end{matrix}$ | (11) |
如果子问题(11)有解,并记其解为xk,且λk为对应于不等式约束Byk+Cx≤b的乘子向量,则根据这些数据可得到下述最优性Benders割平面:
| ${{c}^{T}}y+f({{x}^{k}})+{{({{\lambda }^{k}})}^{T}}(C{{x}^{k}}+By-b)\le \mu $ | (12) |
相反,若子问题(11)无解,则求解下述可行性子问题
| $\begin{matrix} min & \eta \\ s.t. & h\left( x \right)=0, \\ {} & B{{y}^{k}}+Cx-\eta \le b \\ \end{matrix}$ | (13) |
注意到子问题(13)一定有解,并记其解为(xFk,ηFk)且λFk为对应于不等式约束Byk+Cx-η≤b的乘子向量,于是形成下述可行性Benders割平面:
| ${{({{\lambda }^{k}}_{F})}^{T}}(By+C{{x}^{k}}_{F}-b)\le 0$ | (14) |
此外,GBDM中的主问题形式如下:
| $\begin{align} & \begin{matrix} min & \mu \\ \end{matrix} \\ & Dy\le d \\ & {{c}^{T}}y+f\left( {{x}^{k}} \right)+{{\left( {{\lambda }^{k}} \right)}^{T}}\left( By+C{{x}^{k}}-b \right)\le \mu , \\ & {{\left( {{\lambda }^{k}}_{F} \right)}^{T}}\left( By+C{{x}^{k}}_{F}-b \right)\le 0, \\ & \mu \in R,y\in {{\left\{ 0,1 \right\}}^{m}} \\ \end{align}$ | (15) |
下面给出GBDM求解问题(10)的基本步骤。
初始步 取初始上界UB=∞,同时选取初始整数变量值yk,并令k:=0。
步骤1 形成并求解子问题。
若子问题(11)有最优解,则可得到相应最优性Benders割平面,若进一步还有
| $UB>{{c}^{T}}{{y}^{k}}+f({{x}^{k}}),$ |
则令UB=cTyk+f(xk),x*=xk,y*=yk;
若子问题(11)无解,则求解可行性子问题(13),并得到可行性Benders割平面或者直接计算如下组合Benders割平面[21],
| ${{\sum }_{j\in {{S}_{one}}}}{{y}_{j}}-{{\sum }_{j\in {{S}_{zero}}}}{{y}_{j}}\le |{{S}_{one}}|-1,$ | (16) |
其中Sone={j:yjk=1},Szero={j:yjk=0},|·|表示集合中元素个数。
步骤2 求解主问题。
将步骤1中所产生的割平面加入到上一次的主问题(15)中,重新求解主问题,并记yk+1为主问题最优解中对应于整数变量的值,zmilp为相应的最优值。若zmilp≥UB,则算法终止,当前(x*,y*)就是原MINLP问题(10)的最优解;否则,令k:=k+1,返回步骤1。
2.2 UC问题的整数割平面UC问题整数割平面的导出是源于对其一种非常自然的理解,即先去找每个时段必须投入运行机组数的有效下界,因此对于每个时段先求解如下线性规划问题:
| $\begin{align} & \begin{matrix} min~ & {{U}_{t}} \\ s.t.~ & {{U}_{t}}=\sum _{i=1}^{N}{{u}_{i,t}}, \\ \end{matrix} \\ & {{A}_{u}}u+{{A}_{P}}P+{{A}_{S}}S+{{A}_{W}}W\le {{a}_{uc}}, \\ & u=\left( {{u}_{i,t}} \right),P=\left( {{P}_{i,t}} \right),S=\left( {{S}_{i,t}} \right),W=\left( {{W}_{i,t}} \right), \\ & {{u}_{i,t}}\in [0,~1],{{P}_{i,t}},{{S}_{i,t}}\ge 0,{{W}_{i,t}}\in [0,~1], \\ & i=1,\ldots ,N,t=1,\ldots ,T \\ \end{align}$ | (17) |
注意到上述线性规划问题(17)一定有解,事实上除将原整数变量进行连续松弛外,问题(17)的其余约束与近似MIQP模型(9)完全一样。记U2opt为线性规划问题(17)的最优值,并且令U2low=U2opt,则下述整数不等式(18)由于能够割除MIQP模型(9)的连续松弛问题在部分非整数ui,t处的可行解,同时又不影响原MIQP的求解,故其为MIQP模型(9)的有效割平面,并称其为整数割平面:
| $\sum\limits_{i=1}^{N}{{{u}_{i,t}}}\ge {{U}^{low}}_{t}\left( t=1,\ldots ,T \right)$ | (18) |
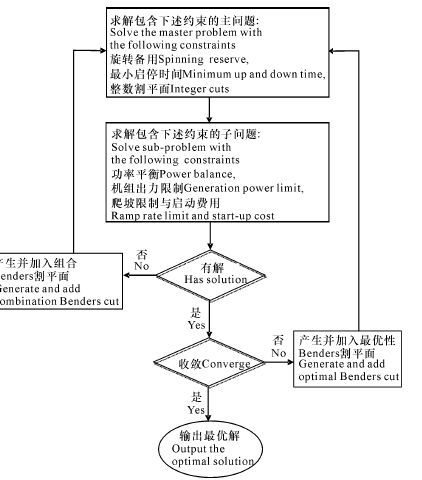
首先根据前面所述内容可知计及CO2排放UC问题的近似MIQP模型中仅在目标函数中出现非线性项,若将该项除去,所求问题便变成一个混合整数线性规划(mixed integer linear programming,MILP),其与原MIQP有相同的可行域,因此在不追求精度的情况下,可调用著名商业软件CPLEX快速得到MILP的一个可行解,从而计算出原MIQP目标函数值的一个上界。其次,在应用GBDM求解MIQP时,初始主问题是原MIQP的一个松弛问题,仅包含原问题的部分约束和变量,故其最优值是原MIQP目标函数值的一个下界。而2.2节所提的整数割平面仅含有0-1整数变量,并且加入这些割平面可以使得原MIQP的连续松弛问题变紧,故在应用GBDM求解相关UC问题时,相应的主问题也会变紧,从而能够提供一个更好的下界。此外,为进一步减少计算量,当相应的非线性子问题(11)不可行时,不去计算相应的可行性子问题,而是直接利用显式公式(16)计算相应的组合Benders割平面。基于前述技术,可得到求解计及CO2排放UC问题的一个加速广义Benders分解法,具体算法流程如图 1所示。
|
图 1 算法流程图 Fig.1 Flow chat of algorithm |
为方便起见,将本文所提出的加速广义Benders分解法简记为AGBDM,为验证其计算效率,下面就不计CO2排放UC问题情形在10~100台机组24时段等6个系统上进行测试,并将测试结果与已有的Berders分解法以及另外一些有效方法进行比较,同时以10台机组24时段系统为例详细说明该方法求解计及CO2排放UC问题的有效性。10台机组24时段系统的基本数据取自文献[2],20~100台机组的相关数据是通过复制10台机组24时段系统的基本数据得到,而CO2排放数据则来源于文献[22]。旋转备用取总负荷的10%。运行环境为AMD Athlon Dual Core Processor 4400+ 2.3 GHz,1 GB RAM,并在Matlab 2010环境下调用CPLEX 11[23]求解主问题与子问题以及相应线性规划问题。此外,在调用CPLEX得到相应可行解时精度取为0.05。
3.1 不计CO2排放UC问题情形为验证本文所提AGBDM在求解不计CO 2排放UC(此时wf=1,we=0)问题时的加速效果,对于不计爬坡约束情形,将相同精度下的测试结果同时与广义Benders分解法[18] (简记为GBDM) 以及松弛型Benders分解法[19] (简记为RBDM) 所得结果进行比较(表 1),其中Niter表示迭代次数,CPU表示计算时间,Cost表示总费用,数据中的粗体部分表示最好结果,后面表格中的记法类似。通过表 1可以看出本文所提AGBDM均能在合理的时间内经过一次迭代后便收敛,说明该方法具有良好的稳定性。此外,除10台机组与20台机组24时段两个较小的系统外,其他系统的测试结果均优于另外两种方法,这也说明整数割平面以及2.3节所介绍的加速技术能很好地改进Benders分解法求解UC问题的计算效果,也正是因为AGBDM在求解相关问题时可得到更好的上下界,所以整个算法的迭代次数要少。
| 表 1 10~100台机组24时段系统3种算法结果比较 Table 1 The results of three algorithms for 10~100 units and 24 hours |
为进一步说明本文所提AGBDM求解相关UC问题的有效性,对于不计爬坡约束情形,将其测试结果同当前一些数值表现良好的确定性方法如拉格朗日松弛(LR)法[2]、混合整数线性规划(MILP)法[3]、二阶锥规划(CONE)法[5]、外逼近法(OAM)[16]、内外逼近法(OIAM)[17]等进行比较(表 2),表中记号“—”表示原文中没有给出相应结果。通过表 2可以看出:对于40台机组与80台机组这两个系统,AGBDM的测试结果优于当前最好的内外逼近法,而其余系统的计算结果稍稍逊于最好结果。此外,作为测试效果优秀的外逼近与内外逼近,在求解相关UC问题时其迭代次数均为两次,而本文所提AGBDM由于加入整数割平面,并利用2.3节所介绍的加速技术,其迭代次数均为1次。
| 表 2 10~100台机组24时段系统不同算法结果比较($) Table 2 The results of different algorithms for 10~100 units and 24 hours ($) |
将本文所提的AGBDM应用于计及爬坡约束UC问题情形。取机组的爬坡速率限制分别为Pup,i=Pdown,i=20%$\overline{P}$i,Pstart,i=Pshut,i=2$\overline{P}$i,如表 3所示,本文所提AGBDM均能在合理的时间内获得相关UC问题较高质量的解,表明本文所提方法能有效求解计及爬坡约束UC问题,并且可用于有效求解其他类型的UC问题。
| 表 3 10~100台机组24时段系统(计及爬坡约束) Table 3 System for 10~100 units and 24 hours(with ramp rate constraints) |
类似于文献[22],下面仅以10台机组24时段系统并计及爬坡约束为例,详细说明本文所提AGBDM求解计及CO2排放UC问题的有效性。在数值测试中取权重因子wf=we=1。根据表 4可以看出所考察系统在24时段内所排放的CO2总额为260 067(Ton),若取排放惩罚因子πi=1$Ton(i=1,…,N),则排放费用为260 067$。由此可见,排放费用不容忽视,特别是在大力倡导节能减排以及高科技发展迅速的今天,很有必要在经典电力系统机组组合问题中考虑一些清洁可再生能源,如结合太阳能发电、风力发电以及可入网电动汽车等。
4 结论本文提出计及CO2排放UC问题的一个加速广义Benders分解法,首先利用线性化技术建立一个近似MIQP模型,然后结合UC问题特点提出一个针对机组组合问题而言非常简单却效果很明显的有效割平面——整数割平面,同时基于该整数割平面以及文中所介绍的加速技术提出求解相关UC问题近似MIQP模型的加速广义Benders分解法,最后将所提方法在不同系统上进行数值测试。不同情形下的测试结果以及与当前其他一些有效方法的比较表明,本文所提方法能有效求解相关UC问题,并且具有良好的稳定性和收敛性。
| 表 4 10台机组24时段系统调度计划及CO2排放情况 Table 4 Unit scheduling and corresponding costs for the 10 units and 24 hours system |
| [1] |
SHEBL G B, FAHD G N. Unit commitment literature synopsis[J]. IEEE Transactions on Power Systems, 1994, 9(1): 128-135. DOI:10.1109/59.317549 |
| [2] |
ONGSAKUL W, PETCHARAKS N. Unit commitment by enhanced adaptive lagrangian relaxation[J]. IEEE Transactions on Power Systems, 2004, 19(1): 620-628. DOI:10.1109/TPWRS.2003.820707 |
| [3] |
CARRION M, ARROYO J M. A computationally effi-cient mixed-integer linear formulation for the thermal unit commitment problem[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1371-1378. DOI:10.1109/TPWRS.2006.876672 |
| [4] |
全然, 简金宝, 韦化, 等. 基于特殊有效不等式求解机组组合问题的内点割平面法[J]. 中国电机工程学报, 2011, 31(19): 51-59. QUAN R, JIAN J B, WEI H, et al. An interior-point cutting plane method for unit commitment based on special valid inequalities[J]. Proceedings of the CSEE, 2011, 31(19): 51-59. |
| [5] |
YUAN X H, TIAN H, ZHANG S Q. Second-order cone programming for solving unit commitment strategy of thermal generators[J]. Energy Conversion and Management, 2013, 76: 20-25. DOI:10.1016/j.enconman.2013.07.019 |
| [6] |
YANG L F, JIAN J B, ZHU Y N, et al. Tight relaxation method for unit commitment problem using reformulation and lift-and-project[J]. IEEE Transactions on Power Systems, 2015, 30(1): 13-23. DOI:10.1109/TPWRS.2014.2326920 |
| [7] |
ZHENG H Y, JIAN J B, YANG L F, et al. A deterministic method for the unit commitment problem in power systems[J]. Computers & Operations Research, 2016, 66: 241-247. |
| [8] |
KAZARLIS S A, BAKIRTZIS A G, PETRIDIS V. A genetic algorithm solution to the unit commitment problem[J]. IEEE Transactions on Power Systems, 1996, 11(1): 83-92. DOI:10.1109/59.485989 |
| [9] |
MANTAWY A H, ABDEL-MAGID Y L, SELIM S Z. Unit commitment by tabu search[J]. IEE Proceedings-Generation,Transmission and Distribution, 1998, 145(1): 56-64. DOI:10.1049/ip-gtd:19981681 |
| [10] |
GJENGEDAL T. Emission constrained unit-commitm-ent(FCUC)[J]. IEEE Transactions on Energy Conversion, 1996, 11(1): 132-138. DOI:10.1109/60.486587 |
| [11] |
张晓花, 赵晋泉, 陈星莺. 节能减排多目标机组组合问题的模糊建模及优化[J]. 中国电机工程学报, 2010, 30(22): 71-76. ZHANG X H, ZHAO J Q, CHEN X Y. Multi-objective unit commitment fuzzy modeling and optimization for energy-saving and emission reduction[J]. Proceedings of the CSEE, 2010, 30(22): 71-76. |
| [12] |
XIE J, ZHONG J, LI Z, et al. Environmental-economic unit commitment using mixed-integer linear programming[J]. European Transactions on Electrical Power, 2011, 21(1): 772-786. DOI:10.1002/etep.476 |
| [13] |
BENDERS J F. Partitioning procedures for solving mixed-variables programming problems[J]. Numerische Mathematik, 1962, 4(1): 238-252. DOI:10.1007/BF01386316 |
| [14] |
GEOFFRION A M. Generalized benders decomposition[J]. Journal of Optimization Theory and Applications, 1972, 10(4): 237-260. DOI:10.1007/BF00934810 |
| [15] |
DURAN M A, GROSSMANN I E. An outer-approximation algorithm for a class of mixed-integer nonlinear programs[J]. Mathematical Programming, 1986, 36(3): 307-339. DOI:10.1007/BF02592064 |
| [16] |
全然, 简金宝, 郑海艳. 基于外逼近方法的中期机组组合问题[J]. 电力系统自动化, 2009, 33(11): 24-28. QUAN R, JIAN J B, ZHENG H Y. Medium term unit commitment based on outer approximation method[J]. Automation of Electric Power Systems, 2009, 33(11): 24-28. |
| [17] |
HAN D L, JIAN J B, YANG L F. Outer approximation and outer-inner approximation approaches for unit commitment problem[J]. IEEE Transactions on Power Systems, 2014, 29(2): 505-513. DOI:10.1109/TPWRS.2013.2253136 |
| [18] |
RAHIMI S, NIKNAM T, FALLAHI F. A new approa-ch based on Benders decomposition for unit commitment problem[J]. World Applied Sciences Journal, 2009, 6(12): 1665-1672. |
| [19] |
郑海艳, 简金宝, 全然, 等. 基于改进的Benders分解与透视割平面的机组组合算法[J]. 电力自动化设备, 2015, 35(1): 133-138. ZHENG H Y, JIAN J B, QUAN R, et al. Unit commitment algorithm based on improved Benders decomposition and perspective cut[J]. Electric Power Automation Equipment, 2015, 35(1): 133-138. |
| [20] |
OSTROWSKI J, ANJOS M F, VANNELLI A. Tight mixed integer linear programming formulations for the unit commitment problem[J]. IEEE Transactions on Power Systems, 2012, 27(1): 39-46. DOI:10.1109/TPWRS.2011.2162008 |
| [21] |
CODATO G, FISCHETTI M. Combinatorial Benders' cuts for mixed-integer linear programming[J]. Operations Research, 2006, 54(4): 756-766. DOI:10.1287/opre.1060.0286 |
| [22] |
陆凌蓉, 文福栓, 薛禹胜, 等. 计及可入网电动汽车的电力系统机组最优组合[J]. 电力系统自动化, 2011, 35(21): 16-20. LU L R, WEN F S, XUE Y S, et al. Unit commitment in power systems with plug-in electric vehicles[J]. Automation of Electric Power Systems, 2011, 35(21): 16-20. |
| [23] |
KENNETH H,ANDERS O G,MARCUS M E.User's guide for TOMLAB /CPLEX v11.2[EB/OL].[2008-02-08].http://tomopt.com/tomlab/download/manuals.php.
|
 2016, Vol. 23
2016, Vol. 23 

