混沌系统的控制与同步是当代非线性科学的研究热点.随着控制工程与控制理论的发展,人们提出了不同的控制策略.如文献[1]和文献[2]分别应用线性反馈和非线性反馈控制方法研究混沌系统的同步问题;文献[3]利用自适应控制策略研究一类非线性系统的非光滑观测器的设计问题;文献[4]和文献[5]分别运用反步设计和滑膜控制研究混沌系统的同步问题;文献[6-10]基于线性矩阵不等式,通过脉冲控制策略建立混沌系统的同步判据;文献[11-14]通过间歇控制探讨系统的同步问题.在以上的控制策略中,不连续的控制有脉冲控制和间歇控制.与连续控制相比,不连续控制的控制成本低,容易实施并且具有较强的鲁棒性.不连续控制中,脉冲控制只是在某些离散点处进行控制.间歇控制是控制器工作一段时间之后再休息一段时间,如此周而复始.间歇控制使系统具有更好的闭环性能和较高的控制成本.故间歇控制策略被广泛应用于系统镇定[15-17]与同步[18]研究以及观测器设计[19]等方面.然而,上述文献的间歇控制的控制窗口宽度与休息宽度都是固定的,也即周期间歇控制.但实际应用中要求控制是周期的,这是不合理的或者是不必要的.某些情况下,非周期间歇更符合实际系统的应用.例如,风能发电或太阳能发电系统是经典的非周期间歇控制系统.文献[20-21]应用非周期间歇控制研究系统的镇定与同步.
而在实际操作过程中,噪音和外部干扰普遍存在.比如,同步信号从驱动系统传输到响应系统的工程中,外部环境中的干扰不可避免.然而,干扰的存在可能会破坏系统的稳定性与同步现象.故干扰抑制同步控制器的设计就成为一个尤为重要的问题.在干扰输入信号平方可积的情况下,L2-增益概念提供了L2扰动输入信号对输出信号灵敏度的数值度量.H∞同步控制是消除外部干扰对系统性能影响的有效方法.文献[22]得到了不确定神经网络时滞相关的H∞同步判据.文献[23]提出滑膜控制方法来研究具有混合时滞系统的H∞同步问题.文献[24]基于分布脉冲控制策略研究一类具有耦合时滞和干扰信号的复杂动态网路的在H∞同步问题.H∞同步的目的就是设计控制律(状态反馈或者输出反馈),使得闭环系统在零干扰任意初始值的情况下,系统内稳定且在零初始时系统具有有限L2-增益.混沌系统的间歇H∞同步问题未见有报道,而解决该问题的最大难点就是如何构造合适的Lyapunov函数使得系统在开环模式下具有有限的L2-增益.
本文提出非周期间歇H∞同步方案,保证误差系统指数稳定和误差干扰输出具有规定的L2-增益.对于给定的间歇切换信号,非周期间歇H∞同步控制器的增益可以通过求解一组线性矩阵不等式得到.主要创新点如下:(1)基于H∞同步理论,以量化的形式分析干扰对误差系统的影响并且考虑了间歇H∞控制设计;(2)与文献[12-19]中相比,本文中的间歇控制的控制宽度和休息宽度可变;(3)构造的时变切换的Lyapunov函数更能够考虑系统的切换特性,使得同步判据具有更小的保守性.
符号说明:矩阵P>0(≥0, < 0, ≤0)表示P为正定(半正定、负定、半负定)矩阵;I表示适当维数的单位矩阵;λmax(P), λmin(P)分别表示矩阵P的最大和最小特征值;‖·‖表示为欧几里德范数;
考虑如下常微分方程描述的非线性系统:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot x\left( t \right) = {A_0}x\left( t \right) + {A_1}f\left( {x\left( t \right)} \right),}\\ {y\left( t \right) = Cx\left( t \right),}\\ {x\left( 0 \right) = {x_0},} \end{array}} \right. $ | (1) |
其中,x(t)∈Rn,y(t)∈Rm分别是系统的状态与系统的输出;A0, A1∈Rn×n为已知的常系数矩阵;C∈Rm×n, m < n为系统的控制输出矩阵;x0∈Rn为系统的初值.f(·):Rn→Rn为非线性函数并且满足f(0)=0和如下假设:
(H1)对任意的i∈{1, 2, …, n},存在ki, ki,使得如下不等式成立:
| $ {\underline \kappa _i} \le \frac{{{f_i}\left( x \right) - {f_i}\left( y \right)}}{{x - y}} \le {{\bar \kappa }_i},x \ne y, $ | (2) |
系统(1)为驱动系统,相应的响应系统具有如下形式:
| $ \left\{ \begin{array}{*{35}{l}} \dot{\hat{x}}\left( t \right)={{A}_{0}}\hat{x}\left( t \right)+{{A}_{1}}f\left( \hat{x}\left( t \right) \right)+Bu\left( t \right)+{{D}_{1}}w\left( t \right), \\ \hat{y}\left( t \right)=C\hat{x}\left( t \right)+{{D}_{2}}w\left( t \right), \\ \hat{x}\left( 0 \right)={{{\hat{x}}}_{0}}, \\ \end{array} \right. $ | (3) |
其中,
| $ u\left( t \right) = K\left( t \right)\left( {x\left( t \right) - \hat x\left( t \right)} \right), $ | (4) |
其中,
| $ K\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {- K, t \in {\Delta _{1k}} \buildrel \Delta \over = \left[{{t_{1, k- 1}}, \left. {{t_{2, k- 1}}} \right)} \right., }\\ {0, t \in {\Delta _{2K}} \buildrel \Delta \over = \left[{{t_{2, k-1}}, \left. {{t_{1k}}} \right)} \right., } \end{array}k \in \mathbb{N}.} \right. $ |
定义同步误差:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot e\left( t \right) = \left( {{A_0} + BK} \right)e\left( t \right) + {A_1}\hat f\left( {e\left( t \right)} \right) - {D_1}w\left( t \right),t \in {\Delta _{1k}},}\\ {\dot e\left( t \right) = {A_0}e\left( t \right) + {A_1}\hat f\left( {e\left( t \right)} \right) - {D_1}w\left( t \right),t \in {\Delta _{2k}},}\\ {{y_e} = Ce\left( t \right) - {D_2}w\left( t \right),}\\ {e\left( 0 \right) = {e_0},} \end{array}} \right. $ | (5) |
其中,
| $ {\underline \kappa _i} \le \frac{{{{\hat f}_i}\left( {{e_i}} \right)}}{{{e_i}}} \le {{\bar \kappa }_i},{e_i} \ne 0,i = 1,2, \cdots ,n, $ | (6) |
与周期间歇控制相比,非周期间歇控制允许控制周期t1k-t1, k-1与控制宽度t2, k-1-t1, k-1是变化的.为了刻画系统的切换特征,引入如下切换信号函数:
| $ \sigma \left( t \right) = \left\{ {\begin{array}{*{20}{l}} {1, t \in \bigcup\limits_{t \in \mathbb{N}} {{\Delta _{1k}}}, }\\ {2, t \in \bigcup\limits_{t \in \mathbb{N}} {{\Delta _{1k}}}, } \end{array}k \in \mathbb{N}.} \right. $ |
给出间歇切换时间序列满足的容许值:
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;{S_\sigma }\left( {{\delta _{11}}, {\delta _{12}};{\delta _{21}}, {\delta _{22}}} \right) = \left\{ {\sigma \left( t \right):{\delta _{i1}} \le {t_{3-i, k + i-2}}-} \right.}\\ {\left. {{t_{i, k - 1}} \le {\delta _{i2}}, k \in \mathbb{N}, i = 1, 2} \right\}.} \end{array} $ |
间歇H∞同步问题:对于给定的干扰抑制γ和给定间歇切换时间序列Sσ(δ11, δ12; δ21, δ22), 设计间歇控制器K, 使以下条件成立:
(i)当外部干扰w(·)=0时,误差系统的零解是一致指数稳定(UES), 即存在正标量M, β,使得如下不等式成立:
‖e(t)‖2≤M‖e0‖2e-βt, ∀t≥0.
(ii)当初始值e0=0时,同步误差系统(5)的控制输出ye(t)满足
| $ \int_0^t {{{\left\| {{y_e}\left( s \right)} \right\|}^2}{\rm{d}}s \le {\gamma ^2}\int_0^t {{{\left\| {w\left( s \right)} \right\|}^2}{\rm{d}}s,} \forall t \ge 0.} $ | (7) |
引理1[17]对给定的Un×n矩阵和正定矩阵X,对任意的正常数ε,如下不等式成立:
| $ U{X^{-1}}{U^{-1}} \ge \varepsilon \left( {U + {U^T}} \right)-{\varepsilon ^2}X. $ |
引理2[17]给定的矩阵A∈Rn×n, B∈Rn×n, Ξi∈Rn×n, Ξi=ΞiT, X0, Xi, Hi∈Rn×n, i=1, 2, …, N.如果如下矩阵不等式成立:
| $ \begin{array}{*{20}{l}} {\left[{\begin{array}{*{20}{c}} {{\Xi _i} + B{X_0}A + {{\left( {B{X_0}A} \right)}^{\rm{T}}}}&{{{\left( {\left( {{X_i}-{X_0}} \right)A} \right)}^{\rm{T}}} + B{H_i}}\\ *&{-{H_i}-H_i^{\rm{T}}} \end{array}} \right] < 0, }\\ {i = 1, 2, \cdots, N, } \end{array} $ |
则下列不等式也成立:
| $ {\Xi _i} + B{X_i}A + {\left( {B{X_i}A} \right)^{\rm{T}}} < 0, i = 1, 2, \cdots, N. $ |
通过引入时变Lyapunov函数,结合凸组合技术和线性矩阵不等式技术,解决间歇H∞同步问题.首先引入相关的分段函数:
| $ \begin{array}{*{20}{l}} {{\rho _0}\left( t \right) = \frac{1}{{{t_{3-i, k + i-2}}-{t_{i, k - 1}}}}, t \in {\Delta _{ik}}, k \in \mathbb{N}, i = 1, 2, }\\ {{\rho _1}\left( t \right) = \frac{{t - {t_{i, k - 1}}}}{{{t_{3 - i, k + i - 2}} - {t_{i, k - 1}}}}, t \in {\Delta _{ik}}, k \in \mathbb{N}, i = 1, 2}\\ {{{\tilde n}_1}\left( t \right) = \frac{{{\rho _0}\left( t \right) - 1/{\delta _{i2}}}}{{1/{\delta _{i1}} - 1/{\delta _{i2}}}}, t \in {\Delta _{ik}}, k \in \mathbb{N}, i = 1, 2, } \end{array} $ |
由ρ0(t), ρ1(t),
| $ {\rho _0}\left( t \right) = \frac{{{{\tilde n}_1}\left( t \right)}}{{{\delta _{i1}}}} + \frac{{{{\tilde n}_2}\left( t \right)}}{{{\delta _{i2}}}}, t \in {\Delta _{ik}}, k \in \mathbb{N}, i = 1, 2, $ |
和
| $ {\rho _1}\left( {{t_{i,k - 1}}} \right) = 0,{\rho _1}\left( {t_{20}^ - } \right) = {\rho _1}\left( {t_{ik}^ - } \right) = 1,k \in \mathbb{N},i = 1,2, $ | (8) |
定义:
定理1给定控制增益矩阵K∈Rm×nc和间歇切换时间序列Sσ(δ11, δ12; δ21, δ22),考虑同步误差系统(5)满足(6)式.那么对于给定正标量μ1, μ2, γ,若存在n×n正定矩阵Pij, j=1, 2和正定对角矩阵λijh, i, j, h=1, 2,使得如下线性矩阵不等式成立:
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;{\Xi _{ijh}} = }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\mathit{\Omega}} _{ijh}}}&{{P_{ij}}{A_1} + {\mathit{\Lambda } _{ijh}}{L_2}}&{ - {P_{ij}}{D_1}}&{{C^{\rm{T}}}}\\ *&{ - {\mathit{\Lambda } _{ijh}}}&0&0\\ *&*&{ - {\mu _0}{\gamma ^2}I}&{ - D_2^{\rm{T}}}\\ *&*&*&{ - I} \end{array}} \right] < 0,i,j,}\\ {h = 1,2,} \end{array} $ | (9) |
| $ {P_{i2}} \le {\mu _{3 - i,1}},i = 1,2, $ | (10) |
其中,
则系统(5)关于Sσ一致指数稳定且L2-增益小于γ.
证明首先,证明当w(·)=0时,误差系统(5)在给定的条件(8)和(9)下是指数稳定的.在此,把误差系统(5)看作如下切换系统:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot e\left( t \right) = {A_{0,\sigma \left( t \right)}}e\left( t \right) + {A_1}\hat f\left( {e\left( t \right)} \right),}\\ {e\left( 0 \right) = {e_0}.} \end{array}} \right. $ | (11) |
由矩阵不等式(9),(10),对于充分小的正标量β, 条件(10)和如下不等式成立:
| $ {\Xi _{1ijh}} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\tilde \Omega} }_{ijh}}}&{{P_{ij}}{A_1} + {\mathit{\Lambda } _{ijh}}{L_2}}\\ *&{ - {\mathit{\Lambda } _{ijh}}} \end{array}} \right],i,j,h = 1,2, $ | (12) |
其中,
构造时变的Lyapunov候选函数:
| $ V\left( t \right) = \varphi \left( t \right)\sum\limits_{j = 1}^2 {e\left( t \right)} {\rho _{\sigma \left( t \right), j}}{P_{\sigma \left( t \right), j}}e\left( t \right), \varphi \left( t \right) = \mu _{\sigma \left( t \right)}^{{\rho _1}\left( t \right)}. $ |
设W(t)=eβ tV(t),对任意固定的t∈[ti, k-1, t3-i, k+i-2), (i, k)∈{1, 2}×
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\dot W\left( t \right) = {e^{\beta t}}\sum\limits_{j = 1}^2 {{\rho _j}\left( t \right)\left\{ {{e^{\rm{T}}}\left( t \right)\left[{\left. {\beta + {\rho _0}\left( t \right)\ln {\mu _i}} \right)} \right.} \right.{P_{ij}} + } }\\ {\left. {{\rho _0}\left( t \right)\left( {{P_{i1}}-{P_{i2}}} \right) + {P_{ij}}{A_{0i}} + {A_{0i}}{P_{ij}}} \right]e\left( t \right) + }\\ {\left. {2{e^{\rm{T}}}\left( t \right){P_{ij}}\hat f\left( {e\left( t \right)} \right)} \right\}} \end{array} $ |
根据不等式(6)可得
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;0 \le \left( {{{\underline \kappa }_q}{e_q}-{{\hat f}_q}\left( {{e_q}} \right)} \right)\left( {{{\bar \kappa }_q}{e_q}-{{\hat f}_q}\left( {{e_q}} \right)} \right), }\\ {q = 1, 2, \cdots, n.} \end{array} $ |
设λijh=diag{λijh1, λijh2, …, λijhn}, i, j, =1, 2.根据上面不等式得
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;0 \le {e^{\beta t}}\varphi \left( t \right)\sum\limits_{q = 1}^n {\sum\limits_{j,h = 1}^2 {{\rho _j}} \left( t \right){{\tilde n}_h}\left( t \right){\mathit{\Lambda } _{ijh}}\left( {{{\underline \kappa }_q}{e_q} - } \right.} }\\ {\left. {{{\hat f}_q}\left( {{e_q}} \right)} \right)\left( {{{\bar \kappa }_q}{e_q} - {{\hat f}_q}\left( {{e_q}} \right)} \right) = \sum\limits_{q = 1}^n {\sum\limits_{j,h = 1}^2 {{\rho _j}\left( t \right){{\tilde n}_h}\left( t \right)\left\{ {{e^{\rm{T}}}\left( t \right) \cdot } \right.} } }\\ {{\mathit{\Lambda }_{ijh}}{L_1}e\left( t \right) + {e^{\rm{T}}}\left( t \right){\mathit{\Lambda }_{ijh}}{L_2}\hat f\left( {e\left( t \right)} \right) + }\\ {\left. {{{\left( {\hat f\left( {e\left( t \right)} \right)} \right)}^{\rm{T}}}{\mathit{\Lambda }_{ijh}}\hat f\left( {e\left( t \right)} \right)} \right\}.} \end{array} $ | (13) |
把(13)式与(t)相加可得
| $ \dot W\left( t \right) \le {e^{\beta t}}\varphi \left( t \right)\sum\limits_{j, h = 1}^2 {\eta _1^{\rm{T}}\left( t \right)} {\rho _j}\left( t \right){{\tilde n}_h}\left( t \right){\Xi _{1ijh}}{\eta _1}\left( t \right), $ |
其中,
| $ \dot W\left( t \right) < 0, {\forall _t} \in \left[{{t_{i, k-1}}, \left. {{t_{3-i, k + i-2}}} \right)} \right., $ |
所以
| $ W\left( t \right) < W\left( {{t_{i,k - 1}}} \right),\forall t \in \left[ {{t_{i,k - 1}},\left. {{t_{3 - i,k + i - 2}}} \right).} \right. $ | (14) |
根据(7)式和(9)式,给出W(t)在切换时刻ti, k-1,(i, k)∈{1, 2}×
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;W\left( {{t_{i,k - 1}}} \right) = {e^{\beta {t_{i,k - 1}}}}\varphi \left( {{t_{i,k - 1}}} \right){e^{\rm{T}}}\left( {{t_{i,k - 1}}} \right) \cdot }\\ {\sum\limits_{j = 1}^2 {{\rho _j}\left( {{t_{i,k - 1}}} \right)} {P_{ij}}e\left( {{t_{i,k - 1}}} \right) = {e^{\beta {t_{i,k - 1}}}}{e^{\rm{T}}}\left( {{t_{i,k - 1}}} \right) \cdot }\\ {{P_{i2}}e\left( {{t_{i,k - 1}}} \right) \le {e^{\beta {t_{i,k - 1}}}}{\mu _{3 - i}}{e^{\rm{T}}}\left( {{t_{i,k - 1}}} \right){P_{3 - i,1}}e\left( {{t_{i,k - 1}}} \right) \le }\\ {{e^{\beta {t_{i,k - 1}}}}\mu _{3 - i}^{{\rho _1}\left( {t_{i,k - 1}^ - } \right)}{e^{\rm{T}}}\left( {{t_{i,k - 1}}} \right){P_{3 - i,1}}e\left( {{t_{i,k - 1}}} \right) = }\\ {{e^{\beta {t_{i,k - 1}}}}\mu _{3 - i}^{{\rho _1}\left( {t_{i,k - 1}^ - } \right)}{e^{\rm{T}}}\left( {{t_{i,k - 1}}} \right){P_{3 - i,1}}e\left( {t_{i,k - 1}^ - } \right) = W\left( {t_{i,k - 1}^ - } \right).} \end{array} $ | (15) |
结合(14)式和(15)式,得W(t)≤W(0).可以推出
| $ \left\| {e\left( t \right)} \right\| \le \sqrt {\frac{{{\lambda _2}}}{{{\lambda _1}\min \left\{ {{\mu _1}, {\mu _2}, 1} \right\}}}} \left\| {{e_0}} \right\|{e^{\frac{{-\beta t}}{2}}}, $ |
其中,λ2=λmax (P12), λ1=min {λmin(Pij), i, j=1, 2}.因此同步误差系统(11)关于Sσ(δ11, δ12; δ21, δ22)是一致指数稳定的.
接下来证明, 当初始值e(0)=0时,控制输出ye(t)满足不等式(7).为此,引入辅助函数:
| $ J\left( t \right) = \int_0^t {\varphi \left( s \right)\left( {{{\left\| {{y_e}\left( s \right)} \right\|}^2}-{\mu _0}{\gamma ^2}{{\left\| {w\left( s \right)} \right\|}^2}} \right)} {\rm{d}}s, t \ge 0. $ |
对任意的s≥0,存在k∈
| $ .\begin{array}{*{20}{l}} {\;\;\;\;\;\int_0^t {\dot V\left( s \right){\rm{d}}s = \sum\limits_{l = 0}^{k-1} {\left( {\int_{{t_{1l}}}^{{t_{2l}}} + \int_{{t_{1l}}}^{{t_1}, l + 1} {\dot V\left( s \right)} {\rm{d}}s} \right)} + } }\\ {\int_{{t_{1k}}}^t {\dot V\left( s \right){\rm{d}}s} = \sum\limits_{l = 0}^{k-1} {\left( {V\left( {t_{2l}^-} \right) - V\left( {{t_{il}}} \right) + V\left( {t_{1, l + 1}^ - } \right) - } \right.} }\\ {\left. {V\left( {{t_{2l}}} \right)} \right) + V\left( t \right) - V\left( {{t_{1k}}} \right) \ge \sum\limits_{l = 0}^{k - 1} {\left( {V\left( {t_{2l}^ - } \right) - V\left( {{t_{2l}}} \right)} \right) + } }\\ {\sum\limits_{l = 1}^k {\left( {V\left( {t_{1, l + 1}^ - } \right) - V\left( {{t_{1l}}} \right)} \right)} \ge 0.} \end{array} $ |
那么,如下不等式成立:
| $ \begin{array}{*{20}{l}} {\;\;\;\;J\left( t \right) = \int_0^t {\varphi \left( s \right)\left( {{{\left\| {{y_e}\left( s \right)} \right\|}^2} - {\mu _0}{\gamma ^2}{{\left\| {w\left( s \right)} \right\|}^2}} \right) + } }\\ {\dot V\left( s \right){\rm{d}}s - \int_0^t {\dot V\left( s \right){\rm{d}}s} \le \int_0^t {\varphi \left( s \right)} \left( {{{\left\| {{y_e}\left( s \right)} \right\|}^2} - } \right.}\\ {\left. {{\mu _0}{\gamma ^2}{{\left\| {w\left( s \right)} \right\|}^2} + \dot V\left( s \right)} \right){\rm{d}}s.} \end{array} $ | (16) |
对任意的s∈[ti, k-1, t3-i, k+i-2), (i, k)∈{1, 2}×
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\varphi \left( s \right)\left( {{{\left\| {{y_e}\left( s \right)} \right\|}^2}- {\mu _0}{\gamma ^2}{{\left\| {w\left( s \right)} \right\|}^2} + \dot V\left( s \right)} \right. = }\\ {\varphi \left( s \right)\sum\limits_{j = 1}^2 {{\rho _j}} \left( s \right)\left\{ {{e^{\rm{T}}}\left( s \right)\left[{{\rho _0}\left( t \right)\ln {\mu _i}} \right.} \right.{P_{ij}} + {\rho _0}\left( t \right)\left( {{P_{i2}}-} \right.}\\ {\left. {\left. {{P_{i1}}} \right) + {P_{ij}}{A_{0i}} + {A_{0i}}{P_{ij}}} \right]e\left( s \right) + 2{e^{\rm{T}}}\left( s \right){P_{ij}}{A_1}\hat f\left( {e\left( s \right)} \right) -}\\ {\left. {2{e^{\rm{T}}}\left( s \right){P_{ij}}{D_1}w\left( s \right) + y_e^{\rm{T}}\left( s \right) -{\mu _0}{\gamma ^2}{w^{\rm{T}}}\left( s \right)w\left( s \right)} \right\}.} \end{array} $ |
再结合不等式(13)和上式有
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\varphi \left( s \right)\left( {{{\left\| {{y_e}\left( s \right)} \right\|}^2}-{\mu _0}{\gamma ^2}{{\left\| {w\left( s \right)} \right\|}^2} + \dot V\left( s \right)} \right. \le }\\ {\varphi \left( s \right)\sum\limits_{j, h = 1}^2 {{\rho _j}} \left( s \right){{\tilde n}_h}\left( s \right)\eta _2^{\rm{T}}\left( s \right)\left( {{\Xi _{2ijh}} + {H^{\rm{T}}}H} \right){\eta _2}\left( s \right), } \end{array} $ |
其中sη2(s)=col(η1(s), w(s)), H=[C 0 -D2],
| $ {\Xi _{2ijh}} = \left[{\begin{array}{*{20}{c}} {{\mathit{\Omega} _{ijh}}}&{{P_{ij}}{A_1} + {\mathit{\Lambda }_{ij}}{L_2}}&{-{P_{ij}}{D_1}}\\ *&{-{\Lambda _{ijh}}}&0\\ *&*&{-{\mu _0}{\gamma ^2}I} \end{array}} \right]. $ |
根据不等式(9),应用Schur补引理可以得到
Ξ2ijh+HTH < 0.
因此
| $ \varphi \left( s \right)\left( {{{\left\| {{y_e}\left( s \right)} \right\|}^2}-{\mu _0}{\gamma ^2}{{\left\| {w\left( s \right)} \right\|}^2} + \dot V\left( s \right)} \right. < 0. $ |
把上式代入(16)式,推出J(t)≤0, ∀t≥0, 即
| $ \int_0^1 {\varphi \left( s \right){{\left\| {{y_e}\left( s \right)} \right\|}^2}{\rm{d}}s} \le \int_0^1 {{\mu _0}{\gamma ^2}\varphi \left( s \right)} {\left\| {w\left( s \right)} \right\|^2}{\rm{d}}s, \\ \forall t \ge 0. $ |
由于min {μ1, μ2, 1}≤φ(s)≤max {μ1, μ2, 1}, 就意味着不等式(5)成立.证毕.
假设间歇切换时间序列Sσ(δ11, δ12; δ21, δ22)满足δ11=δ12, δ21=δ22, 则非周期间歇控制就成为周期间歇控制,那么根据定理1可得如下推论.
推论1给定控制增益矩阵K∈Rm×nc,控制周期ω和控制宽度δ,考虑同步误差系统(5)满足(6)式.对于给定正标量μ1, μ2, γ,若存在n×n正定矩阵Pij, i, j=1, 2和正定对角矩阵λij, i, j=1, 2,使得如下线性矩阵不等式成立:
| $ \begin{array}{*{20}{l}} {\;\;\;\;{\Xi _{ij}} = \left[{\begin{array}{*{20}{c}} {{\mathit{\Omega} _{ij}}}&{{P_{ij}}{A_1} + {\mathit{\Lambda }_{ij}}{L_2}}&{-{P_{ij}}{D_1}}&{{C^{\rm{T}}}}\\ *&{-{\mathit{\Lambda }_{ij}}}&0&0\\ *&*&{-{\mu _0}{\gamma ^2}I}&{ - D_2^{\rm{T}}}\\ *&*&*&{ - I} \end{array}} \right] < }\\ {0, i, j = 1, 2, }\\ {\;\;\;\;\;{P_{i2}} \le {\mu _{3 -i}}{P_{3 -i, 1}}, i = 1, 2, } \end{array} $ |
其中
则系统(5)全局指数稳定且L2-增益小于γ.
注1文献[11-16]研究了系统的周期间歇同步问题.然而在实际中,周期间歇控制是不合理或者没必要的.与之前文献不同,本文所提出的间歇控制的控制窗口宽度和休息宽度是可变的.另外,定理1提出了新颖的时变切换Lyapunov函数来研究系统的H∞同步问题.时变切换Lyapunov函数能够使系统在开环模式上具有有限L2-增益.传统的时不变Lyapunov函数在分析L2-增益时,即使γ充分大,也不能满足不等式:
| $ {\left\| {{y_e}\left( s \right)} \right\|^2}-{\gamma ^2}{\left\| {w\left( s \right)} \right\|^2} + \dot V\left( s \right) \le 0. $ |
说明本文提出的时变Lyapunov函数更具优越性.
3 控制器设计在定理1的基础上解决间歇H∞同步控制器的设计问题.给出如下假设:
(H2)假设(H1)成立,且κi, κi, i=1, 2, …, n满足如下条件:
| $ {\underline \kappa _i} \le 0 \le {{\bar \kappa }_i}. $ |
定理2给定间歇切换时间序列Sσ(δ11, δ12; δ21, δ22), 考虑驱动系统(1)满足假设(H1),间歇受控响应系统(3)和间歇控制律(4).对于给定正标量μi, εi, θi, γ, i=1, 2,若存在n×n正定矩阵Xij, i, j=1, 2, 正定对角矩阵λijh, i, j, h=1, 2和n×n可逆矩阵x0, m×nc矩阵, 使得如下线性矩阵不等式成立:
| $ {X_{3 - i,1}} \le {\mu _{3 - i}}{X_{i2}},i = 1,2, $ | (17) |
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\Gamma} _{11h}}}&{I_0^{\rm{T}}\left( {{X_{11}} - X_0^{\rm{T}} + {\theta _1}B\bar K} \right)}\\ *&{ - {\theta _1}\left( {{X_0} + X_0^{\rm{T}}} \right)} \end{array}} \right] < 0,h = 1,2, $ | (18) |
| $ \begin{array}{*{35}{l}} \ \ \ \ \ \ \ \left[ \begin{matrix} {{\mathit{\Gamma }}_{12h}} & {{X}_{12}} & I_{0}^{\text{T}}\left( {{X}_{12}}-X_{0}^{\text{T}}+{{\theta }_{2}}B\bar{K} \right) \\ * & -{{\delta }_{1h}}{{X}_{11}} & 0 \\ * & * & -{{\theta }_{2}}\left( {{X}_{}}_{0}+X_{0}^{\text{T}} \right) \\ \end{matrix} \right] < 0, \\ h=1,2, \\ \end{array} $ | (19) |
| $ {\mathit{\Gamma }_{21h}} < 0,h = 1,2, $ | (20) |
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\Gamma} _{22h}}}&{{X_{22}}}\\ *&{ - {\delta _{2h}}{X_{21}}} \end{array}} \right] < 0,h = 1,2, $ | (21) |
其中,
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;{\mathit{\Gamma} _{ijh}} = }\\ {\left[{\begin{array}{*{20}{c}} {{\mathit{\Psi }_{ijh}}}&{{A_1}{{\mathit{\bar \Lambda }}_{ijh}} + {X_{ij}}{L_2}}&{-{D_1}}&{{X_{ij}}{C^{\rm{T}}}}&{{X_{ij}}\bar L_1^{\rm{T}}}\\ *&{-{{\mathit{\bar \Lambda }}_{ijh}}}&0&0&0\\ *&*&{-{\mu _0}{\gamma ^2}I}&{ - D_2^{\rm{T}}}&0\\ *&*&*&{ - I}&0\\ *&*&*&*&{ - {{\mathit{\mathit{\bar \Lambda }}}_{ijh}}} \end{array}} \right], }\\ {i, j, h = 1, 2, } \end{array} $ |
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;{\mathit{\Psi }_{11h}} = \frac{{\ln {\mu _1} + 1-2{\varepsilon _1}}}{{{\delta _{1h}}}}{X_{11}} + \frac{{\varepsilon _1^2}}{{{\delta _{1h}}}}{X_{12}} + {A_0}{X_{11}} + }\\ {{X_{11}}A_0^{\rm{T}} + B\bar K + {{\bar K}^{\rm{T}}}{B^{\rm{T}}}, {\mathit{\Psi }_{12h}} = \frac{{\ln {\mu _1}-1}}{{{\delta _{1h}}}}{X_{12}} + {A_0}{X_{12}} + }\\ {{X_{12}}A_0^{\rm{T}} + B\bar K + {{\bar K}^{\rm{T}}}{B^{\rm{T}}}, {\mathit{\Psi }_{21h}} = \frac{{\ln {\mu _2} + 1-2{\varepsilon _2}}}{{{\delta _{2h}}}}{X_{21}} + }\\ {\frac{{\varepsilon _2^2}}{{{\delta _{2h}}}}{X_{22}} + {A_0}{X_{21}} + {X_{21}}A_0^{\rm{T}}, {\mathit{\Psi }_{22h}} = \frac{{\ln {\mu _2}}}{{{\delta _{2h}}}}{X_{22}} + }\\ {{A_0}{X_{22}} + {X_{22}}A_0^{\rm{T}}.} \end{array} $ |
则K=KX0-1,那么驱动系统(1)和响应系统(3)关于Sσ(δ11, δ12; δ21, δ22)一致指数稳定且L2-增益小于γ.
证明令Xij=Pij-1, K=KX0-1,
| $ -{X_{11}}X_{12}^{-1}{X_{11}} \le-2{\varepsilon _1}{X_{11}} + \varepsilon _1^2{X_{12}}. $ |
利用Schur补引理以及上式不等式,由线性矩阵不等式(18)和(19)可得
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{{\mathit{\tilde \Gamma} }_{1jh}} - {B_1}{X_0}A - {{\left( {{B_1}{X_0}A} \right)}^{\rm{T}}}}&{{A^{\rm{T}}}\left( {{X_{1j}} - X_0^{\rm{T}}} \right) + {B_1}\left( {{\theta _j}{X_0}} \right)}\\ *&{ - {\theta _j}\left( {{X_0} + X_0^{\rm{T}}} \right)} \end{array}} \right] < 0,}\\ {j = 1,2,} \end{array} $ | (22) |
其中,A=[I 0 0 0], B1=col(BK, 0, 0, 0),
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;\;{{\mathit{\tilde \Gamma }}_{1jh}} = }\\ {\left[{\begin{array}{*{20}{c}} {{{\mathit{\tilde \Psi }}_{1jh}}}&{{A_1}{{\mathit{\bar \Lambda }}_{1jh}} + {X_{1j}}{L_2}}&{-{D_1}}&{{X_{1j}}{C^{\rm{T}}}}\\ *&{-{{\mathit{\bar \Lambda }}_{1jh}}}&0&0\\ *&*&{-{\mu _0}{\gamma ^2}I}&{ - D_2^{\rm{T}}}\\ *&*&*&{ - I} \end{array}} \right], }\\ {{{\mathit{\tilde \Psi }}_{1jh}} = \frac{{\ln {\mu _1}}}{{{\delta _{1h}}}}{X_{1j}} + \frac{{\ln {\mu _1}}}{{{\delta _{1h}}}}{X_{1j}}\left( {{P_{11}} -{P_{12}}} \right){X_{1j}} + {A_0}{X_{1j}} + }\\ {{X_{1j}}A_0^{\rm{T}} + {X_{1j}}{\mathit{\Lambda }_{1jh}}{L_1}{X_{1j}}.} \end{array} $ |
根据引理2,由矩阵不等式(22)可以得到
| $ {{\mathit{\tilde \Gamma }}_{1jh}} - {B_1}{X_{1j}}A - {\left( {{B_1}XA} \right)^{\rm{T}}} < 0,j = 1,2. $ | (23) |
在不等式两边同时乘以diag{Pij, ∧1jh, I, I},那么线性矩阵不等式(18),(19)等价于当i=1, j, h=1, 2时的线性矩阵不等式(9).利用相同的分析技巧可得线性矩阵不等式(20),(21)等价于i=2, j, h=1, 2时的线性矩阵不等式(9).再根据定理1可得结论成立.
推论2对控制周期ω和控制宽度δ,考虑驱动系统(1)满足假设(H1),间歇受控响应系统(3)和间歇控制律(4).对于给定正标量μi, εi, θi, γ, i=1, 2,若存在n×n正定矩阵Xij, i, j=1, 2, 正定对角矩阵λij, i, j=1, 2和n×n可逆矩阵x0,m×nc矩阵,使得如下线性矩阵不等式成立:
| $ \begin{array}{*{20}{l}} {{X_{3- i, 1}} \le {\mu _{3- i}}{X_{i2}}, i = 1, 2, }\\ {\left[{\begin{array}{*{20}{c}} {{\mathit{\Gamma} _{11}}}&{I_0^{\rm{T}}\left( {{X_{11}}-X_0^{\rm{T}} + {\theta _1}B\bar K} \right)}\\ *&{-{\theta _1}\left( {{X_0} + X_0^{\rm{T}}} \right)} \end{array}} \right] < 0, }\\ {\left[{\begin{array}{*{20}{c}} {{\mathit{\Gamma} _{12}}}&{{X_{12}}}&{I_0^{\rm{T}}\left( {{X_{12}}-X_0^{\rm{T}} + {\theta _2}B\bar K} \right)}\\ *&{-\delta {X_{11}}}&0\\ *&*&{-{\theta _2}\left( {{X_0} + X_0^{\rm{T}}} \right)} \end{array}} \right] < 0, }\\ {{\mathit{\Gamma} _{21}} < 0, }\\ {\left[{\begin{array}{*{20}{c}} {{\mathit{\Gamma} _{22}}}&{{X_{22}}}\\ *&{-\left( {\omega-\delta } \right){X_{21}}} \end{array}} \right] < 0, } \end{array} $ |
其中I0=[I 0 0 0 0],L-1=L11/2,
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;\;{\mathit{\Gamma }_{ij}} = }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\Psi }_{ij}}}&{{A_1}{{\mathit{\bar \Lambda }}_{ij}} + {X_{ij}}{L_2}}&{ - {D_1}}&{{X_{ij}}{C^{\rm{T}}}}&{{X_{ij}}\bar L_1^{\rm{T}}}\\ *&{ - {{\mathit{\bar \Lambda }}_{ij}}}&0&0&0\\ *&*&{ - {\mu _0}{\gamma ^2}I}&{ - D_2^{\rm{T}}}&0\\ *&*&*&{ - I}&0\\ *&*&*&*&{ - {{\mathit{\bar \Lambda }}_{ij}}} \end{array}} \right],i,j = 1,2,} \end{array} $ |
| $ \begin{array}{*{20}{l}} {{\mathit{\Psi }_{11}} = \frac{{\ln {\mu _1} + 1 - 2{\varepsilon _1}}}{\delta }{X_{11}} + \frac{{\varepsilon _1^2}}{\delta }{X_{12}} + {A_0}{X_{11}} + {X_{11}}A_0^{\rm{T}} + }\\ {B\bar K + {{\bar K}^{\rm{T}}}{B^{\rm{T}}},{\mathit{\Psi }_{12}} = \frac{{\ln {\mu _1} - 1}}{\delta }{X_{ < 12}} + {A_0}{X_{12}} + {X_{12}}A_0^{\rm{T}} + }\\ {B\bar K + {{\bar K}^{\rm{T}}}{B^{\rm{T}}},{\mathit{\Psi }_{21}} = \frac{{\ln {\mu _2} + 1 - 2{\varepsilon _2}}}{{\omega - \delta }}{X_{21}} + \frac{{\varepsilon _2^2}}{{\omega - \delta }}{X_{22}} + }\\ {{A_0}{X_{22}} + {X_{21}}A_0^{\rm{T}},} \end{array} $ |
| $ {\mathit{\Psi }_{22}} = \frac{{\ln {\mu _2}}}{{\omega-\delta }}{X_{22}} + {A_0}{X_{22}} + {X_{22}}A_0^{\rm{T}}. $ |
则K=KX0-1,驱动系统(1)和响应系统(3)完全同步且L2-增益小于γ.
注2定理2给出间歇H∞同步控制器的充分条件.而从实际出发,需尽可能使得间歇H∞同步控制器具有较小的增益.根据定理2,提出如下凸优化问题来限制增益矩阵K的范数.
(OP) minimize υ
| $ {\rm{Subject}}\;{\rm{to}}\left[ {\begin{array}{*{20}{c}} { - {X_0}}&{{{\bar K}^{\rm{T}}}}\\ *&{ - \eta {v^2}} \end{array}} \right] < 0, $ | (24) |
x0≥ηI, 线性矩阵不等式(17)-(21).
4 数值仿真考虑Chua’s电路系统,参数如下:
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;{A_0} = \left[{\begin{array}{*{20}{c}} {-\alpha b}&\alpha &0\\ 1&{-1}&1\\ 0&{-\beta }&0 \end{array}} \right], {A_1} = }\\ {\left[{\begin{array}{*{20}{c}} {-\alpha \left( {a-b} \right)}&0&0\\ 0&0&0\\ 0&0&0 \end{array}} \right], B = \left[{\begin{array}{*{20}{c}} 1\\ 0\\ 0 \end{array}} \right], C = \left[{\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right], }\\ {f\left( x \right) = \frac{1}{2}\left( {\left| {x + 1} \right.} \right) -\left. {\left| {x -1} \right|} \right), } \end{array} $ |
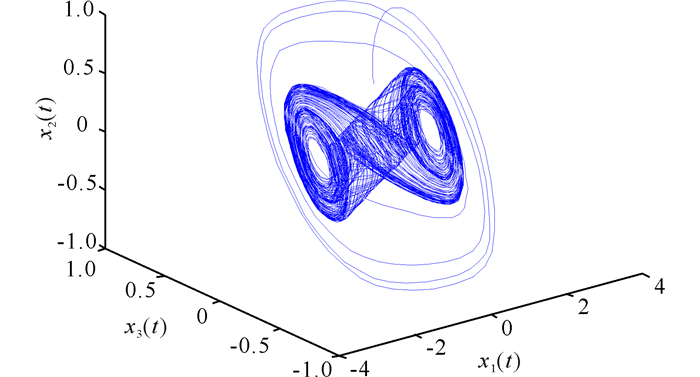
其中,α=9.215 6, β=15.994 6, a=-1.249 5, b=0.757 35.响应系统(3)具有相同的参数,并且D1=[0.1 0.1 0.1]T, D2=0.1.容易验证假设(H1)和(H2)成立,且L-1=L11/2=0.图 1展示了驱动系统的混沌现象.
|
图 1 Chua’s电路的混沌现象 Fig.1 Chaotic phenomenon of Chua's circuit system |
对于给定的δ11=0.45, δ12=0.60, δ21=0.15, δ22=0.25, 给定的L2-增益γ=1, 求解优化问题(OP).选择参数
(μ1, μ2, ε1, ε2, θ1, θ2)=(1.45, 0.29, 0.83, 0.78, 0.027, 0.032),
可得υmin =79.50.相应的间歇增益矩阵为
K=[-21.6440 -39.2940 -6.6.31].
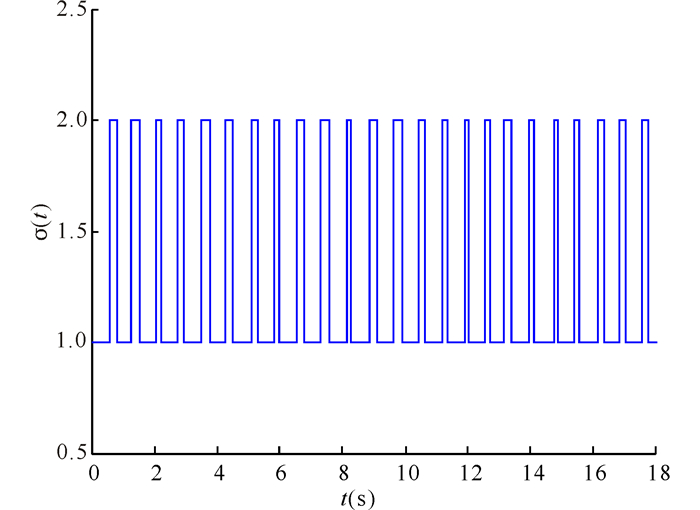
在δi1≤t3-i, k+i-2-ti, k-1≤δi2, k∈
|
图 2 间歇切换信号 Fig.2 The intermittent switching signal |
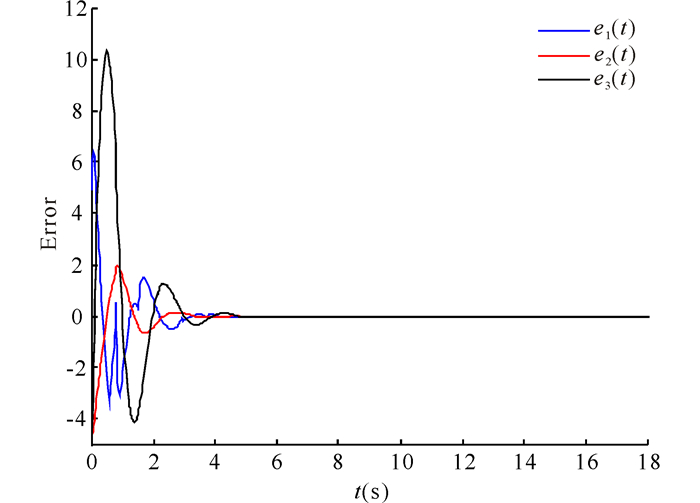
|
图 3 间歇控制下误差系统状态轨线 Fig.3 The state trajectories of error system with the intermittent control |

|
图 4 间歇控制下误差系统状态范数演化曲线 Fig.4 The state norm evolution curve of error system with the intermittent control |
本文主要研究一类非线性系统的非周期间歇H∞同步问题。通过构造切换时变的Lyapunov函数分析系统的内指数稳定性和L2-增益性能。与以往的Lyapunov函数相比,本文所提出的Lyapunov函数能够使其在开环模式上单调递减。另外,基于线性矩阵不等式,给出非周期间歇控制器的设计方案,还用数值算例验证所提结果的有效性。
| [1] |
LIU F, REN Y, SHAN X M, et al. A linear feedback synchronization theorem for a class of chaotic systems[J]. Chaos, Solitons & Fractals, 2002, 13(4): 723-730. |
| [2] |
HUANG L L, FENG R P, WANG M. Synchronization of chaotic systems via nonlinear control[J]. Physics Letters A, 2004, 320(4): 271-275. DOI:10.1016/j.physleta.2003.11.027 |
| [3] |
沈艳军, 胡俊波. 一类非线性系统连续非光滑自适应观测器设计[J]. 广西科学, 2015, 22(4): 421-424. SHEN Y J, HU J B. Continuous but nonsmooth adaptive observer design for a class of nonlinear systems[J]. Guangxi Sciences, 2015, 22(4): 421-424. |
| [4] |
TAN X H, ZHANG J Y, YANG Y R. Synchronizing chaotic systems using backstepping design[J]. Chaos, Solitons & Fractals, 2003, 16(1): 37-45. |
| [5] |
YAU H T. Design of adaptive sliding mode controller for chaos synchronization with uncertainties[J]. Chaos, Solitons & Fractals, 2004, 22(2): 341-347. |
| [6] |
CHEN W H, LU X M, ZHENG W X. Impulsive stabilization and impulsive synchronization of discrete-time delayed neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(4): 734-748. DOI:10.1109/TNNLS.2014.2322499 |
| [7] |
CHEN W H, LUO S X, ZHENG W X. Impulsive synchronization of reaction-diffusion neural networks with mixed delays and its application to image encryption[J]. IEEE Transaction on Neural Networks and Learning Systems, 2016, 31(1): 1-15. |
| [8] |
LI X D, RAKKIYAPPAN R. Impulsive controller design for exponential synchronization of chaotic neural networks with mixed delays[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(6): 1515-1523. DOI:10.1016/j.cnsns.2012.08.032 |
| [9] |
MATHIYALAGAN K, PARK J H, SAKTHIVEL R. Synchronization for delayed memristive BAM neural networks using impulsive control with random nonlinearities[J]. Applied Mathematics and Computation, 2015, 259: 967-979. DOI:10.1016/j.amc.2015.03.022 |
| [10] |
CHEN W H, JIANG Z Y, ZHONG J C, et al. On designing decentralized impulsive controllers for synchronization of complex dynamical networks with nonidentical nodes and coupling delays[J]. Journal of the Franklin Institute, 2014, 351(8): 4084-4110. DOI:10.1016/j.jfranklin.2014.04.014 |
| [11] |
YU J, HU C, JIANG H J, et al. Synchronization of nonlinear systems with delays via periodically nonlinear intermittent control[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(7): 2978-2989. DOI:10.1016/j.cnsns.2011.11.028 |
| [12] |
LI N, CAO J D. Periodically intermittent control on robust exponential synchronization for switched interval coupled networks[J]. Neurocomputing, 2014, 131: 52-58. DOI:10.1016/j.neucom.2013.10.040 |
| [13] |
ZHANG G D, SHEN Y. Exponential synchronization of delayed memristor-based chaotic neural networks via periodically intermittent control[J]. Neural Networks, 2014, 55: 1-10. DOI:10.1016/j.neunet.2014.03.009 |
| [14] |
GAN Q T. Exponential synchronization of stochastic Cohen-Grossberg neural networks with mixed time-varying delays and reaction-diffusion via periodically intermittent control[J]. Neural Networks, 2012, 31: 12-21. DOI:10.1016/j.neunet.2012.02.039 |
| [15] |
CHEN W H, ZHONG J C, JIANG Z Y, et al. Periodically intermittent stabilization of delayed neural networks based on piecewise Lyapunov functions/functionals[J]. Circuits, Systems, and Signal processing, 2014, 33(12): 3757-3782. DOI:10.1007/s00034-014-9827-0 |
| [16] |
蒋燕, 刘琼. 线性时滞中立型系统的周期间歇镇定[J]. 广西科学, 2015, 22(4): 438-444. JIANG Y, LIU Q. Periodically intermittent stabilization of linear neutral-type systems with delay[J]. Guangxi Sciences, 2015, 22(4): 438-444. |
| [17] |
陈武华, 钟佳成, 蒋志勇. 一类非线性系统的周期间歇镇定[J]. 广西大学学报:自然科学版, 2014, 39(2): 378-386. CHEN W H, ZHONG J C, JIANG Z Y. Stabilization of a class of nonlinear systems by using periodic intermittent control[J]. Journal of Guangxi University:Natural Science Edition, 2014, 39(2): 378-386. |
| [18] |
YANG X S, CAO J D. Stochastic synchronization of coupled neural networks with intermittent control[J]. Physics Letters A, 2009, 373(36): 3259-3272. DOI:10.1016/j.physleta.2009.07.013 |
| [19] |
黄敢基, 罗世贤, 钟佳成. 线性系统的间歇观测器设计[J]. 广西科学, 2015, 22(4): 425-429. HUNG G J, LUO S X, ZHONG J C. Intermittent observer design for linear systems[J]. Guangxi Sciences, 2015, 22(4): 425-429. |
| [20] |
LIU X W, CHEN T P. Synchronization of nonlinear coupled networks via aperiodically intermittent pinning control[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(1): 113-126. DOI:10.1109/TNNLS.2014.2311838 |
| [21] |
SONG Q K, HUANG T W. Stabilization and synchronization of chaotic systems with mixed time-varying delays via intermittent control with non-fixed both control period and control width[J]. Neurocomputing, 2015, 154: 61-69. DOI:10.1016/j.neucom.2014.12.019 |
| [22] |
KARIMI H R, GAO H J. New delay-dependent exponential H∞ synchronization for uncertain neural networks with mixed time delays[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2010, 40(1): 173-185. DOI:10.1109/TSMCB.2009.2024408 |
| [23] |
KARIMI H R. A sliding mode approach to H∞ syn-chronization of master-slave time-delay systems with Markovian jumping parameters and nonlinear uncertainties[J]. Journal of the Franklin Institute, 2012, 349(4): 1480-1496. DOI:10.1016/j.jfranklin.2011.09.015 |
| [24] |
CHEN W H, JIANG Z Y, LU X M, et al. H∞ synchronization for complex dynamical networks with coupling delays using distributed impulsive control[J]. Nonlinear Analysis: Hybrid Systems, 2015, 17: 111-127. DOI:10.1016/j.nahs.2015.02.004 |
 2016, Vol. 23
2016, Vol. 23 


